基于超椭球贝叶斯网络的配电系统可靠性评估

葛轶，周步祥

（四川大学 电气信息学院，成都 610065）

0 引 言

配电系统作为电力系统向用户供电的终端环节，其运行可靠性在很大程度上直接影响了整个电力系统的供电可靠性［1］。因此，一个有效的配电系统可靠性评估方法对于优化配电系统运行方式，进而增强整个电力系统的供电安全具有重要的意义［2］。截至目前，国内外有大量学者对配电系统可靠性评估领域进行了研究。文献［3］应用手动块层级结构和自动块层级结构以得到负荷点故障持续时间和故障率，进而对配电系统进行可靠性评估；文献［4］应用改进威布尔分布和对数正态分布以得到元件寿命周期和修复时间，进而对配电系统进行可靠性评估。上述文献从不同角度对配电系统可靠性评估进行了分析，但并没有对配电系统实际运行中元件故障概率无法以精确值描述的问题进行充分的考虑。

贝叶斯网络（Bayesian Network，BN）是一种对有限离散随机变量间概率关系的图解描述，在评估系统可靠性和辨识系统薄弱环节等方面得到了广泛应用［5-7，16-19］。由于实际系统元件故障概率无法以精确值描述，有学者将区间模型与贝叶斯网络相结合，产生了区间贝叶斯网络法［8］。文献［9］应用区间数以得到逻辑门区间算子，进而对系统进行可靠性评估。区间模型对于统计数据样本较少的系统可靠性评估具有较强的适应性，但该模型所得结论过于保守，精确度不高。

超椭球模型（Hyper-ellipsoidal Model，HM）是一种凸集模型［20］，具有参数变化连续、模型结构简单和易于进行相关性分析的优点，可以较好地弥补区间模型结论过于保守的不足，更加符合实际系统可靠性评估的要求［10-13］。文献［14］应用超椭球模型以得到随机变量区间概率，进而对系统进行可靠性评估。

基于上述几方面的考虑，本文提出了一种将超椭球模型约束的元件故障区间概率与贝叶斯网络相结合的配电系统可靠性评估新方法：应用证据理论获取元件初始故障区间概率；应用超椭球模型获取贝叶斯网络分析中根节点区间概率；应用贝叶斯网络推理获取配电系统的可靠性评估指标并辨识系统薄弱环节。通过对IEEE-RBTSBus 6母线系统进行算例分析，证明了该方法适用于实际配电系统的可靠性评估。

1 贝叶斯网络和超椭球模型

1.1 贝叶斯网络

贝叶斯网络是一种对有限离散随机变量间概率关系的图解描述。描述随机变量集合X={X1，X2，…，Xn}的贝叶斯网络可抽象为二元组B={G，P}={{V，E}，P}。其中，G代表有向无环图，由节点V和节点间的有向边E组成。节点Vi表示随机变量Xi（i=1，2，…，n），有向边E表示节点间的条件依赖关系。P代表条件概率表，由随机变量间条件概率参数组成。贝叶斯网络的联合概率分布P（X）为：

式中Pa（Xi）为节点Xi的父节点集。当Pa（Xi）为空集时，P（Xi|Pa（Xi））为节点Xi先验概率P（Xi）。

1.2 超椭球模型

超椭球模型是一种根据标准化向量空间下随机变量等效单位超球坐标原点与结构失效面之间的距离来反映其偏离程度的方法。

若随机变量集合X中随机变量=1，2，…，n），其中分别为Xi的取值下界和上界。则随机变量集合X的超椭球模型描述为：

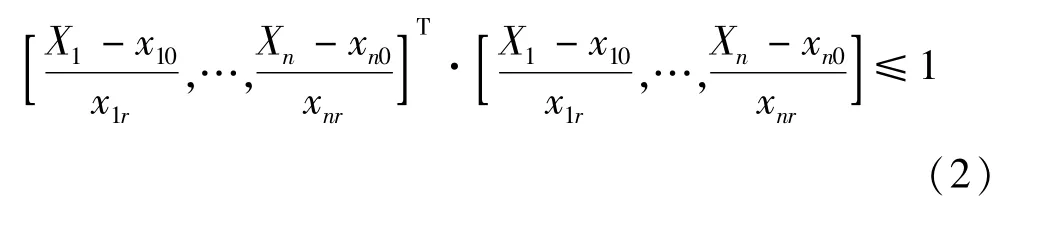
2 基于超椭球贝叶斯网络的配电系统可靠性评估

为不失一般性，选取某配电系统某负荷点LP构造贝叶斯网络，如图1所示。其中，根节点Xi（i=1，2，…n）表示与该负荷点相关的各元件Ei（i=1，2，…n）出现故障，故障概率由区间概率P（Xi）描述；叶节点XLP表示该负荷点LP出现故障，故障概率由区间概率P（XLP）描述。下面以该负荷点为例，给出基于超椭球贝叶斯网络的配电系统可靠性评估方法。

图1 某配电系统负荷点贝叶斯网络Fig.1 Bayesian network of one load point in distribution system

2.1 元件初始故障区间概率的获取

证据理论是一种通过量化命题似然率和可靠性来进行概率推理的方法。本文应用证据理论获取元件初始故障区间概率。

描述与负荷点相关的元件集合E={E1，E2，…，En}的函数mi=2E→［0，1］在满足条件：

此时为元件Ei（i=1，2，…，n）关于第i个证据的基本信度分配函数。

基本信度分配函数mp和mq的组合公式为：

由此可得元件Ei关于合成证据的信度函数Bel（Ei）和似真函数Pl（Ei）分别为：

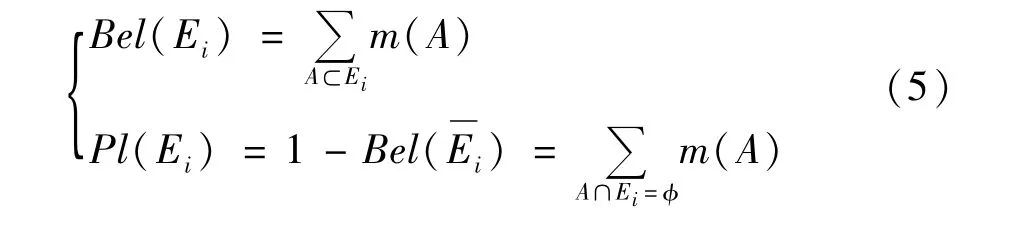
信度函数和似真函数可以较好的反映元件发生故障的概率，因此本文将信任区间［Bel（Ei），Pl（Ei）］作为元件初始故障区间概率Pin（Ei）。

2.2 贝叶斯网络根节点区间概率的获取

本文应用超椭球模型对由证据理论获取的元件初始故障区间概率Pin（Ei）进行约束，以得到可以用于贝叶斯网络分析中的根节点区间概率P（Xi）。

由式（2）可得，根节点Xi区间概率P（Xi）的超椭球模型为：

引入矢量：

式中：

则式（7）转化为：

式中：

由式（9）可得，根节点区间概率P（Xi）应在空间超椭球内部Δz=z-z0中均匀取值。设单位超椭球坐标为（r，θ1，θ2，…，θn-1），其中，r∈［0，1］，θi∈［0，2π］，则：

由式（7）～式（11）可得，根节点区间概率P（Xi）为：

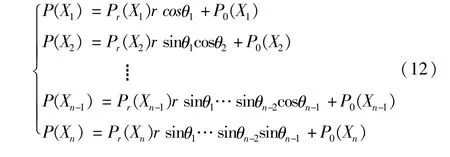
2.3 配电系统可靠性评估指标的推算

2.3.1 负荷点可靠性指标推算

应用贝叶斯网络概率推理可得叶节点XLP区间概率P（XLP）为：

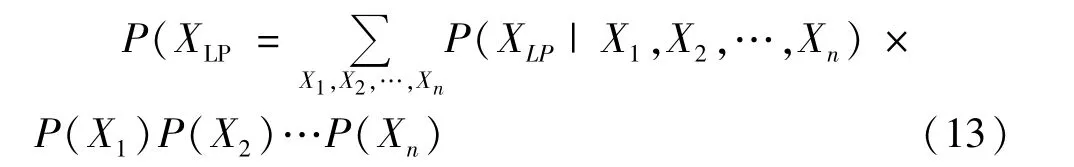
根节点区间概率P（Xi）和叶节点区间概率P（XLP）分别为超椭球模型约束下元件Ei和负荷点LP的故障区间概率。

若元件Em为线路元件，则其正常工作的区间概率为：

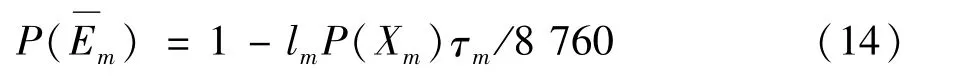
式中lm为线路长度；τm为线路故障修复时间。

若元件En为变压器、断路器、隔离开关等元件，则其正常工作的区间概率为：

2.3.2 配电系统可靠性指标推算

配电系统一般由多个由负荷点{LP1，LP2，…，LPn}构成，其可靠性评估指标由每个负荷点故障区间概率和停运区间概率综合计算得到，包括系统平均停电频率SAIFI（次/用户·年）、系统平均停电持续时间SAIDI（小时/用户·年）、用户平均停电持续时间CAIDI（小时/停电用户·年）和供电可用率ASAI（%）。

式中τn为元件故障修复时间。

则负荷点LP的停运区间概率P（LP）为：

式中P（XLPi）为超椭球模型约束下负荷点LPi的故障区间概率；P（LPi）为负荷点LPi的停运区间概率；Ni为负荷点LPi的用户数。

2.4 配电系统薄弱环节的辨识

若已知叶节点区间概率P（XLP），应用贝叶斯网络概率推理可得根节点Xi的后验区间概率P（Xi|XLP）为：

由式（21）可得当负荷点发生故障时各相关元件发生故障的概率大小，从而可以辨识引起负荷点故障概率大的元件，进而对系统可靠性进行优化。

3 算例分析

为验证本方法的有效性，现以IEEE-RBTS Bus 6母线系统为例进行算例分析。该系统是一个具有子馈线的复杂配电系统，由负荷点、线路、变压器、熔断器、断路器和隔离开关组成，如图2所示。

图2 IEEE-RBTSBus 6母线系统Fig.2 IEEE-RBTS 6 bus system

设该系统各负荷点用户数相同，各线路均为1 km，线路故障修复时间为6.5 h，变压器故障修复时间为200 h，断路器和隔离开关故障修复时间为4 h。由证据理论获取的各元件初始故障区间概率和由超椭球模型约束的区间概率见表1。

表1 元件故障区间概率Tab.1 Interval failure probability of components

根据系统拓扑结构分别对各负荷点贝叶斯网络进行构造，以负荷点LP18为例，如图3所示。根节点X1，X2，X3分别表示线路L35、线路L36和变压器T18出现故障，叶节点XLP18表示该负荷点出现故障。

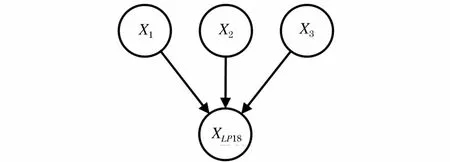
图3 负荷点LP18的贝叶斯网络Fig.3 Bayesian network of load point18

根据贝叶斯网络分别对各负荷点停运区间概率和配电系统可靠性评估指标进行推算。部分负荷点停运区间概率见表2，系统可靠性评估指标见表3。

表2 部分负荷点停运区间概率Tab.2 Outage interval probability of partial load points

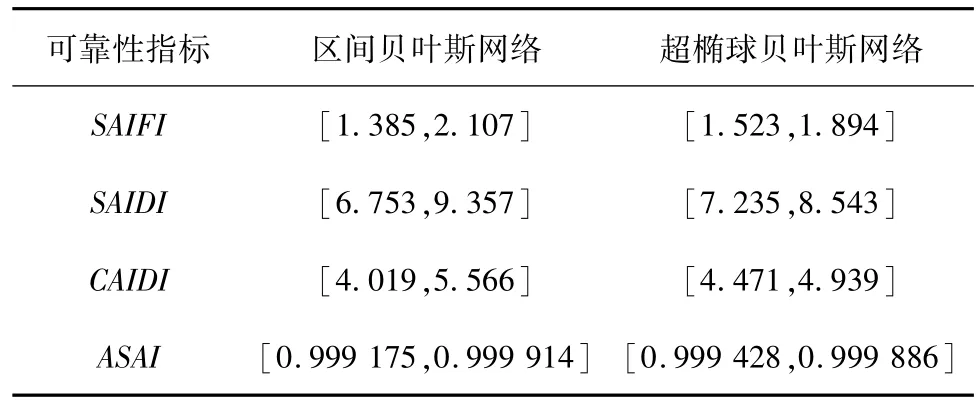
表3 系统可靠性评估指标Tab.3 System reliability assessment indices

由表2与表3可得，本方法的计算结果与文献［15］接近，证明了本方法在配电系统可靠性评估中的可行性。同时，本方法的计算结果相比于区间贝叶斯网络法区间更小，证明了本方法可以较好地弥补区间模型计算结果相对保守的不足，更加符合工程的实际情况。

根据贝叶斯网络对负荷点发生故障时元件的后验区间概率进行推算，以负荷点LP7为例，见表4。

由表4可知，当负荷点LP7发生故障时，元件L15，L17，L19，L21的后验区间概率相对较大，因而这些元件是对配电系统进行失效诊断或预防维修时应重点关注的元件。

表4 元件后验区间概率Tab.4 Posterior interval probability of components

4 结束语

在实际配电系统可靠性评估的过程中，为尽可能考虑各非精确失效概率对评估结果的影响，本文将超椭球模型与贝叶斯网络相结合，提出了一种新的可靠性评估方法。该方法应用超椭球模型约束由证据理论获取的贝叶斯网络根节点区间概率，并通过双向推理获取叶节点区间概率和根节点后验区间概率，进而获取配电系统可靠性评估指标范围并辨识系统的薄弱环节，可为配电系统规划、可靠性优化等问题提供理论支持。算例分析证明了该方法适用于评估实际配电系统的可靠性。