风向空间分散性及其对全场风电功率预测误差的影响*
2017-12-20刘红柳杨茂于宁张强
刘红柳,杨茂,于宁,张强
(1.东北电力大学电气工程学院,吉林吉林132012;2.国网大连供电公司,辽宁大连116021)
0 引 言
电力是关系国民经济和社会发展的重要基础性产业,也是关系国计民生和国家能源安全的公共事业。由于日益加重的资源短缺和环境压力,电力的可持续发展问题已成为世界各国关注的焦点问题[1]。风能是至关重要的低碳能源,有实现可持续能源供应的潜力。随着风电渗透进电网容量的持续增加,风能自身的不确定因素会严重影响电能质量和电力系统运行,比较准确的预测风电功率,可以帮助电力系统调度部门做出合理的发电调度决策,从而减轻风电对电网的影响[2]。
国内外主要通过提高风速预测精度来改善风电功率预测精度[3-4],目前国内风电场风速预测均方根误差在10%~25%左右,这不仅与预测周期以及预测地点的物理因素(如:风速特性,温度,湿度等)有关,还与风速预测方法有关[5-6]。文献[7]提出一种分形自回归综合滑动平均模型(f-ARIMA),对风速进行提前24 h和提前48 h的预测。文献[8]提出了一种基于人工神经网络的改进经验模态分解方法来进行风速的预测,所建立模型的风速预测精度有所改善。文献[9]基于混合预测模型对风速进行预测,利用卡尔曼滤波对人工神经网络的预测结果进行修正,取得较好效果。但风速为矢量,包括速度(大小)和风向(方向)两个因素,上述方法只考虑风速的大小,并未考虑风向的影响。文献[10]指出在对风电场功率进行超短期预测时,将风电场所有机组等值为一台机进行整体预测的不足之处,验证了机组的不同布局方式对整体预测功率的影响,并建立考虑风向的风电场超短期功率预测模型,证明了在进行风速预测的同时进行风向预测可以提高功率预测精度。文献[11]提出一种空间相关模型,将风电场风力机之间出力的不确定性关系转化为相对量化的确定性关系,在传统预测方法的基础上,考虑风力机之间的尾流效应,推导出了风电场动态空间矩阵,通过空间相关模型计算所得出的功率值更符合风力机实际运行中的出力。文献[12]研究了风电机组尾流效应对风电场输出功率的影响。国内外学者对风向影响风电功率预测的研究主要集中在风电场布局和尾流效应等方面,目前还没有考虑风向空间分散性的相关研究。风电场的风不会时刻都垂直作用在风机的风叶上,因此预测所得风速值并不是完全作用在风机上的有效风速,风速与风机间有一定的夹角,通过受力分析可知,有效风速为实测风速在风叶方向投影所得到的垂直分量。因此风向决定了作用在风机轮毂高度的有效风速,利用风向预测有效风速可以改善风电功率预测精度。
文章以我国某风电场为例,提出了考虑风向空间分散性的预测方法,原始数据是10 min间隔的风速时间序列、风向时间序列和风电机组输出功率的时间序列。本文研究的主要内容包括:风电场内各机组风向的空间分散性;考虑风向空间分散性的全场功率计算;分析风向的空间分散性对全场风电功率预测误差的影响;计算预测误差并给出各误差间的相互关系。
1 风电场内各机组风向的空间分散性
通常风电场内包含多台风机,大型风电场风电机组数量可多达几百台,覆盖面积可达几十平方千米以上,再考虑到风电机组之间的相互影响,某时刻不同风机处的风向不可能完全相同。风电场一般每台风机均配有数据实时采集系统,可实时采集单台风机处的风速、风向和输出功率值,这为分析风向的空间分散性及其对全场风电功率计算的影响提供了数据来源。
t时刻风电机组i的风向αi(t)可以表示为全场平均风向)与本机风向空间偏差量 Δαi(t)之和,即:


各风电机组风向的空间偏差量Δαi(t)刻画了风电机组风向的空间分散性。


显然,对于全部风向空间偏差量,有:说明在每一个时刻,风向空间偏差量的均值为0;也说明平均风向是对t时刻所有机组风速总体强度的一个无偏估计。一般风电场覆盖区域较大,风向的空间分散性普遍存在。
图1给出了一个具有177台1.5 MW风电机组的吉林省xx风电场2014年8月11日3时20分的风向空间分布,此刻全部机组的风向分布在201.43°~279.94°之间,平均风向为 255.36°,风向变化的标准差为 11.23°。

图1 xx风电场177台风电机组在2014年8月11日3时20分的风向空间分布Fig.1 Spatial distribution of wind direction for 177 wind urbines in xx wind farm at3:20am,11th,Aug.2014
图2给出了xx风电场2014年8月11日全天各风电机组最大最小风向的时序曲线,说明了各机组风向空间分散性随时间变化的情况。
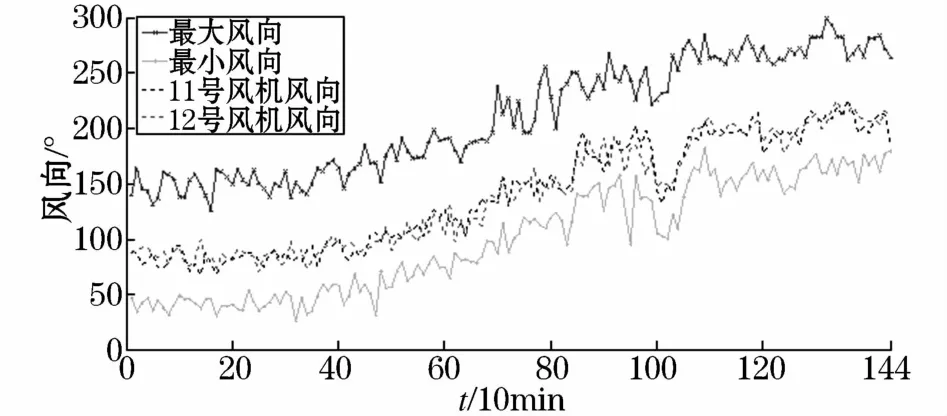
图2 xx风电场全天风向最大值、最小值时序图(2014年8月11日)Fig.2 Sequence diagram of the maximum and minimum wind direction in xx wind farm in one day(11th,Aug.2014)
由于任意时刻 αmax(t)≠αmin(t),风向的空间分散性普遍存在。
可以用t时刻风电场内n台机组风速的标准差S(t)来度量风速空间分散性的强度。

图3给出了xx风电场在2014年8月各机组风向偏差量的标准差,标准差的均值为14.92°。

图3 xx风电场一个月各机组风向空间变化的标准差(2014年8月)Fig.3 A standard transformation curve from wind direction to power of a 1.5 MW wind turbine
由图1~图3可以得出结论:各机组的风向存在显著的空间分散性。
2 考虑风向空间分散性的全场功率计算
2.1 有效风速与风向之间的关系
风电场的风不会时刻都垂直作用在风机的风叶上,因此预测所得风速值并不是完全作用在风机上的有效风速,风速与风机间有一定的夹角,通过受力分析可知,有效风速为实测风速在风叶方向投影所得到的垂直分量。
考虑风向空间分散性也就是计及单台机组的实际风向,如图4所示为考虑风向空间分散性情况的有效风速计算示意图:已知t时刻各风电机组的风速vi(t),单台机组风向 αi(t),测风塔风向 αcefengta(t),以测风塔处风向为x轴建立直角坐标系,风电场每台风机的有效风速即为实测风速在x坐标轴上的投影值,t时刻单台风机风向与测风塔风向夹角为,(αi(t)-αcefengta(t)),则:
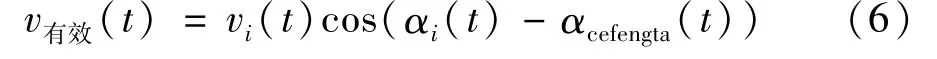

图4 (计及实际风向)实际风速在测风塔风向方向的投影坐标图Fig.4 Projection coordinate graph of actual wind peed in the direction of the wind tower wind direction considering the actual wind direction

图5 (计及平均风向)实际风速在测风塔风向方向的投影坐标图Fig.5 Projection coordinate graph of actual wind speed in the direction of the wind tower wind direction considering the average wind direction
忽略风向空间分散性也就是计及全场机组的平均风向,图5所示:已知t时刻各风电机组的风速vi(t),整场机组平均风向(t),测风塔风向αcefengta(t),以测风塔处风向为x轴建立直角坐标系,风电场每台风机的有效风速即为实测风速在x坐标轴上的投影值,t时刻整场机组平均风向与测风塔风向夹角为,则:
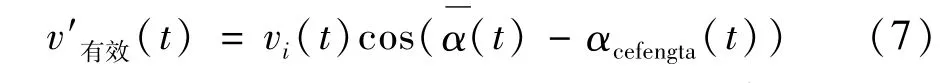
2.2 风电场的风速风向与全场总功率计算的关系
风电场的总功率是由各机组功率累加而成的,本文不计风向对各机组传变特性的影响,只考虑静态的风速-功率变换关系,即用标准风速-功率传变特性表示全场所有风电机组的输入输出关系。为了揭示风向空间分散性与全场风电功率计算误差之间的关系,暂假设不计风速预测误差。严格地讲,这意味着t时刻每台风电机组的风速均得到准确预测,事实上这一条件很难实现。退化这一条件,取实际的平均风速(风向)作为预测的平均风速(风向)(相当于精确的平均风速(风向)预测),取实际的风速(风向)作为预测的单台风机风速(风向)(相当于精确的单台风机风速(风向)预测),则有如下关系:
(1)整场实际功率

(2)不考虑风速空间分散性(以平均风速计算)预测整场功率

式中
(3)考虑风速空间分散性(以实际风速计算)预测整场功率

式中 vi(t)为第i台风机t时刻实际风速值;(t)为t时刻考虑风速空间分散性整场风电功率预测值。
(4)不考虑风向空间分散性(以平均风向计算)预测整场功率

(5)考虑风向空间分散性(以实际风向计算)预测整场功率

式中 vi(t)cos(αi(t)-αcefengta(t))为考虑风向空间分散性情况下第i台风机t时刻的有效风速;Pα∑(t)为t时刻考虑风向空间分散性情况的整场风电功率预测值。
3 算例分析
仍选取吉林省某风电场2014年8月1日至2014年8月30日每台风机的功率、风向和风速数据,风电场额定装机容量为265.5 MW,时间尺度为10min。
取实际的平均风速(风向)作为准确预测的平均风速(风向),取实际的单台风机风速(风向)作为准确预测的单台风机风速(风向)。图6给出了xx风电场2014年8月7日用标准风速-功率传变特性计算得到的风电场总功率。不考虑风向空间分散性(平均风向,点实线)预测整场功率和考虑风向空间分散性(实际风向,虚线)预测整场功率(t)计算结果。两条曲线的最大偏差达到装机容量的2.27%,说明若不计风向的空间分散性,只由平均风向计算全场风电功率会有较明显的误差。
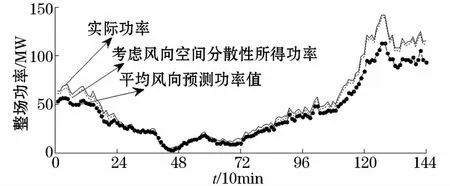
图6 某风电场由平均风向,实际风向算出的总功率和实际总功率(2014年8月7日)Fig.6 Total wind power calculated by average wind direction,actual wind direction and actual total power in a wind farm(7th,Aug.2014)
图7为某风电场(装机容量265.5 MW)2012年8月7日,考虑风向空间分散性(实际风向,点实线)预测整场功率(t)和以平均风速预测整场功率(t)(虚线)的计算结果,实线表示实际功率。点实线与实线两条曲线的最大偏差达到装机容量的1.67%,虚线与实线两条曲线的最大偏差达到装机容量的5.92%说明若不计风向的空间分散性,由平均风速计算全场风电功率会有较明显的误差。
图8为某风电场(装机容量265.5 MW)2012年8月7日,考虑风向空间分散性(实际风向)预测整场功率 Pα∑(t)和考虑风速空间分散性 Pv∑(t)(实际风速)预测整场功率。
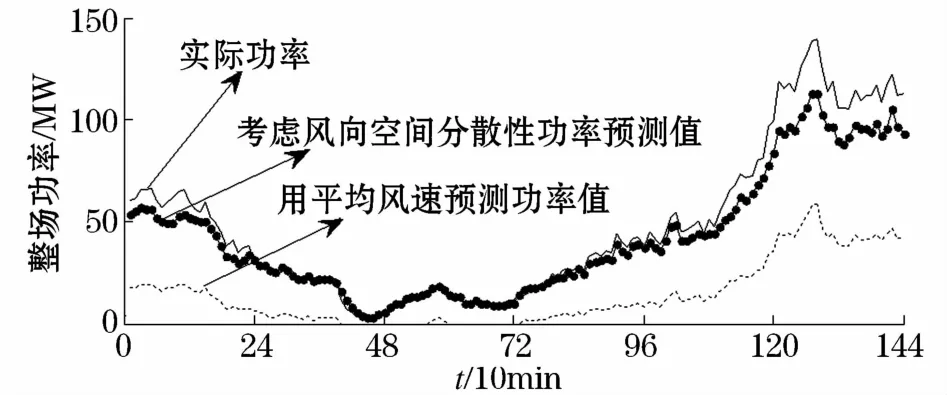
图7 某风电场由平均风速,实际风向算出的总功率和实际总功率(2014年8月7日)Fig.7 Total wind power calculated by average wind speed,actual wind direction and actual total power in a wind farm(7th,Aug.2014)

图8 某风电场由实际风速,实际风向算出的总功率和实际总功率(2014年8月7日)Fig.8 Total wind power calculated by actual wind speed,actual wind direction and actual total power in a wind farm(7th,Aug.2014)
与实际功率曲线对比,发现考虑风速空间分散性曲线更贴近实际功率曲线,即在考虑风速空间分散性基础上考虑风向空间分散性,可以提高预测精度。考虑风向空间分散性的整场风电功率预测效果更好。
4 风向空间分散性与风电功率预测误差分析
4.1 四种风电功率预测方法预测误差对比分析
如果取实际的平均风速、风向作为预测的平均风速、风向的假设下,风电功率的计算误差就相当于最小预测误差。
表1给出了2014年8月该风电场考虑实际风速实际风向的整场风电功率预测误差、考虑实际风速平均风向的整场风电功率预测误差、仅考虑实际风速的整场风电功率预测误差((t))和仅考虑平均风速的整场风电功率预测误差()的分析结果。
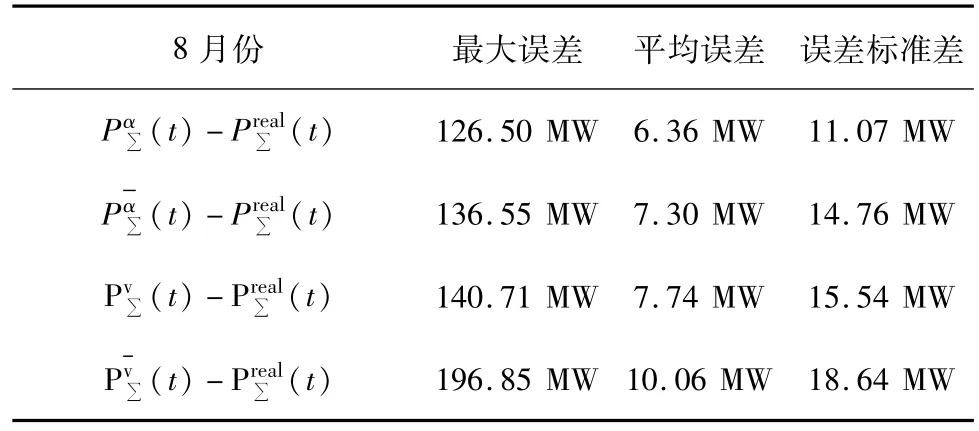
表1 2014年8月4种预测风电功率方法预测误差统计Tab.1 Error statictics of 4 wind power prediction methods in August2014
由表1可见,预测精度由高到低依次是:考虑实际风速和实际风向>考虑实际风速平均风向>仅考虑实际风速>仅考虑平均风速。因此考虑风向空间分散性(考虑实际风速和实际风向)预测整场风电功率的预测效果最好,说明考虑风向空间分散性可以提高是全场风电功率预测精度。在风速空间分散性基础上考虑风向空间分散性(即考虑实际风速风向计算整场功率)可以降低全场风电功率预测误差。
4.2 四种风电功率预测方法预测误差对比分析
忽略风向空间分散性带来的误差:
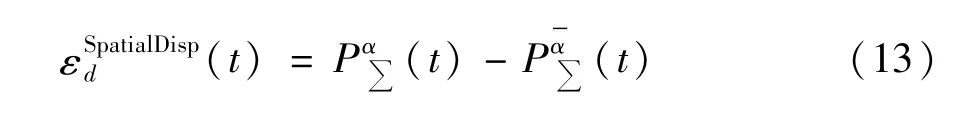
全部计算误差:

一定时段[0,T]内误差变化的分布特性可用标

η的值越大,表明风向空间分散性导致的误差在总误差中所占比例大,亦即对风电功率预测误差的影响大。
表2给出了2014年8月该风电场因不计风向空间分散性带来的风电功率预测误差的分析结果。
由表2可见,即使在风速和风向预测完全准确的情况下,风电功率计算的总误差达到装机容量的1.18%(均值)和1.83%(标准差),而风向空间分散性引起的误差在总误差中分别占40.31%(均值)和31.27%(标准差)。说明风向空间分散性是产生全场风电功率预测误差的重要组成部分。

表2 2014年8月风向空间分散性误差及总误差Tab.2 Error of wind direction spatial dispersion and the total error in August2014
5 结束语
研究了风电场内各机组风向的空间分散性及其对全场风电功率计算和预测准确性的影响。某一时点风电机组实际风向相对于平均风向的空间偏差量刻画了风向的空间分散性。建立了评价风向空间分散性对风电功率预测误差影响的分析架构,给出了误差之间的关系。某风电场的实测数据算例结果表明:
(1)风电场风向空间分散性普遍存在;
(2)考虑风向空间分散性可以减小全场风电功率预测误差,忽略风向空间分散性带来的误差在总误差中的占比达30%以上;
(3)在风速空间分散性基础上考虑风向空间分散性可以降低全场风电功率预测误差。
