基于Copula理论和切片采样技术结合拉丁超立方抽样的概率潮流计算*
2017-12-20毛晓明叶嘉俊魏焕政李牧星
毛晓明,叶嘉俊,魏焕政,李牧星
(广东工业大学自动化学院,广州510006)
0 引 言
电力系统存在大量的随机性因素,随着风、光等可再生能源发电大规模并网,不确定性因素进一步增加[1-3]。Borkowska于 1974年提出的概率潮流(Probabilistic Load Flow,PLF)分析方法通过计算节点电压、线路功率及网损率的期望、方差、概率密度函数(Probability Density Function,PDF)及累积分布函数(Cumulative Distribution Function,CDF)等,掌握系统稳态运行的概率统计特性[4]。
PLF计算方法有多种。其中,MCS方法虽有计算效率低等不足,但仍被认为是最强大、最灵活和最准确的PLF分析方法[5]。针对MCS的不足,人们将马尔科夫过程(Markov Process,MP)引入到MCS中,形成了马尔科夫链蒙特卡洛(Markov Chain Monte Carlo,MCMC)模拟法[6-7]。可是,广泛用于构建马尔科夫链的Metropolis-Hastings算法和Gibbs算法也存在如下不足:(1)Metropolis-Hastings算法需先指定一个便于随机数生成的“建议”分布函数,而给复杂的分布函数指定一个合适的“建议”分布函数是很困难的;(2)Gibbs算法需要先确定参数的满条件分布,但满条件分布复杂的变量无法直接采样。这些缺点限制了MCMC方法的广泛使用。
针对上述问题,文献[8]将切片采样(Slice Sampling,SS)技术[9]引入到电力系统 PLF中,提高了传统MCMC方法的计算精度及效率。本文在文献[8]的基础上,进一步引入Copula理论和拉丁超立方抽样,以计及输入变量间的相关性并提高计算效率,形成 CMCMCS-CI(Correlation Slice Sampling MCMC Simulation with Copula and Improved Latin Hypercube Sampling)算法。新方法采用Kendall秩相关系数度量随机变量的相关程度,采用切片采样的MCMC算法和Copula理论实现相关随机变量初始样本的采样,采用改进的拉丁超立方采样对初始样本进行处理,降低样本规模,在考虑随机变量相关性的同时,进一步提高MCMC方法的计算效率。以改造后的IEEE-14节点测试系统为算例,验证了所提方法的准确性和有效性,在此基础上研究风、光出力相关性对电力系统概率潮流的影响。
1 Copula理论
通常由随机变量的联合分布可以方便地确定各自的边缘分布,但由随机变量的边缘分布却很难确定其联合分布。Copula理论的提出和完善,一定程度上解决了这一问题[10],本文采用该理论来建立潮流计算中随机关联性变量的概率分布模型。
1.1 Copula理论简介
Copula理论认为一个N维联合分布函数可以分解为N个边缘分布函数和一个连接Copula函数,且变量间的相关关系可由这个连接函数表示[11]。Nelsen于2006年给出了 Copula函数的严格定义[12]:Copula函数是将随机向量X1,X2,…,XN的联合分布函数 F(x1,x2,…,xn)与各自边缘分布函数 FX1(x1),FX2(x2),…,FXN(xn)相连接的连接函数,即存在函数C(u1,u2,…,un)使:
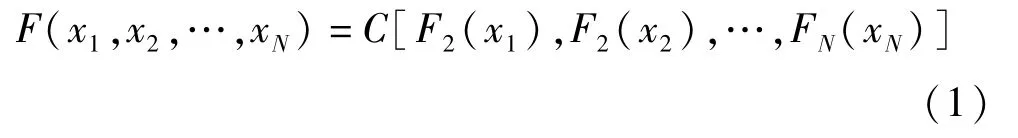
Copula函数种类多样[13],其中阿基米德Copula函数具有优良的性质,已广泛应用于各个领域。
1.2 Copula函数的相关性测度
随机变量间相关性度量的方法有很多,Kendall秩相关系数τ有诸多优点[14],本文选取Kendall秩相关系数。
设(x1,y1),(x2,y2)是二维随机向量(X,Y)的 2个观测值,如果(x1-x2)(y1-y2)>0,则称(x1,y1)和(x2,y2)是和谐的(concordant);若(x1-x2)(y1-y2)<0,则称它们是不和谐的(discordant)。
设(X1,Y1),(X2,Y2)是相互独立且与(X,Y)同分布的二维随机向量,则Kendall秩相关系数τ定义为:

式中 P[(X1-X2)(Y1-Y2)>0]、P[(X1-X2)(Y1-Y2)<0]分别表示和谐及不和谐的概率。τ∈[-1,1]。τ∈[-1,0)、τ=0和 τ∈(0,1]分别表示随机变量负相关、不能确定相关关系及正相关。
Kendall秩相关系数τ可由Copula函数计算得到。例如,若随机变量w1和 w2的 Copula函数为C(F1(w1),F2(w2)),则 τ可由下式得到[13]:

2 采样算法
2.1 切片采样算法
切片采样是一种广义的Gibbs采样算法,在构造可逆马尔科夫转移核时要先预定义一个恒定分布[15]。欲从集合Rn中抽取服从某个概率分布的变量x,且其概率密度函数 g(x)与某一函数 f(x)成正比,我们可以通过对g(x)曲线下方的(n+1)维空间随机均匀采样得到。
引入附加变量y,定义关于x和y的联合分布,其中y在曲线 f(x)下的区域为 U={(x,y):0<y<f(x)},则(x,y)的联合概率密度函数 f(x,y)可以表示为[9]:

式中Z=∫f(x)d x。变量x的边缘密度函数为:
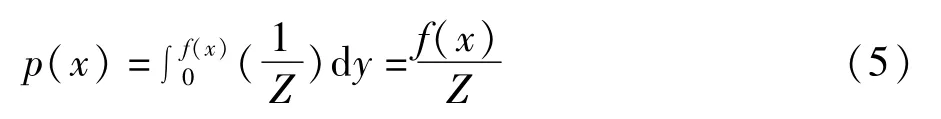
对(x,y)进行抽样,然后消去附加变量y即得到变量x的样本。具体迭代步骤为:
(1)从区间(0,f(x0))随机均匀生成 y,其中 x0为给定的初值,切片S(由y来定义)对应的横轴x值的集合为{x:f(x)>y};
(2)确定以x0为扩张基点且覆盖S绝大部分区间的采样区间 I=(L,R);
(3)从区间I均匀随机地生成新变量x1。
单变量切片采样算法的示意图如图1所示。图中由y确定的水平切片S被曲线f(x)分割成许多小切片 S1、S2、S3,且与 S对应的横轴 x值均满足f(x)>y;以x0为基点的样本区间扩张到S外的区域前,宽度以w为步长持续增加,然后在扩张后的样本区间I=(L,R)均匀随机地生成新变量 x1。

图1 单变量概率密度函数的切片采样算法实现示意图Fig.1 Single-variable slice sampling by simulating a sample from the region under its density function
由于函数f(x)的起伏会把水平切片S切割成许多小切片,使区间I呈现多重边界,且有些概率密度模型很复杂,因此如何确定采样区间成为切片采样最棘手的问题。
针对这种情况,Neal提出了“Stepping-out”和“Shrinkage”算法来确定区间I的边界。首先,以x0为基点定义一宽度为w的微型水平区间I。然后以w为步长重复扩张区间I,直到该区间超出水平切片S的范围,即 f(x)≤y。由于采样区间 I=(L,R)对应的横轴x值不一定全部满足f(x)>y,所以若新生成的随机数x1位于切片S外部,则收缩区间I两端,然后再次生成x1,重复此过程直到生成的x1满足f(x1)>y为止。随着不满足条件的随机变量不断被拒绝及区间I的收缩,符合条件的随机数x1的生成概率逐渐增加。详细步骤见文献[9]。
通过与Gibbs算法类似的采样方式(即:将每个变量的分布函数当作条件性依赖于其它变量当前值的单变量概率模型)对不同变量轮流依次采样即可实现对多元分布概率模型的采样。
将该算法应用于PLF中,可改善采样值在随机变量分布中的覆盖程度、提高样本采样效率,并显著提高传统MCMC方法的计算准确度[8]。
2.2 改进的拉丁超立方采样方法
传统的拉丁超立方采样(Latin hypercube sampling,LHS)[16]在对随机变量 w进行采样时,需要知道随机变量的CDF表达式。但在很多情况下,w的CDF是未知或难以求取的,这就限制了LHS的应用。针对这一不足,文献[17]提出了一种基于离散数据的改进拉丁超立方采样方法(ILHS),该方法只需依赖于随机变量的CDF特性。
对于单个输入随机变量w1,在已知n个离散数据 W1×n=[w1,w2,…,wn]的情况下,W1×n中任意样本发生的概率为1/n。如果将w1的边际累积分布函数均匀地分割成N个互不重叠的区间,那么每个区间包含 n/N个离散数据,则样本 W‴1×N=[w‴1,w‴2,…,w‴N](N≤n)可以通过下列步骤得到:
(1)将离散数据W1×n由小到大进行排序,得到向量 W′1×n=[w′1,w′2,…,w′n];
(2)将向量 W′1×n的第 i个元素 w′i赋值给向量W″1×N的第 k(k=1,2,…,N)个元素 w″k,即 w″k=w′i,其中i与k的关系如式(6)所示:

(3)对样本 W″1×N=[w″1,w″2,…,w″N]进行随机排序,即可得到样本 W‴1×N=[w‴1,w‴2,…,w‴N]。
对于 m维输入随机变量向量 Wm×1=[w1,w2,…,wm]T,在已知n组离散数据 Wm×n=[w1,w2,…,wm]T(wj=[wj1,…,wjn],j=1,2,…,m)的情况下,可由下列步骤得到相应的LHS样本矩阵Wm×N:
(1)采用单变量的ILHS方法对输入随机变量w1的n个离散数据w1=[w11,…,w1n]进行采样,获得样本 w‴1=[w‴11,w‴12,…,w‴1-N];
(2)计算变量 w1的样本 w‴1的第 i(i=1,2,…,N)个元素 w‴1(i)在 w1=[w11,…,w1n]的位置参数li,即 w‴1(i)=w1(li);
(3)对于 Wm×1=[w1,w2,…,wm]T的第 h(h=2,…,m)个变量 wh,ILHS采样得到的样本为 w‴h=[w‴h1,w‴h2,…,w‴hN],其中 w‴h的第 i个元素 w‴h(i)为 wh=[wh1,wh2,…,whN]的第 li个元素 w″h(li),即w‴h(i)=w″h(li);
(4)重复步骤(3)即可得到所有随机变量的LHS采样样本,从而得到随机变量向量Wm×1的样本矩阵W‴m×N=[w‴1,w‴2,…,w‴m]T(w‴i=[w‴i1,w‴i2,…,w‴iN],i=1,2,…,m)。
步骤(3)确保了样本矩阵 W‴m×N中随机变量的相关性与Wm×n中随机变量相关性的一致。
将ILHS应用于SS生成的初始样本中,在保证随机变量相关性的同时,进一步减小PLF的计算样本的规模,进一步提高MCMC方法的计算效率。
3 基于CMCMCS-CI采样的概率潮流计算方法
生成满足相关性及边缘分布等要求的输入随机变量的样本,是基于CMCMCS-CI采样的概率潮流计算方法的关键。根据生成的样本通过潮流方程式(7)计算得到系统节点电压D及支路潮流H的值。

式中W节点注入功率向量;D为节点电压状态向量;H为支路输出功率向量;f和g分别为节点功率和支路潮流方程。
具体步骤如下:
(1)输入基础数据,包括配电网结构参数、节点注入功率 Wm×1=[w1,w2,…,wm]T及采样规模N等;
(2)根据节点注入功率Wm×1间的相关关系选择合适的Copula函数描述其相关结构;
(3)根据选择的Copula函数采用切片采样算法采样得到注入功率 Wm×1初始样本矩阵 Wm×n=[w1,w2,…,wm]T(wj=[wj1,…,wjn],j=1,2,…,m);
(4)采用ILHS方法对初始样本矩阵 Wm×n进行采样获得最终样本矩阵 W‴m×N=[w‴1,w‴2,…,w‴m]T(w‴i=[w‴i1,w‴i2,…,w‴iN],i=1,2,…,m);
(5)将N组节点注入功率Wm×1的采样值分别带入式(7)依次采用牛顿-拉夫逊算法进行N次确定性潮流计算,获得N组节点电压、支路潮流等输出随机变量的计算值;
(6)应用统计学的方法统计节点电压、支路潮流等输出随机变量的数字特征和概率分布。
4 考虑相关性的风-光联合出力模型
本文建立风电场及光伏电站联合出力模型,研究高比例风、光并网对电力系统概率潮流的影响。
4.1 风力发电出力概率模型
研究表明,世界上大部分地区风速和风电场有功输出满足线性关系[18],即风电场出力Pw的累积分布函数F(pw)和概率密度函数f(pw)可表示为:
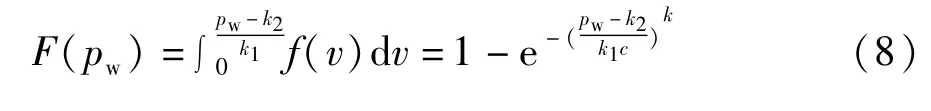

式中风电场风速 v服从Weibull分布,且k、c分别代表Weibull分布的形状参数和尺度参数;k1=Pr/(vr-vci);k2=-k1vci;Pr、vci、vr分别表示风电场的额定输出功率、切入风速和额定风速。
4.2 光伏发电出力概率模型
据统计,世界上绝大部分地区的光伏输出功率ppv的概率密度函数 f(ppv)和累积分布函 F(ppv)数可表示为[2]:
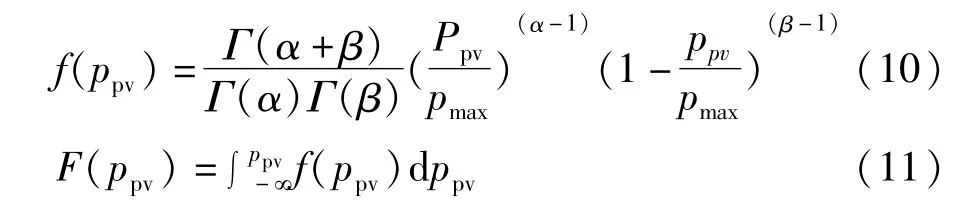
式中Γ表示Gamma函数;α、β分别表示Beta分布的形状参数;ppv、pmax分别表示光伏电站的实际和最大有功出力。
4.3 考虑相关性的风-光电场联合出力模型
本文关注的是风、光电场出力特性对电力系统概率潮流的影响,故风电场和光伏电站均采用等值集中模型,即风电场等效额定出力为所有风机出力总和;光伏电站额定出力为所有光伏电池出力总和。
考虑到相邻地区的风电和光伏出力存在一定的负相关特性,本文选取Frank Copula函数作为风-光联合出力概率分布的连接函数。Frank Copula函数的密度函数可表示为[13]:

式中θ为随机变量u、v的相关参数且θ≠0;当θ>0时表示 u、v正相关;θ→0时表示 u、v趋于独立;θ<0时表示u、v负相关。
Kendall秩相关系数τ与Frank Copula函数相关参数θ的关系为:

由式(1)、式(12)可得风电场和光伏电站有功出力的联合概率密度函数为:

式中 F(pw)、f(pw)和 F(ppv)、f(ppv)分别为风电场和光伏电站有功出力的分布函数和概率密度函数;相关参数θ可由式(13)求得。
在不同Kendall秩相关系数下,采用本文方法抽样得到的100组风电场和光伏电站出力的样本数据如图2所示。

图2 不同秩相关系数下风、光电场有功出力Fig.2 Active power outputs of wind and photovoltaic farmswith different rank correlation coefficients
5 算例
5.1 测试系统
本文以图3所示改造后的IEEE-14节点测试系统为算例进行仿真分析。假设风电场W接入到节点13,光伏电站PV接入到节点14。系统发电机总装机容量为572.4 MW,新能源装机容量为200 MW,占比34.9%。风机装机容量100 MW,风速服从尺度参数为14.117 8、形状参数为2.017 8的 Weibull分布,且风机的切入、额定、切出风速分别为3 m/s、16 m/s和25 m/s。光伏发电装机容量为100 MW,有功出力服从形状参数为2.06和2.50的Beta分布。假设风电场及光伏电站均采用功率因数为1的恒功率因数控制方式,所有负荷服从期望为稳态值、标准差为期望值15%的正态分布。
5.2 算法验证
采用本文概率潮流计算方法对图3所示系统进行概率潮流分析,并与基于切片采样的MCMC法得到的结果进行比较,验证本文所提方法的准确性和有效性。其中CMCMCS-CI的采样规模为1 000次;切片采样规模分别为105次和103次,认为采样规模为105次时计算所得结果为准确值。

图3 IEEE-14节点算例接线Fig.3 Diagram for IEEE 14-bus system
两种方法所得节点14电压幅值的期望μv、标准差σv,线路6-11有功功率期望μa、标准差σa,系统网损率期望μI、标准差σI如表1所示。
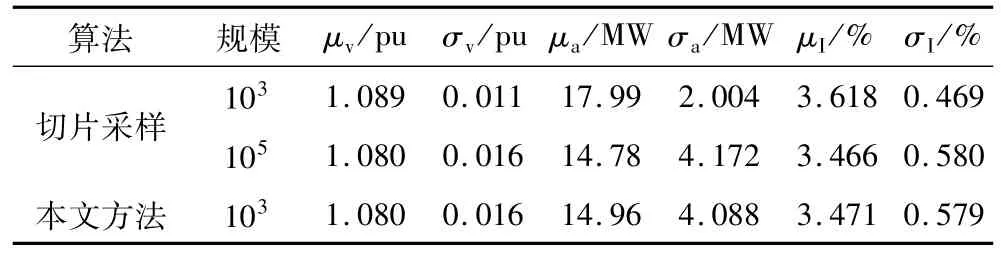
表1 IEEE-14节点系统概率潮流计算结果Tab.1 Probabilistic power flow results for IEEE 14-bus system
可见,采样规模为103时,本文方法即可获得较为准确的结果,耗时304.67 s。而为得到准确的结果,切片法需用时1 861.1 s。充分体现了改进的有效性和高效性。
5.3 风电和光伏出力相关性对系统运行的影响
由于光伏电站晚上不出力而夜晚的风速往往较大,因此地理上毗邻的风电场及光伏电站往往具有较强的负相关关系,但由于风资源和光照等自然因素的随机性,仍存在小部分时间呈现正相关性。而风、光出力相关性会改变含风-光发电系统出力的概率分布,进而影响电力系统潮流分布。目前,关于风电光出力相关性对电力系统概率潮流影响的研究鲜有报道。本文将风、光出力的Kendall秩相关系数τ分别设为 -0.9、-0.6、-0.3、τ→0、0.3、0.6和0.9,采用所提CMCMCS-CI概率潮流计算方法依次计算概率潮流,得到如下结果。
5.3.1 对节点电压的影响
不同Kendall秩相关系数下,系统各节点电压幅值和相角的期望值、标准差的变化曲线如图4所示。风、光的相关性对系统节点电压幅值和相角的期望值影响较小,但对标准差影响较大,风、光接入点最甚且标准差随着τ的增大而增大。
不同Kendall秩相关系数下,节点14电压幅值和相角的概率密度曲线和累积分布曲线分别如图5所示。风、光的相关性会影响系统节点电压幅值和相角的概率分布,τ越大,风、光出力变化的同步性越强,电压幅值和相角的波动范围越大,电压越限的概率也越大。

图4 节点电压幅值、相角的期望和标准差ig.4 Mean values and standard deviations of bus voltagemagnitudes and phase angle
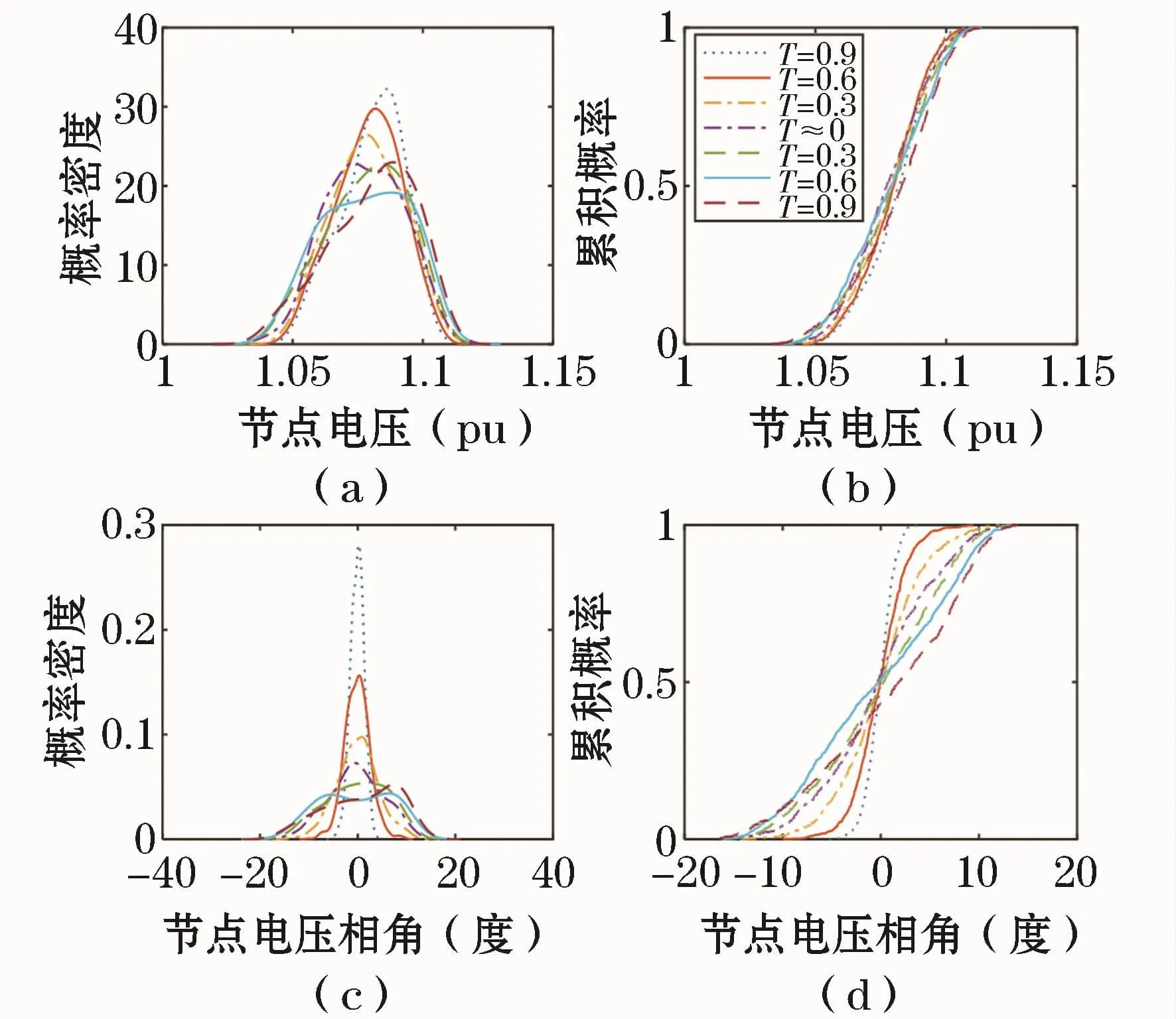
图5 节点14电压幅值、相角的概率密度和累积分布曲线Fig.5 PDF and CDF of voltagemagnitude and phase angle at bus 14
5.3.2 对线路有功的影响
不同Kendall秩相关系数下,系统各线路传输有功的期望、标准差的变化曲线如图6所示。线路有功的期望基本不受风电和光伏出力相关性的影响,但其标准差受到较大的影响,风、光电站之间的线路(线路13-14)有功功率标准差随着τ的增加而减小,其它线路有功功率的标准差随着τ的增大而增大。
不同Kendall秩相关系数下,线路6-11传输有功的概率密度曲线和累积分布曲线如图7所示。风、光的相关性同样会影响线路传输有功的概率分布。随着τ增大,风、光出力变化的同步性增强,线路传输功率波动加剧,越限的概率也增加。
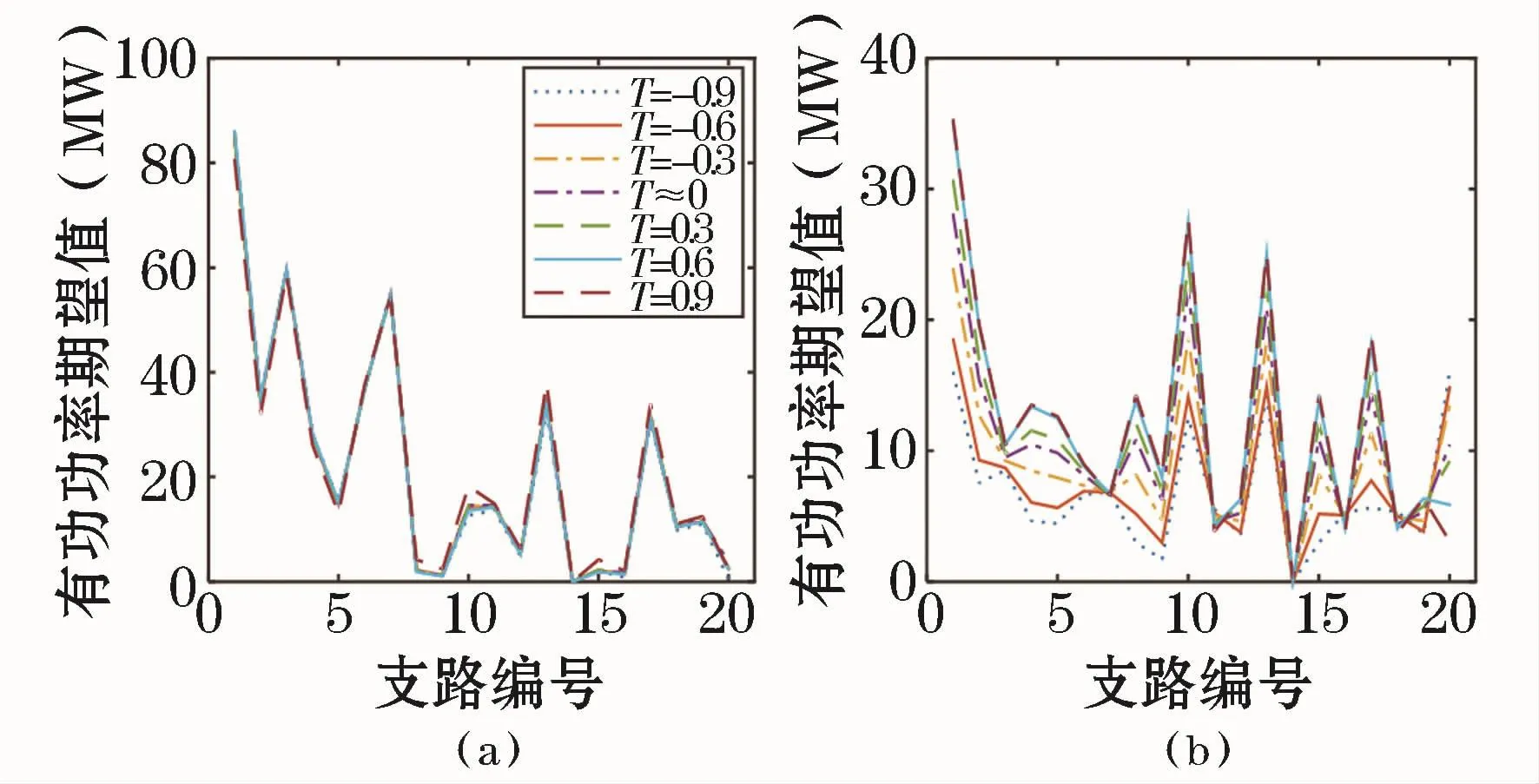
图6 线路有功功率的期望和标准差Fig.6 Mean values and standard deviations of the active power in lines

图7 线路6-11有功功率的概率密度曲线和累积分布曲线Fig.7 PDF and CDF of the active power in line 6-11
5.3.3 对网损率的影响
不同Kendall秩相关系数下,系统网损率的期望与标准差如表2所示。可见,τ增大时,系统网损率的期望μ和标准差σ都会增大。对期望的影响并不显著,最大变化率为12.16%;对标准差影响较大,最大变化率达63.43%。

表2 网损率的期望值与标准差Tab.2 Mean and standard deviations of network loss rate
不同Kendall秩相关系数下,网损率的概率密度曲线和累积分布曲线如图8所示,风、光相关程度会影响系统网损率的概率分布。秩相关系数τ越大,系统网损率变小的概率越大,即风、光互补有助于减小系统功率的损耗。因此,在电力系统分析中,如果低估或忽略风电场和光伏电站出力的相关关系,将无法准确得到系统网损率的概率分布。

图8 系统网损率的概率密度曲线和累积分布曲线Fig.8 PDF and CDF of system network loss rate
6 结束语
本文提出一种基于Copula理论、切片采样技术结合拉丁超立方抽样的MCMC方法,应用于高比例风、光发电并网电力系统的概率潮流计算中。新方法能灵活处理输入随机变量的相关性,在保证精度的同时进一步提高了MCMC方法的计算效率。以改造后的IEEE-14节点系统为算例,验证了方法的准确性和有效性,并得到一些有实际意义的结论:
(1)风电光伏间的相关关系会对概率潮流计算的输出随机变量(节点电压、线路传输功率、网损率等)的期望值、标准差及概率分布产生一定影响,且对期望值的影响较小,对标准差及概率分布影响较大;
(2)随着Kendall秩相关系数τ的增大,输出随机变量(节点电压、线路传输功率、网损率等)的波动性随之增强;
(3)考虑风、光出力的相关性可以更准确地评估风、光并网对电力系统运行的影响,有助于风电场和光伏电站的选址及电网规划。
