非均质性对反求水文地质参数精确性影响研究

(桂林理工大学环境科学与工程学院，广西 桂林 541006)

非均质性对反求水文地质参数精确性影响研究

江凯明

(桂林理工大学环境科学与工程学院，广西 桂林 541006)

地下水文地质参数是衡量含水层导水性质和贮水性质的重要指标，是地下水资源评价的重要基础资料。本文利用GMS软件中的高斯模拟随机场生成不同非均质强度的含水层，对抽水试验进行数值模拟。利用得到的抽水实验数据，分别用解析法和数值法进行反求水文地质参数的计算。分析对比两种方法反求参数的精度，确定两种方法的适用性。结果显示：在反求参数的情况下，解析法要优于数值法；对于推算地下水的水头值时数值法要优于解析法。

非均质含水层；反演；水文地质参数；数值法；解析法

随着科技飞速发展，人类生活的不断提高，人们日益意识到作为国家需求和灌溉的主要来源的地下水，对人类起着主要的生命支撑。水文地质参数(如渗透系数、贮水系数等)是表征含水介质水文地质特性的物理量，衡量含水层导水性质和贮水性质的重要指标，是地下水资源评价的重要基础资料。

确定含水层的水文地质参数是水文地质勘探试验和地下水资源评价中重要的研究工作之一。通常在均质的地下水含水层条件下，不管是用数值法还是解析法，通过抽(注)水试验数据，可以较为精确的求出地下水文参数。而对于非均质地下水含水层，通过抽(注)水试验数据所求的水文地质参数与实际情况会存在一定的误差。理论上认为，数值法的水文地质参数反演要优于解析法。但是解析法的优点是计算简单，所需资料少。本文的研究目的是对不同非均质性的含水层进行数值法和解析法的参数反演，比较反演结果，确定两种方法的适用范围。

1 研究路线与研究方法

本研究选择了渗透系数的地质统计参数(基台值、变程等)作为非均质性的度量，反求参数的精确性则采用反求的渗透系数(采用数值法和解析法分别反求参数)与真实值的差异来衡量。由于比较不同非均质性强度下的反求得到参数的精确性，需要大量的抽水试验数据，而且要在同等条件下比较(即排除其他干扰因素)。因此采用实际的抽水试验不能满足要求。所以本研究采用数值抽水试验来获取大量的数据。

(1)确定研究区边界条件和抽水井位置，观测井和抽水流量；

(2)对研究区渗透系数场赋予不同的地质统计参数(基台值、变程等)，随机生成1组渗透系数场(即1组实现，每组实现的个数为10个)；

(3)根据生成的实现，对研究区进行地下水数值模拟，得到地下水流场，同时也得到了观测井的降深-时间数据；

(4)根据降深-时间数据，分别用数值法和解析法反求渗透系数，将所得的渗透系数与真实渗透系数进行比较；

(5)改变非均质性强度(即地质统计参数)，回到步骤(2)-(4)。

1.1 解析法反求参数原理

本文选取常用的配线法，根据抽水试验数据计算水文地质参数[1-2]。配线法采用Theis公式，该公式假设以下条件成立：

(1)含水层均质各向同性，等厚，侧向无限延伸，产状水平；

(2)完整井定流量抽水，井径无限小；

(3)抽水前天然状态下水力坡度为零；

(4)水头下降引起的地下水从贮存量中的释放是瞬间完成的；

(5)含水层中水流服从Darcy定律。

(1)

其中

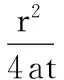
(2)

式中：s为抽水影响范围内，任一点任意时刻的水位降深；Q为抽水井的流量；T为导水系数；t为自抽水开始到计算时刻的时间；r为计算点到抽水井的距离；S为含水层的贮水系数。

本次讨论主要使用Theis模型，对数据进行处理，将进行配线拟合，计算求出的参数。

1.2 数值法反求参数原理

反演方法分为直接法和间接法。利用蒂姆公式或袭布衣公式计算渗透系数，由于反演问题具有多解性和不稳定性这种直接解法计算上稳定性较差，实际计算应用较少。而间接法则是先将一组水文地质参数设为初值，用数值法计算水头，求出计算值与实际观测值的误差，并反复计算水头，直到二者很好拟合为止[3]。下面就对数值法做简要介绍。

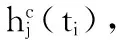
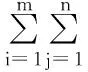
(3)

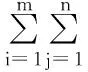
(4)

由(1)和(2)式不难看出，目标函数愈小，拟合效果愈好。只要改变水文地质参数的值，就可以得出不同的目标函数值。解逆问题的实质就是寻找一组水文地质参数，使目标函数与实测值的误差为极小值。

需要说明的是，自然界中的水文地质条件过于复杂，在建立模型时会在一定程度上简化或忽略一些与当前问题无关的条件以方便将实际水文情况概化。这种数学模型是对实际水文地质条件的近似表述，所求得的参数为模型参数，有别于实际的水文地质参数。

1.3 非均质含水层生成

利用GMS软件中的高斯模拟方法来生成非均质性强弱程度不同的渗透参数场[4]。高斯随机域是最经典的随机函数，高斯模型理论通过变异函数可以有助于解决区域化变量的变化及结构性状。变异函数是区域化变量空间变异性的一种度量,它反映了空间变异程度随距离而变化的特征，又能描述其随机性变化。

在生成不同渗透系数的随机空间分布时，需输入渗透系数的地质统计参数，包括变程R、块金常数C0、基台值C，C越大，含水层介质空间关联性越小。

变程的特性表达了区域化变量在变程范围以内，数据所具有的相关性，在变程范围以外，数据之间不相关的特点。通过变程可以反映变量的平面非均质性。

基台值与块金值的比值C0/C，可表示为空间相关度，表示可度量空间自相关的变异所占的比例，表明系统变量的空间相关性的程度。若比值小于25%，说明系统具有强烈的空间相关性，也就是说非均质性程度微弱，或偏向于均质性；若比值在25%～75%之间，表明系统具有中等的空间相关性，可表示为非均质性程度中等；若比值大于75%说明系统空间相关性很弱，可表示非均质性程度较为强烈。块金值与基台值的比值表示随机部分引起的空间异质性占系统总变异的比例。如果该比值高，说明样本间的变异更多的是由随机因素引起的。

本次设计通过全面试验法，控制R值与C值两个变量，对于这两个值分别给予5、10、20、30、40、50、60、70、80、90、100的十一个水平变量，由此可得变量组合有R5C5、R5C10、……、R100C100共121种变量组合，每种组合的算法将随机运算十次，以便对每种组合反演结果进行均值分析，共计生成1 210个K均值为30的不同非均质强度的渗透场。

1.4 研究区介绍及抽水试验的模拟

采用高斯随机场生成含水层, 计算区域面积1 000 m×1 000 m，含水层厚度M=30 m,其储水率SS =0 .005/m ，承压含水层。

图1模拟场等水位图图2 Range(变程)为10时K的误差走势图

含水层的补给为西侧的定水头边界(水头高度为40 m)；含水层的排泄为东侧的定水头边界(水头高度为35 m)和抽水井(图1中红点处，坐标475.3 m，489.2 m;抽水量为4 000 m3/d)；北侧与南侧为不透水边界。

利用上一步生成的渗透场进行模拟抽水试验(抽水试验的时间长度7天)，观测井为图1中灰色点位，共计9个观测井。得到在不同非均质性含水层抽水试验的观测数据。

反演求水文地质参数。

根据抽水试验的数据分别进行数值法和解析法的反求水文地质参数的的计算：

(1) 数值法

利用MOLDFLOW中的Parameter Estimation(参数估计)功能，对稳定抽水试验的数据进行反演计算，对计算所得的渗透系数进行记录；

(2)解析法

利用Theis公式理论对非稳定抽水试验的数据进行反求水文地质参数的计算，对计算所得的渗透系数进行记录。

2 结果及分析

不同变程尺度下，K的绝对值误差随基台值变化走势见图2～图6。

图3 Range(变程)为30时K的误差走势图图4 Range(变程)为50时K的误差走势图

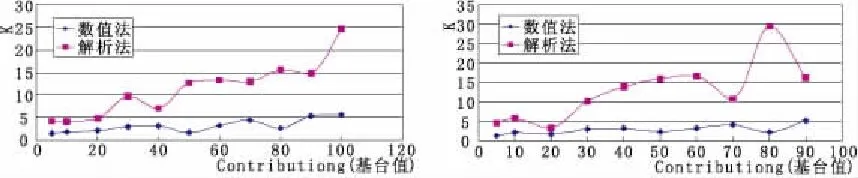
图5 Range(变程)为70时K的误差走势图图6 Range(变程)为90时K的误差走势图

由K的误差走势图可以明显的看出，当Contribuiong(基台值)变大时，也就是非均质强度增大时，无论是解析法还是数值法反求的水文地质参数渗透系数K的误差值都会波动上升；对比解析法和数值法反求参数的误差，当非均质强度增大时，解析法求参数的误差相对较小且更稳定，其绝对值误差都没超过10，而数值法的误差变动较大，起伏不定。

数值法不仅出现了模拟所得计算值徒增突降的现象，而且个别模拟所得的结果大幅波动，误差变动较大，连带着影响该试验整体的精度判断。整体上来说，随着C值的增大，随机参数模拟所得数据的随机性增大，含水层的非均质性不断增强，反演求出的等效渗透系数值与给定的渗透系数值之间的误差也随之增大。对于个别反演所得计算值异常至设定范围极值的现象，并不能说明试验没有价值。针对这一问题，现仅做以下粗略分析：(1)随机参数模拟本身就具有随机性，C值较小时其渗透系数的值是围绕设定的平均值上下产生细微的波动，而C值的增大其波动幅度也随之增大，直接影响则是加大了最值出现的可能；(2)渗透系数可以用正态分布来描述其空间变异性，需考虑随机模拟引起的不确定性

和随机模型中参数的不确定性的影响。

通过对比多组不同Range(变程)下观测井水头误差绝对值变化，以Range为10和30的时候进行举例，如图7～图8。

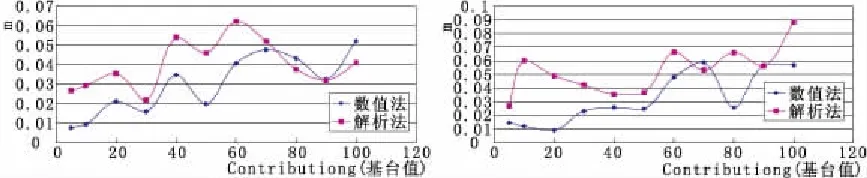
图7 Range(变程)为10时观测井水头误差值走势图 图8 Range(变程)为30时K的观测井水头误差值走势图

结合多组结果可以发现，当非均质程度增大的时候观测井的实际水头与反演水头的误差会波动上升，此时数值法的误差相对较小，并且解析法的计算中随着时间的继续推移水头误差也慢慢的增大。分析其原因推测数值法在利用抽水试验数据时能更好的拟合各个观察孔的数据，因此在推算水头值时具有更高的精度。

3 结语

(1)当非均质的强度增大时，反求渗透系数均值的误差会变大。其中用解析法反求参数会比用数值法反求参数的误差要小。在反求参数的情况下，解析法要优于数值法。

(2)当非均质的强度增大时，数值法反求的各观察孔水头值误差要小于解析法的各观察孔水头值误差。对于推算地下水的水头值时数值法要优于解析法。

(3)通过所得的误差值对比，当基台值不变时，Range的变化对误差值的影响极小。因此不进行对比数据展示。

[1]薛禹群，吴吉春. 地下水动力学[M].第3版，北京.地质出版社.2010.3.

[2]周志芳, 汤瑞凉.基于抽水试验资料确定含水层水文地质参数[J].河海大学学报:自然科学版.1999.27(3):5-8.

[3]刘兴伟，程汤培，邵景力. 地下水流模拟参数估值的并行计算[J]. 计算机工程与设计.2016.(1):189-194.

[4]岳松梅,杨蕴,吴剑锋,等.基于不同地质统计方法的渗透系数场对污染物运移的影响[J].地下水.2014.(4):10-14.

StudyontheInfluenceofHeterogeneityontheAccuracyofReverseHydrologicalGeologicalParameters

JIANGKai-ming

(School of environmental science and engineering, Guilin University of Technology, Guilin 541006, China)

Groundwater hydrogeological parameter is an important index to measure the water conductivity and water storage properties of aquifers, and It is an important basic data for groundwater resources evaluation. In this paper, numerical simulation of pumping test is carried out by using Gauss simulated random field of GMS software to generate aquifer with different heterogeneous strength. Using the pumping experimental data, the analytic method and numerical method are used to calculate the hydrogeological parameters respectively. The accuracy of the two methods is analyzed and compared, and the applicability of the two methods is determined. The results show that the analytic method is better than the numerical method in the case of inverse parameters, and the numerical method is better than the analytic method when calculating the head value of groundwater.

heterogeneous aquifer；inversion；hydrogeological parameters；numerical method；analytic method

P641.73

A

1004-1184(2017)05-0018-03

2017-04-06

国家自然科学基金(41302197)；广西自然科学基金(2013GXNSFBAO19211)

江凯明(1992- )，男，广西柳州人，在读硕士研究生，主攻方向：环境科学。