岩溶管道中悬浮物运移及等参替代数值模型研究——以广西某排泥库悬浮物运移预测为例

，，，，，

(1.南京大学地球科学与工程学院水科学系/教育部表生地球化学重点实验室，江苏 南京 210023；2.南京师范大学虚拟地理环境教育部重点实验室，江苏 南京 210046)

岩溶管道中悬浮物运移及等参替代数值模型研究
——以广西某排泥库悬浮物运移预测为例

周宇超1，祝晓彬1，吴吉春1，吴剑锋1，曾献奎1，郭飞2

(1.南京大学地球科学与工程学院水科学系/教育部表生地球化学重点实验室，江苏 南京 210023；2.南京师范大学虚拟地理环境教育部重点实验室，江苏 南京 210046)

暗河发育岩溶地区地下暗河中污染物的运移模拟研究一直是难点。实际工程应用中，由于传统数值模拟模型没有参数反应悬浮物的沉降作用，通常仅概化考虑悬浮物在地下暗河中的迁移而采用河流一维稳态水质模型进行预测，缺少其它方法进行有效验证。本文通过实验和数值模拟相结合的方法，研究了管径、悬浮物初始浓度、粒径、流速对管道中悬浮物沉降系数的影响，并初步探究数值模型机理相近的吸附系数等效替代一维稳态水质模型沉降系数的可行性，再进一步根据广西某岩溶区排泥库工程构建具体条件下吸附系数与沉降系数的等参替代关系，最后将其应用于数值模型模拟。计算结果表明经过参数等效替代后的数值模拟方法比一维稳态水质模型更为合理。

岩溶；一维稳态水质模型；数值模拟模型；吸附系数；沉降系数

我国岩溶区面积占国土面积近1/3，近年来，随着岩溶区经济的持续发展和矿山的大量开采利用，过程中产生的洗矿泥浆等导致的地下水环境问题受到越来越广泛的关注。有效保护岩溶区地下水环境的前提是对地下水流和溶质运移规律的掌握。

而岩溶区，特别是暗河发育地区，含水介质呈高度管道化和强烈非均质性，使得该区域地下水中污染物运移模拟的研究一直十分困难。实际工程中常用的一维河流稳态水质模型仅将暗河管道作为研究对像，主要考虑污染物的初始浓度、流速和污染物的沉降系数等，而不考虑暗河管道之外区域对污染物运移的影响，其所得结果为一粗略近似解。对于不同分布式模型[1-4]，模型考虑的因素越多，要求获取的岩溶含水系统特征和水文地质参数越精细、越多。而实际岩溶含水系统的暗河发育位置、岩溶管道结构、水流特征、管道-裂隙交互参数等的获取均很难，涉及参数越多，模型实际应用越困难。因此，实际工程应用中，理论模型与实际条件之间达到一定平衡是关键。分布式模型中，等效多孔介质模型[5]因其研究最为成熟、包含此模型的计算软件也最多，涉及参数相对较少，操作简便且可以较好处理岩溶含水介质的非均匀性，被广泛用于模拟岩溶暗河管道的溶质运移问题。

等效多孔介质模型模拟预测岩溶地下暗河悬浮物运移时，目前常用数值模拟软件Feflow由于缺少反映悬浮物运移过程中的沉降特征参数而使其应用受到限制。本文通过实验研究特定条件下数值模型吸附系数与河流解析模型沉降系数的等参替代关系，并以地下暗河发育的广西某岩溶区排泥库工程主要污染物——悬浮物SS在事故工况下的运移预测为例，将等参代替数值模拟模型用于模拟岩溶地下暗河中悬浮物的运移，为数值方法在岩溶区地下水环境影响预测评价中的应用提供成功实践。

1 岩溶暗河悬浮物运移预测评价方法

1.1 河流一维稳态水质模型

河流水质模型是岩溶管道发育地区溶质运移模拟最常用方法[6]。由于泥浆中污染物仅为泥质悬浮物SS，作为保守性污染物，不考虑迁移过程中污染物的源汇项和污染物在地下暗河的吸附、挥发、生物化学反应等，适用于河流一维稳态水质模型[7]：

C=C0×exp[-Kx/(86400u)]

(1)

式中：C0为初始浓度，mg/L；K为沉降系数，1/d；u为地下河流速，m/s；x为沿地下河方向距离，m；c为位于污染源(排放口)下游x处的水质浓度，mg/L；

其中，初始浓度采用充分混合模式求取：

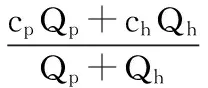
(2)

式中：C0为初始浓度，mg/L；Qp为污水排放量，m3/s；Cp为污染物排放浓度， mg/L；Qh为上游来水量，m3/s；Ch为上游来水污染物浓度，mg/L。

1.2 数值方法

根据研究区水文地质条件，通过分析地下水补、径、排特征，将研究区的地下水流概化成非均质、各向异性、三维非稳定潜水地下水流系统[7]，对应的数学模型如下：

1.2.1 地下水流数学模型

(3)

式中：H0为水头初值；φ1为第一类边界Γ1上的已知函数；q为第二类边界Γ2上的单位面积侧向补给量。n为边界Γ2的外法线方向；Ki,j为各方向上的渗透系数，ω为源汇项，包括降水入渗补给、蒸发、井的抽水量和泉的排泄量等。

基于研究区复杂边界及地下暗河管道的刻画，本文选用有限元法。利用FEFLOW求解水流模型，考虑到模型特点，选择Galerkin有限元法求解，对于潜水面的处理，选择迭代法求解。

1.2.2 溶质运移数学模型

悬浮物在地下水中的运移为三维水流作用下的对流弥散问题，溶液密度假定不变，考虑局部平衡吸附和一级不可逆动力反应。溶质运移的三维水动力弥散方程的数学模型如下[8]：

(4)

式中：

C为为地下水中组分的溶解相浓度，ML-3；θ为为地层介质的孔隙度，无量纲；t为为时间，T；xi为沿直角坐标系轴向的距离，L；Dij为水动力弥散系数张量，L2T-1；Vi为孔隙水平均实际流速，LT-1；qs为单位体积含水层流量，代表源汇项，L3T-1；Cs为源汇项中组分的浓度，ML-3；∑Rn为化学反应项，ML-3T-1。

1)初始条件

将补给浓度边界和注水井处的初始浓度定为C0，其余地方均为0 mg/L，具体表述为：

2)边界条件

本次模拟将含水层各个边界均看做二类边界条件(Neumann边界)，且穿越边界的弥散通量为0，具体可表述为：

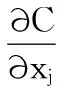
式∞=中：Г2为Neumann边界

溶质运移模型采用FEFLOW求解。

2 岩溶管道悬浮物运移等参替代研究

研究基于不同条件管道悬浮物运移室内实验以及地下水等效介质数值模拟模型和河流一维稳态水质模型。首先设置不同实验条件，通过室内实验获取对应悬浮物浓度。然后以实验设定条件为数值模拟模型和一维稳态模型的构建基础，通过拟合实验实测数据，分别求得数值模型中的吸附系数和一维稳态模型中的沉降系数。最后，通过统计方法，探求沉降系数和吸附系数二者之间的等效关系。

2.1 管道悬浮物运移等参替代影响因素研究

2.1.1 管道悬浮物运移室内实验

实验装置主要有带有恒定水头装置的水箱、胶皮管道、阀门、水泵、针筒、稳流箱、秒表、刻度尺等。实验装置图如图1所示。水箱带有定水头装置，和阀门共同控制泥浆流出速度。管道长20 m，每隔2 m设置观测点，观测点处插入针筒方便采样。

室内实验流程大致如下：预先配好一定浓度的泥浆悬浮液倒入水箱中，打开阀门让泥浆流出，让其在管道中运移，同时不停地往水箱里加泥浆悬浮液使水箱内水头保持不变，运移一定时间后，关掉出水口阀门和尾部阀门，迅速取样。根据泥的质量和泥浆悬浮液体积求得泥浆悬浮液浓度。实验参数表如表1所示。

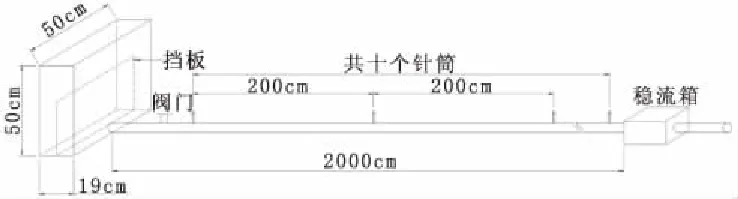
图1 室内实验装置示意图

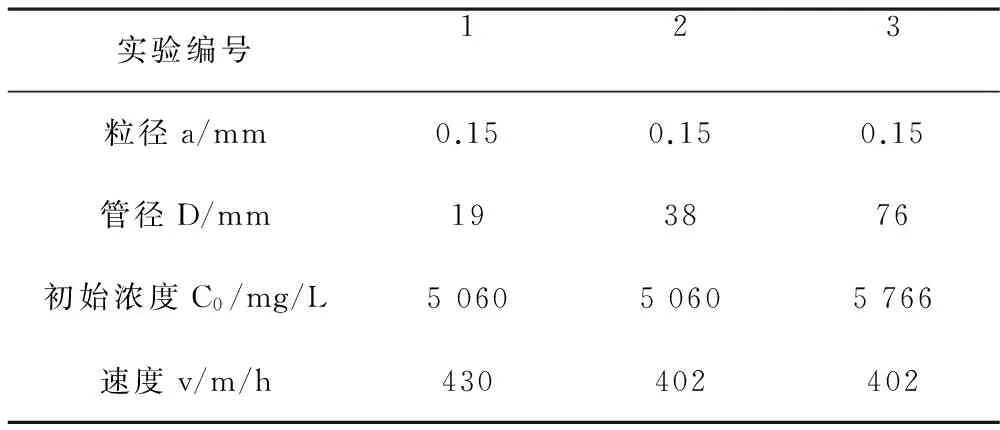
实验编号123粒径a/mm0.150.150.15管径D/mm193876初始浓度C0/mg/L506050605766速度v/m/h430402402

2.1.2 管道悬浮物运移数值模拟

根据实验装置及实验参数设定，用FEFLOW软件建立管道实验模型。模型示意图如图2所示，选择管径19 mm、管长20 m的模型，采用三角形网格剖分，共10 000个网格，设置与实验对应的10个观测点(每隔2 m一个)。

图2 管道数值模型示意图

在管道左端设置与实验相同定浓度，流速通过水头和渗透系数控制，管道管径和长度、模拟时间均与实验一致。调试FEFLOW溶质运移模型吸附系数[10]，将FEFLOW模型计算结果与每个观测点的悬浮物浓度观测数据进行拟合，得出10个与实验观测点浓度对应的吸附系数。类似地，调试沉降系数，拟合一维河流稳态模型计算结果与实验观测结果，得到对应的沉降系数。

2.1.3 实验结果

在尽量保持初始浓度、速度、粒径相同条件下，实验初步探究了管径对沉降系数和吸附系数的影响，得出：管径与沉降系数和吸附系数成反比，沉降系数和吸附系数与运移距离无关。

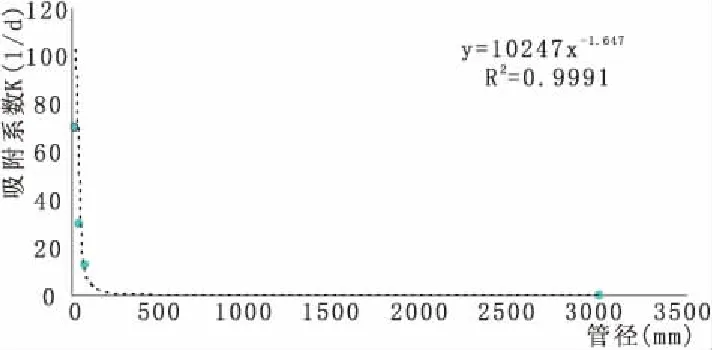
图3 实例条件下沉降系数与管径的对应关系图

2.2 野外实例中管道悬浮物运移等参替代关系构建

实验得出同种条件下吸附系数、沉降系数与距离无关，且得到三组不同管径对应的吸附系数和沉降系数。另外，根据岩溶地区另一个排泥库发生的事故泥浆泄露资料求得的沉降系数为8.14×10-3(1/d)，根据FEFLOW模型模拟结果得到对应吸附系数为0.08。而该排泥库与论文研究的排泥库相比主要是暗河管道大小不同，因此将三组室内得到的沉降系数和吸附系数取结合另一排泥库泄露时求得的对应数据，统计得到沉降系数与管径的对应关系图(见图3)，以及吸附系数与管径的对应关系(见图4)。

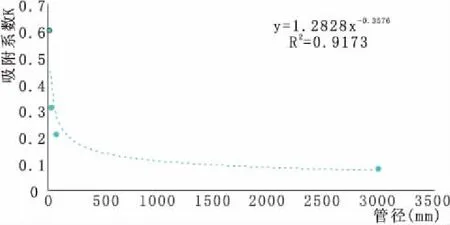
图4 实例条件下吸附系数与管径对应关系

根据实际勘查资料，实例中地下岩溶管道约为5 m宽，外延图3和图4所得的关系，或代入图中拟合公式，得实例沉降系数值为8.29×10-3(1/d)，对应的吸附系数值为0.060 8。

3 岩溶管道等参替代数值模拟方法应用实例

3.1 排泥库工程概况

排泥库位于广西靖西县，本区断裂构造发育，北西向断层遍及全区，其中右江大断裂F1规模最大，为控相区域性断裂，把靖西～田东隆起带错移20多 km。根据野外岩溶水点调查及区域水文地质资料分析，该区域地下暗河管道发育非常强烈，有庞凌(凌晚)地下河和鹅泉地下河两个岩溶水补迳排系统，庞凌地下河与鹅泉地下河两个地下河系统之间存在北西—南东向，次一级地下水分水岭。

鹅泉地下河由1条主干支流和北面3条支流、南面1条支流构成，补给面积为258 km2。地下河系沿岩溶管道、裂隙径流，主干流程约21 km。 拟建排泥库位于鹅泉地下河系统范围内，距鹅泉河干流约2.3 km。

图5 模型3D示意图

3.2 基于FEFLOW的悬浮物运移数值模拟

正确可信的水流模型是溶质运移模型的前提和基础，对水流模型进行识别验证。

3.2.1 水流模拟模型求解及识别验证

根据研究区地质及水文地质勘察资料、示踪试验、钻孔等资料分析污染物泥浆运移的主要途径，确定模拟计算区范围为一相对独立的水文地质单元，西至F1断裂为边界，北至次一级地下水分水岭，南边界和东边界为鹅泉地下暗河，面积约76 m2。模型示意图如图5所示。模型采用三角形单元网格剖分，研究区的总面积为76 km2，在地下暗河及支流处加密网格，

最小的网格面积为35 m2，最大为30 600 m2。在垂向上剖分为2层。研究区总计20 412个网格，16 218个节点。

根据岩性出露情况、岩层及地下暗河分布情况，将渗透系数(Kxx、Kyy)划分为5个分区，岩性分区如图6所示，对应参数见表2。

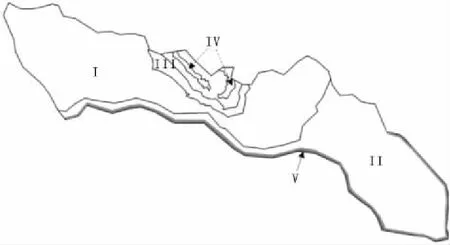
图6 渗透系数(Kxx、Kyy)分区图

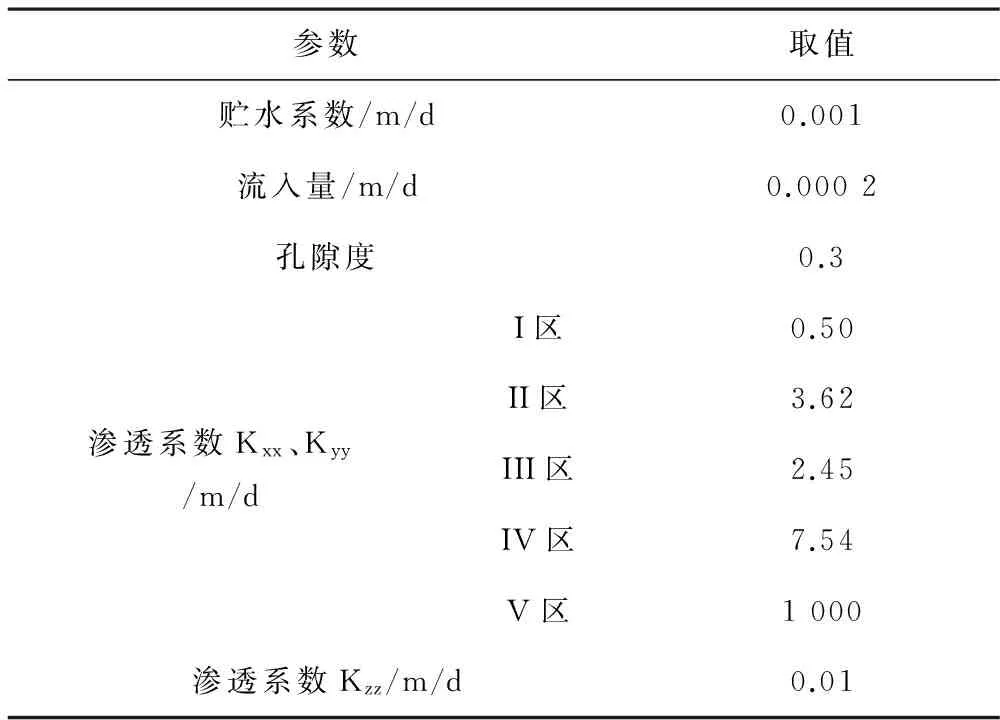
参数取值贮水系数/m/d0.001流入量/m/d0.0002孔隙度0.3渗透系数Kxx、Kyy/m/dI区0.50II区3.62III区2.45IV区7.54V区1000渗透系数Kzz/m/d0.01

模型识别验证期从2014年3月至2015年3月，划分为12个模拟时段，为与丰平枯三期的实测资料相对应，时间步长为20～40d不等。应用试估-校正法和单纯形法识别得到模型参数(表)，所有时段水头拟合误差绝对值的均值在4.36 m以内，考虑到岩溶地水文地质条件的复杂性以及局部峰丛和溶洞对水流的影响，局部水位在现有条件下会有较大出入，但总体水位与实测情况吻合。

3.2.2 基于FEFLOW悬浮物运移数值预测

污染物迁移模拟模型用于预测评价污染物在岩溶管道(地下暗河)的运移情况，岩溶管道弥散度参数参考前人在岩溶管道进行的相关野外试验研究成果，纵向弥散度取值为400 m。污染泄露方式、浓度、等参替代模拟模型计算悬浮物运移距离结果见表3。

3.3 悬浮物迁移预测结果分析

根据预测结果，基于FEFLOW的数值模拟结果总体略大于一维稳态水质模型解析法的结果，枯水期相差约500～800 m，丰水期相差约1 200～1 800 m左右。通过进一步分析，解析法公式中，污染物浓度的影响因素只考虑初始浓度、流速、沉降系数三因素，不考虑水流的源汇项，且流速敏感性高于初始浓度的敏感性；而FEFLOW有限元法在考虑上述三项因素基础上，考虑了河流与地下水之间的水力交换而产生的源汇项，因此悬浮物运移距离稍大，与实际条件更为接近，亦更合理。

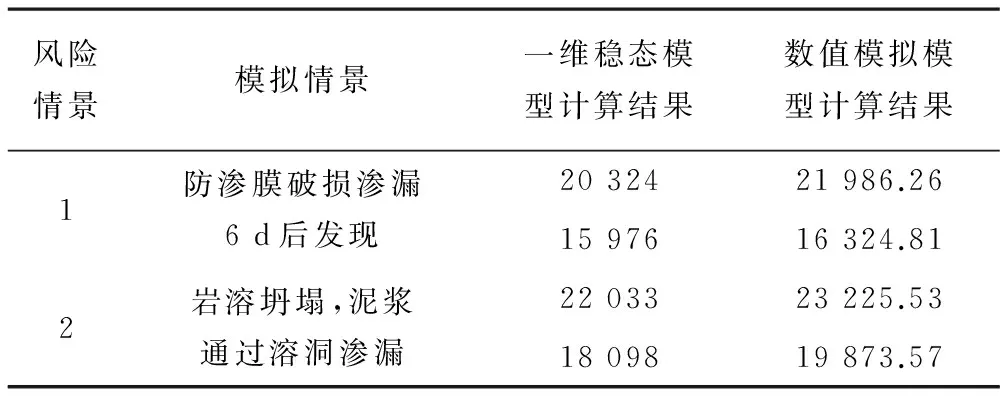
表3 泥浆悬浮物运移距离计算结果一览表 m

注：影响距离为泥浆浓度降至30 mg/L(根据铝工业污染物排放标准GB 25465-2010水污染悬浮物限制为30 mg/L)的范围。

4 结语

(1)FEFLOW模拟岩溶管道中悬浮类污染物迁移时，可以采用机理相似的吸附系数等效替代悬浮污染物运移过程中的沉降系数。

(2)相比于常用的一维稳态水质模型，等参替代模型考虑了岩溶管道与周围裂隙地下水之间的水力交换，模拟岩溶管道悬浮污染物运移更为合理。

(3)影响溶质运移沉降作用的因素有很多，本文所探究的数值法模型采用的吸附系数和解析法参数沉降系数间的对应关系仅是大量算例条件下得出，需要通过试验和野外实际算例的进一步研究和验证。

[1]Shuster, E.T. and W.B. White, Seasonal fluctuations in the chemistry of lime-stone springs: A possible means for characterizing carbonate aquifers. Journal of Hydrology, 1971. 14(2): p. 93-128.

[2]Abusaada M, Sauter M. Studying the flow dynamics of a karst aquifer system with an equivalent porous medium model[J]. Groundwater, 2013.51(4): 641-650.

Fleury P, Plagnes V, Bakalowicz M. Modelling of the functioning of karst aquifers with a reservoir model: Application to Fontaine de Vaucluse (South of France)[J]. Journal of hydrology, 2007, 345(1): 38-49.

[3]Atkinson T C. Present and future directions in karst hydrogeology[J]. Annales de la Société géologique de Belgique, 1985.

[4]Quinlan J F, Ewers R O. Ground water flow in limestone terranes: Strategy rationale and procedure for reliable, efficient monitoring of ground water quality in karst areas[C]//Proceedings of the Fifth National Symposium and Exposition on Aquifer Restoration and Ground Water Monitoring May 21-24, 1985.The Fawcett Center, Columbus, Ohio. 1985. p 197-234, 12 fig, 100 ref. 1985.

[5]Scanlon, B.R., et al., Can we simulate regional groundwater flow in a karst system using equivalent porous media models Case study, Barton Springs Edwards aquifer, USA. Journal of Hydrology, 2003. 276(1-4): p. 137-158.

[6]薛禹群，吴吉春.地下水数值模拟在我国——回顾与展望. 水文地质工程地质.1997. 24(4): 21-24.

[7]郝芳华, 李春晖, 赵彦伟. 流域水质模型与模拟[J]. 北京师范大学出版社.2008.

[8]薛禹群，与春红.地下水数值模拟. 科学出版社.2007.

[9]Karickhoff, S.W., D.S. Brown and T.A. Scott, Sorption of hydrophobic pollutants on natural sediments. Water research, 1979. 13(3): p. 241-248.

[10]张志强，等.基于示踪试验的岩溶管道及水力参数定量解析.人民长江.2015. 46(11): 80-83.

StudyonnumericalmodelofsuspendedsedimenttransportandequalparametersubstitutioninKarstpipelines——taking the prediction of suspended sediment transport in a row of mud banks in Guangxi as an example

ZHOUYu-chao1，ZHUXiao-bin1，WUJi-chun1，WUJian-feng1，ZENGXian-kui1，GUOFei2

(1.Key Laboratory of supergene geochemistry, Ministry of Education/ School of Earth Science and engineering, Nanjing University, Department of Water Science, Nanjing,Jiangsu,210023；2.Key Laboratory of virtual geographic environment, Ministry of education, Nanjing Normal University,Nanjing,Jiangsu,210046)

The migration of karst underground river in the area of suspension simulation is always difficult. In practical applications, due to the role of traditional settlement numerical model without suspension parameters of the reaction, usually only consider the generalization of suspended particles in the underground river in the river by using one-dimensional water quality prediction model, the lack of other methods for effective verification. This paper combines experiment and numerical simulation, laboratory experiments on the transport of suspended solids in pipes under different diameters and initial concentrations are designed, the feasibility of the equivalent substitute of the one-dimensional steady-state water quality model settlement coefficient in a numerical model with similar preliminary investigation mechanism is presented,coupled with mud in guangxi karst area library engineering build specific adsorption coefficient and subsidence coefficient under the condition of isoparametric alternative relations, finally the isoparametric alternative numerical model used in the karst area rivers suspended solids transport simulation, the numerical results show that the numerical model with equivalent parameters is more reasonable than one-dimensional steady-state water quality model. This study enriches the suspension of karst underground river transport simulation method.

Karst；one-dimensional steady water quality model；numerical simulation model；adsorption coefficient；sedimentation coefficient

P641.2

A

1004-1184(2017)05-0003-04

2017-06-17

国家自然科学基金项目(U1503282，41372235，41571386)；国家重点研发计划课题(2016YFC0402807)

周宇超(1991-)，女，江苏江阴人，在读硕士研究生，主攻方向：地下水数值模拟及环境研究。

祝晓彬(1980-)，男，安徽东至人，副教授，主要从事水循环和地下水环境方面教学及研究工作。