非极限状态下有限土体土压力计算方法探究

，，，

(中国地质大学(武汉) 工程学院，武汉 430074)

非极限状态下有限土体土压力计算方法探究

赵轩，马淑芝，唐为民，丰丛杰

(中国地质大学(武汉) 工程学院，武汉 430074)

2017,34(12):89-93

基坑工程中有限土体土压力的计算问题因支护结构的位移控制比较严格,需要考虑非极限状态土压力理论，而以往的研究大多是关于砂性有限土体在非极限状态下土压力理论的探讨，且相关计算方法仍然是基于传统的朗肯土压力理论，事实上对于不满足半无限边界条件的有限土体，朗肯土压力理论是不适用的。对于不满足半无限边界条件的黏性土有限土体，在已有研究的基础上，对墙后梯形滑动楔形土体进行分块处理;采用水平薄层法分别对其进行分析，并考虑黏性土体内摩擦角和黏聚力发挥值以及墙土之间外摩擦角和黏聚力发挥值与位移的关系，构建在非极限状态下黏性土有限土体土压力强度的微分方程;再通过推导得出黏性土有限土体在非极限状态下的土压力强度计算公式。与实际算例实测结果对比分析表明:自填土表面至基坑一定深度范围内，计算值较实测值偏大；而在一定深度以下范围内，计算值与朗肯土压力计算值差异明显，而与实测值的符合程度较好。综合来看，所提出方法是合理可行的，可供相关设计参考。

有限土体；非极限状态；内摩擦角；黏聚力；土压力

1 研究进展

随着城市建筑用地越发紧张，不少建设工程不断向地下空间发展，在城市商业区有大量建设工程拟开挖基坑距离与已有建筑物非常近，因而在已有建筑物地下室墙体与拟开挖基坑间形成宽度有限的土体，如图1(a)所示，此时作用在拟建基坑围护结构上的土压力就属于有限土体土压力范畴。以往对这部分土体土压力的计算仍采用经典朗肯土压力理论，其计算值较实际值偏大，基坑支护结果偏于安全；然而当有限土体宽度b、基坑深度H以及土体内摩擦角φ满足式(1)时，土体潜在剪切滑移面会切割拟开挖基坑相邻建筑物的基础而无法延伸至地面，如图1(b)中虚线所示，此时因有限土体不满足半无限边界条件，若仍采用传统朗肯土压力模式来计算围护结构上的土压力，其计算结果必然存在误差，从而造成基坑支护设计方案不甚合理。因此对不满足半无限边界条件的有限土体土压力计算理论的探讨就显得非常有必要。

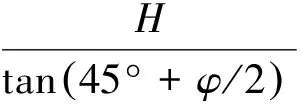
(1)

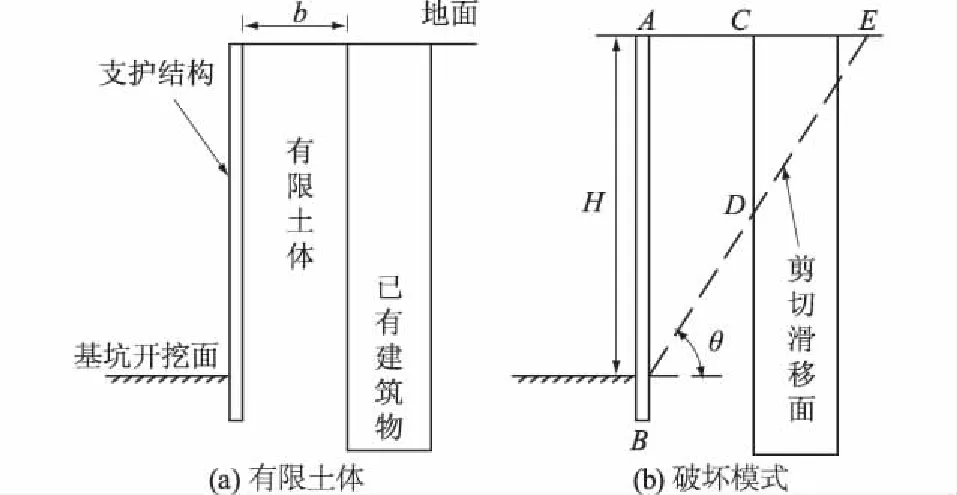
图1 有限土体及其破坏模式

对于不满足半无限边界条件的有限土体土压力计算问题，很多学者进行了初步的研究，亦取得了一定的研究成果。高印立[1-2]、王文杰等[3]、李峰等[4]、马平等[5]、王洪亮等[6]、周子舟[7]均进行了探索尝试，通过适当假设与简化，各自提出了相应的有限土体土压力公式。但是上述研究均是在极限状态下有限土体土压力的计算探讨，而在实际情况中，基坑工程对围护结构的位移控制得比较严格，一般情况下围护结构后面土体变形难以达到极限状态时的位移量，因而探讨非极限状态下不满足半无限边界条件的有限土体土压力计算方法才与实际情况相符。

对于非极限状态下的土压力计算探讨，已有研究通常是对半无限边界土体的探讨，针对不满足半无限边界条件的土体的探讨较少。大多学者均是采用以非极限状态下的土体内摩擦角替换经典土压力理论中的土体极限摩擦角的方法来进行相关探讨研究，并取得了一定的突破，此时求解非极限状态下土体内摩擦角的值是关键。常明方[8]、梅国雄等[9]、施建勇等[10]、黄斌等[11]、卢坤林等[12]、徐日庆等[13]通过适当假设或相关试验，各自从不同角度出发提出了考虑非极限变形情况下的土体内摩擦角或土压力公式。然而，上述方法都只是对在非极限状态下满足半无限边界条件的挡土墙后土体土压力的探讨，对于不满足半无限边界条件的有限土体的研究涉猎甚少。

笔者在徐日庆等[13]研究基础上，将其建立黏性土内摩擦角和黏聚力与位移的关系这一思路运用于有限土体，将有限土体划分为2小块土体，分别采用水平分层法进行受力分析，推导不满足半无限边界条件的黏性土有限土体在非极限状态下的土压力计算公式，并与实际算例的实测结果对比分析，验证该方法的准确性和合理性。

2 抗剪强度参数与位移的关系

2.1 摩擦角与位移关系

对于土体内摩擦角φ，当挡土墙墙体背离土体作小变形移动使得墙后土体并未达到极限状态而是处于非极限状态时，其值在这一变形过程中是逐渐发挥的，并未达到极限值，而是处于初始值和极限值之间的某个值[14]。黄斌等[11]、卢坤林等[12]利用三轴试验推导了无黏性土内摩擦角随位移变化的关系；徐日庆等[13]在黄斌、卢坤林等人的研究基础上推导出黏性土内摩擦角与位移间的关系。此处采用徐日庆提出的公式,即

sinφm=[(1-Ra+ηRa)(1+sinφ)(1-K0)+ηsinφ(1+K0)-η(1-K0)]/[(1-Ra+ηRa)(1+sinφ)(1+K0)-ηsinφ(1+K0)+η(1-K0)] 。

(2)

式中：φ,φm分别为土体内摩擦角极限值和发挥值；K0为初始侧向压力系数；Ra为破坏比，取值一般为0.75～1.0；η为非极限状态与极限状态时的径向应变比值，事实上η可以视为墙体水平位移值S(z)与达到主动极限状态所需位移值Sa的比值，即有η=S(z)/Sa。

对于黏性土，在正常固结情况下,初始侧向压力系数K0=0.95-sinφ。由式(2)可知，土体内摩擦角的发挥值φm仅与土体内摩擦角的极限值φ以及反映位移关系影响的η值有关。图2为土体内摩擦角的发挥值与η关系曲线。

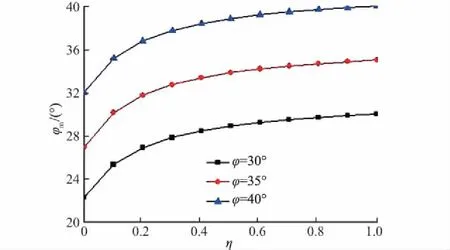
图2 不同φ值时内摩擦角发挥值与η关系曲线

而对于墙土之间外摩擦角δ及其发挥值δm的取值，一些学者给出了不同的表达式[15-16]，此处结合杨位洸[16]的结论，在某一位移值时的墙土接触面外摩擦角发挥值δm取值为

δm=2φm/3 。

(3)

2.2 黏聚力与位移关系

有关土体黏聚力c及其发挥值cm随位移的变化关系的研究较少，主要是缘于黏性土抗剪强度机理的复杂性以及很难精确测定土体黏聚力的数值。杨泰华等[17]归纳总结前人研究成果提出土体黏聚力发挥值cm随着位移在0～c之间线性增加这一观点。而关于墙土之间的黏聚力cw及其发挥值cwm的研究资料也就更少，一般而言取cw=2c/3[18]。本文假定土体黏聚力发挥值cm和墙土之间的黏聚力发挥值cwm随位移具有相同的变化规律，并依徐日庆等[13]的推导结论，土体黏聚力发挥值cm和墙土间黏聚力发挥值cwm的取值分别为：

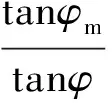
(4)

cwm=2cm/3 。

(5)

式(2)—式(5)即为土体内摩擦角发挥值、墙土间外摩擦角发挥值、土体黏聚力发挥值和墙土间黏聚力发挥值随位移的关系式。由此可知，土体内摩擦角发挥值φm是关键，其余3个量均由它推导得出。如此便建立了抗剪强度参数与位移的关系式。

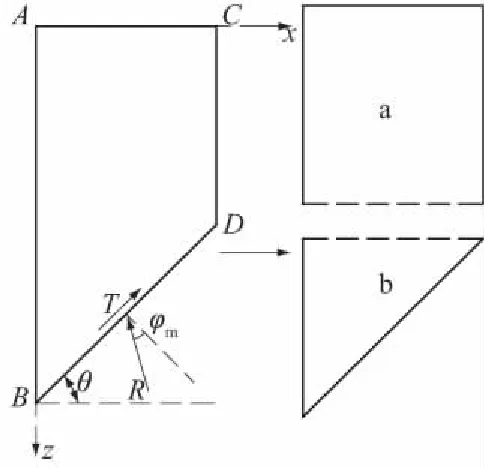
图3 有限土体分解示意图

3 非极限状态土压力计算模式

考虑非极限状态下不满足半无限边界条件的黏性土有限土体土压力计算理论，对于挡墙后梯形滑动土体ABDC，将其划分成如图3所示的2块土体，即矩形区域a与三角形区域b，采用水平薄层法分别对其进行受力分析。

对图3中区域a进行受力分析，在一定深度内取厚度为dz的薄层单元，其受力分析如图4(a)所示。

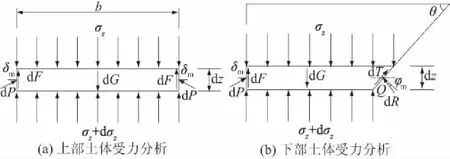
图4 土体薄层单元受力分析

图4中dF为墙土之间的黏聚力，dP为约束土体的墙体对滑动块体的反作用力，其值的大小包含了垂直于墙土接触面的支持力和平行于墙土接触面的摩擦力，作用力的方向则取决于墙土之间外摩擦角的发挥值δm的值。此时薄层单元土体自重dG=γbdz，墙土间的黏聚力dF=cwmdz，墙体对滑动土体反作用力dP的竖直分量为dPv=pdzsinδm。

根据竖直方向上薄层单元受力平衡条件有

σzb+dG-(σz+dσz)b-2(dF+dPv)=0 。

(6)

此时为简化计算，仍假定p=K0σz成立，各物理量代入式(6)后，可得

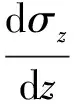
(7)

对式(7)进行积分后得

(8)

再由假定p=K0σz及式(8)可得下式，其中z的范围为0≤z≤H-btanθ。

(9)

同理，对图3中区域b进行受力分析，选取薄层单元dz，其受力分析如图4(b)所示。图中dT为潜在剪切滑移面上土体黏聚力，dR为潜在剪切滑移面下部稳定土体对滑动块体的反作用力，其值大小包含了垂直于潜在剪切滑移面的支持力和平行于潜在剪切滑移面的摩擦力，反作用力的方向则取决于土体内摩擦角发挥值φm的大小。此时，薄层单元土体自重为

dG=γdz(H-z-dz/2)/tanθ。

(10)

墙土之间的黏聚力dF=cwmdz，墙体对滑动土体反作用力dP的水平分量为dPh=pdzcosδm、竖直分量为dPv=pdzsinδm，剪切滑移面下部土体对滑动土块黏聚力dT的水平分量为dTh=cmdz/tanθ、竖直分量为dTv=cmdz。

剪切滑移面下部土体对滑动土块反力dR的水平分量、竖直分量分别为:

dRh=rdzsin(θ-φm)/sinθ;

(11)

dRv=rdzcos(θ-φm)/sinθ。

(12)

根据水平方向和竖直方向上薄层单元受力平衡条件有:

dPh+dTh-dRh=0 ;

(13)

(σz+dσz)(H-z-dz)/tanθ+dPv+dTv+

dF+dRv-dG-σz(H-z)/tanθ=0 。

(14)

再对薄层单元中心线与滑动面交点Q取力矩平衡，则有

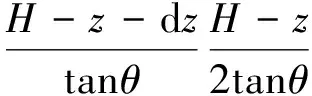
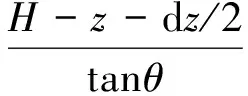
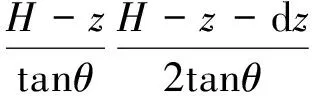
(15)

联立式(13)—式(15)，忽略高阶微分变量，可得：

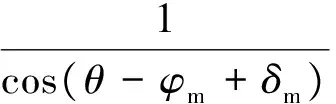
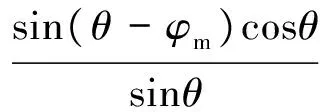
(16)

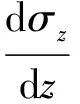
(17)

其中：

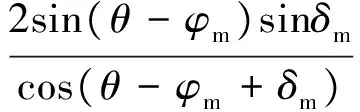
(18)

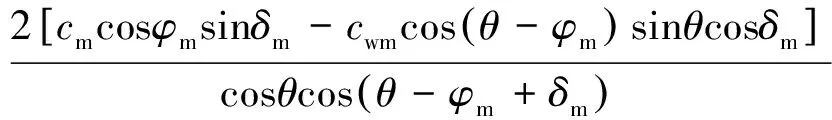
(19)

对式(17)进行积分后得

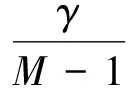
(20)

式中k为积分常数。将式(20)代入式(16)，可得式(21)，其中z的范围为H-btanθ≤z≤H。

(21)

事实上式(9)、式(21)在深度z=H-btanθ处连续，因而可求得积分常数k的取值，再将k值代入式(21)即可得出土压力强度p的确切表达式。

综合上述，式(9)、式(21)即为非极限状态下考虑土体内摩擦角与黏聚力发挥值以及墙土之间外摩擦角与黏聚力发挥值的有限土体土压力强度计算公式。

4 算例分析

武汉市政府对八一路城市次干道进行改造时新建了下穿通道。新建的下穿通道总长814 m，通道基坑最深处约8.4 m，通道泵房基坑深度约12.3 m。通道基坑两侧分布有建筑物、构筑物和市政管线等，且周围建筑物距离开挖基坑较近，由此基坑与已有建筑物之间形成有限土体，宽度大部分是3～5 m，而基坑支护需要保护这些周边环境。在基坑开挖深度范围内，场地地层复杂且成层分布，为方便计算需加权简化处理。此处选取主通道某一断面处进行计算分析，相关基坑计算参数如表1所示。

表1 基坑计算参数

基坑支护结构直立，视为刚性挡墙，支护结构后面填土表面水平，破坏比取Ra=0.85，位移比取η=0.8，剪切破裂角θ=45°+φ/2=50.735°，土体黏聚力和内摩擦角发挥值，墙土之间黏聚力和外摩擦角发挥值均按前述公式进行计算得到。

有限土体宽度b、基坑深度H与破裂角θ满足式(1)，因此经典朗肯土压力理论边界条件不满足。按上述计算方法得到的土压力值与实测值及按朗肯土压力理论计算值绘制成图表，如图5所示。

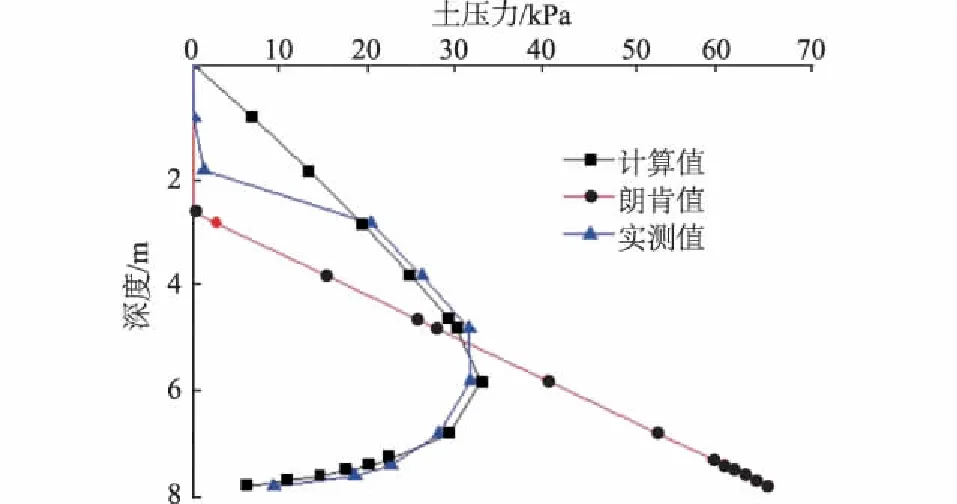
图5 土压力计算值与实测值及朗肯值对比

由图5可知:

(1) 墙后土体土压力计算值自填土表面至临界深度点z=H-btanθ处大致呈线性增加的趋势分布；自临界深度点至基坑底部，墙后土体土压力计算值先仍随深度的增加而增大，但在某一深度处增加到最大值后开始减小。总的来看，土压力计算值的分布在基坑开挖深度上表现出非线性的特点，这与国内外大量研究结论是相吻合的。

(2) 自填土表面至基坑一定深度H0处范围内，土压力实测值近乎于0，而计算值则偏大，反倒是按朗肯土压力理论得到的计算值符合实际；自基坑一定深度H0处至基坑底部范围内，土压力计算值与朗肯土压力计算值相差明显较大，与实测值符合程度较好，这可以表明，一定深度H0值比临界深度z=H-btanθ要小。

(3) 对于黏性土，由经典朗肯主动土压力强度公式Pa=γztan2(45°-φ/2)-2ctan(45°-φ/2)可知，由黏聚力c引起的土压力为负值，会使土体脱离墙，出现一定深度的裂隙，因此这部分土压力可以忽略。而笔者提出公式并未考虑这一裂隙的影响，且对图3中区域a进行分析时，作了p=K0σz的不当假定，这2个因素造成在一定深度范围内，土压力计算值较实测值偏大。至于一定深度范围以下，因黏性有限土体不满足半无限边界条件，经典朗肯土压力值必然会较计算值偏大，同时也较实测值偏大。

5 结 论

(1) 针对有限土体的工程特点，考虑土体内摩擦角和黏聚力的发挥值以及墙土之间黏聚力和外摩擦角发挥值的影响，建立有限土体非极限状态下土压力计算模型，推导出了有限土体土压力强度的计算表达式。

(2) 经与算例计算结果对比分析可知，自填土表面至基坑一定深度范围内，计算值较实测值偏大；而在一定深度以下范围内，基于笔者提出公式的土压力计算值与朗肯土压力计算值相差明显，而与实测值符合程度较好。综合来看，笔者提出方法与实际情况符合较好，说明该方法在一定程度上较为准确合理，可作为一种行之有效的方法供实际工程中求解有限土体土压力。

(3) 在实际算例中对成层土体进行加权处理简化为均质土体，实际情况中土压力随深度分布要更为复杂。再者考虑自填土表面一定深度范围内拉裂隙的影响及有限土体荷化分析的假设条件，这些问题仍有待于进一步研究探讨。

[1] 高印立. 有限土体土压力的计算探讨[J]. 建筑科学,2000,16(5):53-56.

[2] 高印立. 极限分析法计算有限范围土体土压力[J]. 建筑结构,2001,31(8):66-68.

[3] 王文杰,曾进群,陈小丹.深基坑开挖中有限土体土压力计算方法探讨[J].探讨与分析,2004,8(3)30-31.

[4] 李 峰,郭院成. 基坑工程有限土体主动土压力计算分析研究[J]. 建筑科学,2008,24(1):15-18.

[5] 马 平,秦四清,钱海涛. 有限土体主动土压力计算[J].岩石力学与工程学报,2008,27(增1):3070-3074.

[6] 王洪亮, 宋二祥, 宋福渊. 紧邻既有建筑基坑有限土体主动土压力计算方法[J]. 工程力学, 2014,4(31):76-81.

[7] 周子舟. 有限土体主动土压力计算方法的比较[J].工程勘察,2015,(1):20-25.

[8]CHANG M F. Lateral Earth Pressure Behind Rotating Walls [J]. Canadian Geotechnical Journal, 1997，34(2):498-509.

[9] 梅国雄,宰金珉. 考虑位移影响的土压力近似计算方法[J]. 岩土力学,2001,3(22):83-85.

[10] 施建勇,雷国辉,艾英钵,等. 土压力变化规律的应力路径三轴试验研究[J]. 岩土力学,2005,26(11):1700-1704.

[11] 黄 斌,杨 洪,何晓民. 非极限状态主动土压力的研究[J]. 长江科学院院报,2007,24(4):46-49.

[12] 卢坤林,杨 扬. 非极限主动土压力计算方法初探[J]. 岩土力学,2010,31(2):615-619.

[13] 徐日庆,廖 斌,吴 渐,等. 黏性土的非极限主动土压力计算方法研究[J]. 岩土力学,2013,34(1):148-154.

[14] BANG S. Active Earth Pressure Behind Retaining Walls[J]. Journal of Geotechnical Engineering, 1985,111(3):407-412.

[15] 龚 慈,魏 纲,徐日庆. RT模式下刚性挡墙土压力计算方法研究[J]. 岩土力学,2006,27(9):1588-1592.

[16] 杨位洸. 地基及基础[M]. 3版. 北京:中国建筑工业出版社,1997:323-325.

[17] 杨泰华,贺怀建. 考虑位移效应的土压力计算理论[J]. 岩土力学,2010,31(11):3635-3639.

[18] 赵恒惠. 挡土墙后黏性填土的土压力计算[J]. 岩土工程学报,1983,5(1):134-146.

A Computation Method for Earth Pressure of Limited Soilsunder Non-limit State

ZHAO Xuan，MA Shu-zhi，TANG Wei-min，FENG Cong-jie

(Faculty of Engineering, China University of Geosciences, Wuhan 430074, China)

Due to strict control for the displacement of retaining structure in excavation engineering, the theory of soil pressure in non-limit state should be considered in the calculation of soil pressure of limited soils. However, most previous studies were confined to the earth pressure of sandy limited soil under non-limit state, and the calculation methods are based on traditional Rankine’s earth pressure theory which is not applicable in semi-infinite boundary condition. In view of this, for cohesive limited soils which do not meet the semi-infinite boundary conditions, we divided the trapezoidal sliding wedge soil into blocks, and established the differential equation of earth pressure strength of cohesive limited soil at non-limit state according to the curves of mobilized angles of internal friction and external friction and mobilized cohesion vs. displacement angle, respectively. Furthermore, we derived the calculating formula for earth pressure of cohesive limited soils at non-limit state. Calculated values are larger than measured values in the range from soil surface to a certain depth of the pit; while beyond that depth, the calculated values conformed well with measured values but differed greatly from Rankine’s value. In general, the calculation method presented in this paper is reasonable and feasible.

limited soils; non-limit state; internal friction angle; cohesion; earth pressure

2016-08-25；

2016-10-16

赵 轩(1990-)，男，湖北监利人，硕士研究生，主要从事工程地质和岩土工程方面的研究工作,(电话)18108626196(电子信箱)cug050101_21@163.com。

马淑芝(1974-)，女，湖北武汉人,教授，博士，主要从事岩土工程、地质工程专业的教学与科研工作,(电话)13387652308(电子信箱)maszyy@163.com。

10.11988/ckyyb.20160872

TU432

A

1001-5485(2017)12-0089-05

(编辑：王 慰)