粒子群算法优化BP在降雨空间插值中的应用

，，,b

(四川大学 a.水利水电学院； b.水力学与山区河流开发保护国家重点实验室，成都 610065)

粒子群算法优化BP在降雨空间插值中的应用

邱云翔a，张潇潇a，刘国东a,b

(四川大学 a.水利水电学院； b.水力学与山区河流开发保护国家重点实验室，成都 610065)

2017,34(12):28-32

为更好地表达降雨量的空间分布，将粒子群算法(PSO)优化后的反向传输(BP)神经网络分别运用于三峡区间流域日、月和年降雨量的空间插值中，并与单纯BP神经网络和克里金的插值效果作对比。研究结果表明：在日和年的时间尺度上，PSO-BP插值性能较BP有明显改善，且优于克里金的插值效果；在月时间尺度上，PSO-BP插值效果与BP接近且优于克里金。因此，PSO-BP能较好地揭示降雨量在空间的分布规律，也具备在不同时间尺度上对降雨量进行空间插值的能力，是一种较优的降雨空间插值方法。

粒子群算法；BP神经网络；优化；克里金插值；降雨插值

1 研究背景

降雨是与人类密切相关的天气现象，人类赖以生存的水生态环境以及农作物生长，都离不开降雨的作用，在威胁人类生存的洪涝旱灾、泥石流、堤口溃坝等自然灾害事件中，降雨的影响与破坏如影随形[1]。因此，只有清楚降雨的空间分布状况，才能充分利用水资源，加强自然灾害防治，合理安排农业生产[2]。由于技术、地形、经济等条件的限制，地面雨量站的布设无法做到区域全覆盖，致使大部分区域空间降雨数据无法直接获取[3]。因此，降雨量空间插值研究对于掌握降雨量的空间分布特征、满足水资源管理具有重要意义。

传统的降雨空间插值方法包括确定性插值方法(如反距离加权法、泰森多边形法、线性回归法)、地统计插值方法(如克里金、残差克里金法)[4]。上述方法均无法准确描述影响降雨量的关键因子和降雨量之间复杂的非线性关系。由于人工神经网络能有效地揭示变量间的非线性关系,并具备对未知样点降雨量的预测能力。因此，越来越多的国内外学者将人工神经网络方法应用于降雨空间插值研究中。Piazza等[5]选择雨量站的经度、纬度、高程作输入变量，降雨量作输出变量，用以构建多层感知器(MLP)人工神经网络，分别对意大利西西里岛的年均降雨量和月均降雨量进行降雨空间插值，并对在MLP人工神经网络预测的基础上引入残差克里金作了进一步探讨。Seo等[6]将回归克里金和MLP人工神经网络残差克里金进行融合，对韩国济州岛年均降雨量进行了空间插值。莫林等[7]采用BP和RBF 2种人工神经网络对云南省进行月平均、年平均的空间降水插值研究。胡广义等[8-9]构建了基于隐含层节点数可调节的BP人工神经网络和基于GABP的降雨空间插值模型，对湖北宜昌地区的某次大到暴雨天气的降雨量分布进行了估算。

上述研究均取得了较理想的效果，进一步丰富了人工神经网络在降雨插值中的应用研究。本文尝试运用粒子群算法(PSO)优化后的BP人工神经网络和单纯BP人工神经网络对三峡区间流域日、月和年降雨量进行空间插值，并与克里金的插值结果进行了对比。

2 研究数据与分析

2.1 研究区概况及数据来源

本文以三峡区间流域为研究对象。三峡区间流域主要指长江干流寸滩水文站和支流乌江武隆水文站到三峡大坝之间的流域，集水面积约为6万km2，全长为658 km，位于106°36′00″E— 110°44′00″E，28°56′00″N—31°44′18″N。

地面雨情信息主要由区间内99个站点提供(包括地面遥测雨量站、报讯站及水文站)。

2.2 数据分析与选取

初步选择经度、纬度、高程、坡度和坡向5个因子作为降雨影响因子。分别将日、月和年降雨量与各地形因子做相关分析，结果显示纬度与降水量相关性最好，经度次之，其余因子相关性较差，各因子与降雨量相关性详见表1。由此最终选择经度、纬度作为降雨量的主要影响因子。

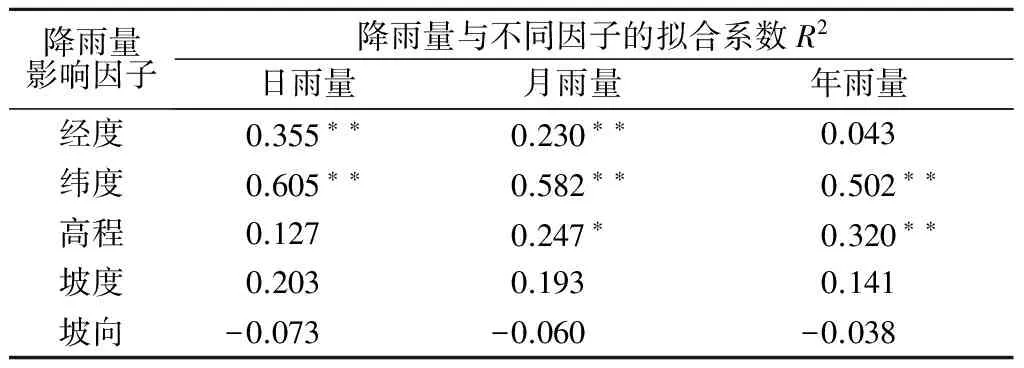
表1 降雨量与各因子的相关性

注：*代表相关性在0.05的水平上是显著的;**代表相关性在0.01的水平上是显著的

在研究区内分别随机选取89个雨量站点和10个雨量站点在2014年8月31日、2014年8月和2014年的降水量数据作降雨插值模型的样本数据及相应的模型检验数据。雨量站点的分布情况见图1。

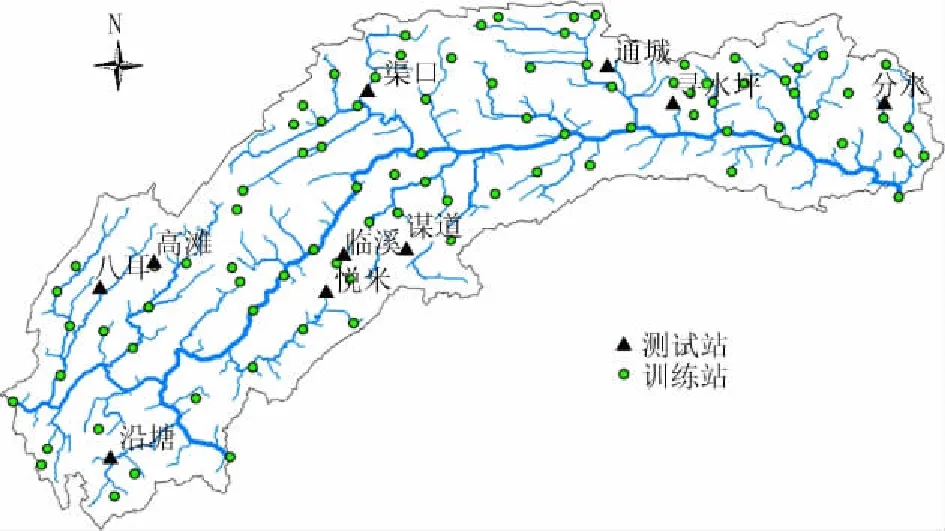
图1 研究区雨量站点空间分布

3 基于PSO-BP的降雨插值模型

3.1 BP神经网络

BP网络的输入层和输出层的神经元数一般根据具体问题确定，隐含层神经元数一般通过经验公式和试算法确定[10-11]。经验公式为

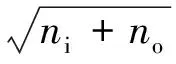
(1)

式中:nh为隐含层神经元数；ni为输入层神经元数；no为输出层神经元数；m为常数,且m∈[1,10]。

运用BP神经网络进行降雨量插值需进行以下几个步骤[12]：

(1) 数据归一化。为消除各维数据量纲或数量级的差异，加快收敛速度，有必要将样本数据统一压缩到一定范围。

(2) 网络初始化。首先确定网络结构，然后给定学习速率、神经元激励函数、训练函数，并完成网络相关参数的设置，最后随机生成连接输入层、隐含层和输出层神经元之间的权值及阈值。

(3) 权阈值更新。反复更新权值和阈值，直至达到预先设定的训练步数或终止条件，训练过程结束。

(4) 预测未知点。用训练好的网络对测试样本中的未知站点进行预测。

3.2 粒子群算法

3.2.1 算法原理

粒子群算法(PSO)最早由Kennedy等[13]于1995年提出，是一种模拟鸟群觅食行为的智能优化算法。算法的具体实现步骤如下：

(1) 完成粒子的数目、问题的求解维度、待求参数的取值空间、飞行速度的限制范围、惯性权重取值、加速度因子取值、最大迭代次数的设置，并在待求参数的取值空间中初始化粒子的位置，在飞行速度的限制范围内初始化粒子的速度，依据适应度函数计算各个粒子对应的初始适应度值。

(2) 寻找或更新当代粒子群中最优适应度值对应的粒子位置(群体极值)和各粒子历代中最优适应度值对应的粒子位置(个体极值)。

(3) 各粒子根据当代群体极值和个体极值首先更新自身速度并对速度进行越界处理，然后更新自身位置后同样进行越界处理，计算更新后的适应度值。速度与位置更新公式分别为

(2)

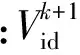
(4) 比较各粒子更新前后的适应度值，若粒子的适应度值更新后变优，则更新群体极值和个体极值。

(5) 判断是否达到预先设置的最大迭代次数，若未达到，则重复步骤(2)—步骤(4)，反之，将最终的群体极值输出作为寻优结果。

3.2.2 参数设置

算法参数设置对求解的质量有着非常重要的影响，一般来说，参数的选取既要参考经验取值也要结合问题需要[14-15]。实际应用时，粒子数目按经验取值，加速度因子的经验取值为c1=c2=2，飞行速度的限制范围和最大迭代次数一般要结合问题需要设置，惯性权重常采用线性递减惯性值，即

ω(k)=ωinitial-(ωinitial-ωfinal)k/Kmax。

(3)

式中:ω(k)为当代惯性权重值；ωinitial为初始惯性权重值，一般取为0.9；ωfinal为终止惯性权重值，一般取为0.4；k为当前迭代次数；Kmax为最大迭代次数。

3.2.3 适应度函数

本研究采用如下适应度函数，即

(4)

式中:f(Pi)为第i个粒子的适应度值；Si,j为在将第i个粒子的位置信息赋到BP神经网络后输入训练样本的第j个信息再经网络训练获得的输出值；Rj为训练样本的第j个期望输出值。不难看出，适应度值越小的粒子，其位置越优。

3.3 PSO-BP降雨插值模型设计

首先，需要对训练样本中实测站点的经度、纬度和降雨量数据进行归一化处理，本文采用的归一化区间为[0.1,0.9][16]。然后确定BP的隐含层神经元数。接着，对BP的网络参数进行预设，学习速率设置为0.01，输入层和隐含层的神经元激励函数分别设置为tansig和logsig函数，目标设置为0.000 1，训练步数设置为500。接着，设置PSO算法的参数，加速度因子c1=c2=2，ωinitial=0.9，ωfinal=0.4，粒子数目、粒子空间位置的限制范围及飞行速度的限制范围需进行相应调试，最大迭代次数则在10～500的经验范围内选取。

在确定了PSO算法参数后，就可以运用PSO算法从粒子空间位置的限制范围中确定出适应度值最优的粒子，然后将该粒子的信息导入BP神经网络作初始的权值和阈值，至此，BP训练前所需的输入信息和网络初始化全部完成。

接下来，BP将按照预设的网络参数要求完成训练过程。训练结束后，网络将具备对未知站点降雨量的预测能力。

4 模型应用

4.1 应用开展

根据式(1)确定的BP隐含层神经元数范围为2～12，粒子数目调试范围按经验取为30～70，最大迭代次数调试范围为10～500，粒子空间位置的限制范围和飞行速度的限制范围按日、月和年降雨插值分别进行调试。通过参数调试可以确定较优的初始的权值和阈值，再对BP神经网络进行500步的训练。为便于将PSO-BP模型与传统BP模型进行对比，采用相同的网络结构对传统BP的训练步数进行调试，调试范围为500～3 000。最后，选择RMSE作为降雨插值结果评判指标，将PSO-BP、传统BP插值结果与克里金插值结果进行对比。RMSE计算公式为

(5)

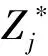
4.2 结果分析

通过对相关参数的反复调试，选取传统BP和PSO-BP在日、月和年降雨空间插值中RMSE值最优的一组参数组合，列于表2和表3。

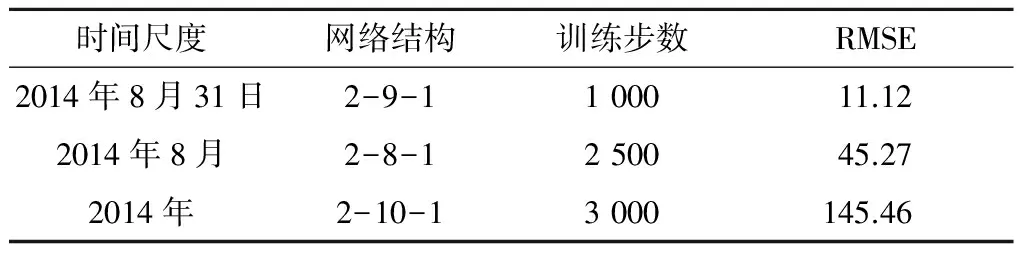
表2 采用传统BP插值的参数组合与RMSE值

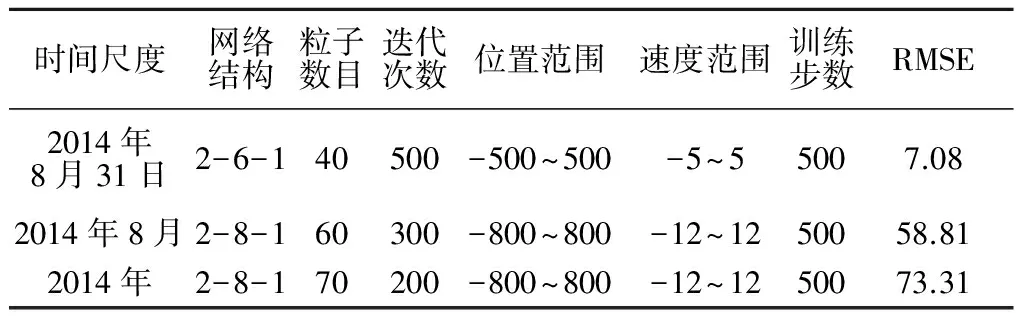
表3 采用PSO-BP插值的参数组合与RMSE值

对比表2和表3可以看出，在月降雨空间插值中，PSO-BP的最优RMSE值为58.81，其插值性能略低于传统BP的45.27。而在日降雨空间插值和年降雨空间插值中，PSO-BP的最优RMSE值分别为7.08和73.31，明显优于传统BP的11.12和145.46。由此可见，通过粒子群算法对BP神经网络初始的权值和阈值进行优选，能为BP的训练提供更好的指导，避免初始的权值和阈值的随机生成，大幅提高稳定性，从而能在较大程度上改善降雨插值效果。此外，利用测试样本中的站点对研究区的降雨空间分布进行克里金插值，计算得到10个测试站点在日、月和年降雨量空间插值的RMSE值分别为13.96,67.80和167.31，显然3种尺度中的PSO-BP插值的最优结果均优于克里金。图2为上述3种方法最优预测值与测试样本中站点的实测值对比情况。

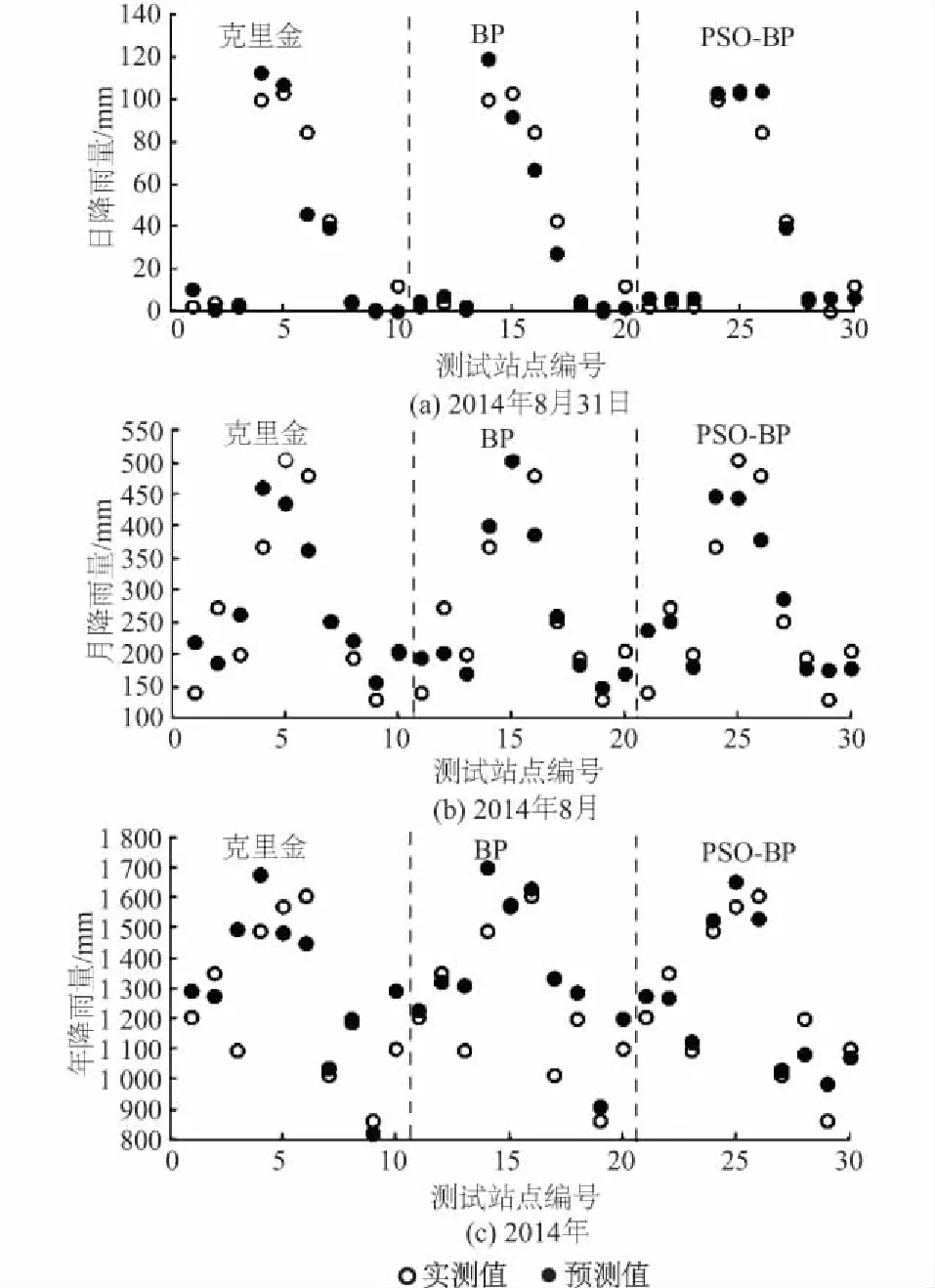
图2 不同时间尺度下3种插值方法最优预测值与实测值

从图2可看出，在日降雨空间插值中，当不同站点的实测降雨量值相差不大时，PSO-BP插值的预测结果表现出的波动更小。当实测降雨量较大时，PSO-BP插值的预测结果也明显优于BP和克里金。在月降雨空间插值中，当实测降雨量较大时，BP的预测结果优于PSO-BP，而PSO-BP则优于克里金。当实测降雨量不大时，3种插值方法的预测结果接近。在年降雨空间插值中，不论实测降雨量大小，PSO-BP的插值性能均明显优于BP和克里金。

综上，PSO-BP从揭示降雨量空间分布内在规律出发，通过优化BP的初始设置，使预测结果更趋于稳定，同样能较好地揭示降雨量在空间的分布规律，也具备在不同时间尺度上对降雨量进行空间插值的能力。

5 结论与讨论

5.1 结 论

(1) 运用粒子群算法优化BP人工神经网络初始的权值和阈值后，能够明显提高BP网络的预测能力。

(2) 将PSO-BP运用到三峡区间流域降水空间插值中时，PSO-BP模型在日和年时间尺度上的最优插值结果的RMSE均小于传统BP神经网络和克里金插值结果的RMSE;在月尺度上，其最优插值结果也比克里金插值更优且接近BP模型。这表明PSO-BP模型降雨空间插值结果较为准确，同时与传统的BP网络相比，PSO-BP模型具有良好的稳定性，能够更好地运用于空间插值中。

5.2 讨 论

降雨插值的方法多种多样，应针对不同研究区域不同时空尺度选取合适的插值方法。当采用PSO-BP插值方法时，应当考虑对PSO的粒子数目、粒子空间位置的限制范围、飞行速度的限制范围、最大迭代次数及BP的训练步数、学习速率等参数进行调试，以期获得较好的效果。另外，增加与降雨量相关性显著的其他变量作为输入变量也能在一定程度上改善插值性能，在BP和PSO-BP模型融入残差克里金插值也可作为一种可供选取的插值方法。

[1] 胡广义．分布式降雨量估算模型与方法研究[D]．武汉：华中科技大学，2009.

[2] 朱 蕾，黄敬峰．山区县域尺度降水量空间插值方法比较[J]．农业工程学报，2007,23(7)：80-85.

[3] 张余庆，陈昌春，姚 鑫,等．江西省信江流域极端降水时空变化特征[J]．水土保持研究，2015，22(4)：189-194，200.

[4] 汤国安，杨 昕,等．地理信息系统空间分析实验教程[M]．2版.北京：科学出版社，2012.

[5] PIAZZA A D, CONTI F L, NOTO L V,etal.Comparative Analysis of Different Techniques for Spatial Interpolation of Rainfall Data to Create a Serially Complete Monthly Time Series of Precipitation for Sicily, Italy[J]. International Journal of Applied Earth Observation and Geoinformation, 2011, 13(3): 396-408.

[6] SEO Y M, KIM S W, VIJAY P. Estimating Spatial Precipitation Using Regression Kriging and Artificial Neural Network Residual Kriging(RKNNRK)Hybrid Approach[J]．Water Resources Management, 2015, 29(7): 2189-2204.

[7] 莫 林，张秋文．人工神经网络在降水量空间插值中的应用研究[J]．计算机与数字工程，2007，35(9)：9-12.

[8] 胡广义，张秋文，张勇传．基于BP人工神经网络的分布式降雨量插值估算[J]．华中科技大学学报(自然科学版)，2009，37(4)：107-110.

[9] 胡广义，张秋文，张勇传．GA优化的BPNN模型在分布式降雨量插值中的应用[J]．武汉大学学报(工学版)，2009，42(4)：466-469.

[10] SETIONO R. On the Solution of the Parity Problem by a Single Hidden Layer Feedforward Neural Network[J]. Neurocomputing, 1997, 16(3): 225-235.

[11] JOU C, YOU S S, CHANG L W．Analysis of Hidden Nodes for Multi-layer Perceptron Neural Networks[J]. Pattern Recognition, 1994, 27(6): 859-864.

[12] 王小川，史 峰，郁 磊． MATLAB神经网络43个案例分析[M] ．北京：北京航空航天大学出版社，2013.

[13] KENNEDY J, EBERHART R. Particle Swarm Optimization[C]∥Proceedings of the 1995 IEEE International Conference on Neural Networks. Perth, Australia, November 27-December 1, 1995: 1942-1948.

[14] SHI Yu-hui, EBERHART R C. Parameter Selection in Particle Swarm Optimization[C]∥Lecture Notes in Computer Science: International Conference on Evolutionary Programming. California, USA, March 25-27, 1998: 591-600.

[15] SHI Y，EBETHART R.C． A modified Particle Swarm Optimizer[C]∥Proceedings of the IEEE Congresson Evolutionary Computation．Piscataway：IEEE，1998:69-73.

[16] IMIRE C E, DURUCAN S, KORRE A. River Flow Prediction Using Artificial Neural Networks: Generalization Beyond the Calibration Range[J]. Journal of Hydrology，2000, 233(1/2/3/4): 138-153.

Application of BP Neural Network Optimized by Particle SwarmOptimization to Rainfall Spatial Interpolation

QIU Yun-xiang1, ZHANG Xiao-xiao1, LIU Guo-dong1,2

(1. College of Water Resource & Hydropower, Sichuan University, Chengdu 610065, China; 2.State Key Laboratory of Hydraulics and Mountain River Engineering, Sichuan University, Chengdu 610065, China)

To better describe the spatial distribution of rainfall, we applied BP neural network optimized by particle swarm optimization to the daily, monthly and yearly rainfall spatial interpolation of the Three Gorges reservoir area, and compared the performance with those of simple BP and Kriging interpolation. We found that in daily and yearly time-scale, PSO-BP neural network performs better than BP and Kriging; while in terms of monthly time-cale, PSO-BP result is close to BP and better than Kriging. We conclude that BP neural network optimized by particle swarm optimization could better reveal the law of spatial distribution of rainfall and has the ability of spatial interpolation in different timescales, and therefore is an excellent method for rainfall spatial interpolation.

particle swarm optimization; BP neural network; optimization; Kriging interpolation; rainfall interpolation

2016-08-19;

2016-10-11

邱云翔(1992-)，男，四川德阳人，硕士研究生，研究方向为水环境资源开发利用与保护，(电话)18728423654(电子信箱)qiuyxsp@163.com。

10.11988/ckyyb.20160837

P332.1

A

1001-5485(2017)12-0028-05

(编辑：王 慰)