基于Spark平台的聚类算法的研究和实现

沈阳理工大学信息科学与工程学院 胡 可 姜学军

基于Spark平台的聚类算法的研究和实现

沈阳理工大学信息科学与工程学院 胡 可 姜学军

传统的聚类算法[1]是从要聚类的样本中任意挑选指定个样本作为中心点开始聚类，中心点选取不同，聚类算法每次执行的结果可能不一样，这样会导致不稳定的结果。为了使聚类结果更加稳定，在聚类算法开始之前怎样得到准确的中心点个数以及正确地挑选合适的初始中心点[2]的研究具有非常重要的价值。Mean shift算法[3]是一种非参数密度估计算法。Mean shift算法可以通过不停的循环调用，可以很快地收敛于概率密度函数最大的地方。算法的过程就是不断寻找概率密度局部最大值的过程。通过Mean shift算法可以很快的找到中心点。

聚类算法；mean shift

1 Mean shift算法概述

假设一个d维空间Rd，其d维空间中有n个数据点xi，i = 1，2，…，n ……随便取其中一点x，那么此时它的多元核密度估计表达式由核函数[4]k(x)和d*d维正对称带宽矩阵构成，该函数可以表示为：

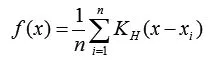
其中KH(x)：

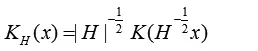
其中，核函数 k(x)决定了采样点与核中心点之间的相似程度。Mean Shift算法变形如公式如下所示。

其中，h为半径，ck,d，nhd为单位密度。

Mean Shift向量表示为：

令mh,G(x)=0，可以求得向量最终坐标：

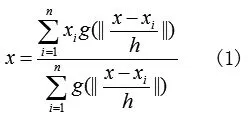
Mean Shift算法流程可以简述为：

1)在d维空间中以x为圆心，以h为半径，做一个高维球，落在球内的所有点为xi。

2)计算 mh,G(x)，手动设向量的值为δ，如果mh,G(x)＜δ，程序结束。

否则mh,G(x)＞δ，则利用公式1) 重复以上步骤直到迭代结束。

2 对聚类算法的改进

2.1 k-中心点聚类算法及缺点

当利用k-中心点算法[5-7]对数据集进行聚类时，首先，人工设定需要聚类数目k，然后随机在样本点内选择k个点作为初始中心点，剩下的n－k个样本点计算样本与k个中心点的距离，将样本点划分到距离最近的中心点所代表的簇。接着在每个簇中计算改簇中所有样本点的均值，选用距离均值最近的样本点作为新的簇中心，重复上述步骤直到该簇的中心点不再发生明显的变化(簇的绝对误差和收敛)为止。簇的绝对误差和反应聚类的质量，值越小，表示类簇越紧凑，聚类效果越好。假设聚类好的k个簇为X1，X2，…，Xk，每个簇的中心点r1，r2……rk，则每个簇的误差和E的公式为：

k-中心点聚类算法对于数据簇内密集、簇间稀疏的情况，其聚类效果较好(误差平方和最小)，但存在因初始点的选取问题而导致不稳定的聚类结果的缺陷[8]。聚类算法的正确率与选择的中心点有很大关系，致使算法相对不稳定，初始点选取的随机性不仅会导致初始点不同时运行效率不一样，更可能使聚类结果不一致，影响算法在实际中的效果。

2.2 Mean Shift算法对k-中心点算法的改进

针对上述k-中心点算法的缺陷，已有很多学者对算法提出了改进[9-10]，但是现有的改进方法实现起来较为复杂，不便于直接在实际问题中应用。直观上，如果一个点附近的邻居点越多，则该点越有可能是簇的中心点。Mean shift 算法[3]是一种非参数密度估计算法。Mean shift算法可以通过不停的循环调用，可以很快地收敛于概率密度函数最大的地方。算法的过程就是不断寻找概率密度局部最大值的过程。通过Mean shift算法可以很快的找到中心点。

使用Mean Shift算法改进k-中心点算法：

输入数据：数据集X（总共包含n个样本）和簇数目k

输出数据：聚好类的k个簇

过程：

步骤1：计算任意两样本点间距离d(xi，xj) ；

步骤2：取样本点间距离的均值的k分之一作为样本点的邻域半径ε；

步骤3：确定初始中心点集合C：

步骤3.1：从X中随机选择一点G，以G为起点，以将此点ε邻域内所有点为终点做一个矢量，求这些矢量和得到mean shift向量，以mean shift向量终点为起点，重复上述动作最终得到密度最大点c1，作为第一个初始聚类中心加入集合C；

步骤3.2：从X中找出距离c1最远的样本按照步骤3.1得到一个初始聚类中心c2，将c2加入集合C；

步骤3.3：从X中找与c1，…，ck－1距离和最远的样本按照步骤3.1得到一个初始聚类中心ck，将ck加入集合C；

步骤4：最后将剩下的n－k个样本点计算样本与集合C中的距离，将样本点划分到距离最近的中心点ci所代表的簇；

步骤5：输出k个簇。

3 实验结果与分析

下面将对K-中心点算法与改进后的聚类算法的聚类效果在不同的应用景进行比较分析。

3.1 分区数与聚类效果分析

每个分区所聚类的个数c如果是指定的聚类数目k的3倍以上效果会更好，这样可以使得所有的子分区不会聚成一个簇。实验结果表明：如果聚类个数c小于聚类数目k时，聚类结果可能与理想的情况不匹配。

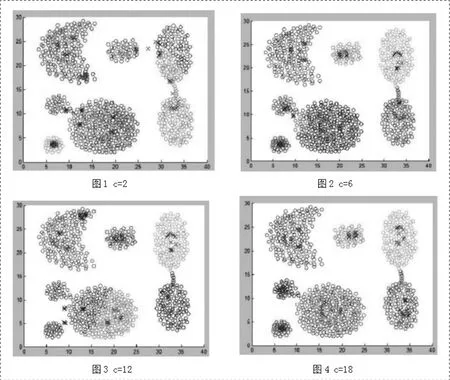
上图说明，在k为6时，c为2、6、12，即小于k的2～3倍，则聚类结果不理想。而在c为18时，聚类结果理想。

3.2 对于K-中心点算法和改进K-中心点算法的比较

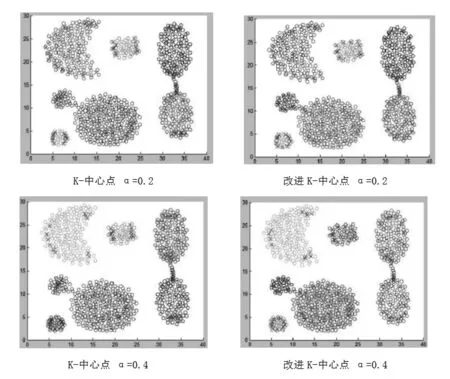
从图中看出在收缩因子α的值为0.2或者0.4时，K-中心点算法的聚类结果与期望情况不符，而使用Mean Shift算法改进的聚类算法的聚类效果相对比较符合情况。因此Mean Shift算法改进的聚类算法在数据处理上比K-中心点算法效果更好。

4 结论

原始的k-中心点算法使用在所有样本点里随机选择k个点作为中心点，这样的方法并没有考虑样本点的实际分布，导致聚类算法的正确率与选择的中心点有很大关系，致使算法相对不稳定，并且结果容易出现局部最优解。而采用Mean Shift算法改进的聚类算法获得初始中心点，使用这种方法得到的初始聚类中心收敛于概率密度局部最大值，与真实的聚类中心分布较为一致，算法稳定且快速收敛，同时也降低了测试的错误率。实验结果证明了我们设计目标。

虽然Mean Shift算法改进的聚类算法稳定性和准确率有所提升，并且由大量数据证明在聚类算法的应用中效果良好，但对于该方法的有效性评估尚处于定性阶段，未来将开展针对此类数据聚类效果的整体、定量评估方法，从而对不同聚类算法进行评价。

[1]周爱武,于亚飞.K-means聚类算法的研究[J].计算机技术与发展,2011(02):2.

[2]汪中,刘贵全,陈恩红.一种优化初始中心点的K-means算法[J].模式识别与人工智能,2009,22(2).

[3]Comaniciu D,Ramesh V,Meer P.Real-time tracking of nonrigid objects using Mean shift[C]//Proc IEEE Coference on Computer Vision and Pattern Recognition,2000:142-149.

[4]CHENG Yi-zong.Mean shift,mode seeking,and clustering[J].IEEE Transactions on Pattern Analysis and Machine Intelligen ce,1995,17(8):790-799.

[5]ESTER M,KRIEGEL H P,SANDER J,et al.A density-based algorithm for discovering clusters in large spatial databases with noise[J].Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining.Portland:AAAI,1996:226-231.

[6]Song Y,Liang J G.Study of fuzzy clustering algorithm using in C RM[J].Logistics Management,2005,28(1):26-28(Ch).

[7]Bradley PS,Fayyad UM.Refining initial points for k-means clustering［DB/ OL].[2014-06-02].http://pub-lic.zirmed.com/wp-content /uploads /2014 /12 /Refining-In-itial-Points-for-k-Means-Clustering.pdf.

[8]Chen J H,Zhang Q,Feng WX,etal.Lightning location system and lightning detection network of China power grid[J].High Voltage Engineering,2008,34(3):425-431(Ch).

[9]Yun Won Chung;Min Young Chung;Dan Keun Sung. Modeling and Analysis of Mobile Terminal Power on/off-State Management Considering User Behavior[J].Vehicular Technology,IEEE Transactio ns.2008,6(57):3708-3722.

[10]Wei-Jen Hsu;Dutta,D.;Helmy,A.Structural Analysis of User Association Patterns in University Campus Wireless LANs[J].Mobile Computing,IEEE Transactions.2012,11(11):1734-1748.