基于粒子群算法的组合模型在变形分析中的应用

王显鹏，黄声享，李冠青

(1.广州市增城区国土资源和规划局,广东 广州 511300；2.武汉大学 测绘学院,湖北 武汉 430079)



基于粒子群算法的组合模型在变形分析中的应用

王显鹏1,2，黄声享2，李冠青2

(1.广州市增城区国土资源和规划局,广东 广州 511300；2.武汉大学 测绘学院,湖北 武汉 430079)

在构建并联组合模型进行变形预测时，单项模型权值的确定是个关键问题。为了提高变形预测的精度，以基坑监测数据为例，采用GM(1,1)模型与ARMA模型进行组合，在拟合误差平方和最小的准则下，使用粒子群算法求解两单项模型的最优权值，进而构建并联组合模型进行变形预测。结果表明，该方法融合各单项模型的优势，可以提高预测精度，避免求解线性规划问题，具有较好的实用性。

粒子群算法；GM(1,1)模型；ARMA模型；组合模型；变形分析

基坑监测可以及时地了解工程状态，为决策者提供事实依据，对确保工程安全具有十分重要的意义。由于受到多种因素的影响[1-2]，使用单一预测模型进行变形分析往往具有一定的局限性，GM(1,1)模型和ARMA模型作为变形预测中常用的两种模型，两者各有优点和不足。将两种方法进行结合构建组合模型，发挥两者的优点，进一步挖掘数据信息，可以有效地降低预测过程中随机因素的影响，提高预测精度[3-4]。

本文简要介绍灰色GM(1,1)模型、ARMA模型和粒子群算法的基本原理，分别运用这两种单项模型对观测序列进行预测，得到相应的模拟值及残差序列，然后在拟合误差的平方和最小的准则下，使用粒子群寻找单项模型的最优权值，以此构建组合模型。

1 原理简介

1.1 GM(1,1)模型

对序列x(1)建立一阶微分方程

(2)

式中：a为发展系数;u称为灰色作用量。用最小二乘法求解得

[a,u]T=(BTB)-1BTyn.

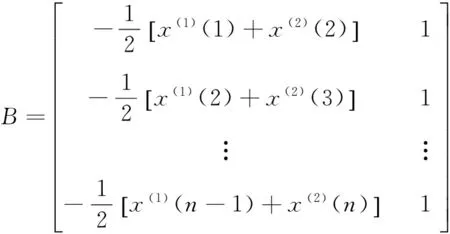
求解微分方程得

通过累减还原，得到x(0)的预测模型为

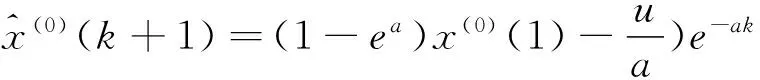
k=1,2,…,n.

(4)

1.2 ARMA模型

若时间序列的数据项Xt可以由该数据项前面的数据项Xt-1,Xt-2,…Xt-m和随机项αt以及前面的随机项αt-1,αt-2,…αt-m线性表示出来[9-11]，即为

Xt=αt+f1Xt-1+f2Xt-2+…+fmXt-m-

称为自回归移动平均模型，记为ARMA(m,n)模型。其中，m为自回归的阶数；n为滑动的阶数。

1.3 粒子群算法

在粒子群算法(PSO)中，每个粒子都被当作目标问题的一个潜在解，粒子以一定的速度向目标逼近，且通过一个目标函数(适应值)来判断每个粒子与目标之间的距离远近[12-15]。距离最近的视为当前的最优粒子，其他所有粒子都将据此追随，经过逐次搜索后得到问题的最优解。每代粒子根据自身及同伴的飞行经验更新自身，也就是追踪两个极值，一是粒子自身经验的最优解Pbest，另一个就是整个种群社会经验的最优解gbest。

假设粒子的搜索空间是N维的，种群中粒子数为m,其中第i个粒子的位置为xi=(xi1,xi2…xiN)，将粒子的位置向量代入适应值函数f(x)计算出其适应值大小，评价粒子位置的优劣，粒子的运动速率为向量vi=(vi1,vi2…viN)，第i个粒子从开始到当前为止的最优位置是Pbest=(pi1,pi2…piN)，整个粒子群从开始到当前为止的最优位置是gbest=(g1,g2…gN)。粒子群算法根据式(6)和式(7)来更新粒子的速度和位置。

vin(t+1)=w*vin(t)+c1φ1*(pin(t)-xin(t))+

vin(t+1)=xin(t)+vin(t+1).

(7)

式中:i=1,2,…，m;n=1,2,…,N，t为当前迭代的代数;vin是第i个粒子的速度第n维分量;xi是第i个粒子的位置第i维分量;w为惯性因子;c1,c2是学习因子;φ1,φ2是0到1之间的随机数，pin代表粒子i个体当前最好位置的第n维分量，gin代表粒种群当前最好位置的第n个分量。

2 粒子群算法的组合模型

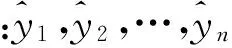
设预测偏差为

组合预测的最优权重求解，是对误差平方和在最小二乘准则下求解如下数学问题：

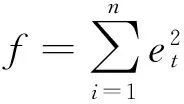
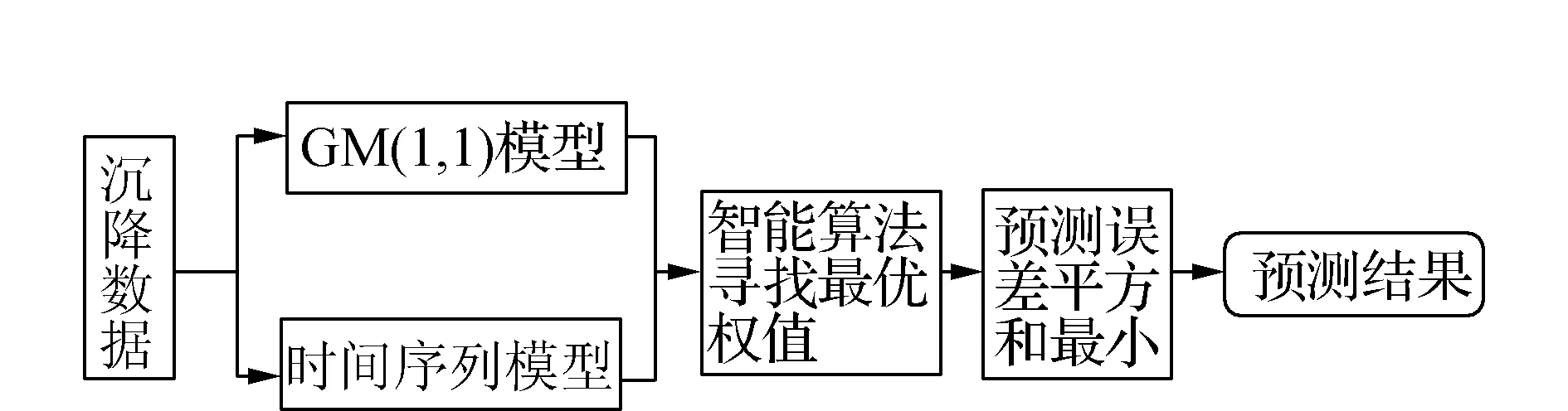
图1 组合模型结构图

3 实例分析

本文以广州某基坑监测项目为例，共有21期沉降数据(见表1)，数据预处理后，对前18期数据分别使用GM(1,1)模型和ARMA模型进行处理，然后采用粒子群算法寻找最优权值，进而构建组合模型对后3期沉降进行预测。

各单项模型处理结果见表1，其中1～18期为模型拟合值，19～21期为预测值。

表1 单项模型处理结果 mm

采用粒子群算法(PSO)进行单项模型权值寻优，初始随机生成30个粒子，进化50次，学习因子c1，c2取1.494 45，惯性权重w取0.7。粒子初始分布位置如图2所示。

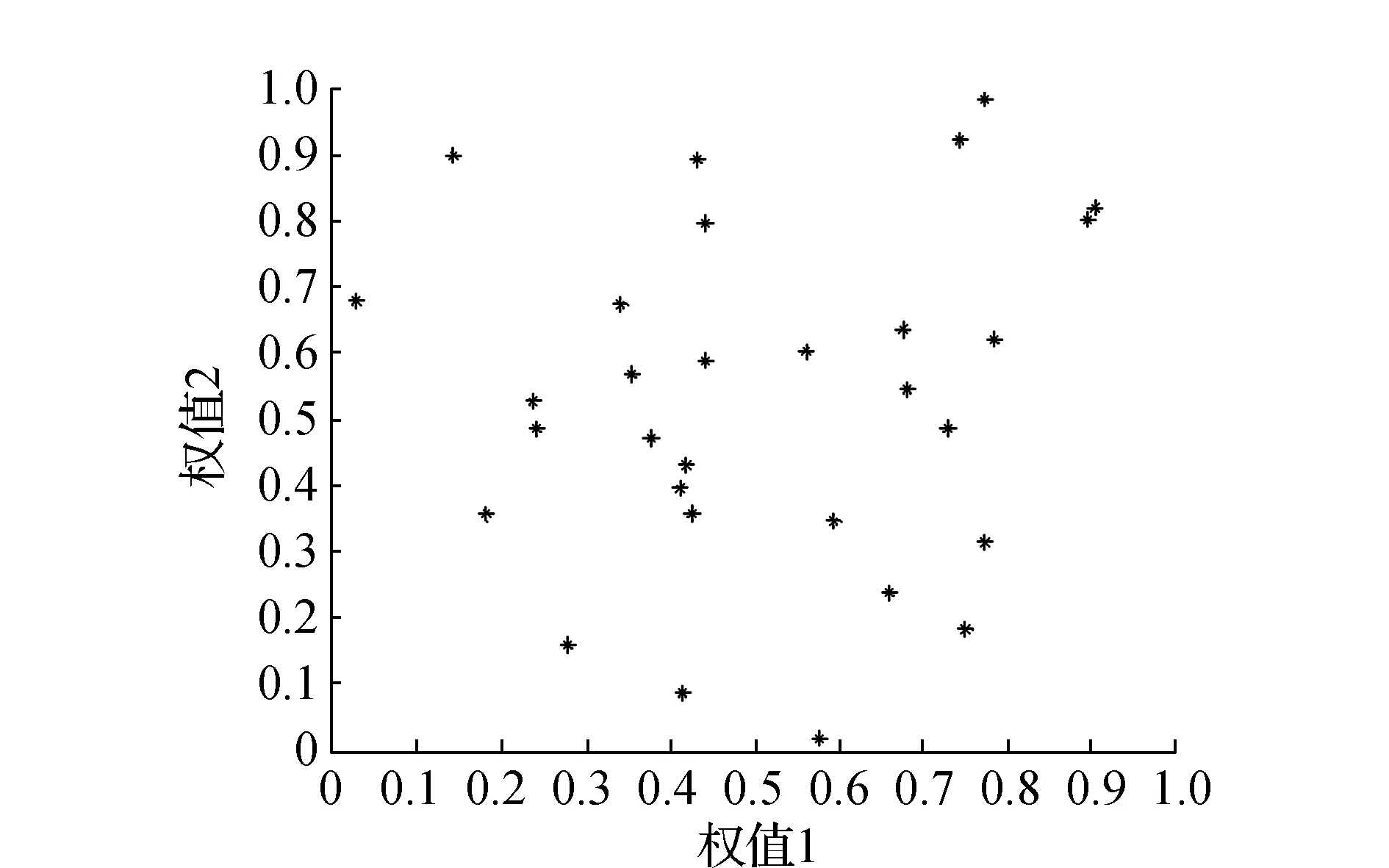
图2 粒子初始位置分布图

由图2可见，粒子初始化后，呈现随机分布特征，经过寻优查找，最优个体适应度值不断下降，下降过程如图3所示。

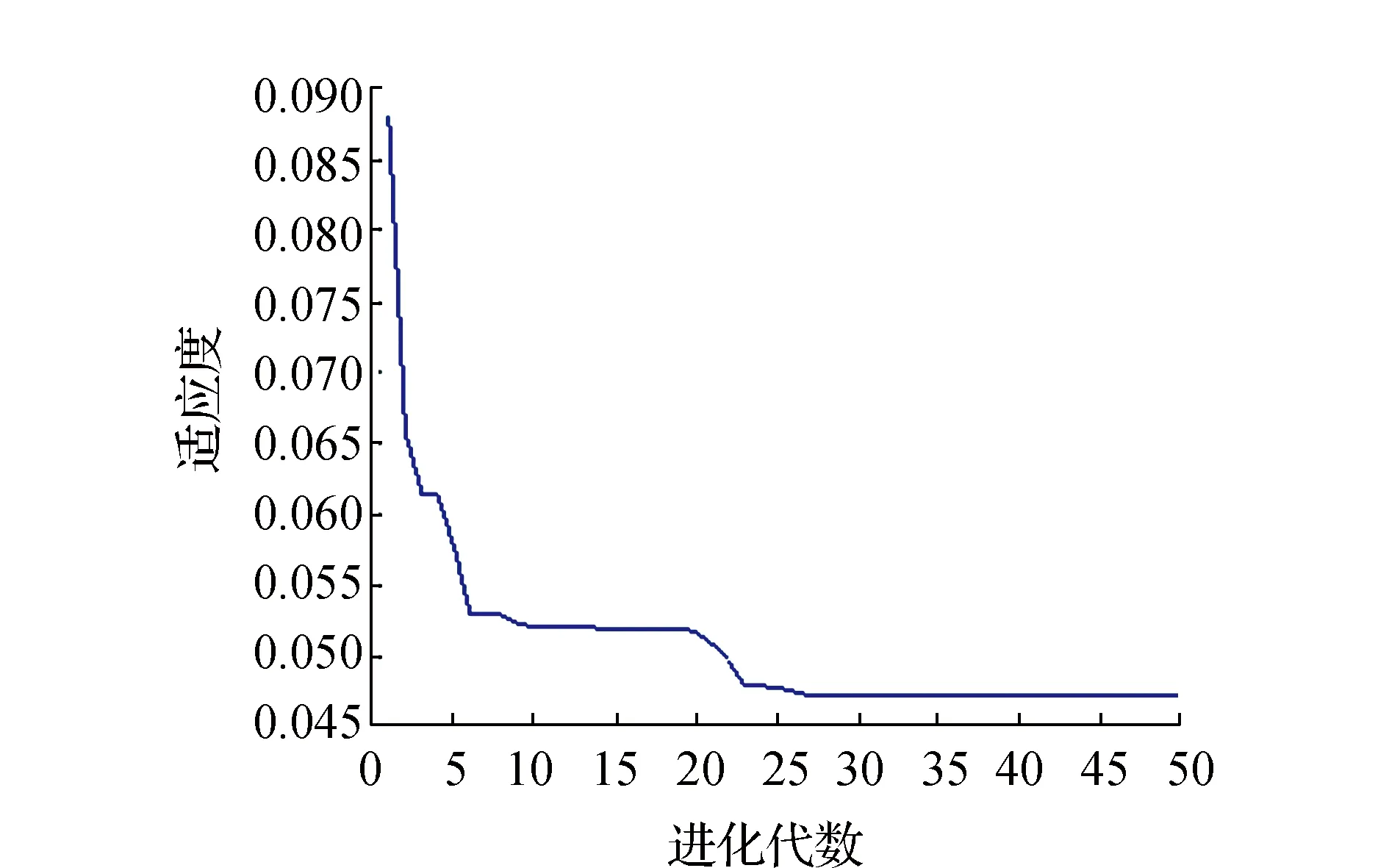
图3 最优个体适应度变化图

寻优后，绝大部分粒子非常靠近最优值，分布位置非常集中，粒子的最终分布位置如图4所示。其中每个粒子所对应的横轴代表的是GM(1,1)模型的权值，纵轴代表的是ARMA模型的权值。

图4 粒子最终分布位置图

经解算，最终寻找到的GM(1,1)模型的组合权值ω1为0.275 7，时序模型的组合权值ω2为0.722 3，故组合模型的表达式为

yt=0.275 7y1+0.722 3y2.

(10)

使用组合模型进行沉降预测，预测结果与单项模型的对比见表2、表3和图5。

表2 模型预测结果对比 mm

表3 预测结果相对误差对比 %

由表3和图5可知，采用粒子群算法进行单项模型权值寻优后，构建的组合模型预测误差小于两种单项模型，获得较高的预测精度，较好地融合灰色GM(1,1)模型和时序ARMA模型的优势。

图5 3种模型预测误差对比

4 结束语

在变形监测数据处理中,不同的单项模型具有各自的优点和不足，将不同的预测模型以恰当的模式构建组合预测模型，可以发挥各单项模型的优势，充分利用观测成果，更好地反映系统的变化规律。本文采用粒子群算法求解组合模型中单项模型的权值，避免求解线性规划问题。结果表明，该方法构建的组合模型实现较好的预测效果，具有一定的实用价值。

[1] 黄声享，尹晖，蒋征.变形监测数据处理[M].2版.武汉:武汉大学出版社,2010.

[2] 单锐，王淑花，高东莲，等.基于时间序列模型与灰色模型的组合预测模型的研究[J].燕山大学学报，2013,36(1)：79-83.

[3] 何书元.应用时间序列分析[M].北京:北京大学出版社，2003：3-20.

[4] 刘燕芳，陈启华，丁林磊.灰色组合模型在变形预测中的应用[J].工程勘察，2013(1)：58-60.

[5] 邓聚龙.灰色系统基本方法[M].武汉：华中理工大学出版社，1987:15-39.

[6] 徐秀杰，黄张裕，刘国超，等.改进的灰色GM-AR组合模型在基坑监测数据处理中的应用[J].测绘与空间地理信息，2015,38(1)：200-203.

[7] 袁豹，岳东杰，李成仁.基于总体最小二乘的改进GM(1,1)模型及其在建筑物沉降预测中的应用[J].测绘工程,2013,22(3):52-55.

[8] 杨富春,黄张裕,贾莹媛,等.基于GM(1,1)灰色模型卫星钟差短期预报的精度分析[J].测绘工程，2012，21(5):25-29.

[9] 刘娜，栾元重，黄晓阳，等.基于时间序列分析的桥梁变形监测预报研究[J].测绘科学，2011，36(6)：46-48.

[10] 张松,田林亚.时间序列分析在地铁沉降监测中的应用[J].测绘工程,2014,23(10):63-66.

[11] 唐争气,谭志强.灰色时序组合模型在基坑监测中的运用[J].测绘工程,2014,23(2):49-53.

[12] 李博.粒子群优化算法及其在神经网络中的应用[D].大连：大连理工大学，2005:3-4.

[13] 李爱国，覃征，鲍复民，等.粒子群优化算法[J]．计算机工程与应用，2002(21):1-3.

[14] 薛婷.粒子群优化算法的研究与改进[D].大连:大连海事大学，2008:11-15.

[15] 王维博.粒子群优化算法研究及其应用[D].成都：西南交通大学，2012：16-19.

[责任编辑：张德福]

Application of combined model based on particle swarm optimization in deformation analysis

WANG Xianpeng1,2，HUANG Shengxiang2，LI Guanqing2

(1.Guangzhou Zengcheng Land Resources and Urban Planning Bureau,Guangzhou 511300,China;2.School of Geodesy & Geomatics,Wuhan University,Wuhan 430079,China)

In a parallel combined model being built to predict deformation,one of a key issue is to determine the weights of individual model.This paper takes the deformation data of foundation pit as an example,by using GM (1,1) model and ARMA model to integrate a combination model and adopting the particle swarm optimization to search the optimal weights of two single models under the principle of minimum fitting error sum of squares.The results show that the method can integrate the advantages of each individual model to improve prediction accuracy,without solving linear programming problems,and can be practical.

PSO; GM(1,1) model; ARMA model; combined model; deformation analysis

引用著录：王显鹏，黄声享，李冠青.基于粒子群算法的组合模型在变形分析中的应用[J].测绘工程，2017，26(1)：73-76.

10.19349/j.cnki.issn1006-7949.2017.01.016

2015-12-24

国家自然科学基金资助项目(41274020)

王显鹏(1991-)，男，硕士.

TU196

A

1006-7949(2017)01-0073-04