预应力连续箱梁桥开裂状态弯矩重分布试验研究

2017-12-19李克忠

城市道桥与防洪 2017年11期

关键词：调幅墩顶内力

李克忠

（湖南大学设计研究院有限公司，湖南长沙410082）

预应力连续箱梁桥开裂状态弯矩重分布试验研究

李克忠

（湖南大学设计研究院有限公司，湖南长沙410082）

对连续梁的内力重分布的研究，可以帮助更好地分析连续梁的受力性能，而目前国内外对此主要是针对钢筋混凝土结构，对预应力结构尚少有研究。该试验以一个1：4的三跨预应力连续梁模型为基础，以弯矩调幅系数、边支座反力与中支座反力的比值（边/中）为基本参数，通过体外预应力加固前后的对比试验，对连续梁桥弯矩重分布规律进行了研究。试验结果表明：加固后结构的内力重分布较加固前稍大；加载至部分钢筋屈服时，加固前后各跨中最大弯矩调幅系数在-8.34%～-12.62%之间；两墩顶负弯矩区段的最大调幅系数在19.44%～29.59%之间，边/中由初始的32.1%降至28.38%～27.59%。

预应力混凝土连续箱梁；调幅系数；内力重分布；体外预应力加固；模型试验

0 引言

箱形截面具有良好的结构性能，在现代桥梁建设中得到广泛应用。近几年来对现役箱梁进行的调查发现，不少预应力箱梁包括一些全预应力构件存在严重的横向裂缝，这直接危及桥梁结构的安全性。在开裂状态下，预应力箱梁的受力状态如何，各部位之间由于刚度的变化内力如何重分布，目前国内外尚少有研究。对连续梁的内力重分布的研究，可以帮助更好地分析连续梁的受力性能、连续梁裂缝和变形规律，对桥梁的养护工作提出有益的建议。同时在连续梁的设计中，根据内力重分布的规律，可用于指导钢筋疏密调整，以充分发挥材料的强度，指导设计[1-5]。

1 模型试验概况

1.1 模型概况[6]

按1:4的比例制作了单箱单室3跨连续箱梁试验模型，模型截面尺寸及配筋见图1、图2。模型总长3×8.16 m＋2×0.2=24.88 m，顶板宽3 m，底板宽1.35 m，两端及中间支座位置设置横隔板，模型平面见图3。横断面为等截面单箱单室混凝土箱梁，混凝土强度等级为C40。箱梁模型非预应力筋采用H RB235级钢筋。共配置48根φs15.24的预应力筋束，其中26根体内预应力筋，20根体外预应力筋，临时索（JL）2根。采用后张法对预应力筋进行张拉，张拉控制吨位为195 kN/根。

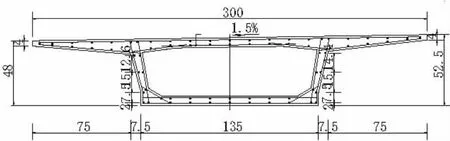
图1 模型截面尺寸及配筋（单位：cm）

图2 模型预应力筋布置图（单位：cm）

图3 箱梁模型平面（单位：cm）

试验采用500 kN级球冠型桥梁专用橡胶支座，其中中跨3-1＃支座为固定支座，其余均为滑移支座。在各支座位置布置千分表分别测量其水平位移和竖向压缩量。在支座上安装弦式力传感器测试支座反力变化，实时测量每级荷载作用下支座反力的变化和其压缩量，见图4。

图4 模型支座布置图

1.2 加载方式及工况

二期恒载和补重以均布荷载的形式施加，汽车荷载以等效集中荷载模拟。集中荷载采用油压千斤顶施加，每个千斤顶连接一个电子称，精确测试加载的荷载，加载点为各跨跨中。为了探讨预应力连续梁加固前后内力的重分布情况，试验主要分为两个步骤：（1）加固前试验研究；（2）体外预应力加固后试验研究。

试验模型见图5。

图5 试验模型概况

2 计算方法

2.1 弯矩调幅系数的计算

国内外学者曾先后提出过多种钢筋混凝土超静定结构考虑塑性内力重分布的计算方法，如极限平衡法、塑性铰法、变刚度法、强迫转动法、弯矩调幅法以及非线性全过程分析法。但由于弯矩调幅法概念明确、计算方便而被各国规范所采用。弯矩调幅法就是以弹性方法得到的弯矩值按弯矩重分布能力大小进行适当的调整，用以考虑结构因非弹性变形引起的内力重分布[1～5、7]。本文借鉴钢筋混凝土重分配的弯矩调幅法对预应力结构进行重分配分析。弯矩重分布的大小，通常用某一截面实际弯矩与弹性分析值的差值来表示，对弯矩重分布的能力和幅度，则用这一差值与弹性分析值比较，即:

2.2 理论弯矩计算和实测弯矩的得出

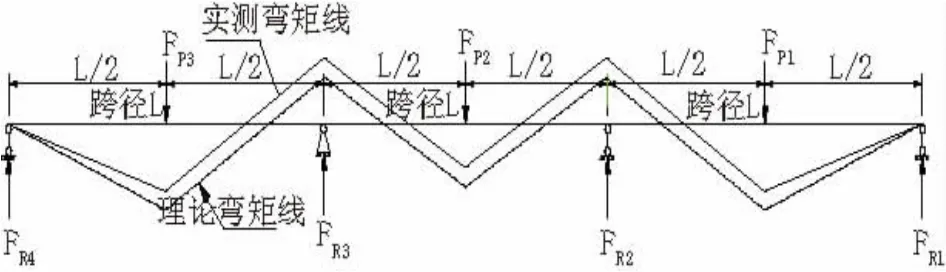
图6 理论弯矩和实测弯矩的计算图式

在试验过程中，准确得出各截面的实际弯矩是进行弯矩调幅系数计算的前提。本文采用支座反力反算各截面的弯矩，即根据实测支座反力（Fr1、Fr2、Fr3和Fr4））和实际荷载加载力（Fp1、Fp2、Fp3），采用简单的力平衡方程即可求出各截面的实测弯矩。该计算方法简单、快捷，可操作性强，同时又能考虑试验过程中由于各支座不均匀压缩（沉降）对弯矩的影响，因为其效应最终均在反力中得以体现。弯矩计算公式如求第一跨跨中的弯矩M1=FR1×（L/2）；2＃墩顶的负弯矩M2=FR1×L-Fp1×L/2。

3 试验结果及分析

3.1 加固前试验结果及分析

两边跨支座反力之和同两中支座反力之和的比值，是衡量内力重分配的一重要手段。三跨同时加载时模型各支座的反力见表1。试验过程中，模型的开裂荷载为300 kN，裂缝主要出现在跨中和墩顶负弯矩区等位置。

由图7、图8和表1、表2可知：

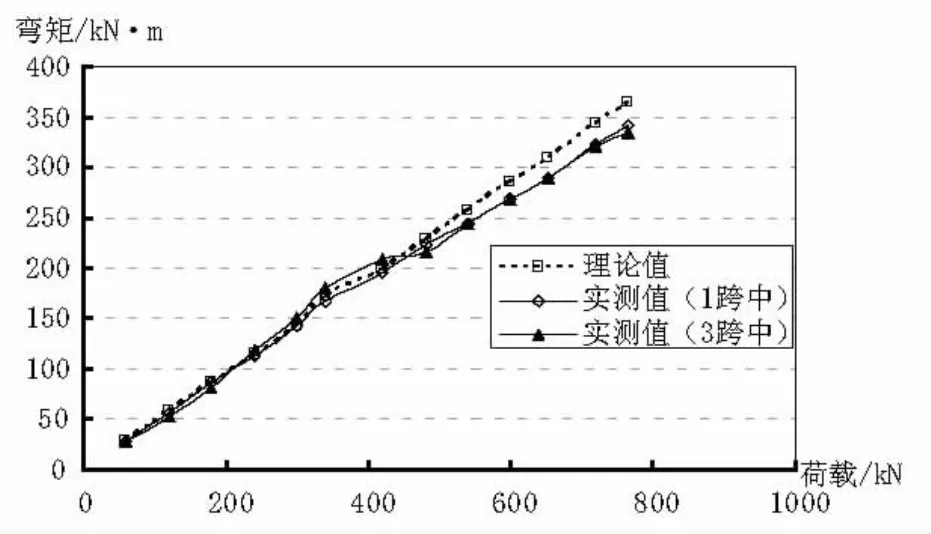
图7 加固前1、3跨跨中截面弯矩理论值与实测值

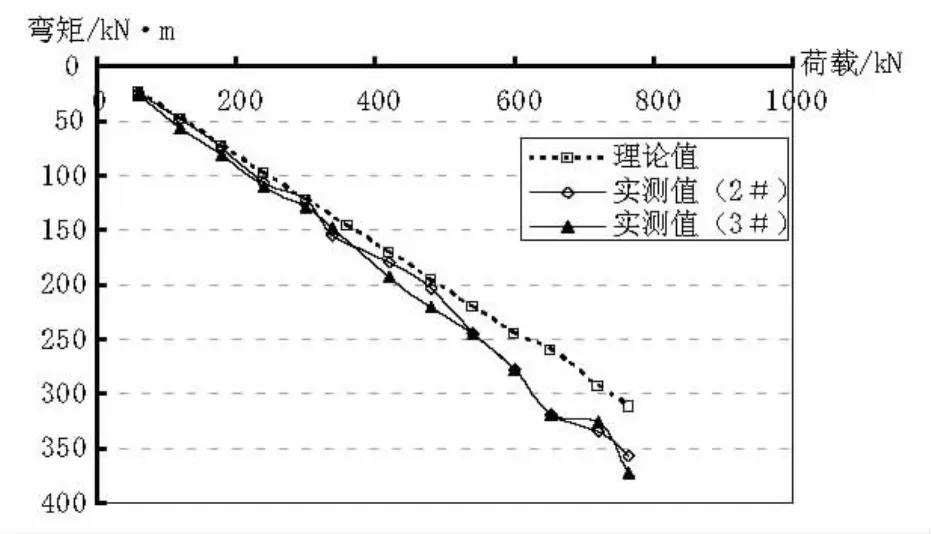
图8 加固前2＃、3＃墩顶截面弯矩理论值与实测值

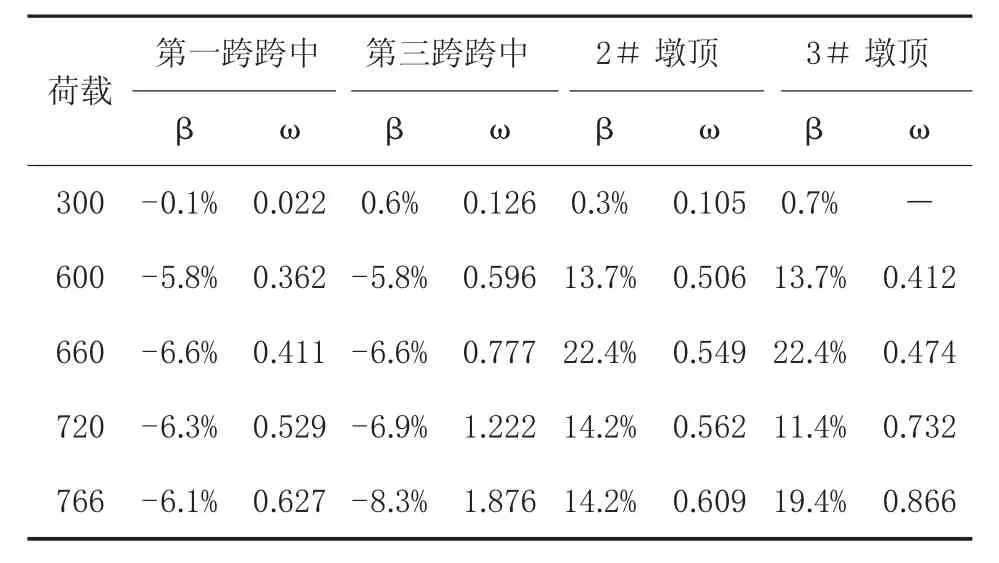
表2 加固前各截面的弯矩重分布幅度β及裂缝宽度ω

（1）边/中的初始比值为32%左右，且在480 kN之前此值变化量较小，当加载至766 kN时时此值降为28.38%。由此可得出：模型未开裂及开裂初期，各截面基本没有内力重分配；随着裂缝的发展，内力逐渐向两中支座处转移。

（2）截面开裂荷载附近（300 kN），理论值和实测值吻合良好，两者的差值不超过1%，基本未发生重分布现象，也说明测试数据的可靠性。

（3）一、三跨跨中的弯矩重分布系数均为负值，即跨中截面弯矩的增量小于其理论增量，一、三跨跨中的最大重分布幅度为-6.1%和-8.34%，第三跨跨中由于模型制作时有初始裂缝，故其重分布量相对较大。

（4）两墩顶负弯矩区的弯矩重分布幅度先逐渐增大，后又有所降低。660 kN时2＃、3＃墩顶的重分布幅度均增至22.4%；至766 kN（部分钢筋屈服）时分别降为14.2%和19.44%。由裂缝宽度增长可知，其主要与裂缝在跨中和负弯矩区段的开展速率有关。

3.2 体外预应力加固后试验结果及分析

在完成第一阶段试验工况后，模型各关键截面均已开裂且部分受力钢筋已屈服或拉断。采用体外预应力筋对其进行了加固，共张拉了20根15.24的预应力筋束。加固后模型各裂缝基本闭合，模型的开裂弯矩由加固前的300 kN提高到720 kN。

由表3、表4和图9、图10以及与未加固前结果对比可知：

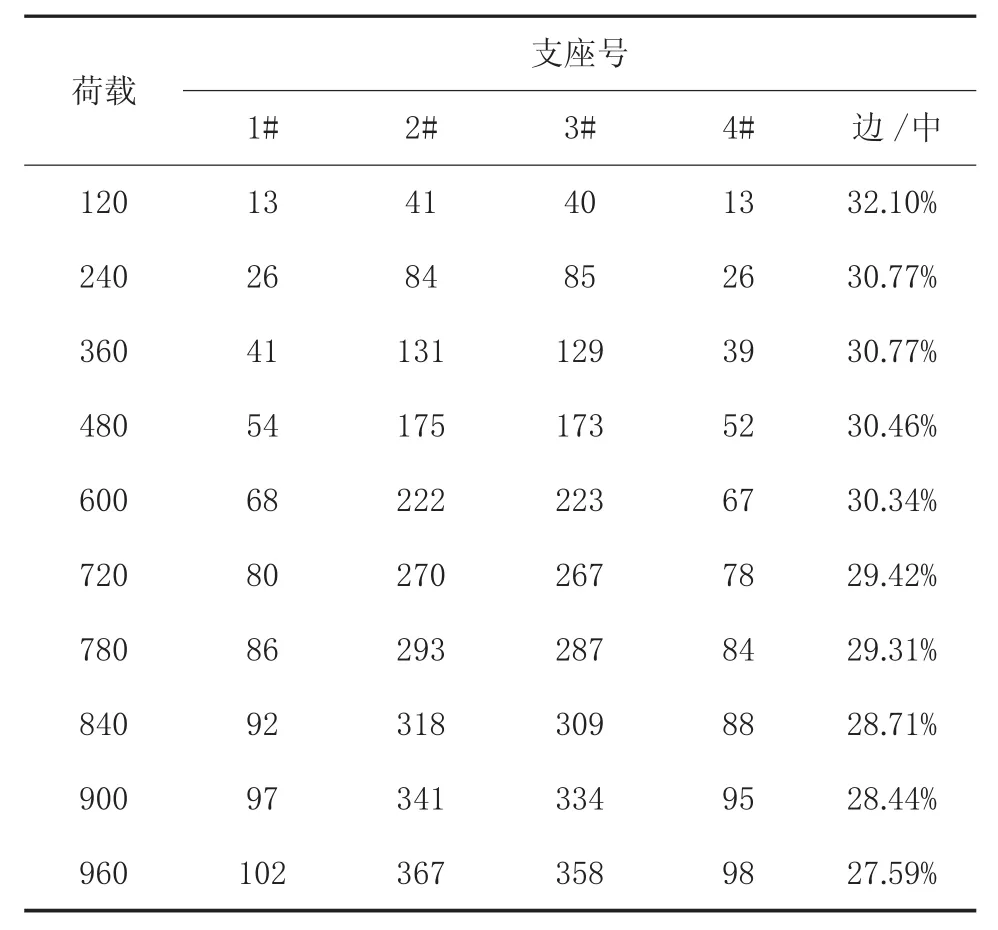
表3 加固后支座反力增量实测值kN

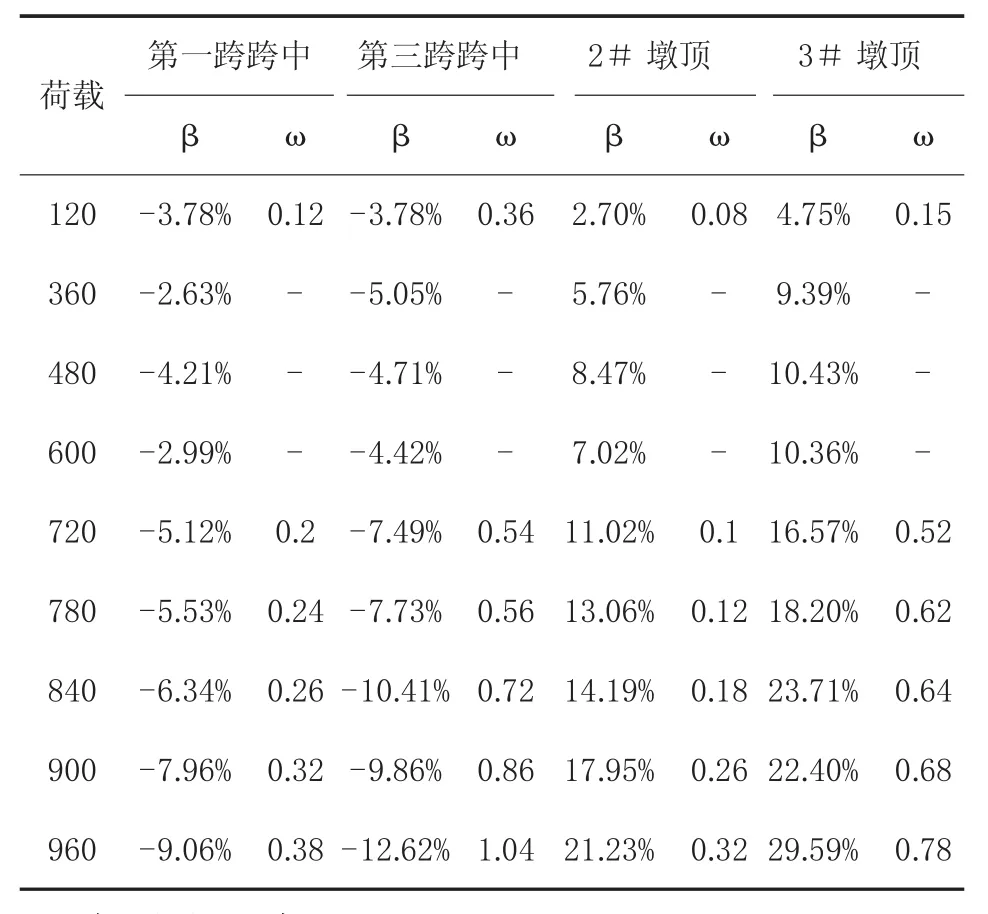
表4 加固后弯矩重分布的幅度β及裂缝宽度ω

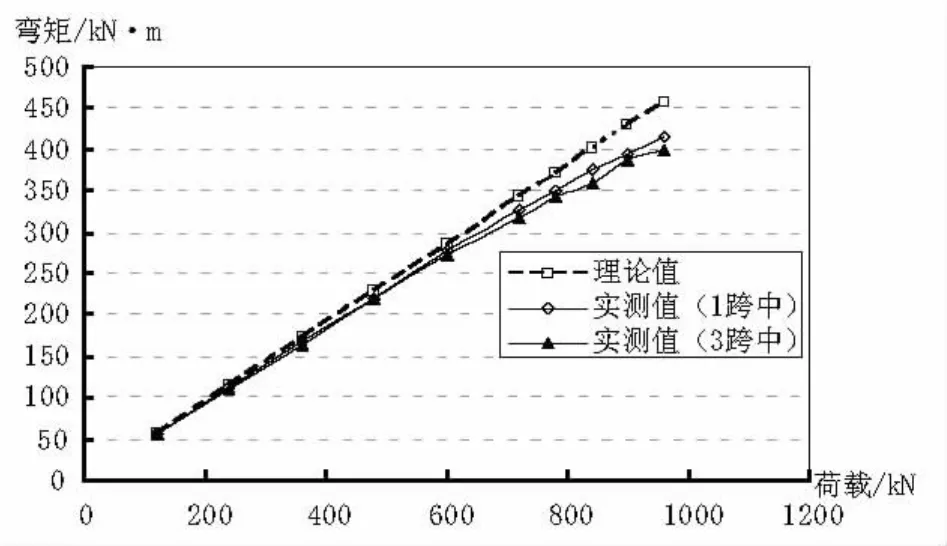
图9 加固后1、3跨跨中截面弯矩理论值与实测值

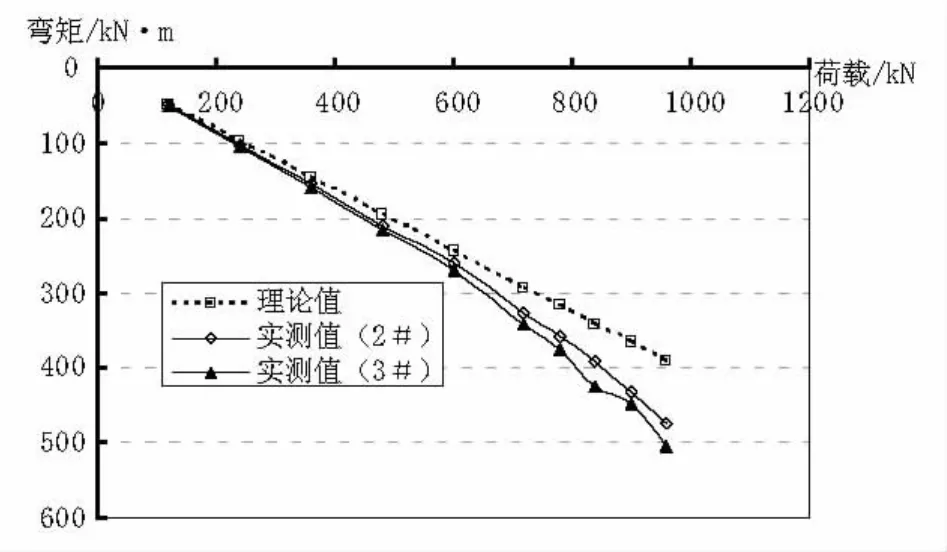
图10 加固后2＃、3＃墩顶弯矩理论值与实测值

（1）加固后边/中的初始比值为32.10%，与未加固前的初始值32.14%基本一致，说明加固后模型基本恢复到未开裂前状态。加载至部分钢筋屈服（960 kN）时，边/中之值逐渐降至27.59%，较加固前的28.38%幅度有所增加。

（2）加固前后各关键截面弯矩重分布的趋势与加固前基本一致，但在相同的荷载作用下，加固后各截面的重分布幅度较加固前小，主要原因为体外预应力加固提高了结构的开裂荷载，相同荷载下加固后裂缝开展程度不如加固前强烈。

（3）加载至部分钢筋屈服（960 kN）时，加固后一、三跨跨中的弯矩重分布幅度分别为-9.06%和-12.62%，2＃、3＃墩顶负弯矩区段的重分布幅度分别为21.23%和29.59%，相同状态下加固后的重分布系数较加固前有所提高，结构的延性增大。主要因为体外筋增大了结构受力钢筋的面积，同时体外筋的应力尚不高，故其延性才有所提高。