随机度反馈策略对路网中交通流的影响
2017-12-19马新露
彭 勇,贺 琳,罗 佳,刘 星,马新露
(重庆交通大学交通运输学院,山地城市交通系统与安全重点实验室,重庆 400074)
随机度反馈策略对路网中交通流的影响
彭 勇,贺 琳,罗 佳,刘 星,马新露
(重庆交通大学交通运输学院,山地城市交通系统与安全重点实验室,重庆 400074)
考虑到现实路况的复杂性,建立备选路径路宽不同、车道数存在差异的路网模型,并提出了新的反馈策略——随机度反馈策略.通过分析随机度、平均速度、车辆数以及交通流量反馈策略对该路网模型交通流特性参数的影响,探究随机度反馈策略的优越性.仿真结果表明:随机度反馈策略下,路网中车辆运行有序,接近出口处道路上车辆排队长度短,车辆速度大.同时,通过分析平均流量随动态车比例变化情况可知,当动态车比例不大于0.6时,平均速度、车辆数及随机度反馈策略有效性相当;当动态车比例大于0.6时,平均速度、车辆数反馈策略下平均流量降低明显,策略失效,而随机度反馈策略下平均流量变化平稳,该策略能有效改善路网道路车辆通行状况.
信息反馈策略;双通道系统;平均速度;车辆数;交通流量;随机度
0 引言
近年来,交通拥堵问题严重制约着城市的发展.城市交通并不是所有的道路同时处于拥挤状况,当部分道路处于拥挤状态、另外一部分道路却交通畅通时,若能使车辆均衡地分配在道路网络上,交通拥挤现象将会得到改善.交通诱导便是通过现有通讯方式向驾驶员反馈实时道路信息,对驾驶员出行路线加以引导,从而均衡分配路网交通流,缓解交通拥挤状态.而信息反馈策略是否合理成为交通诱导能否发挥其有效性的前提和关键.
一些专家学者就不同路网模型中合理的信息反馈策略进行了研究.在路网模型构建方面,已有的路网模型主要为双通道模型,包括双出口双通道模型、单出口双通道模型以及含瓶颈的双通道模型等.[1-4]而信息反馈策略以早期提出的3种经典策略(行驶时间反馈策略[5]、平均速度反馈策略[6]及拥挤系数反馈策略[7])为主,并在此基础上加以改进完善,提出了车辆数反馈策略、加权平均速度反馈策略、加权拥挤系数反馈策略等.[8-13]通过对已有研究分析总结发现,路网模型中可选路径道路宽度相同,不同的路网模型对应的合理信息反馈策略存在差异,且信息反馈策略的有效性存在提升空间.信息反馈策略采用的是常见的平均速度、车辆数等指标反映道路上车辆运行状况,通过查阅相关文献,了解到随机度指标同样具有反映车流不同运动状态的功能.[14]本文考虑现实路况的复杂性,构建可选路径道路宽度不一致的路网模型,并在此基础上引入随机度概念,制定随机度反馈策略,进而研究不同信息反馈策略下路网交通流特性,探讨合理的信息反馈策略.
1 含双车道的双通道道路模型
通过对已有信息反馈机制相关研究发现,大都是基于一些简单的均为单车道的双通道道路模型.在日常生活中,道路状况要复杂许多,存在可选路径的道路宽度不一致的情况.故本文考虑此种情况,建立含双车道的双通道模型.
1.1 模拟路网及道路车辆介绍
本文所研究的路网如图1所示,该双通道系统单入口、单出口,可供选择的两条道路一条为单车道,一条为双车道,且道路1和2的长度相等.为便于观察道路车辆运行情况,本文将整个路网离散网格化,其中道路1占据L1个元胞,道路2占据L2个元胞.

图1 含双车道的双通道道路模型
本文模型共有2种类型的车辆:一种为动态车,即车辆驾驶员根据实时信息提示做出路径选择;另一种为静态车,即车辆驾驶员将忽略实时信息而按照自己的意愿或偏好随机选择道路行驶.
1.2 道路车辆运动规则
元胞自动机模型具有时间、空间的离散性,同时还具有动力学演化的同步性,能够很好地模拟道路内车辆通行状况,精确地反映交通流的特性.[15]本文采用元胞自动机(CA)模型来仿真模拟车辆在上述含双车道的双通道路网中的运动.其中单车道的道路1采用经典的NS模型,双车道的道路2采用改进的双车道多值CA模型.
1.2.1 NS模型
NS模型是在1992年由Nagel和Schreckenberg[15]提出的,其基本思想是:将时间、空间以及速度离散化,即将道路等分为离散的格子即元胞,每辆车可占据1个元胞,车辆的速度可以取0~vmax1之间的任一整数值,其中vmax1为道路上车辆允许的最大行驶速度.每一时步,系统参照下列行驶规则对每辆车的速度及位置进行更新.更新规则如下:
step1:加速,ifvi step2:减速,ifdi≤vi,vi=min(vi,di); step3:随机慢化,if rand(1) step4:位置更新,xi=xi+vi. 其中:vi表示第i辆车的速度;di表示第i辆车与前方邻近车辆的间距;pslow1表示道路1上车辆的随机慢化概率;xi表示第i辆车的位置. 1.2.2 改进的双车道多值CA模型 多值元胞自动机模型是对CA184的扩展,规定元胞的容量是M,即每个元胞最多可以包含M辆车.[16]应用此模型时,没有考虑M个车道内车辆间的具体换道行为.该模型中元胞内车辆的个数可以是0~M之间的任一整数.本文采用改进的多值元胞自动机模型,对道路2上的车流进行建模.将道路2划分为离散的格子即元胞,每个格子中最多有2辆车,车辆的速度可以取0~vmax2之间的任一整数值,其中vmax2为道路上允许车辆行驶的最大速度.当元胞取值为2时,速度大的车辆先行,即如果前方的元胞上有空位,速度大的车辆先根据以下更新规则驶入前方元胞,速度小的车辆在速度大的车辆速度及位置更新后,再选择满足以下更新规则的元胞驶入. 每一时步,系统按下列规则对每辆车的速度及位置进行更新,更新规则如下: step1:加速,ifv1j Step2:随机慢化,if rand(1) Step3:不同车辆数元胞中车辆减速及位置更新. (1) 当第j个元胞中车辆数为1时. (a) 减速,ifdj≤v1j,v1j=min(v1j,dj); (b) 位置更新,x1j=x1j+v1j. (2) 当第j个元胞中车辆数为2时(假设v1j≥v2j). (a) 速度大的车辆减速,v1j=min(v1j,dj); (b) 速度大的车辆位置更新,x1j=x1j+v1j; (c) 再次搜索前方有2辆车的元胞位置,得出dj,v2j=min(v2j,dj); (d) 第j个元胞中另一辆车位置更新,x2j=x2j+v2j. 其中:v1j,v2j分别表示第j个元胞上车辆的速度,若第j个元胞上只有1辆车,则v2j=0;dj表示第j个元胞与前方有2辆车的元胞的距离;pslow2表示道路2上车辆的随机慢化概率;x1j和x2j分别表示原第j个元胞上的车辆更新后的位置. 本文道路模型的入口设置为双车道,每一时步,各车道上队列最前面的一辆车将试图进入道路1或道路2,若该辆车为动态车,则将根据出口反馈回来的最新信息选择道路进入;若该辆车是静态车,则将以一定概率选择进入道路1或道路2,由于道路2路面较宽,驾驶员凭经验进入道路2的概率较大.当队列最前方车辆进入道路1或道路2后,后方车辆依次向前移动1个元胞,最后在队列的最后各车道上以概率p产生一辆新车. 出口也将设置为双车道,即每一时步,最多只有两辆车可以离开该路网.道路1和道路2上的车辆以速度大的先出为原则离开系统,则车辆在出口处的竞争出车具体规则如下: (1) 当只有道路1或道路2上有车欲离开系统时,道路1或道路2上欲离开的车辆均可离开系统; (2) 当道路1上和道路2上均有1辆车欲离开系统时,道路1和道路2上的车辆均可离开系统; (3) 当道路1上有车辆欲离开系统而道路2上有2辆车欲离开系统时,若道路2上欲离开的2辆车的速度均不小于道路1上欲离开的车辆的速度,则道路2上欲离开的2辆车均可离开系统;若道路2上欲离开车辆中有1辆车的速度小于道路1上欲离开车辆的速度,则道路1上欲离开车辆以及道路2上欲离开的两辆车中速度大的车辆可离开系统,而欲离开却不能离开的车辆需在出口处等待下一秒放行. 典型的信息反馈策略包括行程时间反馈策略、平均速度反馈策略以及拥挤系数反馈策略.研究发现:一方面行程时间反馈策略具有一定的滞后性,不能真实反映道路实时状况;另一方面,本文所提出的双通道模型含有双车道路径,使用拥挤系数反馈策略在区分拥挤簇时,存在难以界定的问题,故本文在这3种典型的信息反馈策略中选择了平均速度反馈策略进行研究.分析不同信息反馈策略对道路交通流的影响,本文将常用的车辆数及交通流量信息反馈策略纳入进来,并制定了新的信息反馈策略——随机度反馈策略. 平均速度反馈策略:该策略由Lee等[6]提出.每一时步,道路上的车辆将其行驶速度信息发送给交通控制中心,交通控制中心根据公式 (1) 分别计算道路1、道路2上车辆的平均速度,然后将计算结果反馈给入口处的车辆.在入口处,动态车将选择平均速度大的道路驶入. 车辆数反馈策略:每一时步,交通控制中心统计每条道路上的车辆数,由于道路2为双车道道路,故将统计的道路2上车辆数总和的一半以及道路1上车辆数总和反馈给入口处的车辆,入口处动态车选择车辆数少的道路驶入. 交通流量反馈策略:每一时步,交通控制中心搜集道路上车辆平均速度及密度信息,计算出道路交通流量,然后将流量信息反馈给入口处的车辆.在入口处,动态车选择交通流量小的道路驶入.交通流量为 (2) 其中:ρ为车辆密度,N为道路上的车辆数,L为道路长度. 随机度反馈策略:每一时步,交通控制中心搜集道路上车辆的位置信息,计算出每辆车与前车车头间隙,计算出道路车辆随机度,并反馈给入口处的车辆.在入口处,动态车选择随机度大的道路驶入.其中随机度R是指在车流的各种组合运动中单个车辆的行驶自由度,其计算公式为 (3) 其中:R为车流总体随机度,N为道路上的车辆数,f(hi)为第i辆车与前车之间的影响系数.f(hi)计算公式为 其中:hi为第i辆车与前车间隔,h0为车辆间相互独立的车辆间隔,hmin为跟驰状态的车辆间隔. 本文采用MATLAB进行模拟仿真,仿真过程中,设入口道路长度L0=200个元胞,道路1、道路2的长度相同,L1=L2=3 000个元胞,每个元胞的长度为7.5 m,故道路1、道路2的实际长度为22.5 km.道路1和道路2上车辆的最大速度vmax1=vmax2=3个元胞/时步,车辆随机慢化概率pslow1=pslow2=0.3.初始时,道路1上车辆数q1=1 200辆,道路2上车辆数q2=2 000辆.入口道路及出口道路的车道数RN0=2,道路1的车道数RN1=1,道路2的车道数RN2=2.由于道路2的条件较好,静态车驾驶员选择进入道路2的概率比选择进入道路1的概率大,故设静态车选择道路1的概率px=0.3.程序运行25 000 步左右,所有的模拟结果均是选取20 000~23 600步的数据,折合成实际时间为1 h.当入口处车辆到达概率较大时,容易产生交通拥堵,此时智能交通系统将发挥作用,故设入口道路上车辆产生概率p=0.9. 以固定动态车比例为0.5,分别模拟应用4种不同的策略时路网中不同路段车辆平均速度、车辆数的演化情况,从而分析不同的反馈策略对路网中交通流的影响(见表1). 表1 采用4种策略时道路车辆数和速度的平均值 从表1中可以看出,当道路上的车辆数高时必然会导致车速下降.含双车道的双通道道路模型采用新的信息反馈策略——随机度反馈策略时,道路上所有车辆的平均速度明显高于已有策略,道路平均车辆数低于已有策略,而整体来看道路平均流量仅低于车辆数反馈策略.为了查明以上现象产生的原因,需要对路网中道路不同路段交通流状况进行分析,故将道路1和道路2每100个元胞长度视为一个路段,共分为30个路段,并对每个路段车辆数及平均速度进行统计分析. 采用不同反馈策略时,路网中不同路段车辆平均速度的变化情况见图2.由图2可知:除采用交通流量反馈策略外,采用其他策略时,接近路网出口处道路1上车辆速度有一个急剧下降的过程.采用平均速度反馈策略及随机度反馈策略时,距离出口100个元胞路段道路1上车辆速度较小,且该路段随机度反馈策略下车辆速度大于平均速度反馈策略,其他路段道路1和道路2上的速度基本一致.故采用平均速度反馈策略及随机度反馈策略时道路1和道路2上车辆平均速度相差较小,且采用平均速度反馈策略时路网道路上车辆平均速度低于采用随机度反馈策略.采用车辆数反馈策略时,道路1上车辆在距离出口600个元胞处速度骤降,然后趋于平稳,且稳定后的车速远低于平均速度反馈策略及随机度反馈策略下道路1上车辆最低速度.故采用车辆数反馈策略时,道路1和道路2上车辆平均速度相差较大,且路网道路上车辆的平均速度远低于采用平均速度反馈策略及随机度反馈策略.采用交通流量反馈策略时,道路1上各路段车辆速度均较低,故该反馈策略下路网道路上车辆平均速度最小. 图2 采用4种策略时路网中不同路段车辆平均速度变化图 采用不同反馈策略时,路网中不同路段车辆数的变化情况见图3.由图3可知:不同反馈策略下,路网中道路2上各路段车辆数基本一致,说明道路2上车辆分布较均匀.交通流量反馈策略下,道路1上车辆分布较均匀,其他3种反馈策略下,道路1上接近出口处车辆数剧增,这说明接近出口处道路1上车辆聚集产生了排队现象.观察平均速度、车辆数及随机度反馈策略下,接近出口处车辆数的变化曲线可以看出,车辆数反馈策略下,道路1上车辆排队长度最长;随机度反馈策略下,道路1上车辆排队长度最短.故路网道路上平均车辆数随机度反馈策略下最少,交通流量反馈策略下最多. 图3 采用4种策略时路网中不同路段车辆数变化图 综上所述,当动态车比例为0.5时,平均速度、车辆数、交通流量及随机度反馈策略对道路1、道路2上交通流的影响具有差异性,随机度反馈策略对提高整个道路上车辆的平均速度作用明显,并能改善道路1上接近出口处车辆排队问题.但不同动态车比例下,各信息反馈策略的有效性需要进一步分析确定. 前面的分析是在动态车比例一定的情况下进行的,为了了解不同动态车比例,不同策略的有效性,选取平均流量指标,对不同策略下动态车比例影响进行分析.平均流量Favg是指某一段时间内,道路上交通流量的平均值,即 (4) 其中:Fij表示在第j时刻;第i条道路上的交通流量;n表示可选择的道路数;t表示测量的总时间. 图4 采用4种不同策略时路网中平均流量随动态车比例变化曲线 采用4种不同反馈策略时路网中道路平均流量随动态车比例变化情况见图4.从图4中可以看出,除采用交通流量反馈策略外,采用其他3种策略,路网中平均流量随动态车比例变化情况存在相似性.当动态车比例小于0.6时,随机度反馈策略曲线与平均速度、车辆反馈策略曲线十分接近,呈现先增后稳定的趋势(当动态车比例小于0.2时,曲线呈上升趋势,路网中平均流量随着动态车比例的增加而增加;当动态车比例处于0.2与0.6之间时,曲线较平缓,路网中平均流量随着动态车比例的增加基本保持不变),平均速度、车辆数及随机度反馈策略的曲线之所以出现平缓区域是因为入口处的车辆如果当前时步不能进入道路1或道路2,则在入口处排队等候;当动态车比例在0.6~0.7时,平均速度反馈策略及随机度反馈策略下,平均流量曲线依旧较平缓,平均流量随动态车比例变化微弱;车辆数反馈策略下,曲线开始呈现下降趋势,随着动态车比例的增加,平均流量开始减少;当动态车比例大于0.7时,平均速度反馈策略及车辆数反馈策略下,曲线均呈下降趋势,即路网中平均流量随着动态车比例的增加而减少,且车辆数反馈策略曲线的下降速度快.随机度反馈策略下,曲线呈现波动状态,波动弧度较小,且平均流量均比无信息反馈时大.交通流量反馈策略下,有动态车时,平均流量均低于无动态车,这说明不进行信息反馈,让驾驶员随机选择道路,路网中平均流量更大.说明交通流量反馈策略不但不能改善道路通行状况,反而可能导致交通拥堵.因此,当动态车比例不大于0.6时,平均速度、车辆数及随机度反馈策略对改善路网交通状况的有效性基本一致.当动态车比例大于0.6时,考虑到当动态车比例较大时,平均速度、车辆数反馈策略下路网中平均流量低于无信息反馈,而随机度反馈策略下路网中平均流量均较大,此时随机度反馈策略用于含双车道的双通道道路具有一定的优越性. 本文在总结和分析前人工作的基础上,提出了随机度反馈策略.考虑现实路况的复杂性,构建了可选路径道路宽度不一致的路网模型,并将已有的平均速度反馈策略、车辆数反馈策略、交通流量反馈策略以及新的随机度反馈策略应用于该路网模型,进行模拟仿真.仿真得到了各路段车辆数、速度变化图以及平均流量随动态车比例变化关系图.由各路段车辆数、速度变化图可知,随机度反馈策略下,道路1上接近出口处车辆排队长度最短,车辆速度较大,道路1和道路2上车辆运行状况较好.由平均流量随动态车比例变化关系图可知,当动态车比例不大于0.6时,平均速度、车辆数及随机度反馈策略在提高整个路网平均流量方面均具有一定的优越性;当动态车比例大于0.6时,考虑到当动态车比例较大时,平均速度、车辆数反馈策略下路网平均流量低于无信息反馈时,这两种策略失效,而随机度反馈策略对改善路网道路车辆通行状况起着较大作用.综上,随机度反馈策略用于含双车道的双通道路网模型最优. [1] HE Z B,CHEN B K,JIA N,et al.Route guidance strategies revisited:comparison and evaluation in an asymmetric two-route traffic network[J].International Journal of Modern Physics C,2014,25(4):1450005-01-11. [2] JIANG R,WU Q.Spatial temporal patterns at an isolated on-ramp in a new cellular automata model based on three-phase traffic theory[J].Journal of Physics A,2003,36(381):8197-8213. [3] FUKUI M,ISHIBASHI Y,NISHINARI K.Dynamics of traffic flows on crossing roads induced by real-time information[J].Physical A,2013,392: 902-909. [4] ZHU K L,BI J T,WU J J,et al.Effects of speed bottleneck on traffic flow with feedback control signal[J].Modern Physics Letters B,2016,30(25):1650323-1-12. [5] WHALE J,BAZZAN A L C,KLUGL F,et al.Decision dynamics in a traffic scenario[J].Physical A,2000,287(3):669-681. [6] LEEK,HUI P M,WANG B H,et al.Effects of announcing global information in a two-route traffic flow model[J].Journal of the Physical Society of Japan,2001,70:3507-3510. [7] WANG W X,WANG B H,ZHENG W C,et al.Advanced information feedback in intelligent traffic systems[J].Physical Review E,2005,72: 066702. [8] DONG C F,MA X,WANG B H.Weighted congestion coefficient feedback in intelligent transportation systems[J].Physics Letters A,2010,374: 1326-1331. [9] XIANG Z T,XIONG L.A weighted mean velocity feedback strategy in intelligent two-route traffic systems[J].Chin Phys B,2013,22(2):028901-1-10. [10] ZHAO X M,XIE D F,LI Q.Approaching system equilibrium with accurate or not accurate feedback information in a two-route system[J].Computer Physics Communications,2015,187:106-114. [11] CHEN B K,TONG W,ZHANG W Y,et al.Flux information feedback strategy in intelligent traffic systems[J].A Letters Journal Exploring the Frontiers of Physics,2012,97(14001):1-6. [12] SUN X Y,DING Z J,HUANG G H.Effect of density feedback on the two-route traffic scenario with bottleneck[J].International Journal of Modern Physics C,2016,27(6):1650058-1-12. [13] LI W T,LI J Q,CHEN B K,et al.Information feedback strategy for beltways in intelligent transportation systems[J].Europhysics Letters,2016,113(6):64001-64010. [14] 罗霞,杜进有,陈应文.混合车流交通流特性分析[J].西南交通大学学报,2000,35(3):297-300. [15] NAGEL K,SCHRECKENBERG M.A cellular automaton model for freeway traffic[J].Journal de Physique Ⅰ,1992,2(12):2221-2229. [16] NISHINARI K.A lagrange representation of cellular automation traffic-flow models[J].Phys A:Math Gen,2001,34:10727-10736. Influenceofrandomizingdegreefeedbackstrategyontrafficflowinroadnetwork PENG Yong,HE Lin,LUO Jia,LIU Xing,MA Xin-lu (School of Traffic & Transportation,Chongqing Jiaotong University,Chongqing 400074,China) Considering the complexity of road conditions,a road network model with different path widths and different lanes is established.A new feedback strategy of randomizing degree feedback strategy is proposed.By analyzing. The influence of the randomizing degree,average speed,number of vehicles and flux feedback strategy on the traffic flow parameters of the road network model,the superiority of randomizing degree feedback strategy was studied.The simulation results show that under randomizing degree feedback strategy,the vehicle runs orderly in the road network,the queuing length of the velicles near the exit is short,the speed is high.At the same time,when the dynamic vehicle ratio is less than 0.6,the average speed,the number of vehicles and the randomizing degree feedback strategy are equivalent;when the dynamic vehicle ratio is more than 0.6,the average speed,number of vehicles,the average flow under feedback strategy reduce significantly,and the average flow changes in a smooth with randomizing degree feedback strategy.Randomizing degree feedback strategy can effectively improve road network traffic conditions. information feedback strategy;two-route model;mean velocity;vehicle number;flux;randomness degree 1000-1832(2017)04-0059-07 10.16163/j.cnki.22-1123/n.2017.04.012 2016-01-12 国家自然科学基金资助项目(61403052). 彭勇(1973—),男,博士,教授,主要从事交通运输规划与管理、企业运营管理与优化研究. U 491.1学科代码580·20 A (责任编辑:石绍庆)1.3 出入口规则
2 信息反馈策略
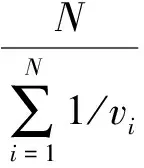
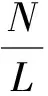

3 数值模拟
3.1 路网中各路段车辆数、速度变化情况分析



3.2 动态车比例对路网交通流的影响


4 结论
