均值方差准则下时间一致的再保险和投资策略选择

杨 鹏，刘 琦

(西京学院理学院，陕西 西安 710123)

均值方差准则下时间一致的再保险和投资策略选择

杨 鹏，刘 琦

(西京学院理学院，陕西 西安 710123)

基于两种相依保险业务，研究了最优的再保险和投资策略选择问题.研究的目标是使保险人选择时间一致的最优再保险-投资策略，最大化终止时刻财富均值的同时，最小化终止时刻财富的方差.应用动态规划理论，求得了时间一致的最优再保险和投资策略以及相应值函数的显式解.最后利用算例并结合理论分析，给出了模型参数对最优再保险和投资策略的影响.

理赔相依；均值-方差准则；时间一致；随机控制；再保险；投资

0 引言

文献[1]首次在均值-方差准则下，研究了最优策略选择.进入21世纪，越来越多的学者关注于均值-方差问题.文献[2]提出了研究均值-方差问题的线性二次控制方法；文献[3]把均值-方差问题引入到保险风险模型；文献[4]将均值-方差问题引入到资产负债管理模型；文献[5]研究了CEV模型的均值-方差策略选择问题；文献[6]把均值-方差问题推广到随机微分博弈中.

上面提到的策略均为时间不一致策略，时间一致的策略是指对于固定的时刻t和时间的增加量Δt>0，最优策略在时刻t和时刻t+Δt一致.现实中，投资者在不同时间的投资偏好可能会有所不同，但投资者在多数情况下都想寻找时间一致的策略.文献[7]在经典保险模型下，研究了时间一致的再保险和投资策略选择；文献[8]在Heston模型中，考虑了时间一致的策略选择问题；文献[9]在跳-扩散金融市场下，研究了时间一致的策略选择问题；文献[10]把时间一致策略问题推广到了CEV模型.文献[11-12]也研究了时间一致的策略问题.

运用随机控制理论研究保险风险模型的最优再保险和投资问题，是保险精算中的一个热点问题.文献[13]首先提出并探讨了此类问题；文献[14-15]在最小化破产概率下，研究了风险模型的最优再保险和投资问题；文献[16-17]在最大化期望红利的条件下，研究了风险模型的最优再保险和投资问题；文献[18-19]在最大化终止时刻财富的期望效用下，研究了风险模型的最优再保险和投资问题.尽管有非常多的文献研究这类问题，但是很少有文献研究理赔相依的再保险问题.文献[20]在理赔业务相依的保险模型中，以破产概率最小为准则，研究了最优再保险问题；文献[21]考虑了与文献[20]类似的保险模型，在终止时刻财富的最大化情形下，研究了最优再保险问题.

基于文献[20-21]，本文研究了两种理赔相依的保险业务.研究目标是求得最优时间一致策略，在最大化终止财富均值的同时，使终止财富的方差最小.应用随机控制理论，建立了值函数满足的HJB方程.通过求解财富过程对应的HJB方程，得到了时间一致的再保险和投资策略的显式解.最后利用算例并结合理论分析，给出了模型参数对最优再保险和投资策略的影响.

1 模型

给定一个完备的附流概率空间(Ω，F，P)，这里P是一个实值概率，流F∶={F(t)|t∈[0，T]}满足通常条件(关于F右连续，关于P是完备的)，T<∞.金融市场包含无风险资产(银行存款、债券等)和风险资产.无风险资产的价格过程满足常微分方程dB(t)=rB(t)dt，其中r>0表示无风险利率.风险资产的价格过程满足几何Levy过程dP(t)=P(t)[μdt+σdW(t)].其中μ>r(常数)为风险资产的预期平均收益率，σ>0(常数)为风险资产的波动率，{W(t)|t≥0}是一个布朗运动过程.

本文考虑理赔相依的保险风险模型.假设保险公司有两个相互依赖的保险业务，{Xi|i=1，2，…}为第一类业务的理赔额，它们的共同分布函数为F(x)；{Yi|i=1，2，…}为第二类业务的理赔额，它们的共同分布函数为G(y).记μ11=E(X)，μ21=E(Y)，μ12=E(X2)，μ22=E(Y2).因此，两类保险业务对应的累积理赔额满足

其中M1(t)=N1(t)+N(t)，M2(t)=N2(t)+N(t).这里N1(t)，N2(t)和N(t)分别是强度为λ1，λ2和λ的齐次泊松过程，并假设它们之间是相互独立的.两种保险业务的相依性，通过共同的泊松过程N(t)体现.为了使研究的问题有意义，假设λ1，λ2，λ和理赔额的一阶矩、二阶矩满足下面关系：

(1)

总的累积理赔额表示为

(2)

定义理赔相依的风险模型为X(t)=x0+ct-S(t).其中x0≥0为保险公司最初的财富，c>0为保险公司单位时间的保费率，S(t)表示到时刻t为止总的理赔金额满足(2)式.

设再保险水平为1-q1(t)和1-q2(t)，这里q1(t)，q2(t)称为保险公司的自留额.当0≤q1(t)≤1，0≤q2(t)≤1时表示保险公司采取了再保险；当q1(t)>1，q2(t)>1表示保险公司购买了新业务，文献[3]等考虑了类似问题.设θ是再保险公司的负载，再保险保费依据期望值原理计算，则再保险保费为

ξ(q1，q2)=(1-q1(t))a1+(1-q2(t))a2，

这里a1=(1+θ)(λ1+λ)μ11，a2=(1+θ)(λ2+λ)μ21.采取比例再保险或购买新业务后，保险公司的盈余变为

(3)

设u(t)为时刻t在风险资产上投资的金额，记π(t)=(q1(t)，q2(t)，u(t))，则再保险与投资后的财富过程满足

即

(4)

定义1一个再保险和投资策略u(t)=(a(t)，π(t))是可行的，若其满足如下条件：

(ⅰ)q1(t)，q2(t)和u(t)关于F是循序可测的，并且它们都存在左极限且是右连续的；

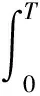
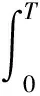
(ⅳ) 方程(4)对于策略π(t)有唯一的强解.

记所有可行的保险和投资策略集合为Π.

2 问题的提出

这里给出时间一致的均值-方差再保险-投资策略选择问题.时间一致的策略是指：对于固定的时刻t和时间的增加量Δt>0，最优策略在时刻t和时刻t+Δt一致.为此给出目标函数

(5)

这里(t，x)∈T×R，Et，x[·]=E[·|X(t，u)=x]，γ>0(常数)表示保险人的风险厌恶程度.

由定义2可知时间一致策略恰好等于平衡策略，最优值函数恰好等于平衡值函数.下文中分别称平衡策略u*和平衡值函数为最优时间一致的策略和最优值函数.

3 时间一致策略的求解

定理1(检验定理) 设F(t，x)，G(t，x)，H(t，x)为定义在[0，T]×R上的函数，其关于t连续、可微，关于x是二阶连续、可微的.如果F，G，H满足：

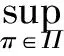
(6)

F(T，x)=x；

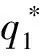
(7)

G(T，x)=x；

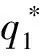
(8)

H(T，x)=x2.

(9)

则

V(t，x)=F(t，x)，G(t，x)=Et，x[X(T，u*)]，H(t，x)=Et，x[X2(T，u*)].

(10)

u*(t)=(a*(t)，π*(t))是最优时间一致的再保险和投资策略.

证明本定理的证明可参考文献[11]中定理2.1或文献[12]中定理2.1的证明过程，此处略去.

由(5)式和定理1，

从而

(11)

综合考虑盈余过程的结构和边界条件F(T，x)=x和G(T，x)=x，与文献[9，14]类似地将F(t，x)和G(t，x)形式地构造如下：

(12)

(13)

其偏导数为：

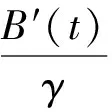
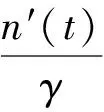
将(11)—(13)式以及上面的各偏导数代入(6)式后化简得

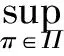
(14)

其中

A1(u)=(μ-r)u(t)A(t)-0.5σ2u2(t)m2(t)，

(15)

(16)

∂A2(q1，q2)/∂q1=-(λ1+λ)γm2(t)μ12q1(t)-λγm2(t)μ11μ21q2(t)+θ(λ1+λ)μ11A(t)，

∂A2(q1，q2)/∂q2=-(λ2+λ)γm2(t)μ22q2(t)-λγm2(t)μ11μ21q1(t)+θ(λ2+λ)μ21A(t).

令其偏导数为0，可得

(17)

证明将A2(q1，q2)关于q1，q2求二阶偏导数有

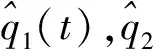
[A′(t)+rA(t)]x+B′(t)/γ+(c-a1-a2)A(t)+l3A2(t)/m2(t)=0，

(18)

其中

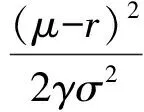
由(18)式可得

A′(t)+rA(t)=0，A(T)=1，

(19)

B′(t)/γ+(c-a1-a2)A(t)+l3A2(t)/m2(t)=0，B(T)=0.

(20)

[m′(t)+rm(t)]x+n′(t)/γ+(c-a1-a2)m(t)+l4A(t)/m(t)=0，

(21)

其中

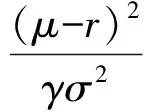
从而

m′(t)+rm(t)=0，m(T)=1，

(22)

n′(t)/γ+(c-a1-a2)m(t)+l4A(t)/m(t)=0，n(T)=0.

(23)

求解(19)和(22)式得

A(t)=m(t)=er(T-t).

(24)

将(24)式分别代入(20)和(23)式得

(25)

(26)

综上，有下面结论成立.

定理2对于财富过程(4)，最优的时间一致再保险策略为

(27)

最优的时间一致的投资策略为

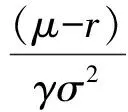
(28)

平衡值函数为

F(t，x)=xer(T-t)+B(t)/γ；

(29)

在最优策略和终止时刻T下，财富过程的方差为

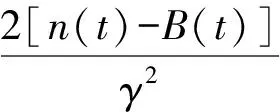
(30)

这里B(t)和n(t)分别满足(25)式和(26)式.

人才队伍建设是图书馆转型过程中的重要环节，合理的人力资源配置有利于各类型图书馆日常业务的开展。21世纪以来，随着国内外图书馆事业的发展和信息技术的广泛应用，各类型图书馆对人才的需求发生了明显的变化。当前图书馆人力资源建设存在哪方面需求，各类型图书馆的人力资源需求呈现什么特征，图书馆学教育如何满足图书馆人力资源需求，国内外图书馆界对这些问题进行了一定的探讨。

平衡值函数可通过(12)，(24)与(25)式求得.财富过程的方差可由(11)—(13)式得到.

4 敏感性分析

将(27)式关于γ求偏导得

从而最优再保险策略关于γ单调递减.这是由于γ表示投资者的风险厌恶程度，随着风险厌恶程度的增大，投资者会减少保留额，把风险转嫁给再保险者.

将(27)式关于θ求偏导得

从而最优再保险策略关于θ单调递增.这是因为θ是再保险公司的安全负载，θ增大再保险公司的保费增大，因此保险人会增加自身的保留额.

将(27)式关于r求偏导有

从而再保险策略关于r单调递减.由于r为无风险资产的利率，随着r的增大，无风险资产的预期收入将增大，从而为了减少面临的投资风险，保险人会减少保留额，把更多风险转嫁给再保险者.

将(27)式关于t求偏导有

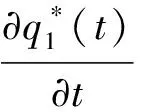
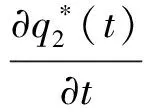
因此再保险策略关于t单调递增.这表明伴随着投资终止时刻的到来，投资者会保留更多的保险业务.

下面选取λ，λ2两个参数来讨论两种保险业务的相依性.两种保险业务的理赔分布函数为

F(x)=1-e-x，x>0；G(y)=1-e-2y，y>0.

从而μ11=1，μ12=2，μ21=0.5，μ22=0.5.

例1λ1=3，λ2=4，r=0.05，T=10，t=5，θ=1，λ∈[2，5].

例2λ1=3，λ=4，r=0.05，T=10，t=5，θ=1，λ2∈[2，9].

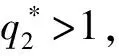
图1 λ对最优再保险策略的影响

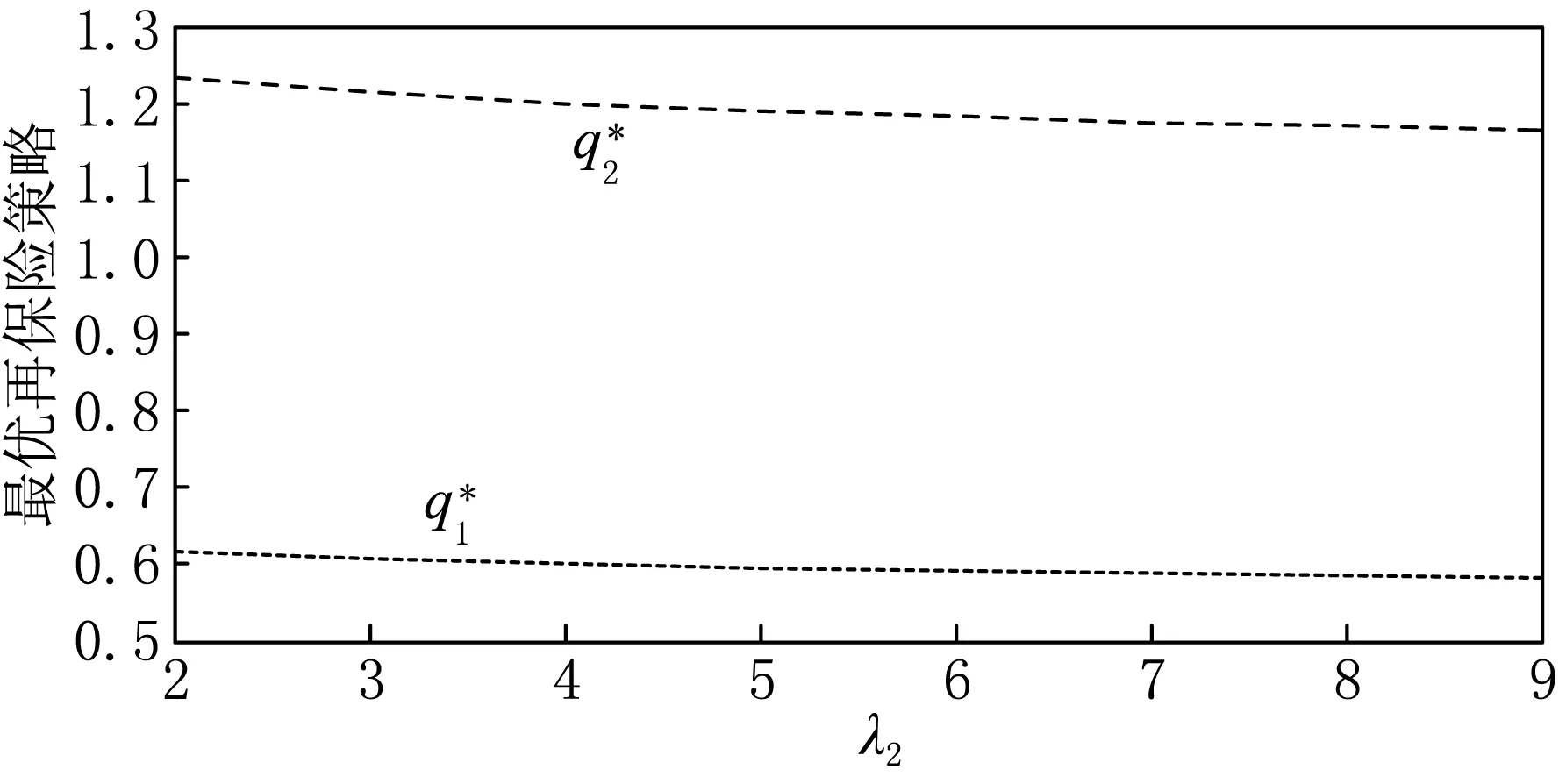
图2 λ2对最优再保险策略的影响

5 总结

在保险实务中，保险公司一般都会采取多种再保险业务.不同的再保险业务之间是相互依存的，但目前还很少有学者研究这种问题，因此本文研究了两种理赔相依的最优再保险和投资问题.研究目标是使保险人选择时间一致的最优再保险-投资策略，最大化终止时刻财富的均值，同时最小化终止时刻财富的方差.应用动态规划理论，求得了时间一致的最优再保险和投资策略以及相应值函数的显式解.最后利用算例并结合理论分析，给出了模型参数对最优再保险和投资策略的影响.

虽然本文得到了理想的结果，但是仍有很多问题值得进一步研究.比如：(1)风险资产满足CEV模型.近年来有很多文献研究基于CEV模型的最优再保险和投资策略选择问题，但是考虑再保险时，没有发现研究理赔相依性的文献.(2)本文的投资终止时刻T是确定不变的，但若T是不确定的时间，研究起来会更有意义.

[1] MARKOWITZ H M.Portfolio section [J].Journal of Finance，1952，7(1)：77-91.

[2] ZHOU X，YIN G.Markowitz’s mean-variance portfolio selection with regime switching： a continuous-time model [J].SIAM Journal on control and optimal，2003，42(4)：1466-1482.

[3] BAUERLE N.Benchmark and mean-variance problems for insurers [J].Mathematical Methods of Operations Research，2005，62(1)：159-165.

[4] XIE S X.Continuous-time portfolio selection with liability and regime switching [J].Insurance： Mathematical and Economics，2009，45(1)：148-155.

[5] 杨鹏.均值-方差准则下CEV模型的最优投资和再保险[J].系统科学与数学，2014，34(9)： 1100-1107.

[6] 杨鹏，王震，孙卫.均值-方差准则下具有负债的随机微分博弈[J].经济数学，2016，33(1)： 25-29.

[7] LI Z F，ZENG Y，LAI Y Z.Optimal time-consistent investment and reinsurance strategies for insurers under Heston’s SV model [J].Insurance： Mathematics and Economics，2012，51(1)： 191-203.

[8] ZENG Y，LI Z F.Optimal time-consistent investment and reinsurance policies for mean-variance insurers [J].Insurance： Mathematics and Economics，2011，49(1)：145-154.

[9] ZENG Y，LI Z F，LAI Y Z.Time-consistent investment and reinsurance strategies for mean variance insurers with jumps [J].Insurance： Mathematics and Economics，2013，52(3)：489-507.

[10] LI D P，RONG X M，ZAO H.Time-consistent reinsurance-investment strategy for an insurer and a reinsurer with mean-variance criterion under the CEV model [J].Journal of Computational and Applied Mathematics，2015，283(1)：142-162.

[11] BJORK T，MURGOCI A，ZHOU X Y.Mean variance portfolio optimization with state dependent risk aversion [J].Mathematical Finance，2014，24(1)：1-24.

[12] KROBORG M T，STEFFENSEN M.Inconsistent investment and consumption problems [J].Applied Mathematics and Optimization，2015，71(3)：473-515.

[13] BROWNE S.Optimal investment policies for a firm with a random risk process： exponential utility and minimizing probability of ruin [J].Mathematics of Operations Research，1995，20(4)： 937-958.

[14] HIPP C，PLUM M.Optimal investment for investors with state dependent income and for insurers [J]. Finance and Stochastic，2003，7(3)： 299-21.

[15] LIANG Z，GUO J.Optimal proportional reinsurance and ruin probability [J].Stochastic Models，2007，23(2)： 333-50.

[16] ASMUSSEN S，TAKSAR M.Controlled diffusion models for optimal dividend pay-out [J].Insurance： Mathematics and Economics，1997，20(1)：1-15.

[17] HOJGAARD B，TAKSAR M.Optimal proportional reinsurance policies for diffusion models [J].Scandinavian Actuarial Journal， 1998(2)：166-180.

[18] LIN X，YANG P.Optimal investment and reinsurance in a jump diffusion risk model [J].The ANZIAMJ Journal，2011，52(3)： 250-262.

[19] YANG H，ZHANG L.Optimal investment for insurer with jump-diffusion risk process [J].Insurance： Mathematics and Economics，2005，37(3)： 615-634.

[20] BAI L，CAI J，ZHOU M.Optimal reinsurance policies for an insurer with a bivariate reserve risk process in a dynamic setting [J].Insurance： Mathematics and Economics，2013，53(3)：664-670.

[21] LIANG Z B.YUEN K C.Optimal dynamic reinsurance with dependent risks： variance premium principle[J].Scandinavian Actuarial Journal，2016，2016(1)：1-19.

Time-consistentreinsuranceandinvestmentstrategyselectionundermean-variancecriterion

YANG Peng，LIU Qi

(Department of Science，Xijing University，Xi’an 710123，China)

An optimal reinsurance and investment strategy selection in a risk model with two dependent classes of insurance business is considered.The objective of the insurer is to choose an optimal time-consistent reinsurance-investment strategy so as to maximize the expected terminal surplus while minimizing the variance of the terminal surplus.By using the dynamic planning approach，closed-form solutions for the optimal reinsurance and investment strategies and the corresponding value functions are obtained.Numerical examples and theoretical analysis are also provided to illustrate how the optimal reinsurance and investment strategies changes when some model parameters vary.

claims dependent；mean-variance criterion；time-consistent；stochastic control；reinsurance；investment

1000-1832(2017)04-0025-07

10.16163/j.cnki.22-1123/n.2017.04.006

2016-06-03

陕西省自然科学基础研究计划项目(2016JM1024，2016JM1032)；陕西省教育厅科研计划项目(15JK2183).

杨鹏(1983—)，男，讲师，主要从事数理金融、保险精算与风险理论研究.

O 211·6学科代码110·74

A

(责任编辑：李亚军)