sl2⊗C[t]的一类模

谭海军

(1.长春理工大学应用数学系，吉林 长春 130022； 2.东北师范大学数学与统计学院，吉林 长春 130024)

sl2⊗C[t]的一类模

谭海军1，2

(1.长春理工大学应用数学系，吉林 长春 130022； 2.东北师范大学数学与统计学院，吉林 长春 130024)

研究了流代数sl2⊗C[t]的表示理论，对流代数sl2⊗C[t]在一元多项式代数C[x]上的一类模进行了分类，并确定了所得到的模的结构.

流代数sl2⊗C[t]；多项式代数；不可约模

1 预备知识

分别用C，Z，Z≥0，N表示复数集，整数集，非负整数集和正整数集.本文中所有的向量空间是C上的向量空间.

令C[t]是以t为未定元的C上的一元多项式代数，则sl2的流代数定义为sl2⊗C[t]，其李括号定义为 [y1⊗tn，y2⊗tm]=[y1，y2]⊗tn+m，∀y1，y2∈sl2，∀m，n∈Z≥0.为研究问题的方便，∀y∈sl2，∀n∈Z≥0，将y⊗tn记作y(n)，并将y⊗1与y等同起来.这样，sl2可以看作是sl2⊗C[t]的一个子代数.对于更多有关李代数的理论，可见文献[3-4].

本文研究流代数sl2⊗C[t]的一类表示，即sl2⊗C[t]在以x为未定元的一元多项式代数C[x]上的模结构，其中，sl2的元素h的作用是x的左乘.

2 sl2⊗C[t]在C[x]上的模结构

这里主要对sl2⊗C[t]在C[x]上的模结构进行深入研究，其中，h的作用是x左乘，并对这类模进行分类，确定这类模的结构.

将sl2看作是sl2⊗C[t]的子代数，则每一个sl2⊗C[t]模的结构限制到sl2上，就是一个sl2模.那么，若C[x]作为sl2⊗C[t]模满足h的作用是x左乘这个条件，则C[x]作为sl2模也满足相同的条件.

为描述sl2在C[x]上的模结构，令σ是将x映成x-1的C[x]的代数自同构，则σ-1是将x映成x+1的C[x]的自同构.C[x]到自身的恒等映射记为Id.那么，对于sl2在C[x]的这类模的结构，引用Nilsson[5]的结果：

引理1[5]设C[x]是以x为未定元的C上的一元多项式代数.则sl2在C[x]上满足h的作用是x左乘的模结构，在不考虑非零常数倍的情况下，有如下三类互不同构的类型：

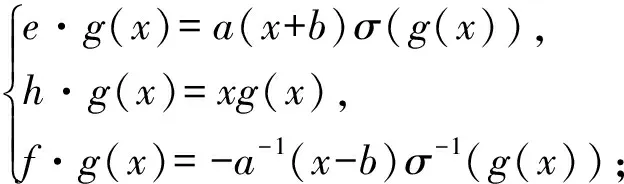
其中g(x)∈C[x]，a，b∈C是常数，且a≠0.此外，sl2模C[x]不可约，当且仅当2b∉Z≥0或(Ⅱ)与(Ⅲ)之一成立.

从sl2在C[x]上的模结构出发，可以定义sl2⊗C[t]在C[x]上的模结构.通过简单计算，有下面结论成立.

引理2任取λ∈C，∀y∈sl2，∀n∈Z≥0，令y(n)·g(x)=λn(y·g(x))，∀g(x)∈C[x]，y·g(x)是由sl2在C[x]上的模结构确定的.则C[x]成为sl2⊗C[t]模.

按照引理2定义的sl2⊗C[t]的模记作C[x]λ.当λ=0时，流代数sl2⊗C[t]在C[x]上的作用退化为sl2的作用.

定理1设C[x]是以x为未定元的C上的一元多项式代数，则流代数sl2⊗C[t]在C[x]上的模结构就是C[x]λ，λ∈C.其中h的作用是x左乘；C[x]是sl2模，其结构由引理1中(Ⅰ)—(Ⅲ)式确定.并且sl2⊗C[t]模C[x]λ是不可约的，当且仅当对应的sl2模C[x]是不可约的.

为完成定理1的证明，需要下面一些结论.

由于sl2⊗C[t]是由sl2和h(1)生成的，而sl2在C[x]上的作用是清楚的，所以只需确定h(1)的作用.

引理3存在λ∈C，使h(1)·1=λ(h·1)=λx，e(1)·1=λ(e·1)，f(1)·1=λ(f·1).

证明当sl2⊗C[t]模C[x]看作sl2模时，由引理1必有(Ⅰ)—(Ⅲ)式之一成立，从而

e·g(x)=σ(g(x))(e·1)，

f·g(x)=σ-1(g(x))(f·1)，∀g(x)∈C[x].

记h(1)·1=φ(x)∈C[x]，则由[h，h(1)]=0，有

h(1)·g(x)=g(x)(h(1)·1)=g(x)φ(x).

从而

e(1)·1=h(1)·e·1-e·h(1)·1=(e·1)(φ(x)-φ(x-1))=(e·1)(Id-σ)(φ(x))，

进一步有

e(1)·x=e(1)·h·1=h·e(1)·1-e(1)·1=(x-1)(e(1)·1)=σ(x)(e(1)·1).

对C[x]中元素的指数利用归纳法可得

e(1)·g(x)=e(1)·g(h)·1=σ(g(x))(e(1)·1)，∀g(x)∈C[x]，

从而

设φ(x)的次数为k，首项为λxk，则(Id-σ)(φ(x))的首项为λkxk-1.由引理1(Ⅰ)—(Ⅲ)式，

σ(f·1)(e·1)=-(x2-x-b(b+1))，

若λ=0，则h(1)·1=0=0x；若λ≠0且k=1，则

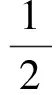
综上，h(1)·1=λ(h·1)=λx，从而

e(1)·1=h(1)·e·1-e·h(1)·1=(e·1)(Id-σ)(h(1)·1)=λ(e·1)，

f(1)·1=f·h(1)·1-h(1)·f·1=(f·1)(σ-1-Id)(h(1)·1)=λ(f·1).

定理1的证明设M=C[x]是sl2⊗C[t]的一个模，其中h的作用是x左乘.由引理3，∀y∈sl2，有y(1)·1=λ(y·1)，其中y·1是将M=C[x]看作sl2模时确定的.利用sl2的单性可知存在y1，y2∈sl2，使y=[y1，y2].则有

[y1(n)，y2(1)]=y(n+1)，∀n∈Z≥0.

利用对非负整数n的归纳法易证y(n)·1=λn(y·1).注意到∀k∈Z≥0，

y(n)·xk+1=y(n)·h·xk=h·y(n)·xk-[y(n)，h]·xk=h·y(n)·xk-[y，h](n)·xk.

对C[x]中元素的指数利用归纳法，有

y(n)·xk=λn(y·xk)，∀n，k∈Z≥0.

从而y(n)·g(x)=λn(y·g(x))，∀g(x)∈C[x]，即M=C[x]就是C[x]λ.

显然sl2⊗C[t]模C[x]λ的不可约性是由对应的sl2模C[x]的不可约性所决定的，所以C[x]λ作为sl2⊗C[t]模不可约，当且仅当对应的sl2模C[x]是不可约的.

[1] STEPHEN GELBART.An elementary introduction to the Langlands program[J].American Mathematical Society.Bulletin.New Series，1984，10(2)：177-219.

[2] SCHOTTENLOHER MARTIN.A Mathematical Introduction to Conformal Field Theory[M].Berlin，Heidelberg:Springer-Verlag，1997:47-75.

[3] HUMPHREYS JAMES E.Introduction to Lie algebras and representation theory[M].Berlin：Springer，1972:15-40.

[4] CARTER ROGER.Lie algebras of finite and affine type[M].London：Cambridge University Press，2005：121-151.

[5]NILSSON JONATHAN.Simplesln+1-module structures onU(h)[J].J Algebra， 2015，424：294-329.

Aclassofsl2⊗C[t]modules

TAN Hai-jun1，2

(1.Department of Applied Mathematics，Changchun University of Science and Technology，Changchun 130022，China； 2.School of Mathematics and Statistics，Northeast Normal University，Changchun 130024，China)

The representation theory of the current algebrasl2⊗C[t] is studied and a class ofsl2⊗C[t] modules on the algebraC[x] is classified. Thesl2⊗C[t] structures onC[t] are also determined.

current algebrasl2⊗C[t]；polynomial algebra；irreducible module

1000-1832(2017)04-0007-03

10.16163/j.cnki.22-1123/n.2017.04.002

2017-10-21

中国博士后基金资助项目(111900302，111900350)；吉林省青年科学基金资助项目(20160520111JH).

谭海军(1980—)，男，博士，主要从事李代数表示理论研究.

O 152.5学科代码110·21

A

(责任编辑：李亚军)