组合型方位体曲率分析方法
2017-12-18周元茂陈学华鑫王开华吕丙南
周元茂 陈学华 罗 鑫王开华 吕丙南 李 泂
(①成都理工大学油气藏地质及开发工程国家重点实验室,四川成都 610059; ②成都理工大学地球探测与信息技术教育部重点实验室,四川成都 610059; ③中国水利水电第七工程局有限公司试验检测研究院,四川成都 610059)
·综合研究·
组合型方位体曲率分析方法
周元茂①②③陈学华*①②罗 鑫①②王开华③吕丙南①②李 泂①②
(①成都理工大学油气藏地质及开发工程国家重点实验室,四川成都 610059; ②成都理工大学地球探测与信息技术教育部重点实验室,四川成都 610059; ③中国水利水电第七工程局有限公司试验检测研究院,四川成都 610059)
考虑到储层和地质构造的复杂多样性,为了突出储层结构及地质构造特征及其方向性,如储层的空间分布和内部的精细结构、断层和裂缝系统、褶皱等,在经典的高斯滤波方法基础上,推导了各向异性高斯迭代平滑滤波方法及其实现算法,同时建立各向异性地震体曲率分析方法,将两者联合应用,形成了地震资料的组合型方向体曲率分析方法。实际地震资料的处理结果表明,本文方法可在压制地震背景干扰的同时突出具体方向的地质异常信息。
去噪 各向异性 高斯滤波 体曲率属性
1 引言
数字滤波一直是地震勘探领域重要的研究课题之一,有效的地震资料滤波方法一直是人们的研究重点[1-4]。传统的高斯滤波器是各向同性的,滤波时对图像平滑区和边缘过渡区进行了均衡处理,这样就会导致过滤噪声后图像边缘变得模糊甚至边缘消失[5-9]。为了解决这一问题,研究者们做了大量工作,Van Ginkel等[10]提出了去卷积的方法提高高斯滤波的角分辨率,但是该方法需要用到复杂的傅里叶去卷积算法;Geusebroek等[11]提出了一种快速各向异性高斯滤波方法,通过在两个不同方向上选用不同的高斯尺度,使滤波器在去噪的同时可以较好地保留图像边缘等重要信息,并利用高斯函数的可分解性将滤波器沿长轴和短轴方向分解为两个一维滤波器与图像进行卷积,使计算简化,提高了效率。
地震属性是对地震资料的几何学、运动学、动力学及统计学特征的一种测量和描述,它反映不同的地质信息,是刻画、描述地层结构、岩性及物性等地质特征的方法[12,13],因此在油藏识别和储层预测中起着重要作用。随着20世纪80年代后期三维地震勘探的发展及普及,地震属性分析方法逐渐从二维面空间拓展到三维体空间。 Roberts[14]详述了曲率属性的基本理论,提出了第一代曲率分析方法——层面曲率属性的计算和工作流程,表明曲率属性对断层和裂缝走向等构造的几何特征的提取十分有效,为曲率属性在地震资料构造解释中的推广和应用奠定了基础; Al-Dossary等[15]利用地震数据体所包含的空间方位信息,得到了第二代曲率分析方法——体曲率属性,并在此基础之上采用分数傅里叶变换实现了体曲率属性的多尺度分析; Chen等[16]采用小波包分解实现了时间或深度方向上的多尺度分析,并通过多尺度体曲率属性的融合显示获得了更加丰富的构造细节; Chopr等[17-19]则将曲率属性与相干属性融合显示以进行构造上的识别和解释,并将地震几何属性应用于地震资料预处理中,用以监控地震数据处理的质量。
上述方法在对地震数据去噪时,由于不能对地质构造信息进行选择性识别,在地震数据去噪以及地震属性的提取时,在识别某一具体方向(如特定方向)的地质异常信息过程中会受到其他方向细微构造(如裂缝、小断层等)的干扰。本文的目的是在压制地震数据背景噪声的同时,突出特定方向的地质构造特征,提高地震资料信噪比,以便获得更精确的地质构造信息,达到高分辨率构造精细识别效果。
2 方法原理
2.1 各向异性高斯滤波器
传统高斯滤波的基本原理是将高斯核函数与原始信号进行卷积[20,21]。以二维高斯滤波为例,其滤波器表达式为
(1)
式中σ为高斯函数的基本方差,它决定了高斯核宽度,与平滑程度有直接关系,σ越大,高斯窗口越宽,平滑程度越好。在二维空间中,高斯函数是旋转对称的(图1a),对一个图像的各个方向上的平滑效果
是均衡的(即各向同性)。对于式(1),当在x、y方向选取不同的尺度时,高斯函数将不再对称,如图1b所示,其在x、y平面上的投影为椭圆(图2a)。椭圆型高斯函数为
(2)
将该椭圆沿其轴线旋转一个角度θ后,如图2b所示,可得滤波算子

(3)
其中θ为u轴与x轴之间的夹角。将式(3)中Gθ变换到频率域,可得
Gθ(ωx,ωy;σu,σv,θ)

(4)
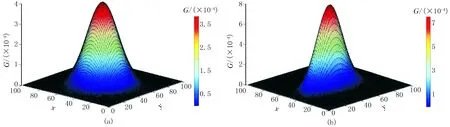
图1 二维各向同性和二维各向异性高斯滤波器
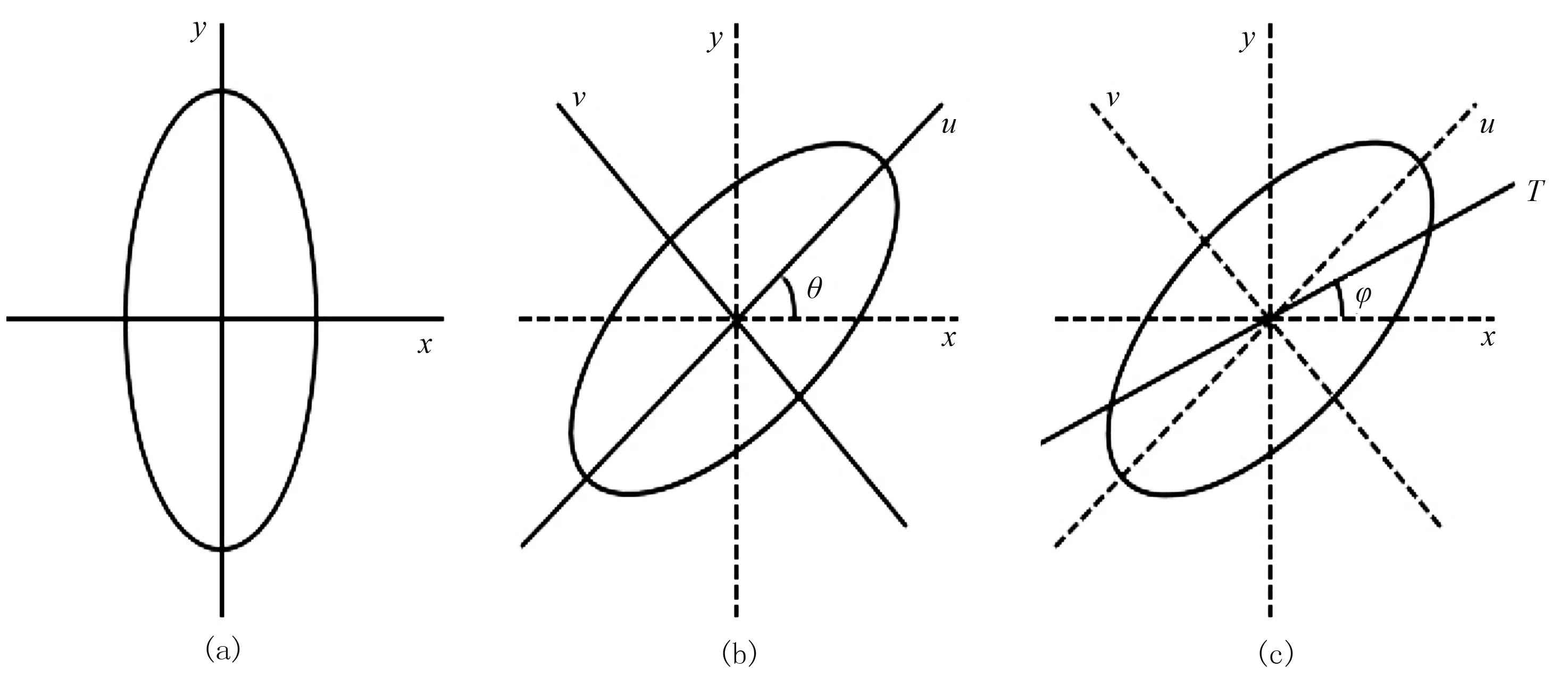
图2 各向异性高斯滤波器椭圆及其坐标系
为了使该二维滤波器能分解为沿x方向和沿y方向的一维滤波器,将上式改写为
Gθ(ωx,ωy;σu,σv,θ)
(5)
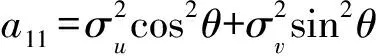
为了使滤波方向沿T(y=xtanφ)方向滤波而不是沿y方向滤波,如图2c所示,在T方向上将式(5)改写为
(6)
利用傅里叶逆变换将上式变换到时间域
(7)

(8)
其中σx为高斯函数沿x方向的标准差,即


(9)

Gθ(x,T;σu,σv,θ)=Gx(x;σx)*Gφ(T;σφ)
(10)
式中
(11)
通过将二维高斯滤波分解为两个方向上的一维滤波以实现各向异性高斯滤波,提高了运算速度,节省了计算卷积的时间。同时采用加权平滑滤波的方法可有效解决滤波过程中出现边缘模糊的问题。
2.2 三维各向异性体曲率分析
在几何地震学中,三维地震反射体在空间上的任一反射点r(z,x,y)可以认为是时间标量u(t,x,y),那么梯度grad(u)反映的是反射面沿着不同方向的变化率,即反射面沿着方向矢量所在的法截面截取的一阶导数,其结果为该反射点的视倾角向量。

(12)
式中px、py、pz分别为沿x、y和z方向的视倾角分量,如图3所示。其中:ρ为真倾角;ζ为方位角;a为沿着反射面的单位矢量倾角;ψ为走向。

图3 三维空间中倾角、方位角与视倾角的关系[22]
一个三维地震数据体可以先转化为倾角数据体,再根据倾角数据体计算其中任意点的曲率。根据复数道分析中的瞬时频率和瞬时波数计算三维地震数据体的视倾角,瞬时频率的计算需要对初始地震数据及其希尔伯特变换进行两次微分运算[23,24],而微分运算对噪声较为敏感,为了解决这一问题,Claerbout[25]提出估算瞬时频率的方法
(13)
式中:φ为瞬时相位;s(t)为初始解析信号; Δt为信号的采样间隔。
本文采用中心差分格式计算,将虚部运算化到实部,得到瞬时频率计算公式

(14)
式中:g(t)为t方向初始地震信号;h(t)为其相应的希尔伯特变换。与式(13)相比,式(14)具有更高的精度和更小的计算量,更适用于较大型的三维地震数据。
同理,可得到x方向和y方向的瞬时波数kx、ky的计算公式为
(15)
式中:g(x)、g(y)分别为x方向和y方向初始地震信号;h(x)、h(y)为其相应的希尔伯特变换。
可由瞬时频率ω和瞬时波数kx、ky计算出x方向及y方向的视倾角分量px和qy
(16)
在此基础上,构造新的方位视倾角分量
(17)
式中β为根据需要突出的地质构造所在的方向而选取的角度。通过重新计算方位视倾角分量(pβ,qβ)得到的体曲率属性可以反映某一特定方向上的构造信息。
对于三维空间中某点的曲率值,通过与其相邻道和样点的视倾角值拟合出的空间曲面方程计算得到。根据最小二乘逼近原理,得到二次曲面方程为
F(x,y)=ax2+by2+cxy+dx+ey+f
(18)
对上式方程两边求微分,并将pβ、qβ带入其中,得到了趋势面方程系数
(19)
综上可见,三维数据体中过任意点的空间曲面可由三维时窗下各个数据点的视倾角计算出来。过空间中某点的曲面可以产生任意多个曲率。最大正曲率Kpos和最小负曲率Kneg对线性构造敏感,因此在描述断层、裂缝等构造上最为有效[26,27],是用于实际地震资料构造解释的主要属性。其表达式为
(21)
3 模型试算与分析
为了验证各向异性高斯滤波的效果,设计一个切片模型(图4)。图4a为无噪声的原始模型,其中,虚线可表示地震资料中储层的断层或裂缝,图4b为加入随机噪声后的模型。使用各向异性高斯滤波算法对图4b的数据进行滤波处理,得到四个方向的滤波结果(图5)。图中θ表示选取的滤波方向(如箭头所示),其中,图5a为θ=0°时的结果,从图中可见,图4b中存在的大量随机噪声已明显减少,原本横向的虚线变成连续的实线且更为粗壮,其他方向的虚线则被明显压制。同理,图5b~图5d是方向角分别为45°、90°和135°时的滤波结果,突出的信息与滤波取向相对应。说明该方法不仅能达到去噪的效果,而且能更好地反映构造中不连续性信息,证明了方法的可行性。
图6为各向异性高斯滤波后求取的各向异性曲率(最小负曲率)属性结果。在求取各向异性体曲率属性时,选取与高斯滤波相对应的方位角。由图可见,各向异性体曲率属性效果明显,对应方向的有效信息得到了进一步加强,证明各向异性高斯滤波与各向异性体曲率相结合的方法是可行的。

图4 模型切片
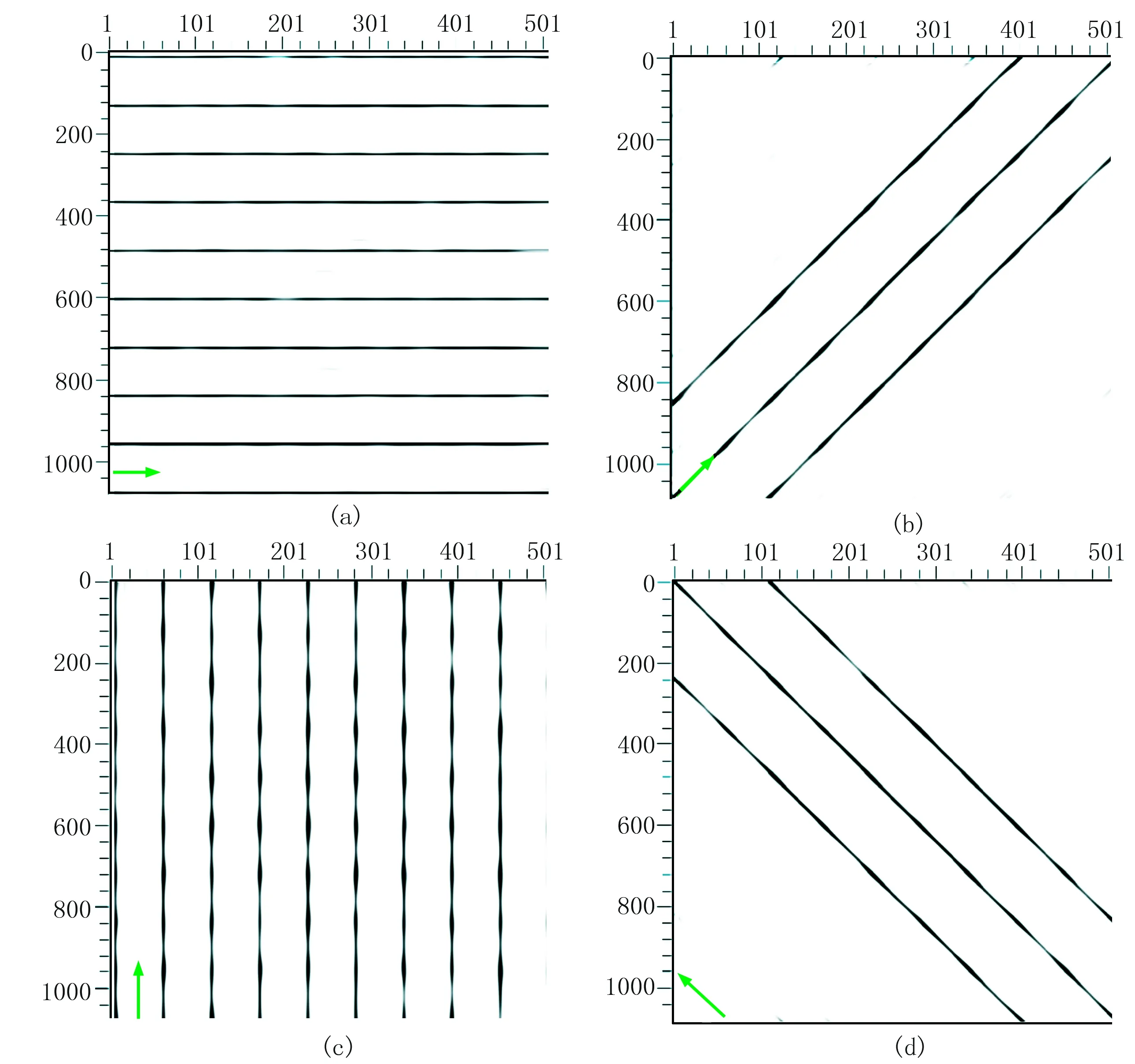
图5 经不同取向的各向异性高斯滤波处理后的结果
4 实例分析
为了验证基于地震资料的组合型方向体曲率分析方法的应用效果,对LH地区的三维叠后地震数据体进行了高斯滤波及体曲率属性提取。该地区受多期构造作用的控制,断裂系统发育。图7a为原始地震数据目的层振幅切片,该目的层位于珠江组上段,属于典型的碳酸盐岩储层,储层内部空隙发育,孔渗关系复杂,非均质性强; 图7b为滤波前求取的最小负曲率沿层切片,由图可见,随机噪声干扰严重,给后期的构造解释、断裂及展布规律的识别、储层预测等带来了困难; 图7c为地震数据体经传统高斯滤波后的最小负曲率沿层切片,可看出原先图7b中的噪声已被明显压制,图中的构造信息更加清晰。
利用本文提出的算法处理该三维叠后地震数据体,得到不同滤波方向的三维地震体曲率属性(最小负曲率)沿层切片。图8a~图8c是各向异性高斯迭代平滑滤波与各向异性体曲率相结合的处理结果,其各向异性高斯滤波的角度θ分别为0°、0°、90°,以及各向异性体曲率的方位β分别为0°、90°、90°。

图6 不同取向的各向异性体曲率属性(最小负曲率)结果

图7 LH地区的振幅和体曲率属性的沿层切片

图8 组合型方向体曲率处理后的沿层切片
对比图8a与图8c,二者差别明显,着重突出的构造特征方向不同。图8a的滤波方向角为0°,从图中可见,该切片横向不连续性且构造异常特征得到了明显的加强,其背景噪声干扰相对于图7b得到了明显压制。图8c的滤波角度为90°,该切片着重突出了纵向构造特征,其纵向断层及裂隙连续性得到明显加强,横向构造及背景噪声干扰大幅减弱。图8b为二者不同方向相结合的处理结果,在过滤大部分背景噪声的同时突出主要地质构造特征(如较大的断层、褶皱、落水洞等)。相对于传统高斯滤波及体曲率分析方法,本文提出的组合型方向体曲率分析方法有其独特的优势,在压制背景噪声干扰的同时,能够更准确地突出地震资料中特定方向上的地质异常信息,大幅减弱了背景噪声及其他方向地质信息的干扰,体现出该算法的可行性和优越性。
5 结论
本文提出了一种改进的各向异性高斯滤波方法。基于常规各向同性高斯滤波算法,推导了各向异性高斯迭代平滑滤波公式。将二维高斯滤波算法分解为两个方向上的一维滤波,通过改变滤波角度来实现定向滤波的目的,同时提高了运算速度,节省了计算卷积的时间。在三维体曲率属性的计算中加入方位参数,推导出各向异性体曲率属性分析方法,该方法可定向选取需要突出地质构造信息。将各向异性高斯滤波方法与各向异性体曲率属性分析方法联合应用,形成地震资料的组合型方向体曲率属性分析方法。该方法可对地震数据中的某一特定方向的构造信息进行两次加强,极大地突出了该方向的地质构造特征,可以更好地反映特定方向的构造细节、不连续性,为构造解释、断裂及展布规律的识别、储层预测等提供更好支持。需要指出的是,该方法在地震数据滤波及曲率属性提取时,需要根据地质构造情况,人为地选择滤波角度及提取曲率属性的方位角,还无法做到自适应滤波和自适应提取曲率属性,这点需要进一步改进。
[1] 张俊华.地震资料去噪方法——原理、算法、编程及应用.山东青岛:中国石油大学出版社,2011.
[2] 杨阳,曲寿利,印兴耀.沿层地震属性数据空间滤波去噪方法.石油地球物理勘探,2007,42(2):208-211.
Yang Yang,Qu Shouli,Yin Xingyao.Using spatial filtering for denoise of horizon-oriented seismic attri-butes data.OGP,2007,42(2):208-211.
[3] 张华,陈小宏,杨海燕.地震信号去噪的最优小波基选取方法.石油地球物理勘探,2011,46(1):70-75.
Zhang Hua,Chen Xiaohong,Yang Haiyan.Optimistic wavelet basis selection in seismic signal noise elimination.OGP,2011,46(1):70-75.
[4] 罗鑫,陈学华,齐迎凯.基于匹配滤波的保幅动校拉伸校正方法.石油地球物理勘探,2016,51(4):654-660.
Luo Xin,Chen Xuehua,Qi Yingkai.A NMO stretch correction based on an amplitude-preserved matched filtering.OGP,2016, 51(4):654-660.
[5] 姒绍辉,胡伏原,顾亚军.一种基于不规则区域的高斯滤波去噪算法.计算机科学,2014,41(11):313-316.
Si Shaohui,Hu Fuyuan,Gu Yajun.Improved denoising algorithm based on non-regular area Gaussian filtering.Computer Science,2014,41(11):313-316.
[6] 伍鹏,贺振华,陈学华.二维高斯迭代平滑滤波曲率属性及其应用.地球物理学进展,2010,25(6):2144-2149.
Wu Peng,He Zhenhua,Chen Xuehua et al.Curvature attribute of two-dimensional Gaussian iterated smoo-thing filtering and applications.Progress in Geophy-sics,2010,25(6):2144-2149.
[7] 王小兵,孙久远,汤海燕.一种高斯噪声组合滤波方法.佳木斯大学学报(自然科学版),2011,29(5):696-698.
Wang Xiaobing,Sun Jiuyuan,Tang Haiyan.A mixed filter method on Gaussian noise.Journal of Jiamusi University (Natural Science Edition),2011,29(5):696-698.
[8] 冯芳.高斯滤波运算的几种并行实现方法.兰州工业学院学报,2015,22(5):57-60.
Feng Fang.Several methods on Gaussian algorithm.Journal of Lanzhou Institute of Technology,2015,22(5):57-60.
[9] 高萌,刘吉臻,王瑞琪.基于自适应高斯滤波的电站历史数据稳态检测方法.动力工程学报,2014,34(9):708-714.
Gao Meng,Liu Jizhen,Wang Ruiqi et al.Steady-state detection of power plant history data based on adaptive Gauss filter.Journal of Chinese Society of Power Engineering,2014,34(9):708-714.
[10] Van Ginkel M,Verbeek P W,Vliet L J.Improved orientation selectivity for orientation estimation.Proceedings of the 10th Scandinavian Conference on Image Analysis,1997,533-537.
[11] Geusebroek J M,Smeulders A W M,Weijer J V D.Fast anisotropic Gauss filtering.IEEE Transactions on Image Processing,2003,12(8):938-943.
[12] 王世瑞,王树平,狄帮让.基于地震属性特征的河道砂体预测方法.石油地球物理勘探,2009,44(3):304-313.
Wang Shirui,Wang Shuping,Di Bangrang.Prediction of channel sand body based on seismic attributes.OGP,2009,44(3):304-313.
[13] 李建雄,崔全章,魏小东.地震属性在微断层解释中的应用.石油地球物理勘探,2011,46(6):925-929.
Li Jianxiong,Cui Quanzhang,Wei Xiaodong.Application of seismic attributes in micro-fault interpretation.OGP,2011,46(6):925-929.
[14] Roberts A.Curvature attributes and their application to 3D interpreted horizons.First Break,2001,19(2):85-100.
[15] Al-Dossary S and Marfurt K J.3D volumetric multispectral estimates of reflector curvature and rotation.Geophysics,2006,71(5):41-51.
[16] Chen X H,Yang W,He Z H.The algorithm of 3D multi-scale volumetric curvature and its application.Applied Geophysics,2012,9(1):65-72.
[17] Chopra S and Marfurt K J.Volumetric curvature attributes add value to 3D seismic data interpretation.The Leading Edge,2007,26(7):856-867.
[18] Chopra S,Marfurt K J.Integration of coherence and volumetric curvature images.The Leading Edge,2010,29(9):1092-1107.
[19] Chopra S,Marfurt K J.Coherence and curvature attributes on preconditioned seismic data.The Leading Edge,2011,30(4):386-393.
[20] 钱晓亮,郭雷,余博.基于目标尺度的自适应高斯滤波.计算机工程与应用,2010,46(12):14-16.
Qian Xiaoliang,Guo Lei,Yu Bo.Adaptive Gaussian filter based on object scale.Computer Engineering and Applications,2010,46(12):14-16.
[21] 章为川,程冬,朱磊.基于各向异性高斯核的多尺度角点检测.电子测量与仪器学报,2012,26(1):37-42.
Zhang Weichuan,Cheng Dong,Zhu Lei.Multi-scale corner detection based on anisotropic Gaussian kernels.Journal of Electronic Measurement and Instrument,2012,26(1):37-42.
[22] Marfurt K J.Robust estimates of 3D reflector dip and azimuth.Geophysics,2006,71(4):29-40.
[23] 李红星,饶溯,陶春辉.广义希尔伯特变换地震边缘检测方法研究.石油地球物理勘探,2015,50(3):490-494.
Li Hongxing,Rao Su,Tao Chunhui.Seismic edge detection method based on generalized Hilbert transform.OGP,2015,50(3):490-494.
[24] 李斌,陈学华,贺振华.基于多尺度加窗希尔伯特变换的地震资料体边缘检测.石油物探,2015,54(3):345-349.
Li Bin,Chen Xuehua,He Zhenhua et al.Seismic data 3D edge detection based on multi-scale windowed Hilbert transform.GPP,2015,54(3):354-359.
[25] Claerbout J F.Fundamentals of Geophysical Data Processing.McGraw-Hill Book Company,New York,USA,1976.
[26] 杨威,贺振华,陈学华.三维体曲率属性在断层识别中的应用.地球物理学进展,2011,26(1):110-115.
Yang Wei,He Zhenhua,Chen Xuehua.Application of three-dimensional volumetric curvature attributes to fault identification.Progress in Geophysics,2011,26(1):110-115.
[27] 杨威,贺振华,陈学华.结构方位滤波在体曲属性中的应用.石油物探,2011,50(1):27-32.
Yang Wei,He Zhenhua,Chen Xuehua.Application of structural azimuth filtering in volumetric curvature.GPP,2011,50(1):27-32.
*四川省成都市成华二仙区桥东三路1号成都理工大学油气藏地质及开发工程国家重点实验室,610059。Email:chen_xuehua@163.com
本文于2016年10月13日收到,最终修改稿于2017年9月10日收到。
本项研究受国家自然科学基金项目(41374134、41574130)、“十三·五”国家科技重大专项(2016ZX05014-001-009)和四川省青年科技创新研究团队项目(2016TD0023)联合资助。
1000-7210(2017)06-1253-08
周元茂,陈学华,罗鑫,王开华,吕丙南,李泂.组合型方位体曲率分析方法.石油地球物理勘探,2017,52(6):1253-1260.
P631
A
10.13810/j.cnki.issn.1000-7210.2017.06.016
(本文编辑:宜明理)

周元茂 硕士,1991年生;2014年毕业于桂林理工大学勘查技术与工程专业,获学士学位;2017年毕业于成都理工大学地球物理学院地球探测与信息技术专业,获硕士学位;主要从事地震数据的去噪以及几何属性提取方面的研究。
