基于TV约束和Toeplitz矩阵分解的波阻抗反演

2017-12-18王治强曹思远陈红灵孙晓明

石油地球物理勘探 2017年6期

关键词：子波波阻抗测井

王治强曹思远陈红灵孙晓明樊平

(①中国石油大学地球物理与信息工程学院,北京102249； ②中国石油大学油气资源与探测国家重点实验室,北京102249; ③东方地球物理公司辽河物探处,辽宁盘锦124000)

·偏移成像·

基于TV约束和Toeplitz矩阵分解的波阻抗反演

王治强*①②曹思远①②陈红灵①②孙晓明①②樊平③

利用波阻抗剖面的非高斯分布特点以及地震子波褶积矩阵的Toeplitz结构，对波阻抗剖面进行全变分(TV)约束，可以在压制随机噪声的同时保持剖面的不连续性，对地震子波褶积矩阵进行Toeplitz稀疏矩阵分解得到地震子波的稀疏表达。地震资料的低频损失导致无法反演出波阻抗的低频背景，故将测井或解释层位信息通过最小二乘法建立约束条件。建立的约束最优化目标函数可以同时反演子波和波阻抗。文中将地震剖面整体处理，反演结果比常规的逐道反演具有更高的精度、横向连续性和抗噪性。

波阻抗 TV约束 Toeplitz结构矩阵分解约束最优化

1 引言

波阻抗反演是叠后地震资料解释中非常重要的技术之一。它将地震剖面转换为波阻抗剖面，不仅便于解释人员直接对比地震资料与测井资料，而且能对地层物性参数的变化进行有效分析，得到其在空间的分布规律，指导油气勘探开发[1]。常规波阻抗反演方法是在反褶积的基础上对提取的反射系数逐道进行递推反演[2]。地震资料的低频损失导致无法反演出波阻抗的低频背景[3]，故将测井或解释层位信息通过最小二乘法建立约束条件。随着石油勘探开发的不断深入，基于同相轴追踪进行层位解释的常规方法已经无法满足目前的地质需求。借助于测井资料和地质认识，利用波阻抗反演资料综合地震资料识别地下构造、岩性已经成为地震资料解释和储层预测的重要技术[4]。然而，地震资料低频和高频信息的缺失、地震子波的未知、噪声的干扰以及地质结构的复杂性降低了地震反演的精度。根据正演模型的不同，波阻抗反演分为基于波动方程的反演和基于褶积模型的反演两大类。前者算法结构复杂、计算量大、抗干扰性差，很难获得一个稳定解，未得到广泛应用。目前主要使用基于褶积模型的反演方法，该算法相对简单，对噪声敏感性相对较小[5]。

波阻抗反演技术经历了从直接递推反演到基于模型的迭代反演的发展过程[6]。直接递推反演分两步完成，首先对地震资料进行反褶积处理，求得反射系数剖面，再对反射系数序列进行道积分得到波阻抗剖面。

基于模型的迭代反演方法以最小二乘法为基础，约束正演模型和实际监测数据之间的误差，再根据地下波阻抗的物性特征加入约束条件，建立约束最优化目标函数。通过不断修改初始模型使目标函数取得极值，即可得到最合理的解。迭代反演能够有效克服地震资料直接反演存在的带限问题[7]。

根据模型与观测数据之间的函数关系，反演问题分为线性反演和非线性反演。Cooke等[8]将波阻抗反演问题线性化，使用广义线性反演方法直接从地震剖面中逐道估计波阻抗； Ma[9]在假定地震子波已知的前提下，使用模拟退火算法实现了单道非线性波阻抗反演； Hamid等[10]同样在地震子波已知的假设条件下，在对数域对反演问题线性化，使用Tikhonov正则化方法同时对多道数据进行波阻抗反演。实际上，Tikhonov正则化方法使目标函数的解过度光滑，无法满足地质构造复杂的情况[11]。

本文充分利用地下岩石波阻抗的分布特征、地震子波褶积矩阵的Toeplitz结构以及地震子波的光滑性建立约束条件。全变分(TV)约束可以在压制随机噪声的同时很好地保持地层的边界特征[3]。对子波褶积矩阵进行稀疏矩阵分解可以得到地震子波的稀疏表达[12]。由于地震资料的低频损失，无法反演出波阻抗的低频背景，故将测井或解释层位信息通过最小二乘法建立约束条件[3]。建立的约束最优化目标函数通过基于褶积模型的迭代反演方法求解波阻抗。

由于建立的约束最优化目标函数是非凸的，求解困难，文中采用了对阻抗剖面和子波交替更新求解的策略，将非凸优化问题退化为两个凸优化问题分别求解，有效降低了求解难度[13]。本文将地震剖面整体处理，反演结果比常规的逐道反演具有更好的横向连续性和抗噪能力。

2 波阻抗的全变分(TV)正则化约束

在二维条件下，假设反射系数剖面和波阻抗剖面分别为

(1)

R、Z满足

(2)

可引入变量

(3)

则有

R=L1X

(4)

其中

(5)

因此，地震记录的褶积模型可表示为

D=WL1X+N

(6)

式中：D为地震记录；W为n×n维地震子波褶积矩阵;N为n×m维加性噪声。

波阻抗反演的目的就是在地震记录D已知的条件下求解X，再通过指数运算得到波阻抗剖面Z。最直接的方法是直接求解式(6)中的X

即

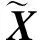
(7)

式(7)是一个病态问题，无法得到适定的解[14]。为得到适定解，对X进行全变分正则化约束，全变分约束可以在压制噪声的同时保持阻抗剖面边界的不连续性[3]，得到

(8)

式中：ε为噪声水平； ‖D-WL1X‖2F≤ε是最基本的最小二乘约束； F为范数； ‖X‖TV是全变分约束。

地震资料的低频损失导致无法反演出波阻抗的低频背景，故将测井或解释层位信息以最小二乘约束‖L2X-Xlow‖2F作为约束条件，L2为低通滤波算子，Xlow为常用对数阻抗低频背景。引入拉格朗日乘子λ1、λ2，将约束最优化问题转换为无约束最优化问题，建立目标函数

‖D-WL1X‖2F+λ1‖X‖TV+

λ2‖L2X-Xlow‖2F

(9)

上述波阻抗反演方法的不足之处在于首先需要提取比较精确的子波，步骤繁琐[15]。

3 Toeplitz结构的稀疏矩阵分解

子波褶积矩阵W具有Toeplitz矩阵结构[12]，对于一般的W做如下分解

即

W=wn-1In-1+…+w1I1+w0I0+w-1I-1+

(10)

式中矩阵I为一系列相应的斜对角矩阵。令向量a=[wn-1,wn-2,…,w0,…,w-(n-2),w-(n-1)]T

目标函数可修改为

λ1‖X‖TV+λ2‖L2X-Xlow‖2F

(11)

实际地震子波长度l远远小于记录长度n，即(l≪n)。地震子波的褶积矩阵为[12]

(12)

对于向量a而言，只有w0,w1,…,wl-1为非零值，其他元素均为0。表明向量a同样具有稀疏性，可以用L1范数作为约束条件。约束最优化目标函数改进为

λ2‖L2X-Xlow‖2F+λ3‖a‖1

(13)

考虑到地震子波在一定程度上还具有光滑性[12]，依然可以作为反演的约束条件。光滑性可以用差分系数的稀疏性来衡量，给目标函数加入以下形式的惩罚项

|ak-ak-1|=λ4‖L3a‖1

(14)

其中

L3[(2n-2)×(2n-1)]

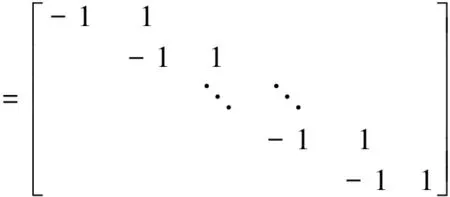
目标函数可改进为

λ2‖L2X-Xlow‖2F+λ3‖a‖1+λ4‖L3a‖1

(15)

求解式(15)是极其困难的，因为该问题属于非凸优化问题。如果固定a或者X中的其中一个，则非凸优化问题退化为一个凸优化问题。可以采用交替固定变量的方法逐步迭代求解原问题[12]。

首先，固定子波褶积矩阵W，问题退化为

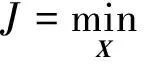
‖D-WL1X‖2F+λ1‖X‖TV+

λ2‖L2X-Xlow‖2F

(16)

同样，若固定X，则问题退化为

λ4‖L2a‖1

(17)

为了方便求解式(17)，将式(17)整理为

(18)

综上所述，通过不断交替更新子波矩阵W和X，直到得到满意的结果。最开始固定的是W，需要一个初始子波。本文方法在大多数情况下直接以地震资料频谱的质心频率为主频的零相位雷克子波作为初始子波就可以得到满意的结果。

上述过程得到对数波阻抗剖面X，利用式(19)可得到波阻抗剖面

Z(i,j)=e2X(i,j)

(19)

4 模型测试

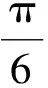
图1 不含随机噪声模型反演结果

为了测试反演方法的抗噪性，在合成记录中加入5%的随机噪声得到正演地震剖面。图2为含随机噪声5%模型反演结果。可以看出，与无噪声反演结果对比，阻抗剖面的横向连续性较强，但阻抗值在层内出现微小的扰动(尤其图2c中的第5层和第7层)。但对于阻抗剖面整体而言，这种微小扰动完全不影响判断地下岩性及其空间展布。反演地震子波与实际地震子波波形差别较小(图2e)。

图2 含随机噪声5%模型反演结果

图3 含随机噪声10%模型反演结果

上述结果表明，在弱噪声条件下，文中的反演方法可以得到相对精确的阻抗剖面。合成记录加入10%的随机噪声得到地震剖面。图3为含随机噪声10%模型反演结果。可以看出，对数阻抗剖面依然保持相对良好的横向连续性，但阻抗值受噪声影响较大，反演结果与给定模型(图1a)有显著区别，但阻抗之间的相对大小并未发生太大变化。由图3d可见，反演的子波与实际波形有较大差别，这是由于受随机噪声的影响。

综上所述，通过反演含有不同强度随机噪声的模型发现，本文方法在随机噪声强度小于约6%的情况下，可以反演出相对精确的阻抗剖面，提取的地震子波波形与给定子波一致性较好。当随机噪声强度接近10%时，反演阻抗剖面的局部稳定性变差，但反演结果保持了较好的横向连续性，依然可以提取到相对准确的地震子波，反演阻抗剖面可以反映地下岩性及其空间展布。

5 实际资料处理

图4是A区实际资料叠加剖面，该剖面过KE031井和JI14井，假设地震资料已经实现吸收衰减等补偿(Q=∞)[18],分别截取黄色方框内剖面作为本次反演的原始数据。图5是图4中黄色区域内截取的地震剖面(图5a、图5b分别是KE031井和JI14井的过井剖面)，分别提取测井曲线的低频部分作为反演的低频背景[19](图6)。图7为图5数据不同方法反演的波阻抗剖面。可以看出，本文方法反演的波阻抗剖面界面连续性更好，薄层分辨率更高(图7c、图7d)。为了验证方法的可靠性，分别将KE031井和JI14井的测井曲线标定在反演剖面上，如图7中的黑色曲线所示。可以看出，本文方法反演的波阻抗剖面与测井曲线更加吻合，可以提高地下岩性和薄层的识辨能力[20-22]。图8为本文方法同步反演的地震子波，初始子波为主频为28Hz(根据地震资料确定)的零相位雷克子波。可以看出，反演子波与初始子波波形基本吻合。

图6 图5数据的低频背景

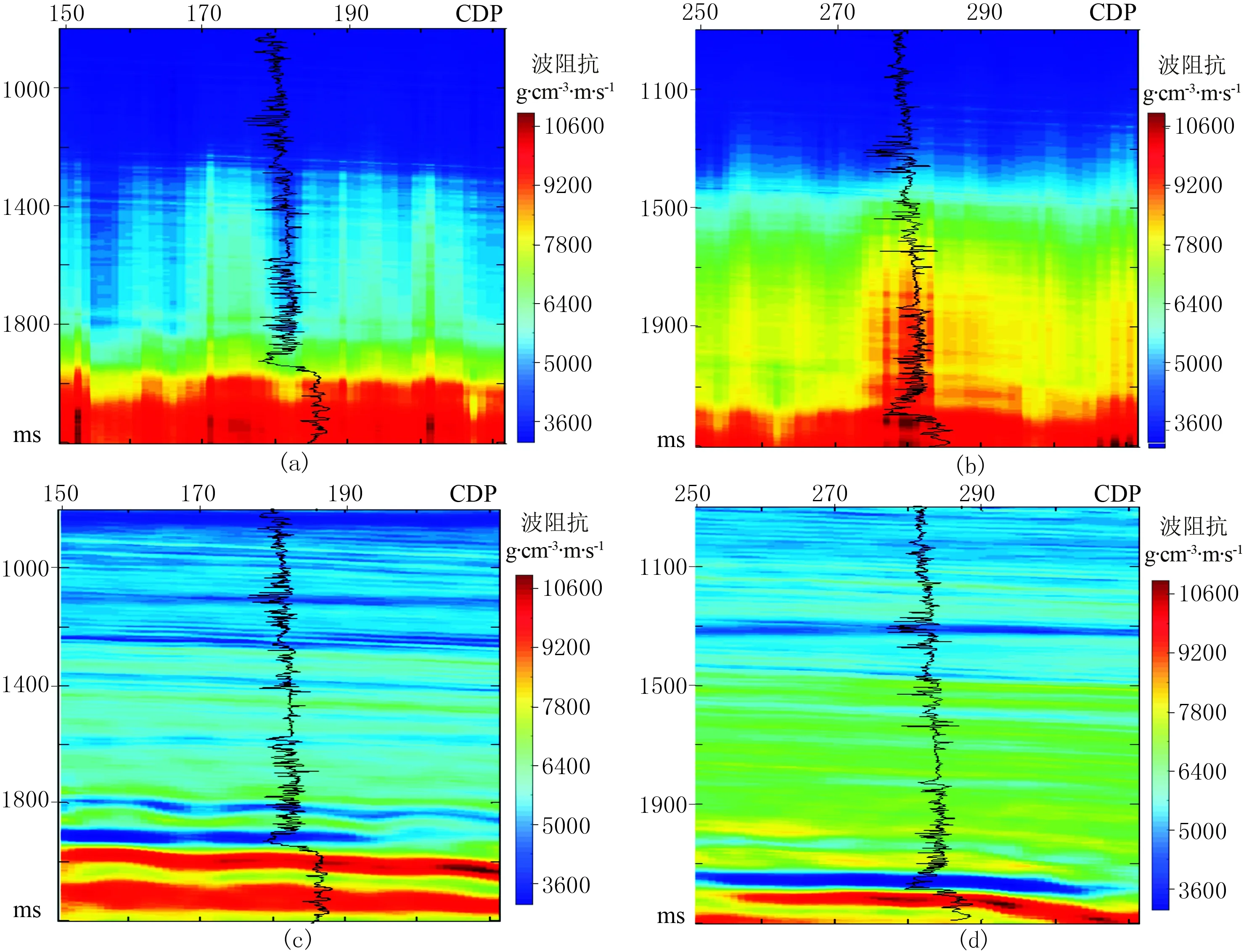
图7 图5a(左)及图5b(右)数据不同方法反演结果对比

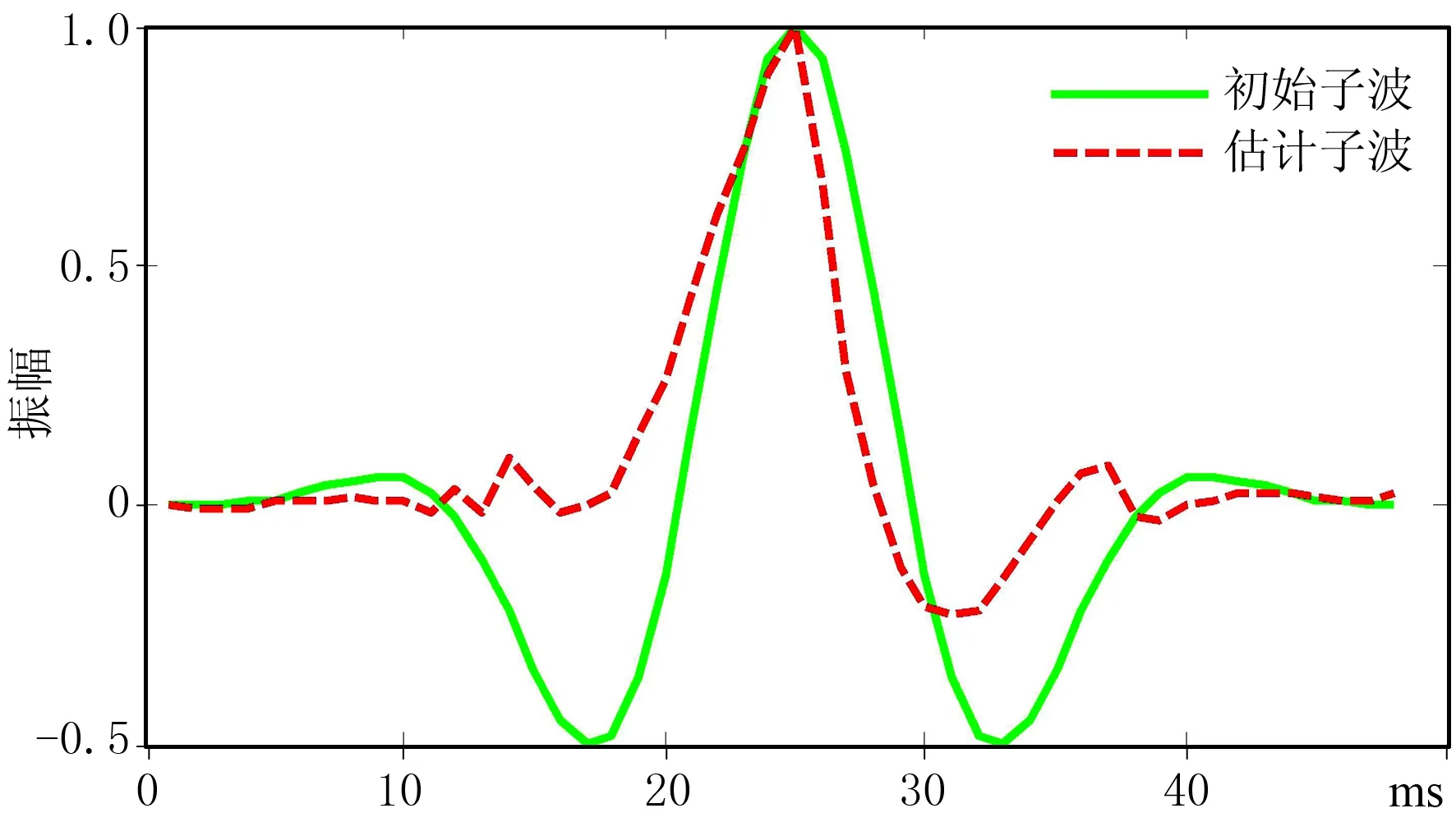
图8 本文方法反演的地震子波

6 结论

本文提出的基于TV约束和Toeplitz矩阵分解的波阻抗反演与常规波阻抗反演相比，主要有以下几点创新和优势。

(1)将子波提取与波阻抗反演合并为一个问题，建立并求解约束最优化目标函数，直接从地震资料中求取地震子波和波阻抗。

(2)利用地震子波褶积矩阵的Toeplitz结构特征，运用稀疏矩阵分解[12]对原地震子波的褶积矩阵进行分解及重构，将地震子波的光滑性及连续性作为约束条件。

(3)利用全变分约束(TV)可以在压制随机噪声的同时很好刻画阻抗剖面的边界特性，保持其不连续性的特点。由于地震资料的低频损失，直接反演出的结果只代表实际阻抗的中频成分，文中设计滤波算子利用最小二乘原理将测井信息作为约束条件。

(4)直接求解建立的目标函数为非凸优化问题非常困难。通过交替固定地震子波和对数阻抗剖面，将一个非凸优化问题退化为两个凸优化子问题，降低了求解难度。

本文方法的不足之处在于该反演方法基于多道处理，受计算机内存限制，无法同时进行较大数据量的运算。

[1] 撒利明,杨午阳,姚逢昌等.地震反演技术回顾与展望.石油地球物理勘探,2015,50(1):184-202.

Sa Liming,Yang Wuyang,Yao Fengchang et al.Review and expectation of seismic inversion technology.OGP,2015,50(1):184-202.

[2] 吕铁良.波阻抗约束反演中的约束方法研究[学位论文].山东青岛：中国石油大学,2007.

Lü Tieliang.Constraint Method Research in Impe-dance Inversion[D].China University of Petroleum,Qingdao,Shandong，2007.

[3] Gholami A.Nonlinear multichannel impedance inversion by total-variation regularization.Geophysics,2015,80(5)：R217-R224.

[4] 彭传平.宽带约束反演方法实现及应用研究[学位论文].陕西西安：长安大学,2008.

Peng Chuanzhen.Broadband Constraint Inversion Method and Application Research[D].Chang’an university,Xi’an,Shaanxi,2008.

[5] 王圣川.正则化约束稀疏脉冲地震反演方法及应用研究[学位论文].四川成都：电子科技大学,2014.

Wang Shengchuang.Regularization Constraint Sparse Pulse Seismic Inversion Method and Application Research[D].University of Electronic Science and Technology of China,Chengdu,Sichuan，2014.

[6] 王东燕.地震约束波阻抗反演及应用研究[学位论文].陕西西安：长安大学,2006.

Wang Dongyan.Impedance Inversion Based on Seismic Constraint and Application Research[D].Chang’an University,Xi’an,Shaanxi，2006.

[7] 裴云龙.稀疏约束反褶积及其波阻抗反演方法研究[学位论文].北京：中国地质大学(北京),2009.

Pei Yunlong.Sparse Constraint Deconvolution and Wave Impedance Inversion Method Research[D].China University of Geosciences(Beijing),Beijing,2009.

[8] Cooke D A and Schneider W A.Generalized linear inversion of reflection seismic data.Geophysics,1983,48(6):665-676.

[9] Ma X Q.A constrained global inversion methon using an overparameterized scheme:Application to post-stack seismic data.Geophysics,2012,66(2):613-626.

[10] Hamid H and Pidlisecky A.Multitrace impedance inversion with lateral constraints.Geophysics,2015,80(6):M101-M111.

[11] Gholami A.A fast automatic multichannel blind seismic inversion for high-resolution impedance recovery.Geophysics,2016,81(5):V357-V364.

[12] Wang Lingling,Zhao Qian,Gao Jinghuai.Seismic sparse-spike deconvolution via Toeplotz-sparse matrix factorization.Geophysics,2016,81(3):V169-V182.

[13] 印兴耀，曹丹平,王宝丽等.基于叠前地震反演的流体识别方法研究进展.石油地球物理勘探,2014,49(1):22-34.

Yin Xingyao,Cao Danping,Wang Baoli et al.Research progress of fluid discrimination with prestack seismic inversion.OGP,2014,49(1):22-34.

[14] Gholami A,Sacchi M D.Fast 3D blind seismic deconvolution via constrained total variation and GCV.Society for Industrial and Applied Mathema-tics,2013,6(4):2350-2369.

[15] 孙学凯,冯世民.地震反演系统中的子波提取方法.物探化探计算技术,2010,32(2):120-125.

Sun Xuekai,Feng Shimin.Wavelet extraction methods of seismic inversion system.Geophysical Computing Technology,2010,32(2):120-125.

[16] 朱卫星,杨玉卿,赵永生等.测井地震联合反演在地质导向风险控制中的应用.石油地球物理勘探,2013,48(增刊1):181-185.

Zhu Weixing,Yang Yuqing,Zhao Yongsheng et al.Joint inversion of logging and seismic data for geosteering risk control.OGP,2013,48(S1):181-185.

[17] Dai Ronghuo,Zhang Fanchang and Liu Hanqing.Seismic inversion based on proximal objective function optimization algorithm.Geophysics,2016,81(5):R237-R246.

[18] 吴华.地震储层反演方法研究及应用[学位论文].北京：中国地质大学(北京),2015.

Wu Hua.Research and Application of Seismic Reservoir Inversion method[D].China University of Geosciences(Beijing),Beijing,2015.

[19] 栾颖.约束稀疏脉冲波阻抗反演方法在煤层识别中的应用[学位论文].吉林长春：吉林大学,2010.

Luan Ying.Constrained Sparse Pulse Wave Impe-dance Inversion Method in the Application of the Coal Seam Recognition[D].Jilin University,Changchun，Jilin,2010.

[20] 张国伟.叠后波阻抗反演及储层预测[学位论文].四川成都：成都理工大学,2014.

Zhang Guowei.Poststack Wave Impedance Inversion and Reservoir Prediction[D].Chengdu Univerisity of Technology,Chengdu，Sichuan，2014.

[21] 杨立强.测井约束地震反演综述.地球物理学进展,2003,18(3):530-534.

Yang Liqiang.Well logging constrained seismic inversion reviewed.Progress in Geophysics,2003,18(3)：530-534.

[22] 石艳玲，黄文辉，魏强等.电磁井震约束反演识别川中深层裂谷.石油地球物理勘探,2016,51(6):1233-1240.

Shi Yanling,Huang Wenhui,Wei Qiang et al.Identify deep rift in central Sichuan via inversion with constraint of electromagnetic and well-seismic.OGP,2016,51(6):1233-1240.

*北京市昌平区府学路18号中国石油大学(北京)地球物理与信息工程学院，102249。Email:529433961@qq.com

本文于2016年10月28日收到，最终修改稿于2017年8月27日收到。

1000-7210(2017)06-1193-07

王治强，曹思远，陈红灵，孙晓明，樊平.基于TV约束和Toeplitz矩阵分解的波阻抗反演.石油地球物理勘探，2017,52(6):1193-1199,1245.

P631

10.13810/j.cnki.issn.1000-7210.2017.06.009

(本文编辑：金文昱)