基于测井约束的地震全波形反演方法

2017-12-18杜泽源吴国忱王玉梅

石油地球物理勘探 2017年6期

关键词：先验测井反演

杜泽源吴国忱王玉梅

(①中国石油大学(华东)地球科学与技术学院，山东青岛 266580； ②海洋国家实验室海洋矿产资源评价与探测技术功能实验室，山东青岛 266580； ③中国石化胜利油田物探研究院，山东东营 257022)

·偏移成像·

基于测井约束的地震全波形反演方法

杜泽源*①吴国忱①②王玉梅③

在实际应用中全波形反演依赖于初始速度模型与低频信息，若初始模型精确度低常会引起周波跳跃现象。测井资料具有垂向分辨率高的特点，含有丰富的超低频与高频成分，测井信息的引入可以在一定程度上弥补地震频带缺失、反射数据精度低、信噪比低的不足，故从两个方面将先验信息引入全波形反演。一是充分利用可靠的测井数据低频信息建立较精确的初始速度模型，以弥补地震数据缺少低频信息的问题；二是在全波形反演目标泛函中引入先验模型约束项，利用测井数据约束反演过程，驱使反演沿给定的方向进行，以提高反演过程的稳定性，从而获得较高精度的速度模型。通过EAGE推覆体模型对所提方法进行试算，相对不加约束全波形反演结果得到改善；实际地震资料应用结果表明，使用测井约束的反演结果能更清楚地展示砂岩层，具有较高的分辨率，反演效果更好。

全波形反演低频信息测井约束初始模型目标泛函

1 引言

全波形反演是利用观测地震数据反演地球介质地球物理参数的方法，其关键是基于波动方程有限差分的正演模拟技术，由于此方法基于双程波动方程的全解[1]，因此称为全波形反演。Tarantola[2]从波动方程出发，通过波场残差逆时传播计算梯度方向，提出基于最小二乘理论的时间域全波形反演理念，奠定了全波形反演的基础。全波形反演最早在时间域实现，Petrick等[3]给出了较为完整的全波形反演定义，随后，Pratt等[4,5]将其发展到频率域，Shin等[6]将其推广到Laplace域。全波形反演技术已被证明是建立高精度速度模型的有效方法[7,8]，得到的速度模型可用于改善深度偏移的质量，进而提供非常有价值的成像结果。全波形反演以减小模拟波场与实际观测波场数据之间的残差为目标，通过最小化目标泛函反演获得高精度速度模型[2,9]。在迭代求解过程中，通过在模型空间寻找梯度和局部下降方向使数据空间的最小二乘目标泛函最小，从而获得每次迭代的速度模型更新量[10]，并将更新速度模型作为下一次迭代的输入模型。同时，全波形反演效果受诸多因素影响，可靠的大炮检距数据、低频信息、初始速度模型等是获得较好反演结果的基本保障[11]。

在实际应用中全波形反演仍面临诸多问题[12]，其中一个重要问题是全波形反演依赖于初始速度模型与低频信息[13]。若初始模型精度低常会引起周波跳跃现象，Weibull等[14]认为全波形反演初始速度模型应该尽量接近真实模型以避免周期跳跃，建议采用波动方程代替射线层析方法获得较精确的光滑初始模型。敖瑞德等[15]提出了基于包络的全波形反演初始模型构建方法，可以得到较高精度的初始模型； Gong等[16]提出了时间域逆时偏移的三维全波形反演算法，可以减少反演结果对初始模型的依赖。然而，为了避免对初始模型的依赖，需要尽可能采集含有丰富低频分量的地震数据，并且要求信噪比和保真度足够高[17]，这在实际地震采集中很难达到，因此构建较准确的初始速度模型很有必要。段超然等[18]联合波场重构反演和全波形反演以确保全波形反演在缺少低频信息时仍能稳定收敛；王毓玮等[19]提出了一种降低非线性程度的分步反演策略，在重建背景模型的基础上恢复模型的中、高波数成分。

在实际勘探过程中可获得丰富的先验信息，如声波测井、地质信息等，传统全波形反演一般不考虑先验信息。当观测地震资料缺少大炮检距数据和低频信息时，在大多数情况下反演结果不理想。因此，可以在全波形反演中利用上述先验信息。测井资料具有垂向分辨率高的特点，含有丰富的超低频与高频成分，测井信息的引入可以在一定程度上弥补地震频带缺失、反射数据精度低、信噪比低的不足，故可将测井信息引入初始速度模型建立。全波形反演需要一个平滑的初始模型以避免在迭代初始就陷入局部极小，而测井数据的分辨率较高，具有高精度的速度及可靠的低频信息，利用测井数据的低频信息对初始模型进行约束，可以得到较精确的初始速度模型。另一方面，可以从目标泛函约束的角度引入先验模型信息，但该过程的操作难度较大，常用于AVO反演。吴国忱等[20]在AVO反演过程中加入尺度约束项，以提高反演的稳定性及可靠性；冯国峰等[21]针对二维波动方程，将大范围收敛的同伦方法引入算子参数识别过程，并利用测井资料进行约束反演；Hu等[22]建议在倍增的正则化项中使用先验模型；王守东[23]针对井间地震资料走时层析成像分辨率低、稳定性差的问题，提出了一种井间地震资料成像新方法——全变差正则化波形反演方法(TVWI)；Han等[24]、傅红笋等[25]研究了测井约束下地震波形反演的同伦摄动求解方法；Asnaashari等[26]提出通过测井、地质解释建立先验模型，并使用正则化项和先验模型项扩展反演目标函数，将先验模型用于反演优化过程，约束最小化目标泛函；成景旺等[27]使用基于柯西分布的频率域目标函数，将低频反演结果作为高频反演的初始模型以减少解的非唯一性。模型测试结果表明，上述方法可获得较为可靠的反演速度模型，但很少投入实际应用。

本文从两个方面将先验信息引入全波形反演。一是充分利用可靠的测井数据低频信息建立较精确的初始速度模型，以弥补地震数据缺少低频信息的不足；二是在全波形反演目标泛函中引入先验模型约束项，利用测井数据约束反演过程，驱使反演沿给定的方向进行，以提高反演过程的稳定性，从而获得较高精度的速度模型。EAGE推覆体模型数据测试及实际地震资料应用结果均证明了文中方法的可行性及有效性。

2 理论方法

2.1 测井约束低频模型构建

鉴于全波形反演对初始模型和低频信息的依赖性，而地震资料由于采集条件的限制，缺少必要的低频数据。通过测井数据约束常规初始速度模型，在常规背景速度场中加入可靠的测井数据低频信息，构建更加精确的初始速度模型，从而避免周波跳跃现象，提高反演精度。

2.1.1 测井资料预处理

测井曲线是地层物理性质随深度变化的记录，包含了高分辨率的地层信息，可以通过测井纵波速度数据提取可靠的低频速度信息。首先要对测井数据进行相应的分析与整理，根据工区的地质背景信息，分析所选测井纵波速度数据，去除奇异值，保证测井数据准确、可靠，然后再进行井震匹配标定，得到准确的时深关系。

实际测井数据一般是深度域的，要想获得测井数据的低频信息，需要把井震标定后的测井曲线进行深时转换，由深度域转到时间域。然后再分析测井数据的频谱特征，并与地震数据的频谱进行对比，综合考虑地质概况，通过适当的滤波方法对测井数据进行滤波处理，得到低频测井曲线。若预先获得的常规初始速度模型是时间域的，则可以在时间域将测井曲线与初始速度模型进行匹配，通过低频测井数据约束得到新的初始速度模型，然后将模型转换到深度域；若常规初始速度模型是深度域的，则需要把时间域的低频测井数据曲线经过时深转换变换到深度域，然后对常规初始速度模型进行深度域约束，得到可直接使用的初始速度模型。图1为模型数据实际测井速度曲线与低频测井曲线。

2.1.2 加权约束模型构建

通过测井数据空间加权约束的方法建立新的初始速度模型。首先，根据工区概况，确定需要参与模型构建的井数及井位信息。将常规方法获得的初始速度模型看成一个三维矩阵，记为Vinitial(x,y,z)，其中x、y、z为模型空间点位坐标。将低频测井数据看成纵向矢量，记为Vwell(xk,yk,z)，其中k=1、2、…、N，N为井的总数，xk、yk为井的水平坐标，图2为测井约束控制示意图。通过测井数据空间加权约束初始速度模型，得到高精度速度模型Vcon(x,y,z)，构建方法通过下式实现

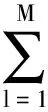
(1)

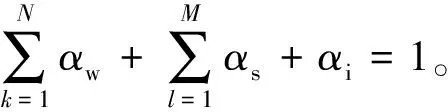
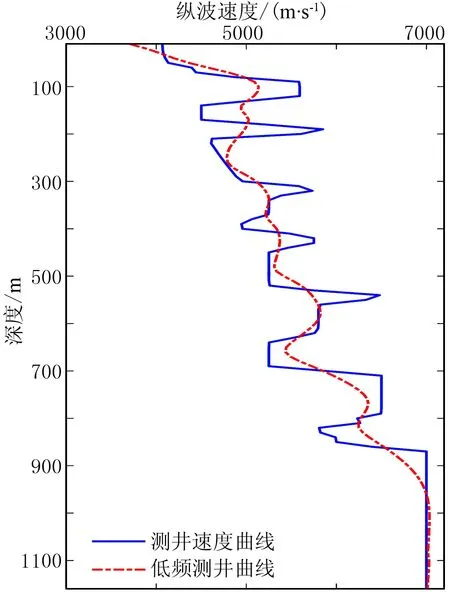
图1 模型数据实际测井速度曲线与低频测井曲线

测井约束项的权重是服从Logistic函数形态分布的，则测井约束空间权重因子可以表示为

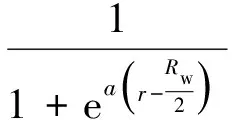
(2)

2.2 测井约束全波形反演方法

通常地球物理反演问题都基于Bayes框架[1]。地震波的正传播过程可抽象表示为

d=G(m)

(3)

式中：m为地球物理参数矢量，如地下地层介质速度、密度或其他弹性参数；d为地震数据；G(m)为基于地层介质模型m的地震波传播过程，描述了地震波场的传播。研究地层介质模型m中地震波传播现象，得到观测地震数据d的过程称为地震波正演，由地震数据d推测地层介质模型参数m的过程称为地震反演。

地震反演过程可以表示为

m=G-1(d)

(4)

全波形反演的误差泛函一般表示为[28]

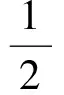
(5)

式中dobs为观测数据。式(5)为最小二乘目标函数。假设观测数据与模型数据服从高斯分布，在目标函数中加入先验模型项，定义含先验模型信息的目标泛函为

(6)

式中：mprior为测井约束的先验模型；λ为权重参数；CD和CM分别为观测数据和模型的协方差。

本文采用梯度引导类方法[29]求解反演问题，梯度引导类方法通过求取目标泛函对模型的导数寻找迭代更新方向。基于声波方程的假设，模型参数为纵波速度场m，观测数据为采集的地震炮集波场dobs，由地震波正演模拟得到的波场为u=G(m)，G表示地震波场正传过程。则误差泛函为

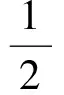
(7)

式中：t为波场传播时间采样点；xr为与炮点xs相对应的检波点坐标。

基于线性化假设，利用变分原理推导泛函梯度，得到泛函对速度模型的梯度为

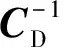
(8)

式中：G*表示波场残差的反传过程；u(t,xs,xr)为炮点xs对应的检波点xr位置的波场。

在反演过程中，权重参数λ的选取是动态的，误差泛函中数据误差项会随着迭代次数的增加而不断减小。因此，为了保证先验模型项与数据误差项对误差泛函贡献的平衡，要求λ随着迭代次数的增加而减小。图3为测井约束全波形反演流程图。

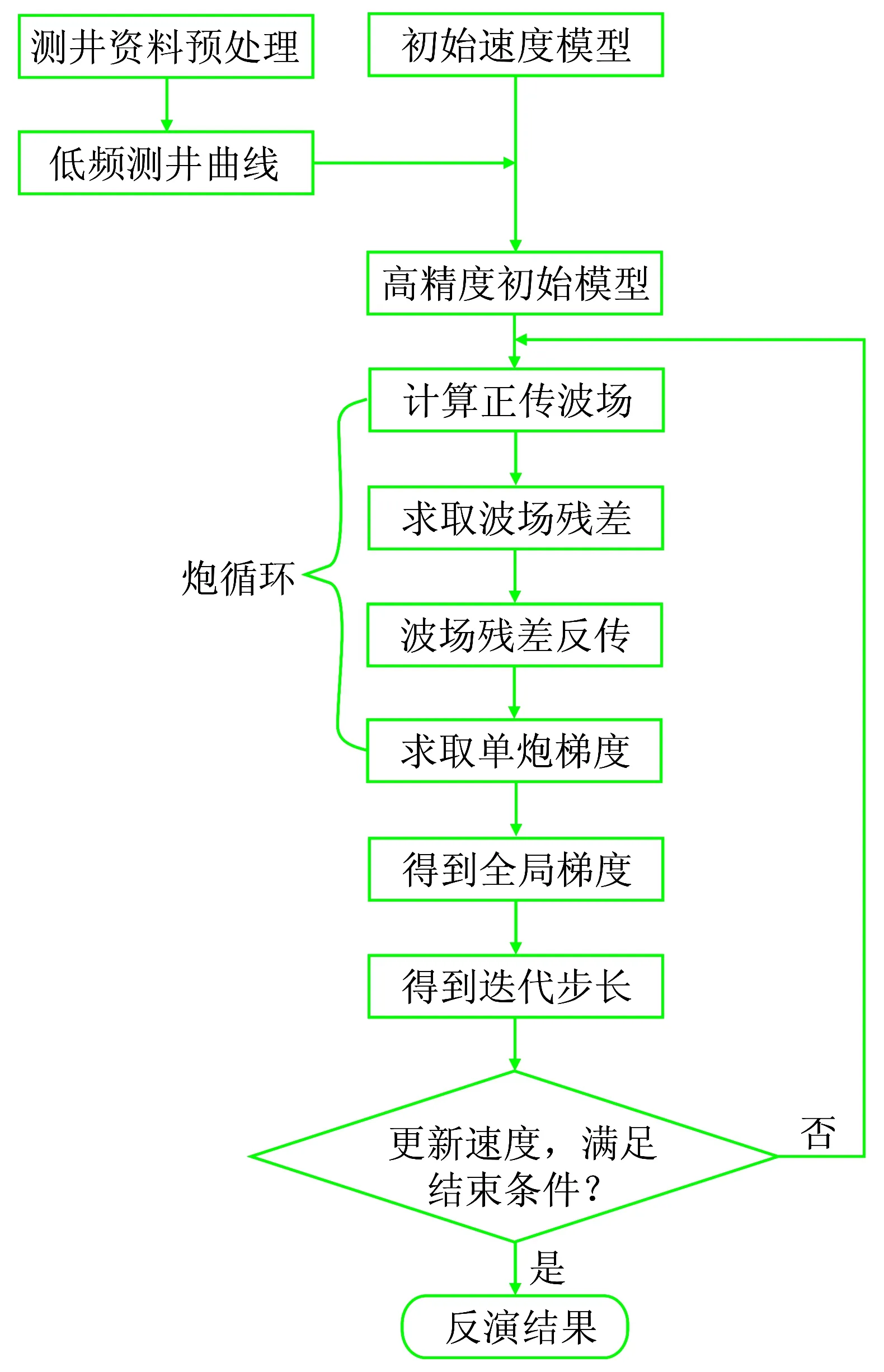
图3 测井约束全波形反演流程图

3 模型试算

本文采用EAGE推覆体模型进行模型试算，抽取600、1400m处垂向单道模型数据作为测井数据(图4a)。

首先，对测井数据进行分析与处理，将测井数据由深度域转到时间域，并分析测井数据与地震记录数据的频谱特征，对测井数据进行滤波处理，得到低频信息，进而将滤波后的时间域测井曲线转换到深度域(图5)。然后根据本文提出的方法，用得到的低频测井数据对常规初始速度模型(图4b)进行加权约束，建立新的基于测井约束的高精度初始速度模型(图4c)。图6为常规初始速度模型曲线与测井约束模型曲线。由图可见，测井约束速度模型依然是一个平滑的模型，其精度比常规初始速度模型高。

图4 真实速度模型、反演初始速度模型及先验模型

图5 实际测井曲线与滤波后低频测井曲线

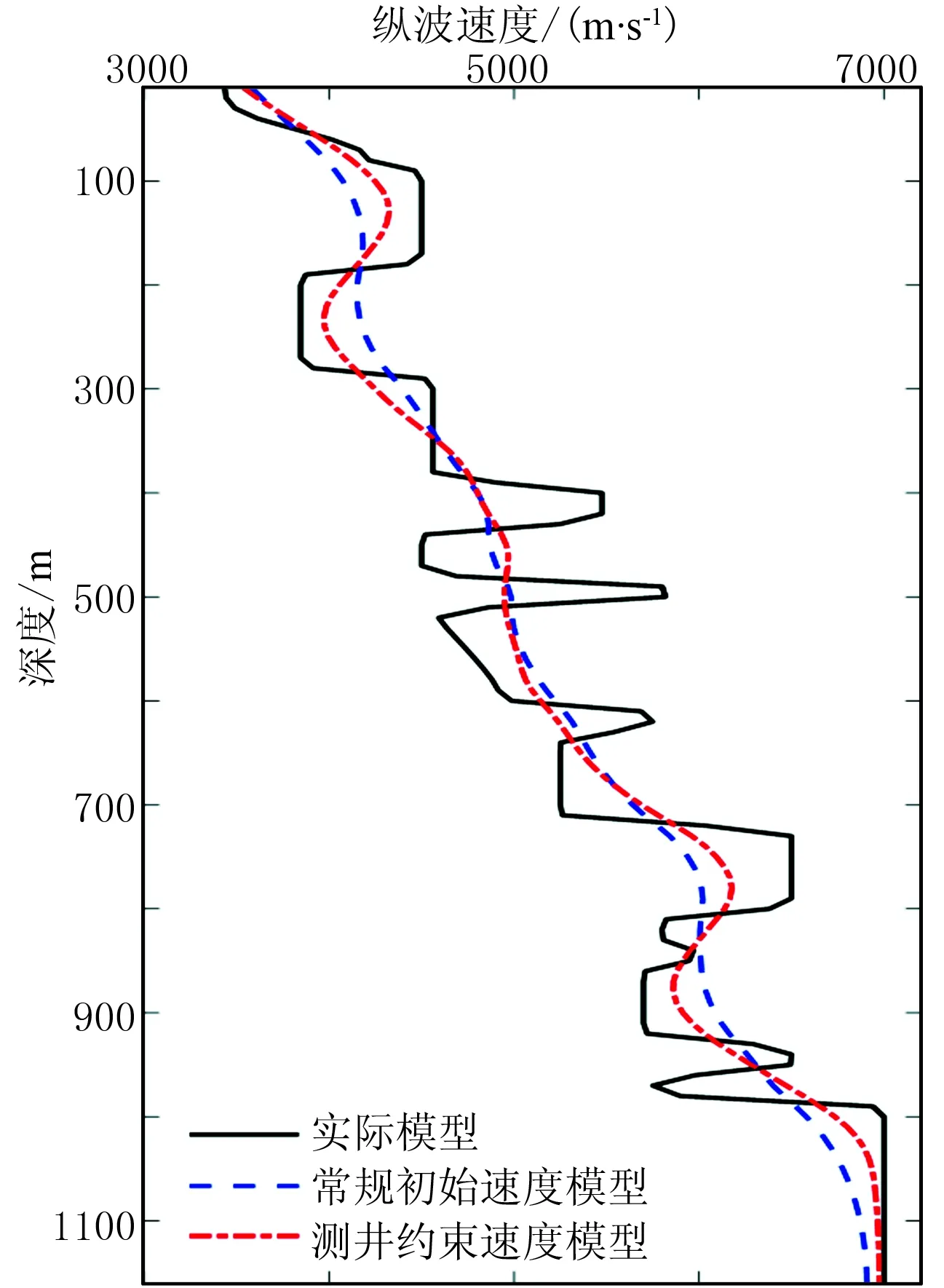
图6 常规初始速度模型曲线与测井约束模型曲线

通过计算测井数据得到测井约束全波形反演的先验模型(图4d)。在水平方向上对井数据进行线性距离加权内插和外推得到插值剖面，然后对其进行轻微的高斯平滑。以平滑后的插值速度作为先验模型约束反演目标泛函，充分利用了测井数据的先验信息，降低了反演陷入局部极小的可能。

为了验证所提方法的反演效果，分别使用常规初始速度模型及本文方法获得的测井约束速度模型进反演。图7为常规初始速度模型反演结果与测井约束反演结果，图8为常规反演与测井约束反演的误差下降曲线。可见测井约束反演方法可以较快地收敛得到最优反演结果。为了更直观地比较两种方法的反演效果，抽取1400m位置处垂向单道速度反演结果进行对比(图9)。可见通过测井约束反演得到的结果更接近真实速度模型，尤其在深层能得到较好的反演结果。

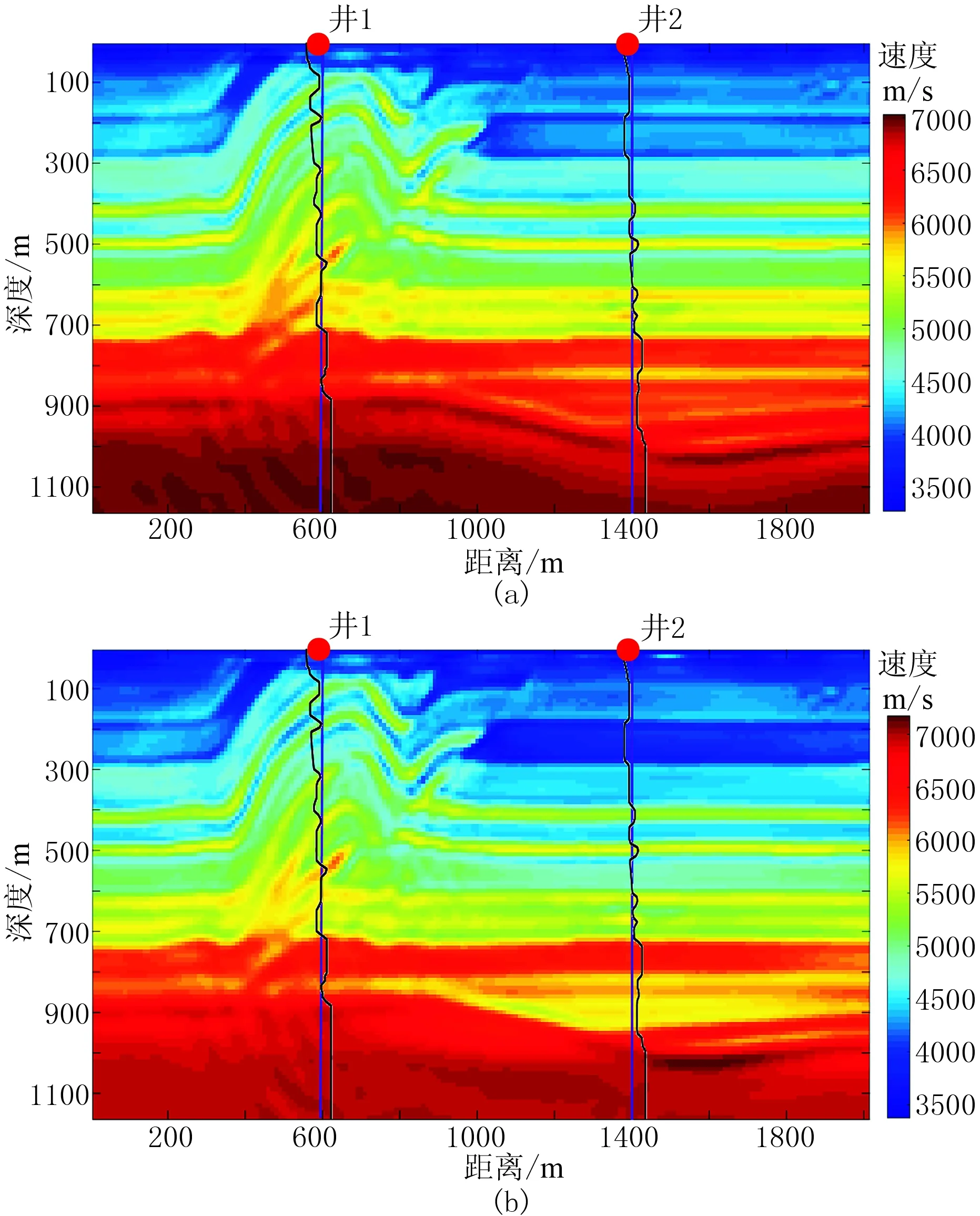
图7 常规初始速度模型反演结果(a)与测井约束反演结果(b)

震源和检波点都位于地表处，共有25炮，第一炮位于10m处，炮间距为80m，第一个检波点位于0处，检波点间隔为10m，地震记录采样间隔为0.0005s，采样点数为1500，总记录时间为0.75s，采用高阶有限差分法进行二维声波正演，理论子波是主频为30Hz的雷克子波

图8 常规反演与测井约束反演的误差下降曲线

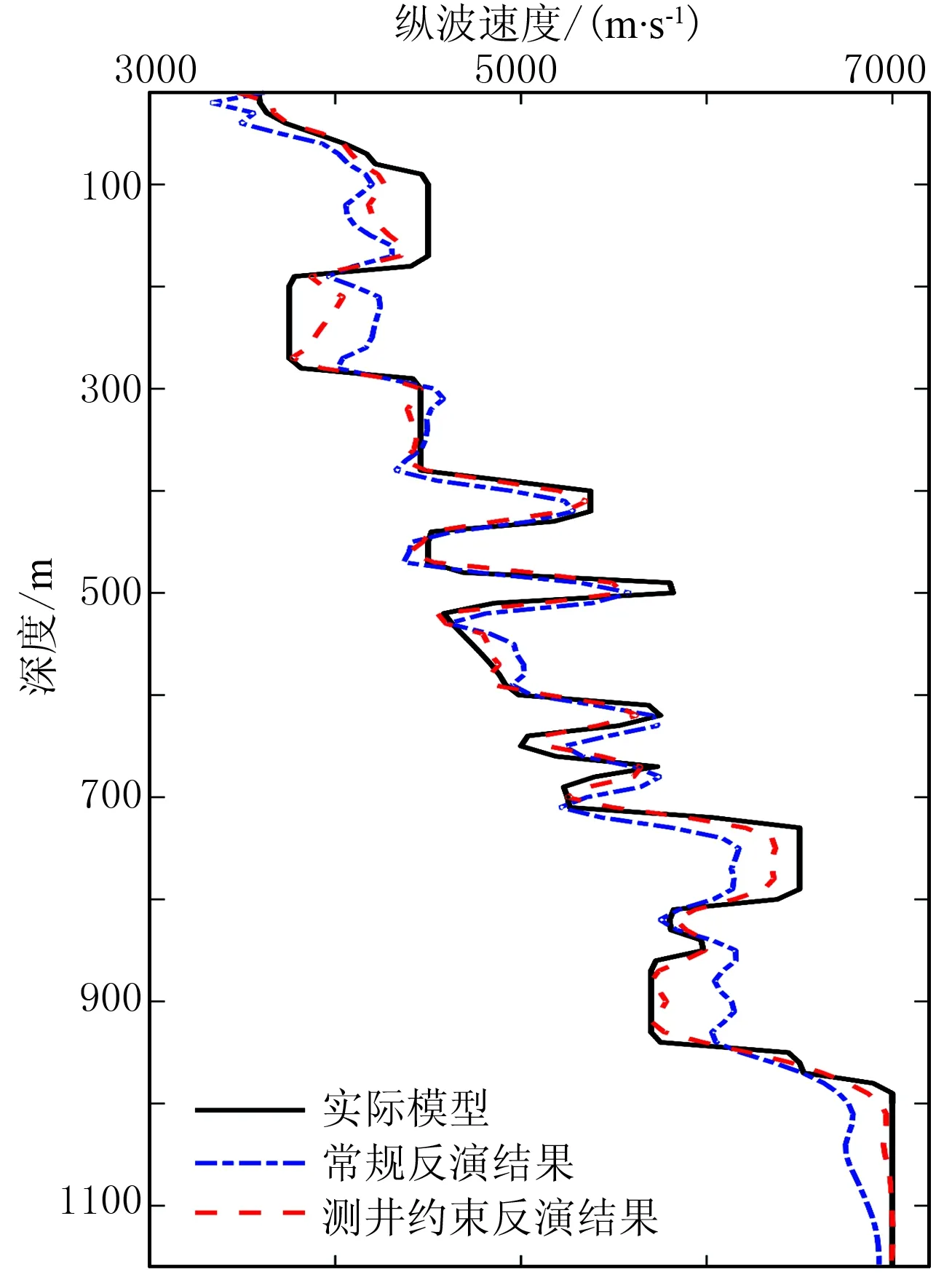
图9 1400m位置处垂向单道速度反演结果

4 实际资料应用

将本方法应用于A工区二维资料。地震资料为一条炮线数据(图10)，反演区域面积为12.45km×4km，初始速度为通过偏移速度分析获得的背景速度场，网格尺寸为10m×10m，在炮线3.55km处有一口探井，测井纵波数据深度范围为1890～3220m。由于该区地震数据带宽有限，低频分量较少，地震数据主频为25Hz，低频信息严重缺失(图12a)。对测井数据进行处理，图11为经过井震标定后的深度域测井数据。根据时深关系，将井曲线由深度域转换到时间域，再对测井数据进行频谱分析，可以看出测井数据既有高分辨率的地层介质速度信息又有丰富的低频分量信息(图12b)。对测井数据进行滤波处理，提取测井数据的低频分量，并选取截止频率为5Hz，在一般情况下截止频率不能取太高，以免在反演一开始就陷入局部极值。图13为时间域测井速度曲线以及滤波后的低频测井曲线。通过时深转换将时间域低频测井曲线变换到深度域。

必须注意到，一般实际测井深度有限，测井数据并非从地表贯穿井底，测井曲线的范围远小于地震资料的时间长度，则低频测井曲线不能完全覆盖研究区域的顶、底界面。如果仅简单地在纵波速度范围对初始速度模型进行校正，则可能在真实井曲线数据范围的顶、底处会产生速度突变，为了防止这一现象，需要对测井数据进行上、下延拓，并逐步在向外延伸区域以常规初始速度为准。图14为测井约束曲线对比。由图可见，低频测井曲线相对于常规初始模型速度更精确，可利用延拓后的低频测井曲线约束常规初始速度模型。

图15为常规初始速度模型与测井约束初始速度模型。由图可见，使用测井约束低频模型构建方法，利用低频测井数据对常规初始速度模型(图15a)进行空间加权约束，可得到测井约束下的初始速度模型(图15b)。

图10 单炮地震记录

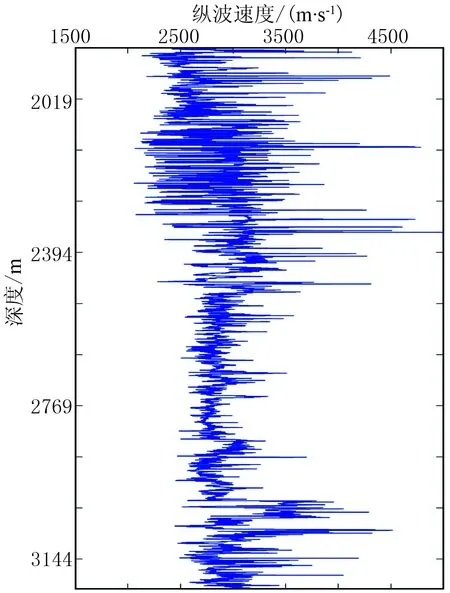
图11 经过井震标定后的深度域测井数据采样间隔为0.125m

图12 地震数据 (a)、测井数据(b)频谱

图13 时间域测井速度曲线及滤波后低频测井曲线对比

图14 测井约束曲线对比

图16为实际数据测井约束反演与常规反演的误差下降曲线。由图可见，利用测井约束全波形反演方法能较快地收敛得到最优结果。图17为常规初始速度模型反演结果与测井约束反演结果。由图可见：由于震源点主要集中于5～7km范围，故模型两侧覆盖次数较低，反演效果较覆盖次数高的区域差；测井解释结果表明，在井位置的3000m深度处存在一套砂岩层(图中黑色箭头所指处)，与常规不加约束的反演结果(图17a)相比，使用测井约束的反演结果能更清楚地展示砂岩层，具有较高的分辨率，反演效果更好(图17b)。

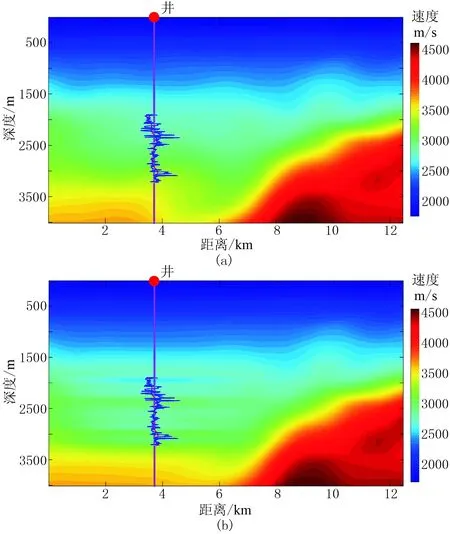
图15 测井曲线附近目标层区域的常规初始速度模型(a)与测井约束初始速度模型(b)

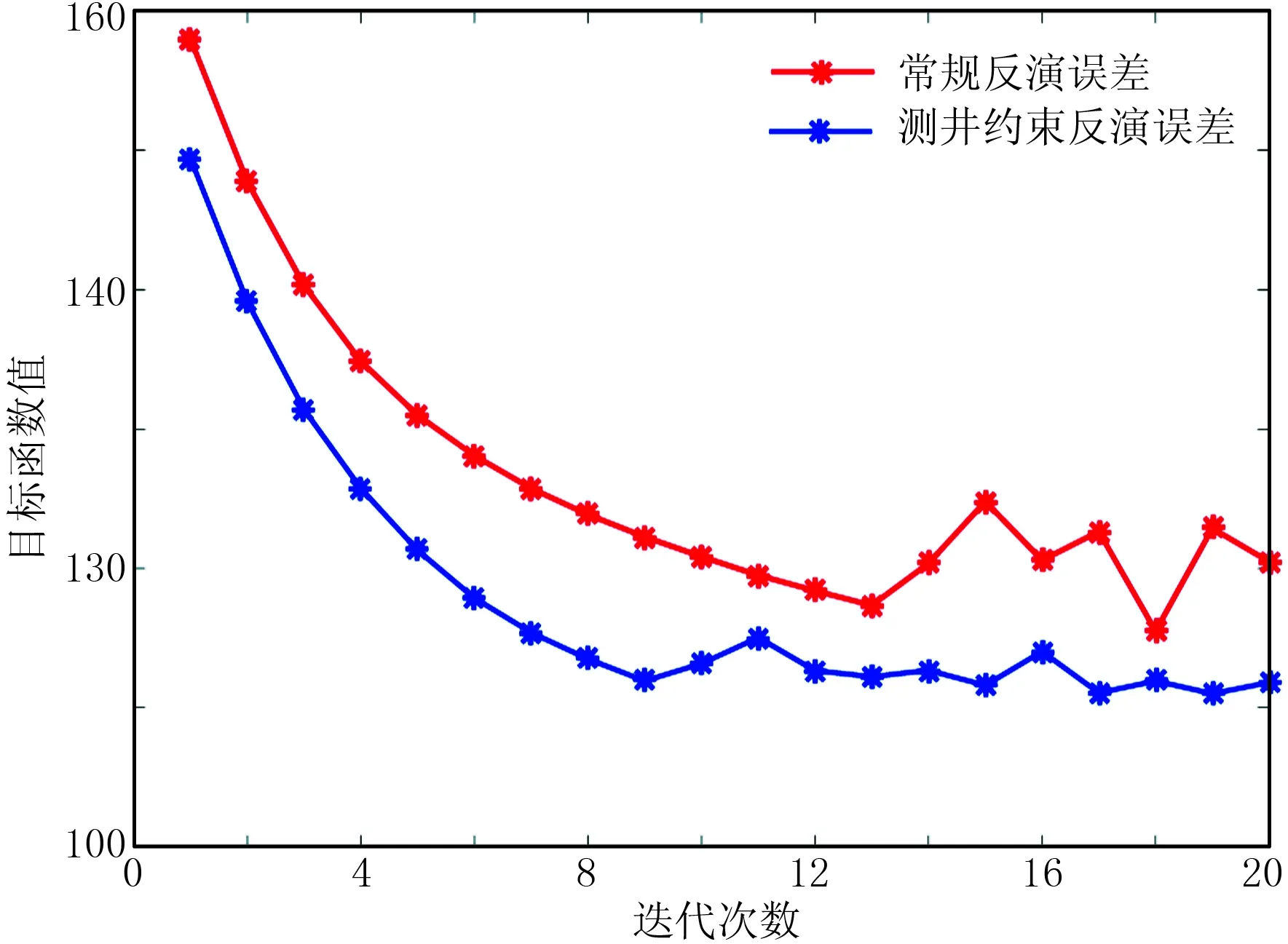
图16 实际数据测井约束反演与常规反演的误差下降曲线

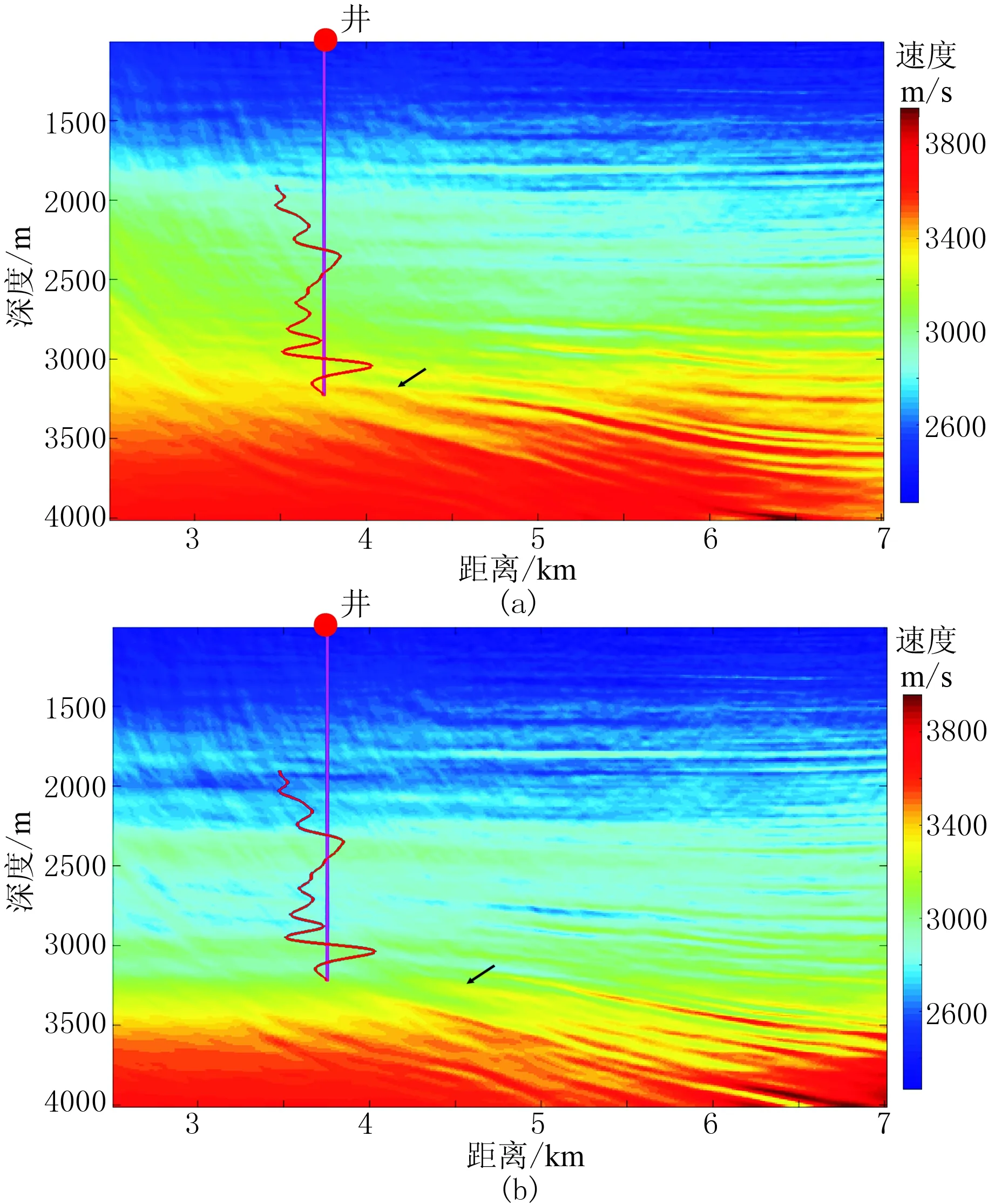
图17 常规初始速度模型反演结果(a)与测井约束反演结果(b)

5 结论与讨论

针对全波形反演对初始模型及低频信息的依赖性，本文研究了基于测井约束的初始模型构建方法及全波形反演方法，在算法实现的基础上，通过模型数据测试证明了文中方法的有效性，并将该方法成功应用于实际地震数据，主要得到以下认识。

(1)由于采集条件的限制，地震数据缺少低频信息。通过提取测井数据中可靠的低频信息可以校正常规初始速度模型中的低频信息，提高初始速度模型的精度。同时，在全波形反演目标泛函中加入先验模型约束项，将测井约束信息引入反演优化过程，可以使反演向着给定的方向进行，避免反演陷入局部极小，可提高反演的稳定性。

(2)测井约束模型构建能在一定程度上提高初始模型的精度，但当构造复杂或地层倾角较大时存在破坏原始构造信息的风险，需要进一步改进模型构建方法。其中权重参数需要随着迭代次数增加动态变化，以防止先验模型项对误差反演贡献过大而在梯度求取中产生新的局部极值，导致反演无法收敛。

(3)模型测试和实际资料应用得到了较好的反演结果，证明了本文方法的有效性。但在实际应用中存在许多亟待解决的问题，如子波的选取、地震资料信噪比等。

[1] Tarantola A.Inverse Problem Theory,Methods for Data Fitting and Model Parameter Estimation.Elsevier Science Publ Co Inc,Amsterdam and New York，1987.

[2] Tarantola A.Inversion of seismic reflection data in acoustic approximation.Geophysics,1984,49(8):1259-1266.

[3] Petrick W R,Borup D T,Steven A J et al.Seismic borehole tomography using full waveform inversion.SEG Technical Program Expanded Abstracts,1988,7:1250-1252.

[4] Pratt R G,Shin C,Hick G J.Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion.Geophysical Journal International,1998,133(2):341-362.

[5] Pratt R G.Seismic waveform inversion in the frequency domain,Part 1:Theory and verification in a physical scale model.Geophysics,1999,64(3):888-901.

[6] Shin C,Cha Y H.Waveform inversion in the Laplace domain.Geophysical Journal International,2008,173(3):922-931.

[7] Sirgue L,Barkved O I,Van Gestel J P et al.3D waveform inversion on Valhall wide-azimuth OBC.EAGE 71st Conference and Exhibition Extended Abstracts,2009.

[8] Warner M,Umpleby A,Stekl I et al.3D full-wavefield tomography:imaging beneath heterogeneous overburden.EAGE 72st Conference and Exhibition Extended Abstracts,2010.

[9] Pratt R G,Song Z M,Williamson P et al.Two-dimensional velocity models from wide-angle seismic data by waveform inversion.Geophysical Journal International,1996,124(2):323-340.

[10] Smithyman B,Pratt G,Hayles J et al.Detecting near-surface objects with seismic waveform tomography.Geophysics,2009,74(6):WCC119-WCC127.

[11] Virieux J,Operto S.An overview of full-waveform inversion in exploration geophysics.Geophysics,2009,74(6):WCC1-WCC26.

[12] 杨午阳,王西文,雍学善等.地震全波形反演方法研究综述.地球物理学进展,2013,28(2):766-776.

Yang Wuyang,Wang Xiwen,Yong Xueshan et al.The review of seismic full waveform inversion method.Progress in Geophysics,2013,28(2):766-776.

[13] Shah N,Warner M,Nangoo T et al.Quality assured full-waveform inversion:Ensuring starting model adequacy.SEG Technical Program Expanded Abstracts,2012,31.

[14] Weibull W,Arntsen B,Nilsen E.Initial velocity models for full waveform inversion.SEG Technical Program Expanded Abstracts,2012,31.

[15] 敖瑞德,董良国,迟本鑫.不依赖子波、基于包络的FWI初始模型建立方法研究.地球物理学报,2015,58(6):1998-2010.

Ao Ruide,Dong Liangguo,Chi Benxin.Source-independent envelope-based FWI to build an initial model.Chinese Journal of Geophysics,2015,58(6):1998-2010.

[16] Gong B,Chen G,Yingst D et al.3D waveform inversion based on reverse time migration engine.SEG Technical Program Expanded Abstracts,2008,27:1900-1904.

[17] Baeten G,Maag J W,Plessix R E et al.The use of low frequencies in a full-waveform inversion and impedance inversion land seismic case study.Geophysical Prospecting,2013,61(4):701-711.

[18] 段超然,韩立国.主成分分析波场重构反演与全波形反演联合速度重构.石油地球物理勘探,2016,51(6):1134-1140.

Duan Chaoran,Han Liguo.A joint velocity reconstruction method:principal component analysis based wavefield-reconstruction inversion combined with full waveform inversion.OGP,2016,51(6):1134-1140.

[19] 王毓玮,董良国,黄超等.降低弹性波全波形反演强烈非线性的分步反演策略.石油地球物理勘探,2016,51(2):288-294．

Wang Yuwei,Dong Liangguo,Huang Chao et al.A multi-step strategy for mitigating severe nonlinearity in elastic full-waveform inversion.OGP,2016,51(2):288-294.

[20] 吴国忱,田军.基于尺度约束项的AVO反演方法.石油地球物理勘探,2014，49(6):1157-1164.

Wu Guochen,Tian Jun.AVO inversion based on scale constraints.OGP,2014,49(6):1157-1164.

[21] 冯国峰,韩波,刘家琦.二维波动方程约束反演的大范围收敛广义脉冲谱方法.地球物理学报,2003,46(2):265-270.

Feng Guofeng,Han Bo,Liu Jiaqi.Widely convergent generalized pulse spectrum methods for 2D wave equation inversion.Chinese Journal of Geophysics,2003,46(2):265-270.

[22] Hu W,Abubakar A,Habashy T M.Simultaneous multifrequency inversion of full-waveform seismic data.Geo-physics,2009,74(2):R1-R14.

[23] 王守东.井间地震资料全变差正则化波形反演.石油物探,2011,50(3):234-240.

Wang Shoudong.Total variation regularization waveform inversion of crosswell seismic data.GPP,2011,50(3):234-240.

[24] Han B,Fu H S,Liu H.A homotopy method for well-log constraint waveform inversion.Geophysics,2007,72(1):R1-R7.

[25] 傅红笋,曹莉,韩波.测井约束地震波形反演的同伦摄动法.地球物理学报,2012,55(9):3173-3179.

Fu Hongsun,Cao Li,Han Bo.A homotopy perturbation method for well log constrained seismic waveform inversion.Chinese Journal of Geophysics,2012,55(9):3173-3179.

[26] Asnaashari A,Brossier R,Garambois S et al.Regularized seismic full waveform inversion with prior model information.Geophysics,2013,78(2):R25-R36.

[27] 成景旺,吕晓春,顾汉明等.基于柯西分布的频率域全波形反演.石油地球物理勘探,2014,49(5):940-945.

Cheng Jingwang,Lü Xiaochun,Gu Hanming et al.Full waveform inversion with Cauchy distribution in the frequency domain.OGP,2014,49(5):940-945.

[28] 任浩然.声介质地震波反演成像方法研究[学位论文].上海:同济大学,2011.

Ren Haoran.A Study of the Seismic Wave Inversion Method for Imaging in the Acoustic Media[D].Tongji University,Shanghai,2011.

[29] Mora P.Nonlinear two-dimensional elastic inversion of multioffset seismic data.Geophysics,1987,52(9):1211-1228.

*山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: duzy10@163.com

本文于2016年10月28日收到，最终修改稿于2017年8月21日收到。

本项研究受国家重大科技专项(2016ZX05024-001-008)资助。

1000-7210(2017)06-1184-09

杜泽源，吴国忱，王玉梅.基于测井约束的地震全波形反演方法.石油地球物理勘探，2017,52(6):1184-1192.

P631

10.13810/j.cnki.issn.1000-7210.2017.06.008