基于威布尔分布的不同地区弹药贮存寿命评估--以催泪弹、爆震弹为例

陈佳欣，郭红霞，刘禄胜



基于威布尔分布的不同地区弹药贮存寿命评估--以催泪弹、爆震弹为例

陈佳欣，郭红霞，刘禄胜

（武警工程大学，陕西 西安，710086）

针对当前武警基层部队在对防暴弹药的管理中存在大量浪费且报废困难的问题，选取海南省、陕西省、吉林省3个地区自然贮存一定时间段的催泪弹、爆震弹试验数据进行统计分析，准确评估了不同地区弹药贮存寿命。首先依据弹药在贮存状态下的失效特点，利用威布尔分布建立贮存可靠性模型，进而通过弹药实测数据，采用极大似然方法估计分布参数，最后在置信度为0.9、可靠度下限分别为0.9、0.85、0.8时，根据模型对不同地区弹药贮存可靠寿命进行预测。结果表明弹药的可靠贮存寿命均超过5a，该结论对武警部队防暴弹药贮存管理具有指导性意义。

催泪弹；爆震弹；贮存寿命；威布尔分布；预估

催泪弹和爆震弹是武警部队广泛采用的非致命性武器，平时必须具有一定量储备。当前基层部队所用该类弹药的一般出厂规定年限为5a，然而到规定年限后弹药的报废成为一大难题，且绝大多数弹药可靠性仍在规定要求之内，造成了大量的浪费。为解决这一问题，笔者选取海南省、陕西省、吉林省3处全年温度、湿度相差较大、具有典型性的地区自然贮存一定时间段的催泪弹、爆震弹试验数据，进行统计分析，即定量分析弹药的贮存可靠寿命问题。

由于弹药在贮存过程中处于非工作状态，贮存环境应力比工作应力小得多，弹药失效往往是长期缓慢的过程[1]。在对贮存多年的弹药进行性能检测后，只能获知所测弹药是否失效，并不能得到弹药失效的具体时间[2]，而且对出厂弹药进行失效控制，一般会造成成品弹药的破环和损失。因此，科学定量地评估弹药贮存寿命，以便准确掌握弹药性能的变化规律和所处状态，对指导弹药贮存管理、减少部队后勤装备损失，具有重要的理论和现实意义。

1 弹药贮存寿命评估方案

1.1 评估步骤

设计如图1所示的可靠性统计分析建模方案。

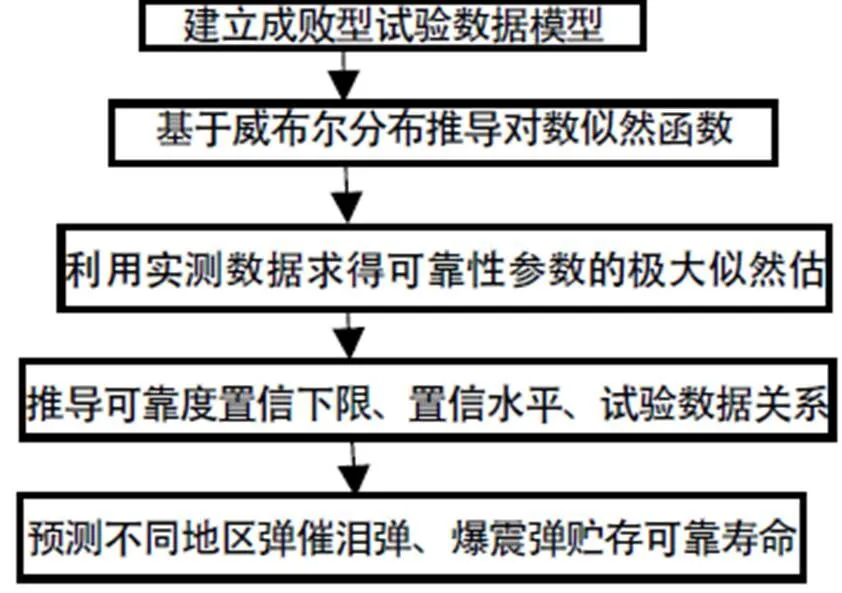
图1 统计建模步骤

1.2 威布尔分布

在弹药贮存可靠寿命问题中，弹药寿命分布可以用很多分布函数描述，例如威布尔分布、逆威布尔分布和极小值分布[3]。其中，由于威布尔分布根据串联模型得到，能充分反映最弱元件对整体性能的影响，故凡是由于局部失效而导致整体机能失效的串联公式模型都可采用威布尔分布[4]。弹药主要是由火工品和各种元件组成，研究认为，弹药贮存寿命服从或近似服从威布尔分布[5]，其分布密度函数为[4]：

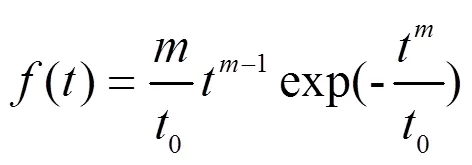
分布函数为：

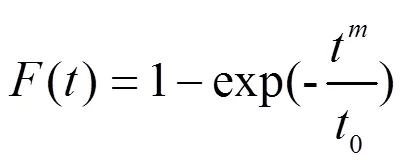
可靠度函数为：

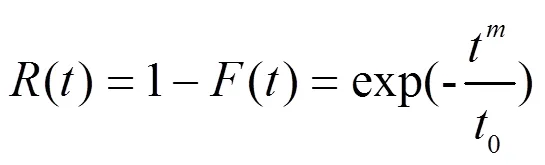
2 模型构建

2.1 试验数据模型

设：对同一批次出厂后贮存相同时间段（）的弹药进行随机抽样，样本量为，实施可靠性试验后显示失效数为，则弹药可靠性试验数据可表示为：（t，n，k），（=1,2,……）。其中，t为弹药贮存时间（年）；n为一次试验所抽取的样本容量（发）；k为样本中出现的失效数（发）；为抽取不同贮存时间段弹药的组次；为抽取不同贮存时间段弹药的组数。

记第组的第个样本的贮存寿命为T(=1,2,……；=1,2……n)，T独立同分布于双参数威布尔分布(t；,0)。由于弹药可靠性测试结果为成败型试验数据[6]，令：

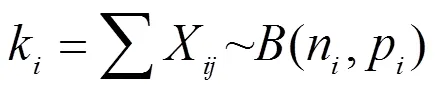
式（5）中：p=(t;,0)，即：每次试验样本中出现的失效数k服从参数为n和p的二项分布。

2.2 参数估计

为确定贮存弹药的可靠寿命分布，需要对分布的参数值进行估计。经大量实例表明，最小二乘法和最大似然法均可用于估计分布的参数值[7]，但最小二乘法效果略逊一筹，故本文采取最大似然估计法。与试验数据(t,n,k)相对应的似然函数为：

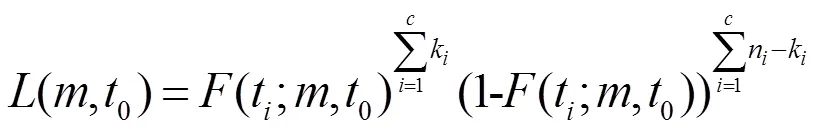
公式（7）的形式难于处理，将其取对数，则可得对数似然函数：

将双参数威布尔分布函数公式（2）代入公式（8），可得对数似然函数：

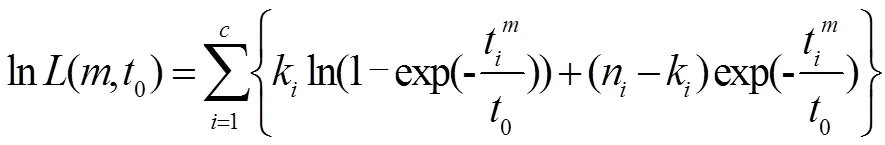
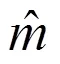
2.3 可靠寿命TR预测

在(1-)置信水平下，可靠度置信下限由式（10）确定，即：

式（10）中R表示弹药可靠度下限。式（10）表明：R不会低到使事件“出现k个或比k个失效数目还少”的概率值低于小概率（取=1）；取可靠度下限值R分别为0.9、0.85、0.8。

结合公式（3），即双参数威布尔分布的可靠度函数，可以得到威布尔分布下可靠寿命T的估计值[8]：

3 实例分析

3.1 试验实施

3.1.1 试验要求

要求一次试验中每个检测年份上抽取的弹药样本均来自同一厂商、同一批次的产品，且要求该批弹药贮存在同一仓库或同地区同库型[8]。进行投射试验时需选择空旷场地，并要求无风无雨无雾等天气。

3.1.2 试验地点

选取沿海高热高湿高盐地区、东北高寒地区，以及内地温带大陆性气候地区等不同典型环境地域贮存的相同品种，且经过相同贮存时间的防暴弹药进行技术检查和试投试射。

3.1.3 试验对象

此次试验选取了吉林总队的长春地区、海南总队的海口地区、西安地区部队贮存的防暴弹药作为试验对象，以38mm枪射催泪弹（QP98-38CS）和手投式爆震弹（WJ）作为试验弹药，抽样同时抽取了地处湿地环境的工厂部份留观弹药产品做对比试验。

3.1.4 试验指标判断

进行试投试射实验时，对催泪弹射出后的起燃时间、发烟时间用秒表进行测试，并在试验后对射程进行测量，对爆震弹投出后的声强用分贝仪进行测量，并着重观察是否瞎火。最终整理数据时，对起燃时间大于10s、发烟时间小于12s、射程小于65m的催泪弹均判断为失效，对声强小于130dB或出现哑弹的爆震弹判断为失效。

3.2 海南省弹药试验分析

3.2.1 催泪弹试验

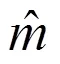
3.2.2 爆震弹试验

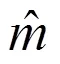
3.3 陕西省弹药试验分析

3.3.1 催泪弹试验

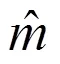
3.3.2 爆震弹试验

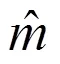
3.4 吉林省弹药试验分析

3.4.1 催泪弹试验

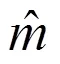
3.4.2 爆震弹试验

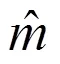
3.5 各地区弹药试验数据及参数汇总（c=3，i=1,2,3）

表1~2分别为各地区催泪弹、爆震弹贮存可靠性试验数据及参数估计，可靠度对比曲线如图2~3所示。

表1 各地区催泪弹贮存可靠性试验数据及参数估计

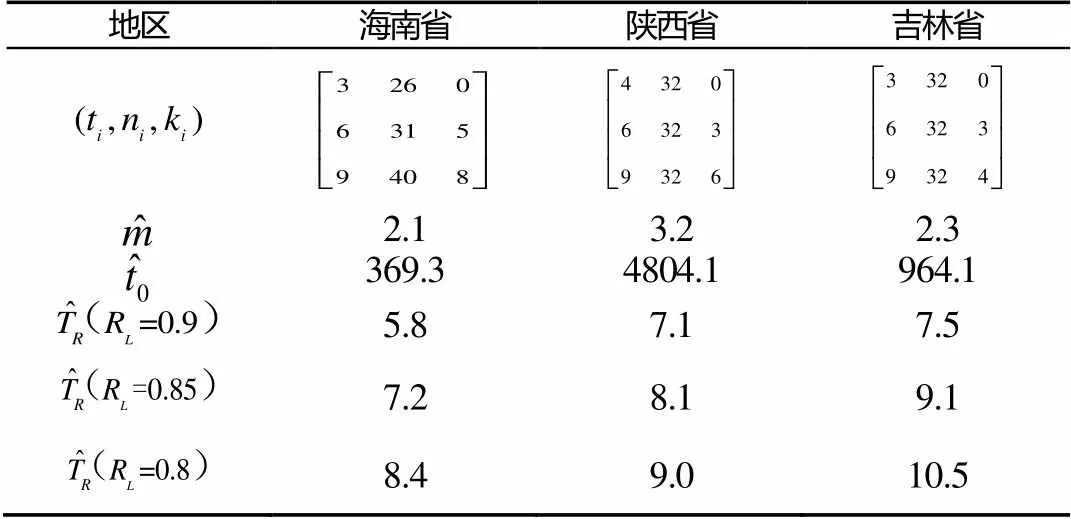
Tab.1 Reliability test data and estimations of storaged tear-gas grenades in different areas

表2 各地区爆震弹贮存可靠性试验数据及参数估计

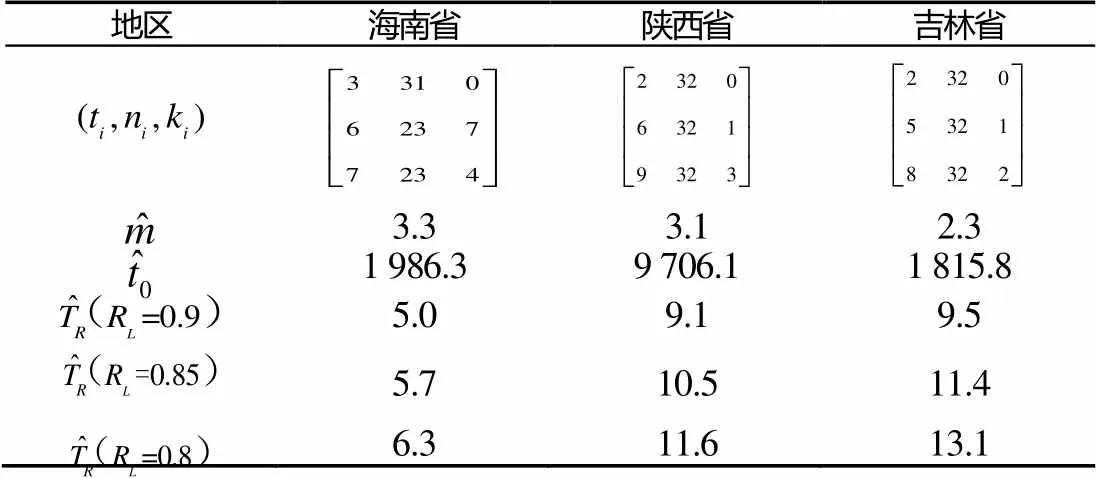
Tab.2 Reliability test data and estimations of storaged stun grenades in different areas

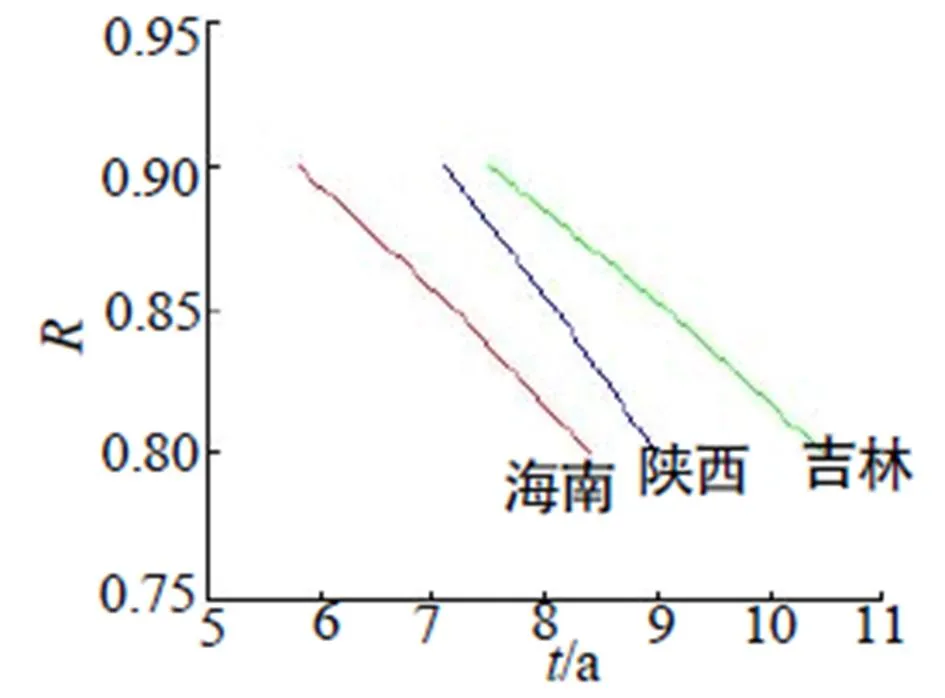
图2 不同地区催泪弹寿命——可靠度曲线图

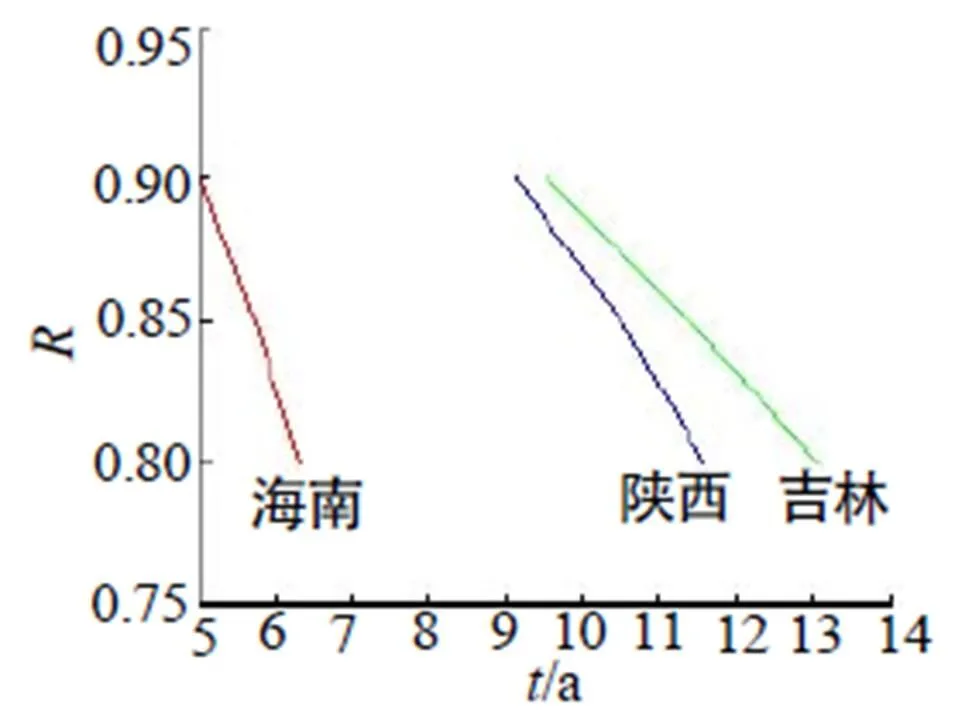
图3 不同地区爆震弹寿命——可靠度曲线图

由表1~2中及图2~3可知，置信度为0.9时，当可靠度下限分别为0.9、0.85、0.8时，不同地区催泪弹及爆震弹的贮存寿命均超过出厂规定的5a年限，且在相同可靠度下，吉林地区的弹药寿命明显长于海南地区，且稍好于陕西地区。

4 结语

本文利用不同地区催泪弹、爆震弹贮存寿命试验数据进行统计分析，建立相应的数学模型，对其贮存寿命进行评估。评估结果显示，尽管在可靠度下限严格取值为0.9的情况下，弹药的最低可靠寿命为5a，且位于吉林地区所贮存的催泪弹、爆震弹寿命预测值显著长于海南，且较好于陕西地区。这表明，武警基层部队所使用的防暴弹药在贮存5a后仍然可以投入使用，没有必要进行全部报废销毁。并据此可以得出如下结论:各个地区，尤其是温度较高、湿度较大的地区，只要改善库存条件，防潮防热，保持密封，就可以保证催泪弹、爆震弹的贮存寿命尽可能延长，达到最佳环境地区的弹药贮存寿命值，从而为弹药质量监控管理提供理论支撑，解决弹药报废耗资费力的难题，且有利于减少部队后勤装备不必要的损失，对现实弹药贮存管理具有指导意义。

[1] 刘金梅,王建萍,张力.生存分析法在弹药贮存可靠性评估中的应用[J].弹箭与制导学报,2004,24(3):332-334.

[2] 马野,董彩霞,张熹涛.舰炮弹药储存可靠寿命计算方法[J].四川兵工学报,2015,36(3):98-101.

[3] 刘传模.弹药可靠性工程基础[M].石家庄:军械工程学院, 1996.

[4] 祝逢春,王晓鸣,崔大伟,姜红波,朱丽娴.航空弹药失效分布拟合方法比较研究[J].弹箭与制导学报,2006,26(2):922-925.

[5] 祝逢春,胡瑜,游培寒,刘传武,沈坚平.基于实际储存使用信息的制导弹药可靠贮存寿命预测[J].弹箭与制导学报,2013, 33(6):197-200.

[6] 郑波,李淦,李明.基于成败型试验数据的弹药贮存寿命评估[J].军械工程学院学报,2005,17(5):29-30.

[7] 高萌,王金柱,何学广.基于可靠性统计分析法的制导弹药储存寿命评估[J].装备环境工程,2013(4):110-114.

[8] 郭红霞,庄弘炜.基于成败型试验的催泪弹贮存寿命评估方法[J].火工品,2008 (6):45-47.

Estimation of Ammo Storage Life in Different Areas Based on Weibull Distribution--Taking Examples of Tear-gas Grenades and Stun Grenades

CHEN Jia-xin, GUO Hong-xia, LIU Lu-sheng

(Engineering University of PAP, Xi’an，710086)

At present, the management of antiriot ammunition in paramilitary police units exits many problems of waste and scraping. This paper chose the testing data of tear-gas grenades and stun grenades, which had been storage in Hainan, Shannxi and Jilin Provinces for certain years, to conducting the statistical analysis. Firstly, according to the failure feature under the storage status, the mathematical model for storage reliability was established, based on Weibull distribution. Then, the actual ammo testing data was utilized to estimate the value of the distribution by adopting the maximum likelihood method. After that, ammo storage life in different areas with the model was estimated, under the confidence coefficient with a value of 0.9 and certain lower confidence limit of reliability with the values of 0.9, 0.85, 0.8. The result showed that the reliable storage life of ammunition is more than five years, which has guiding significance for ammo storage management.

Tear-gas grenade；Stun grenade；Storage life；Weibull distribution；Estimation

1003-1480（2017）05-0054-04

TJ45+9

A

10.3969/j.issn.1003-1480.2017.05.014

2017-07-03

陈佳欣（1991 -），女，在读硕士研究生，主要从事应用统计学研究。

武警部队科研项目。