基于覆盖分割和活动轮廓模型的图像边缘提取算法

2017-12-15顾雨迪梁久祯

数据采集与处理 2017年5期

关键词：轮廓线边缘边界

顾雨迪梁久祯吴秦李敏

(1.江南大学信息化建设与管理中心，无锡，214122；2.江南大学物联网工程学院智能系统与网络计算研究所, 无锡,214122)

基于覆盖分割和活动轮廓模型的图像边缘提取算法

顾雨迪1梁久祯2吴秦2李敏2

(1.江南大学信息化建设与管理中心，无锡，214122；2.江南大学物联网工程学院智能系统与网络计算研究所, 无锡,214122)

针对传统算法对边界模糊的图像分割效果不理想，分割结果多毛刺的问题，提出了一种由粗到细的图像边缘提取方法，主要由像素覆盖分割方法和Chan-Vese模型组成。将改进的覆盖分割方法和活动轮廓模型相结合，首先使用原始覆盖分割算法对图像进行分割，利用多方向模糊形态学边缘检测算法提取不同物体之间的边界；然后采用改进的像素覆盖分割方法给边界像素重新分配覆盖值；最后，运用活动轮廓算法进行细化的图像边界提取；分别进行了分割结果的定性比较，抗噪性测试以及提取的边缘对比实验。实验结果表明，该方法对具有模糊边界的图像，提取边缘结果优于其他可比文献中提出的方法。

边缘提取；覆盖分割；Chan-Vese模型

引言

图像分割是分析图像的第一步，是计算机视觉和图像处理领域中的一个基础性难题[1]。图像分割就是根据需求将图像分成许多轮廓，其中每个轮廓具有独特性质，可根据轮廓提取出有意义和有价值的特征[2]。图像处理过程中最重要且最具有意义的就是图像边界的划分[3]，因为它会影响图像分割的最终结果。至今为止，各种各样的用来解决图像分割难题的算法已被提出[4]。研究人员还做了很大的努力来改善图像分割算法的性能。最近，一些集中在模糊离散对象的研究被提出。Lindblad等[5-7]利用覆盖模型提高估计精度。Sladoje等[8,9]基于任意现有的清晰分割，并通过确定边界像素重新评估它们的覆盖值，提升为覆盖细分。与其他模糊表达相比，覆盖模型的优势来自明确定义的隶属函数，可以利用这些假设推导出估计误差的边界[10,11]，并将其运用到三维图像的处理[12]。尽管如此，现有的覆盖分割方法仍有一些不足，比如它们只专注于清晰对象。与此同时，由于其具有更大的收敛范围和自然处理拓扑变化的能力，Chan-Vese模型在图像分割上表现良好[13,14]。然而，它仍然有一些固有的限制，比如分割通常需要依赖于初始轮廓的放置[15]等。

为了解决上述问题，本文提出像素覆盖分割算法和用于边界提取的Chan-Vese模型，首先将图像分割，然后用形态学边缘检测算子检测和连续成像物体边界相交的像素，并用改进的覆盖分割方法重新计算覆盖值，最后用改进的活动轮廓算法提取图像的边界。相对于现有的方法，该方法对具有模糊边界的图像有良好的表现。

1 相关背景

1.1 像素覆盖分割模型

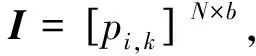
定义一个表示分为m部分的分割矢量Wm，其中所有元素加起来的和为1，即

(1)

把图像I覆盖分割为m部分，可以用一组有序对来表示，即

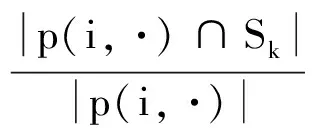
(2)

式中：(i,·)为之前提到的像素位置，α(i)为像素的覆盖值，覆盖值可以近似看作该像素有多少面积和第k类相交。通常情况下，图像第k类的面积值Sk未知，要根据图像数据来估计。

设大小为N的图像可分割为m类，则基于此图像的覆盖分割为A=[αi,j]N×m。其中αi,j为像素i满足约束条件αi,j∈[0,1]的关于物体Sj的覆盖值。矩阵C=[cj,k]m×b为类代表，其中cj,k为第j类在第k个频带上的值。在理想情况下，假定类代表cj,k位置不变，即有

I≈A·C

(3)

但在实际情况下，这种假定会导致覆盖估计的不可信，为了考虑更多的相关估计，允许空间上的不同类代表。比如对于位置x, 有I(x)≈AC(x)。在I≈A·C中，C是公式的基准，要选择最能代表这一类的像素，而不能选择极端的。A为反映I中像素对C归属度的权重。图像分割可以被看作是一个能量最小化的过程，其能量函数可表示为

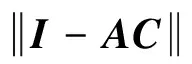
(4)

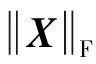
1.2 Chan-Vese模型

经典Chan-Vese(C-V)模型[14]由学者Chan和Vese提出，是一种利用Euler-Lagrange方法求解的简化M-S模型[18]的灰度图像分割方法。然而C-V模型在使用变分水平集方法中的最小化能量泛函实现曲线的演化过程中，仅利用了图像的边缘信息，而忽略了其边界梯度信息。且在能量泛函中添加了面积项Area(inside(C))，与M-S模型中的长度项Length(C)同时控制演化到达被分割物体边界的曲线。设能量泛函为

(5)

式中：I0(x,y)为待分割图像;Length(C)表示边界曲线C的长度;Area(inside(C))为曲线C内部区域的面积;μ,γ≥0;λ1,λ2>0为权重系数。最终，可以通过最优化能量泛函得到分割轮廓线C的位置及未知常量c1,c2。

E{C0,c10,c20}=MinC,c1c2E(C,c1,c2)

(6)

2 基于覆盖分割和活动轮廓模型的图像边缘提取算法

本文提出的边缘提取算法由两步构成，第一步是基于像素覆盖分割算法对图像进行分割，第二步是在分割结果的基础上进行图像边缘的提取。为了克服传统算法的不足，分别对两步算法进行了改进。

2.1 像素覆盖分割模型的改进

针对Sladoje的基于线性分离的像素覆盖分割算法对边界模糊图像的分割效果不理想，且分割结果多毛刺的问题，本文在能量方程中添加一个位置信息项，定义为

(7)

式中：N(Ai,j)为像素i周围8-领域内所有像素点的集合，|N(Ai,j)|为这些像素点的个数。添加位置信息项后，能量方程变为

(8)

式中：λ为位置信息项的权重，经过实验，定为0.05。

要获得一个像素覆盖分割，本文方法由3步构成：(1)利用Sladoje提出的原始像素覆盖分割方法对给定的像素分别分配一个分割向量αi,j，且假设对范围内像素均可提供有效分割；(2)利用多方向模糊形态学边缘检测算法(Multi-directions algorithm for edge detection based on fuzzy mathematical morphology, MDFMED)[19,20]，检测和连续成像物体边界相交的像素。假定这些像素是混合的，且被两个或多个物体覆盖。但在步骤(1)中，每个像素仅被分给一个物体，因此需重新检测并分配覆盖值；(3)采用改进的带有位置信息项的像素覆盖分割方法重新分配混合像素集的覆盖值。

算法1改进的像素覆盖分割算法

输入：待分割图像，分割类数

输出：分割结果

(1)初始化类代表C，隶属度矩阵A;

(2)利用MDFMED选择可能的混合像素集B;

(3)用模糊C均值(Fuzzy C-means,FCM)算法更新矩阵A;

(4)用SPG算法优化矩阵A;

(5)根据矩阵A分割图像。

算法1是改进的像素覆盖分割算法的整体流程图，其中用到了两个经典的优化算法，一个是FCM聚类算法[21]，另一个是上文提到的SPG算法。

2.2 基于Chan-Vese模型的边界提取

在步骤(1)覆盖分割模型中，主要利用色彩信息进行聚类。第2步，本文在原始Chan-Vese模型的基础上，结合测地线活动轮廓(Geodesic active contour,GAC)模型的梯度信息来得到更加准确的分割边界。Chan-Vese模型是基于图像区域的信息，本文使用改进的Chan-Vese模型对步骤1中得到的局部区域信息，进行进一步的细分割，从而获得更好的局部分割结果。

将能量泛函重新定义为

(9)

使用GAC模型中的边缘停止函数g(x,y)来控制活动轮廓曲线演化的长度项和面积项加权，边缘停止函数定义为

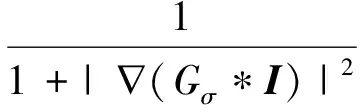
(10)

式中Gσ为高斯核函数。

使用显式欧拉方法数值求解最小化能量泛函E(c1,c2,φ),将变分法运用到能量方程最小化中，得到欧拉-拉格朗日方程为

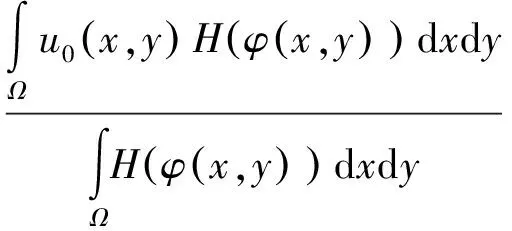
(11)

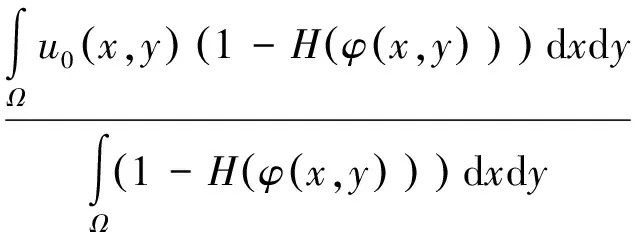
(12)

(13)

最后，使用标准有限差分法对方程进行迭代求解。

算法2改进的Chan-Vese模型。

输入：图像I0(x,y)，差分空间网格步长Δh，迭代时间步长Δt

输出：图像分割实验结果I

(1)初始化相关系数μ,γ,λ1,λ2

(2)WHILE

计算欧拉-拉格朗日方程公式

用梯度下降方法引入迭代时间参数t

更新水平集函数φ

k=k+1

END WHILE

(3)u=uk

3 实验结果与分析

3.1 实验过程

实验在Windows8操作系统下Matlab R2013a进行本文提出的提取边缘的完整算法包括分割和提取两步。第1步基于像素覆盖分割算法，将图像进行分割，第2步将分割结果的边缘用活动轮廓模型提取出来，得到最终实验结果。

图1展示了以USC-SIPI图像库中的一幅风景彩色图像为例的完整的实验过程。图1(a)为实验所用原图，大小为256像素×256像素。用2.1节提出的分割算法将图像分为树、大海、蓝天和陆地3类，分割结果如图1(b)所示。分割后得到了原始图像中的树，再用2.2节提出的边界提取算法提取大树的边缘，最终得到如图1(c)所示的结果。

图1 本文所提的图像边缘提取算法的实验过程展示Fig.1 Experimental procedure of the proposed algorithm for image boundary extraction

3.2 实验评价

为了评价所提算法的性能，将算法运用于美国南加州大学的USC-SIPI图像库、伯克利图像库以及一些经常用于图像分割实验的图像，分别进行分割实验结果的定性比较，分割算法抗噪性测试和提取的边缘对比试验。从中选出分割结果较好的，具有特点的几幅图像，第1幅是Sladoje论文中常用的“辣椒”图像，第2个例子是具有粗糙边界的星云图像，深色背景浅色前景的树叶图像是第3个例子，第4幅是1个人的胎记图像，3.1节提到的彩色风景图像为第5幅。实验结果证实了该方法对边界较模糊的多通道图像的适用性。

3.2.1 覆盖分割实验评价

首先，对待测图像进行覆盖分割实验。将本文提出的改进分割算法与Sladoje 2009年及2012年的两篇论文[8,9]中提出的覆盖分割算法机器改进算法作对比，并将多方向模糊形态学边缘检测算法和Sobel算子以及传统形态学边缘提取算法作对比，结果如图2所示。由图2(a-c)可以看出，分割出的图像边界处有许多毛刺，分割边缘不光滑，图2(c)列图像虽然相比图2(b)列有所改进，但改进并不明显。分别用Sobel边缘检测算子，传统的形态学边缘检测算子和本文算法用到的MDFMED，以发现可能的混合像素集，图2(d-f)列为再分配覆盖值后的结果。可以看出，图像边界越来越平滑，毛刺也越来越少。显然，本文提出的改进算法得到了最好的分割结果，具有最佳性能。

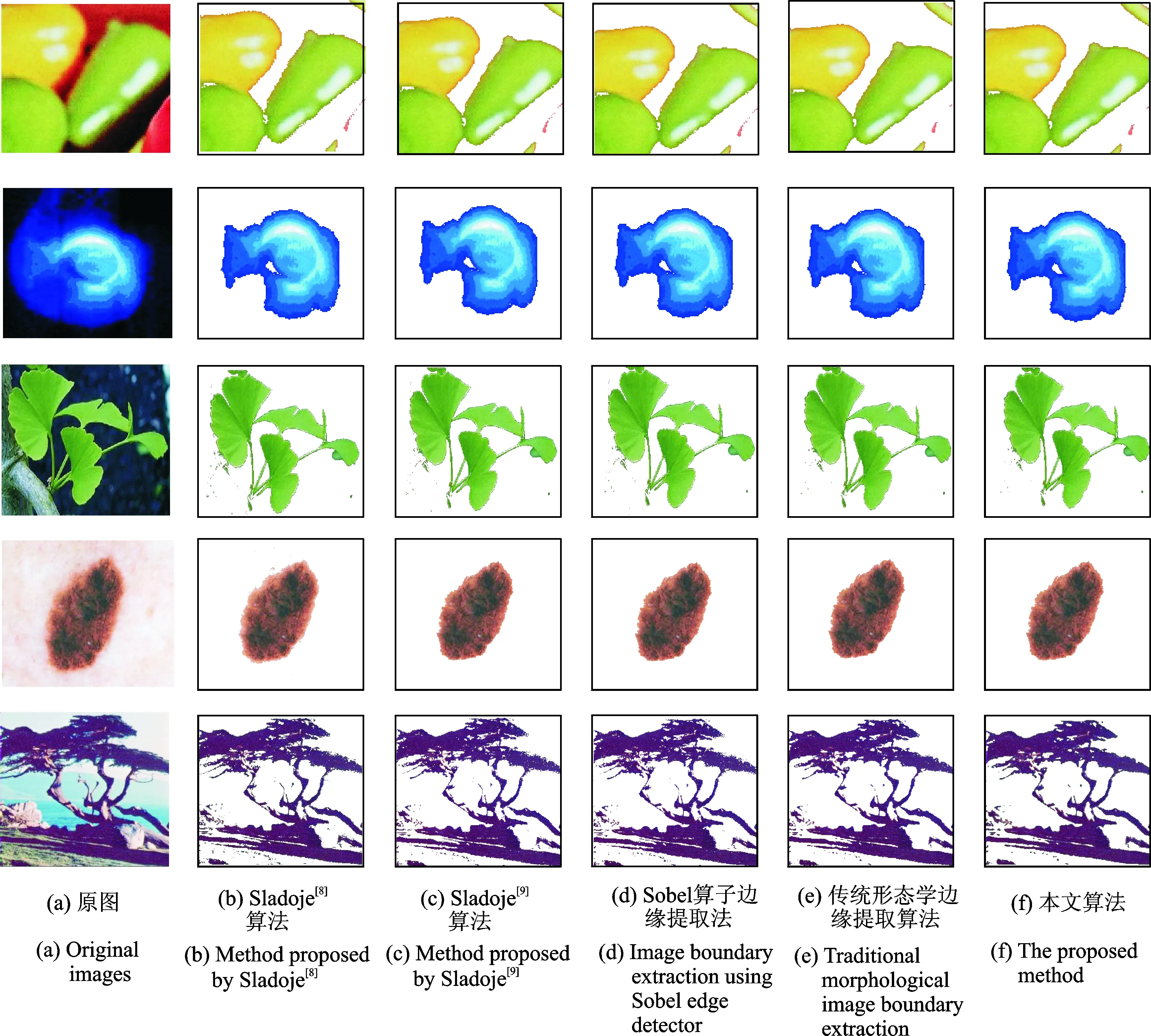
图2 使用不同覆盖分割方法后的图像Fig．2 Comparison of segmenting results using different coverage segmentation methods

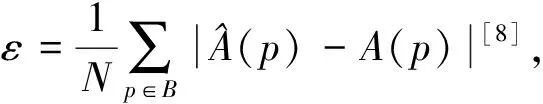
图3显示了当噪声增强时“辣椒”图像的覆盖分割结果，可见图像噪声对结果具有较大的负面影响。本文要探索的，是当噪声增加时各个算法的表现如何。从图3(b)可以看出，加入的高斯噪声越多，改进算法的平均相对误差上升的要比其他算法慢，抗噪性最强。

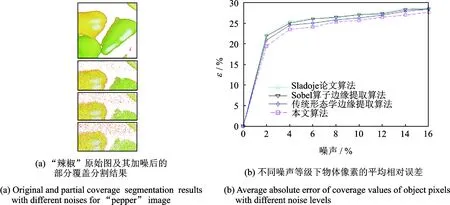
图3 分割算法抗噪性测试结果对比Fig．3 Comparison of robust test results

在对各图像库中的图像进行测试的实验过程中，出现了一些分割效果不理想的情况，图4就展示了两种分割结果不好的情况，第1行为USC-SIPI图像库中的一幅房子图，由于图像边界清晰，前景背景界限明确，本文提出的改进算法与Sladoje论文提出的算法对分割实验结果并没有明显的区别；第2行为伯克利图像库中的袋鼠图，虽然改进算法的分割结果比原始算法有所提高，但由于图像中的干扰因素过多，改进后的算法依然无法将图像主体袋鼠与草地明确的分割开来。这说明本文提出的分割算法在处理边界较模糊、背景不太复杂的图像时更有优势。

3.2.2 边缘提取实验评价

首先将先分割后提取的边界与直接提取的边界作对比；再将改进的分割算法与原始分割算法的分割结果分别进行边缘提取和比较；最后对比改进的Chan-Vese模型与经典Chan-Vese模型在边缘提取结果上的区别,实验结果如图5所示。其中图5(a-c)3列分别为改进的Chan-Vese模型提取原始图像、Sladoje算法分割后的图像和本文改进算法分割后图像的边缘提取结果，图5(d) 列为原始Chan-Vese模型提取本文算法图像边缘的结果。通过图5(a，c)两列的对比可以看出未进行覆盖分割直接提取边界时，由于图像边界较模糊或者背景较复杂，很难得到正确的边界；而改进的覆盖分割算法得到的结果边缘更光滑，所以图5(c)列得到的边缘比图5(b)列要更加圆润连续；从图5(c，d)两列的对比可以看出改进的Chan-Vese模型提高了边界提取的精确度。相比于其他同类算法，因此本文提出的边缘提取算法对具有模糊边界的图像，具有更好的效果。

图4 使用不同覆盖分割方法后出现的不理想的分割结果对比Fig．4 Unsatisfactory segmenting results using different coverage segmentation methods

为了进一步说明本文算法的优势，表1列出了图5(b-d)3列所得到的活动轮廓线的长度。由表可知，在大部分情况下，由本文提出的算法得到的活动轮廓线都是最短的，也就是说，得到的图像边界更光滑，毛刺更少。当然，有时在同样的迭代次数下，原始Chan-Vese模型并不能完成轮廓线的完整提取，因此在表1 中也出现了图5(c)列的数据比图5(d)列要大的情况。

图5 Chan-Vese模型提取经不同算法分割后的图像边缘的结果对比Fig．5 Comparison of different boundary results extracted by Chan-Vese model

3.3 参数实验

在实验过程中，需要确定许多参数。以“辣椒”图为例，用不同的参数分别进行实验，每个参数做一组实验，找出分割效果较好的或活动轮廓线长度较短的，设为实验所用。

图6给出了其中的两组参数设置实验结果，(1)FCM算法中分区矩阵的指数从1.5～2.5以0.1为增长量上升时分别测试提取的活动轮廓线的长度变化结果；(2)位置信息项在能量方程中的权重λ从0.01～0.1以0.01为增长量上升，分别测试提取的活动轮廓线的长度变化结果。从图6(a)可以看出，当指数增长到2.0时，轮廓线长度开始趋于平稳；当指数大于2.0后，虽然轮廓线长度会有少许的减少，但实验所用的时间会大幅增长，所以分区矩阵的指数设为2.0。图6(b)反映λ越大，实验得到的活动轮廓线就会越短，但过大的权重会导致部分不必要的边界平滑，所以λ=0.05是比较理想的选择。

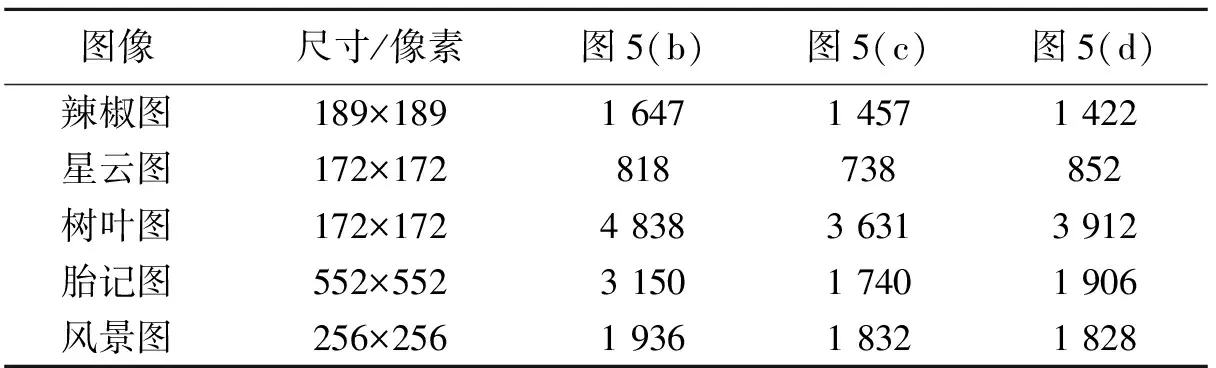
表1 图5实验所得活动轮廓线的长度对比

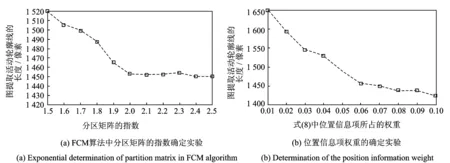
图6 参数设置实验结果Fig．6 Experimental results of parameter setting

4 结束语

本文提出了一种改进的像素覆盖分割算法和Chan-Vese模型相结合的边缘提取算法。用加入了位置信息项的分割算法给物体边界处可能的混合像素集重新分配覆盖值，再用Chan-Vese模型将分割结果的边界提取出来。从实验结果来看加入了位置信息项的像素覆盖分割算法得到的图像边缘更光滑，鲁棒性更好，而改进的Chan-Vese模型也提高了边界提取的精确度。因此，本文提出的方法对于边界模糊的图像，具有更好的边缘提取结果。

[1] 唐利明, 黄大荣, 李可人. 基于变分水平集的图像分割模型[J]. 数据采集与处理, 2014, 29(5): 704-712.

Tang Lim, Huang Darong, Li Keren. New model based on variational level set for image segmentation[J]. Journal of Data Acquisition and Processing, 2014,29(5): 704-712.

[2] 赵胜男, 王文剑. 一种快速均值漂移图像分割算法[J]. 数据采集与处理, 2015, 30(1): 192-201.

Zhao Shengnan, Wang Wenjian. Fast mean shift for image segmentation[J]. Journal of Data Acquisition and Processing, 2015,30(1): 192-201.

[3] Sladoje N, Lindblad J. The coverage model and its use in image processing[J]. Zbornik Radova, 2012, 23: 39-117.

[4] Zhu R, Yao M, Liu Y M. A two-level strategy for segmenting center of interest frompictures[J]. Expert Systems with Applications, 2011, 38(3): 1748-1759.

[5] Sladoje N, Nyström I, Saha P K. Measurements of digitized objects with fuzzy borders in 2D and 3D[J]. Image and Vision Computing, 2005, 23(2): 123-132.

[6] Sladoje N, Lindblad J. High-precision boundary length estimation by utilizing gray-level information[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2009, 31(2): 357-363.

[7] Malmberg F, Lindblad J, Sladoje N, et al. A graph-based framework for sub-pixel image segmentation[J]. Theoretical Computer Science, 2011, 412(15): 1338-1349.

[8] Sladoje N, Lindblad J. Pixel coverage segmentation for improved feature estimation[C]∥International Conference on Image Analysis and Processing. [S.l.]:Springer Berlin Heidelberg, 2009,5716: 929-938.

[9] Lindblad J, Sladoje N. Coverage segmentation based on linear unmixing and minimization of perimeter and boundary thickness[J]. Pattern Recognition Letters, 2012, 33(6):728-738.

[10] Lidayova K, Lindblad J, Sladoje N, et al. Coverage segmentation of thin structures by linear unmixing and local centre of gravity attraction[C]∥8th International Symposium on Image and Signal Processing and Analysis (ISPA) . [S.l.]:IEEE, 2013: 83-88.

[11] Malmberg F, Lindblad J, Nyströ I. Sub-pixel segmentation with the image foresting transform[M]∥Combinatorial image analysis. [S.l.]:Springer Berlin Heidelberg, 2009: 201-211.

[12] Tanács A, Lindblad J, Sladoje N, et al. Estimation of linear deformations of 2D and 3D fuzzy objects[J]. Pattern Recognition, 2015, 48(4):1391-1403.

[13] Wang X F, Huang D S, Xu H. An efficient local Chan-Vese model for image segmentation[J]. Pattern Recognition, 2010, 43(3): 603-618.

[14] Chan T F, Vese L. Active contours without edges[J]. Image processing, IEEE transactions on, 2001, 10(2): 266-277.

[15] Xia R, Liu W, Zhao J, et al. An optimal initialization technique for improving the segmentation performance of Chan-Vese model[C]∥2007 IEEE International Conference on Automation and Logistics. [S.l.]:IEEE, 2007: 411-415.

[16] Birgin E G, Martínez J M, Raydan M. Nonmonotone spectral projected gradient methods on convex sets[J]. SIAM Journal on Optimization, 2000, 10(4): 1196-1211.

[17] Birgin E G, Martínez J M, Raydan M. Algorithm 813: SPG-software for convex-constrained optimization[J]. ACM Transactions on Mathematical Software (TOMS)，2001，27(3): 340-349.

[18] Mumford D, Shah J. Optimal approximations by piecewise smooth functions and associated variational problems[J]. Communications on Pure and Applied Mathematics, 1989, 42(5): 577-685.

[19] Hu D, Tian X. A multi-directions algorithm for edge detection based on fuzzy mathematical morphology[C]∥16th International Conference on Artificial Reality and Telexistence-Workshops.[S.l.]: IEEE, 2006: 361-364.

[20] Zhao Y, Gui W, Chen Z. Edge detection based on multi-structure elements morphology[C]∥The 6th World Congress on Intelligent Control and Automation. [S.l.]: IEEE, 2006, 2: 9795-9798.

[21] Nock R, Nielsen F. On weighting clustering[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2006, 28(8): 1223-1235.

ImageBoundaryExtractionBasedonPixelCoverageSegmentationandChan-VeseModel

Gu Yudi1, Liang Jiuzhen2, Wu Qin2, Li Min2

(1.Network Information & Operation Center, Jiangnan University,Wuxi,214122,China; 2.School of Internet of Things Engineering, Jiangnan University, Wuxi, 214122, China)

Aiming at the problem of unsatisfactory image segmentation effect for images with blurred boundary by using traditional algorithms, a coarse-to-fine approach for image boundary extraction is proposed in this paper, which is made up of pixel coverage segmentation and Chan-Vese model. Based on modified coverage segmentation algorithm and active-contours method, images are firstly segmented by using the original coverage segmentation algorithm and a multi-directions fuzzy morphological boundary detection algorithm is used to extract the boundaries between different objects. Then an improved pixel coverage segmentation method is applied to redistribute coverage values for boundary pixels. Finally, the boundary extraction for refined images is carried out with active-contours algorithm. And qualitative comparison of segmentation results, noise immunity tests and contrast experiments on the extracted boundary are carried out. Experimental results show that the proposed method can obtain more excellent boundary extraction effect than those state-of-the-art methods proposed in comparable literatures.

boundary extraction; coverage segmentation; Chan-Vese model

国家自然科学基金(61170121，61202312)资助项目。

2015-09-24；

2015-11-02

TP391