基于非负矩阵分解的语音深层低维特征提取方法

2017-12-15秦楚雄张连海

数据采集与处理 2017年5期

关键词：语料权值特征提取

秦楚雄张连海

(解放军信息工程大学信息系统工程学院，郑州，450001)

基于非负矩阵分解的语音深层低维特征提取方法

秦楚雄张连海

(解放军信息工程大学信息系统工程学院，郑州，450001)

作为一种基于深层神经网络提取的低维特征，瓶颈特征在连续语音识别中取得了很大的成功。然而训练瓶颈结构的深层神经网络时，瓶颈层的存在会降低网络输出层的帧准确率，进而反过来影响该特征的性能。针对这一问题，本文基于非负矩阵分解算法，提出一种利用不包含瓶颈层的深层神经网络提取低维特征的方法。该方法利用半非负矩阵分解和凸非负矩阵分解算法对隐含层权值矩阵分解得到基矩阵，将其作为新的特征层权值矩阵，然后在该层不设置偏移向量的情况下，通过数据前向传播提取新型特征。实验表明，该特征具有较为稳定的规律，且适用于不同的识别任务和网络结构。当使用训练数据充足的语料进行实验时，该特征表现出同瓶颈特征几乎相同的识别性能；而在低资源环境下，基于该特征识别系统的识别率明显优于深层神经网络混合识别系统和瓶颈特征识别系统。

连续语音识别；深层神经网络；半非负矩阵分解；凸非负矩阵分解；低维特征

引言

在传统的连续语音识别(Continuous speech recognition，CSR)中，利用高斯混合模型(Gaussian mixture models，GMM)和隐马尔科夫模型(Hidden Markov models，HMM)进行声学建模是当前语音识别领域最为经典并且最为成熟的建模技术，它具有速度快、复杂度较低以及识别率良好等优点。随着深度学习技术的飞速发展，深层神经网络(Deep neural network，DNN)受到了广泛的关注，并且在语音识别领域取得了巨大成功[1]。

DNN在语音识别中的应用大致分为两类。一类是使用DNN进行语音的声学建模，即使用DNN替代GMM估计HMM的状态发射概率，构建识别率优于传统GMM-HMM系统的DNN-HMM混合系统[2]；另一类是通过训练DNN来提取语音中更为抽象的高层特征，如瓶颈特征(Bottleneck features，BNF)[3]，这类特征往往具有分布平稳、易于建模等特点，使用这些特征配合传统的GMM-HMM建模，可以取得足以媲美DNN-HMM的效果，甚至在一些情况下更加优异[4]。

由于低维特征更易于声学建模，因此基于DNN提取特征的关键技术在于对隐含层输出特征的降维。传统的方法是通过设置瓶颈(Bottleneck, BN)层实现数据的强制降维。Yu等[5]提出通过在DNN中设置一个节点数很小的隐含层来提取BNF，并且发现当使用三音子绑定状态作训练目标时，该方法所提取的BNF可以有效提升自动语音识别(Automatic speech recognition, ASR)的识别率。但是根据文献[4，5]，该方法最大的问题在于DNN中BN层的存在会增大输出层的帧分类错误率。针对该问题，Gehring等[6]提出使用DNN和自编码结合的方式实现降维并提取BNF；Yan等[7]提出使用主成分分析(Principal component analysis, PCA)对DNN的最后一个隐含层的输出特征进行降维得到新特征；Zhang等[8]提出使用低秩矩阵分解(Low-rank matrix factorization)的方法对DNN分解权值矩阵提取BNF进行建模。实验证明这些方法均得到了同DNN-HMM系统相近的识别率。

本文提出一种基于非负矩阵分解(Non-negative matrix factorization，NMF)的降维方法。NMF是由Lee和Seung在1999年[9]提出的一种矩阵分解方法，使用该算法对图像处理时可以学习到一些很好的局部特征。Ding等[10]引入了两种基于NMF原理且适用于包含正负元素矩阵的分解算法——半非负矩阵分解(Semi-nonnegative matrix factorization，SNMF)和凸非负矩阵分解(Convex-nonnegative matrix factorization，CNMF)。基于NMF的算法对数据具有很好的解释性，在图像检索、信号分离等方面具有很成功的应用。在语音信号处理方面，NMF在语音增强和语音去噪方面有着较为广泛的应用。2008年，Wilson等[11]提出使用基于先验信息的NMF对语音进行去噪处理，并通过实验证明NMF对多种噪声的去除能力强于维纳滤波器；2013年，Mohammadiha[12]提出使用基于时域动态的NMF处理方法对语音进行去噪、增强，实验证明该方法优于传统的语音去噪方法。

本文提出在连续语音识别中利用CNMF和SNMF算法提取基于DNN的低维特征，以提升该类特征的性能。首先训练DNN，然后对DNN某一层的权值矩阵进行矩阵分解，使用分解得到的基矩阵作为新的权值矩阵，从而形成新的特征提取层，且该层不设置偏移量。实验表明，使用CNMF所提取的特征具有比SNMF提取特征更为稳定的规律，两者在训练数据充足的条件下，具有和基于传统方法提取的瓶颈特征几乎相同的识别性能；而基于低资源训练数据进行实验时，两者在训练时间代价提升很小的情况下取得了优于传统瓶颈特征的识别性能，且基于CNMF的瓶颈特征更为出色。

1 基于深层神经网络的声学模型和瓶颈特征提取

DNN对训练数据要求较低，输入特征既可以是多种特征的融合特征，也可以是联合前后帧的长时语音特征。图1给出了DNN在语音识别中的两种典型应用的示意图。当前性能最优的DNN声学模型使用三音子绑定状态(Senones)作为训练目标，构成上下文相关深层神经网络隐马尔科夫模型(Context-dependent deep neural network hidden Markov model，CD-DNN-HMM)[13],其结构如图1(a)所示。隐含层激活函数一般使用Sigmoid函数，假设共有L个隐含层，每一层激活元输出xl的表达式为

xl=σ(Wlxl-1+bl) 1≤l≤L

(1)

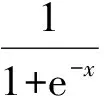
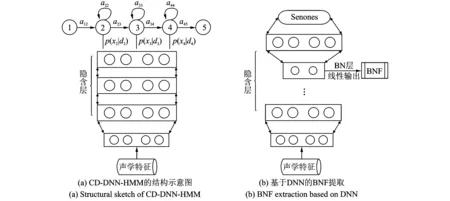
图1 DNN在语音识别中的两种典型应用Fig.1 Two main applications of DNN in speech recognition

在上下文相关(Context-dependent, CD)结构的DNN中，首先需要预先训练三音子GMM模型，然后采取强制对齐的方式得到DNN训练数据的硬性标注，使得输入的每帧声学特征与真实的类别标签信息对应起来。对于Softmax输出层，状态s的后验概率P(s|ot)为

(2)

对DNN直接使用误差反向传播算法(Back propagation，BP)[14]训练易使DNN参数陷入局部最优解，所以往往利用受限玻尔兹曼机(Restricted Boltzmann machine，RBM)对DNN实施逐层预训练以得到更好的初始参数值[15，16]。用v，h分别表示可见层和隐含层，它们之间的能量函数定义为[2]

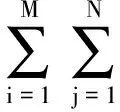
(3)

定义模型关于可见层节点的边缘概率为

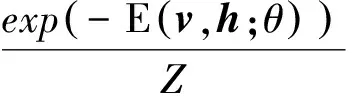
(4)

式中Z为规整因子。通过最大似然准则进行无监督学习，其中训练目标函数为

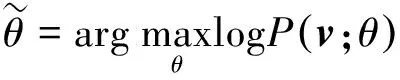
(5)

设Edata(vihj)为实际数据期望值，Emodel(vihj)为重建数据期望值，设RBM预训练时的学习速率为εRBM，目标函数对参数求偏导可得权值的更新式为

Δwij=εRBM(Edata(vihj)-Emodel(vihj))

(6)

预训练之后，采用随机梯度下降(Stochastic gradient descent，SGD)法对训练样本之间的交叉熵(Cross-entropy)代价函数进行优化[13]。设T为样本总量，定义代价函数为

(7)

设ε为学习速率，引入冲量项α和衰减因子η来控制参数更新值的波动，记θ={W,b}统一表示参数，Δθ(i)为第i轮训练参数更新值，则更新过程按式(8)进行修正。

(8)

当使用DNN进行声学建模时，DNN用来估计状态后验概率P(s|ot)，根据贝叶斯准则，按式(9)计算HMM的状态发射概率，然后进行HMM的训练、解码。

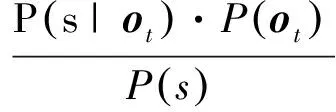
(9)

当使用DNN提取瓶颈特征时，传统的方法是在DNN中设置瓶颈层，如图1(b)所示。用F表述BNF向量，训练完之后，F可表示为

(10)

该特征配合传统的GMM进行建模可以取得较传统声学特征(如梅尔频率倒谱系数(Mel-frequency cepstral coefficients, MFCCs)、感知线性预测(Perceptual linear predictive, PLP)系数等)更好的效果。然而，由于BN层的存在降低了DNN的分类错误率，因此该特征提取方法有待优化。

2 基于非负矩阵分解的低维特征提取

针对第1节引出的问题，本节将通过几种NMF方法对DNN隐含层的线性输出实现降维，以提取性能更优的低维特征，着重介绍基于两种NMF算法的特征提取方法。

2.1 非负矩阵分解

2001年，Lee和Seung在文献[17]中详细介绍了NMF分解算法。该算法针对一个全部为非负元素的矩阵，将其近似分解为一个全部为非负元素的矩阵F和矩阵G，即

X≈FGT

(11)

式中：X为n×m的矩阵，F为n×k的基矩阵，G为k×m的系数矩阵。

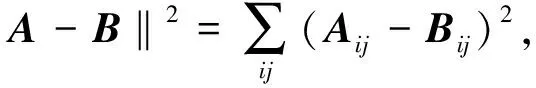
在SNMF和CNMF中，目标依然是找到可以通过相乘逼近待分解矩阵X的矩阵F和G。由于X矩阵中的元素有正有负，因此分解时F矩阵中的元素符号同样有正有负，仅限定G矩阵中元素为非负。

首先介绍SNMF算法。对F和G矩阵初始化之后，采用新的准则对F和G进行更新迭代。

固定G矩阵不变，更新F矩阵为

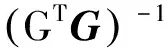
(12)

式中：GTG为一个k×k且元素为正值的半正定矩阵，多数情况下GTG是非奇异的，当GTG奇异时，取其伪逆。

然后固定F矩阵，更新G矩阵为

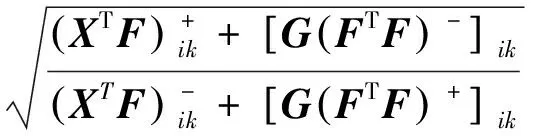
(13)

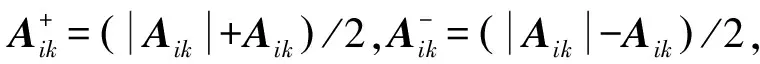
CNMF不同于SNMF。在CNMF中，将基矩阵F定义为待分解矩阵的列的凸组合。即fl=w1lx1+…+wnlxn，或写为F=XW。根据文献[10]，因子矩阵W和系数矩阵G具有稀疏的性质。

CNMF的初始化分为两种方法，一是基于K-means聚类方法，二是基于已有NMF解或SNMF解的初始赋值方法，本文选用K-means方法。首先对待分解矩阵X作一次K-means聚类，得到隶属度矩阵H=(h1,…,hk),Hik={0,1}，基于H对G矩阵初始化，即

G(0)=H+0.2E

(14)

式中E为全1矩阵。使用聚类的类心矩阵作为F矩阵，即

(15)

初始化之后进行迭代运算，更新G的值为

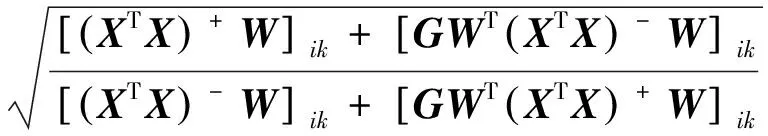
(16)

更新W的值为

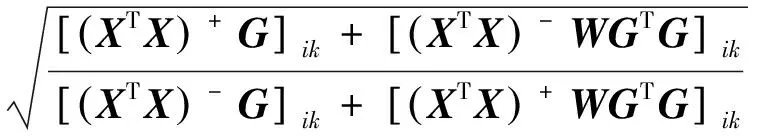
(17)

2.2 基于凸非负矩阵分解和半非负矩阵分解的低维深层特征提取

对于一个不包含BN层的DNN，它的第l隐含层的线性输出具有维数大、相关性大的特点，不适合直接进行GMM的声学建模，因此需要对DNN特征降维。若直接利用矩阵分解算法对DNN特征数据作降维，理论上并不好，其原因是，首先无法针对一帧特征向量做矩阵分解变换；其次，当通过组合多帧特征形成特征矩阵时，矩阵分解会产生结构性的变化，进而破坏语音特征的时序信息，也就无法训练出良好的声学模型。

由于无法直接对隐含层的线性输出作变换，因此本文采用一种间接降维的方法。在计算DNN隐含层的线性特征时，层与层之间的权值矩阵作用于每一帧特征，权值矩阵可以看作是一种广义的映射函数，具有一定的整体分布性。又由于权值矩阵元素有正有负，因此适合于作矩阵分解。而由于同一层的偏移向量和权值矩阵并没有整体联系，因此很难对偏移向量实施与权值矩阵相同的操作。本方法中，对权值矩阵分解的目的在于实现矩阵列的降维，进而实现对特征数据的降维。而低资源数据条件下训练的DNN隐含层权值矩阵具有收敛极不充分的特点，因此该矩阵对特征数据的线性变换效果很有限。针对低资源训练的权值矩阵中存在大量冗余项，可以通过矩阵分解算法从矩阵中提取更基本的分类变换信息。一些常用的矩阵分解方法对于本方法而言具有较大的局限性。首先，特征值分解只能针对方阵，且分解得到的矩阵与原矩阵尺寸相同，因此无法实现降维；其次，奇异值分解将矩阵分解为左奇异分量、奇异值矩阵和右奇异分量，它们都包含了原矩阵中很多的有效信息，无论使用哪一个分量作为新的特征矩阵，浪费的矩阵分量都过多。而对于SNMF和CNMF，根据式(11)，所分解得到的基矩阵包含正负元素，它作为主分量包含了原权值矩阵中的主要分类信息，适合构建新的特征提取层，而系数矩阵作为次分量仅包含非负元素，不具备形成权值矩阵的条件。当然，系数矩阵包含对基矩阵的组合系数，所以一定包含一些有效信息，但是对本文所提出的特征提取过程的贡献不大，所以在此舍弃了系数矩阵的使用。

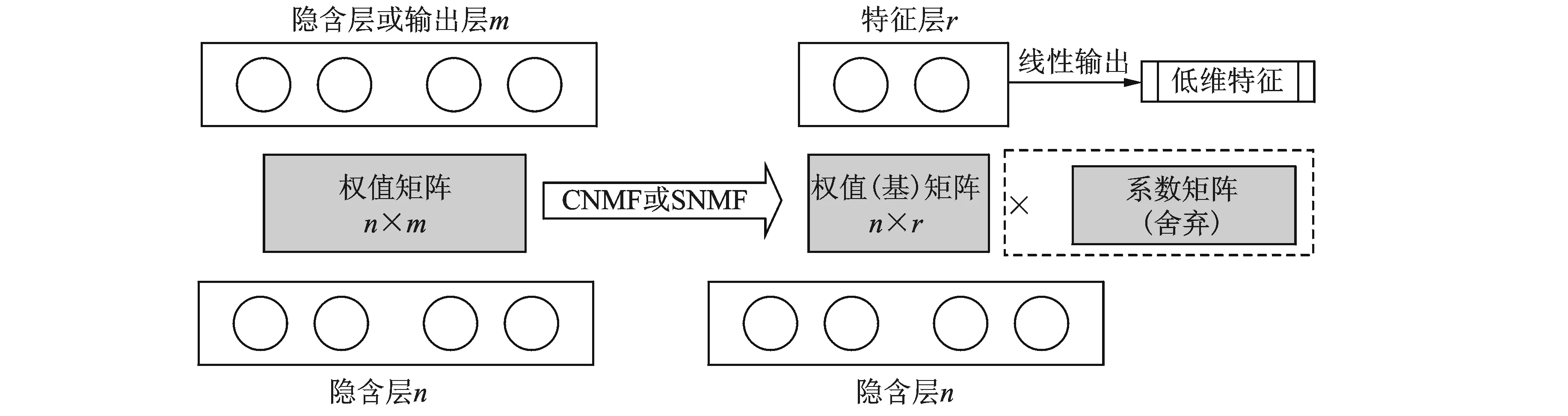
图2 基于SNMF/CNMF的低维特征提取方法Fig.2 SNMF/CNMF based low-dimensional feature extraction approach

综上所述，基于SNMF和CNMF两种算法提取深层低维特征的方法如图2所示。首先对某一层的n×m权值矩阵分解，得到n×r的基矩阵和r×m的系数矩阵，然后使用包含正负元素的基矩阵作为新的权值矩阵，形成新的特征提取层，并提取维数为r的低维特征。设待分解的权值矩阵为W，经过W=W′GT的分解，计算出新特征F′，即

F′ =W′TU

(18)

式中U为上一隐含层的激活元输出，不设置特征层偏移量，因此计算不包含该项。

SNMF和CNMF算法对含有正负元素的矩阵进行分解时往往可以得到更好的数据解释性。它们在算法性能上各有千秋，首先，使用SNMF比使用CNMF的方法得到解的精度更高一些；其次，CNMF可以得到比SNMF更稀疏的解；最后，CNMF的解比SNMF的解具有更好的正交性。进一步进行推导，在CNMF中，设H为因子矩阵(因子矩阵在2.1中用W表示，这里为了与权值矩阵区分，用H表示)，则有W=W′H，因此式(18)可写为

F′=HTWTU

(19)

可知，基于CNMF的方法相当于对权值矩阵作了一次列的线性变换，比基于SNMF的方法更符合权值矩阵降维的实际要求，又因为它的初始化是基于K-means聚类而不是随机初始化，因此CNMF低维特征理应具有更稳定的性能。

3 实验部分

3.1 实验语料

采用训练数据充足的语料和训练数据不足的低资源语料两种语料进行实验，分别测试本文所提出的特征在两种环境下的识别性能表现。一是RM语料，RM语料库是由美国国防部高级研究项目局(Defense advanced research projects agency，DARPA)牵头收集定制的较为早期的英语语料库，语料经过数字采样和文本标注，专门用于设计和评估连续语音识别系统。RM语料模拟训练语料较为充足的情况。二是Vystadial 2013 Czech data(Vystadial_cz)，它是开源的捷克语语料库，全部时长15 h，来源于3类数据：Call Friend电话服务的语音数据、Repeat After Me的语音数据和Public Transport Info的口语对话系统的语音数据。实验随机选取Vystadial_cz语料库中约1 h(1.06 h)的训练语音文件组成训练集，以模拟低资源的条件；再选取语料库中约30 min的测试语音数据作为测试集，测试集包含666句话，共3 910个待识别词；使用Vystadial_cz语料库中全部训练语料的标注文本训练语音识别系统的二元语言模型。

3.2 实验工具与评价指标

实验使用Kaldi工具包[18]进行数据准备、底层声学特征和高层声学特征的提取、语言模型的声学模型的训练与解码；使用PDNN工具包[19]基于GPU(Quadro 600)进行相关的DNN的搭建与训练；使用PYMF工具包[20]实现SNMF和CNMF等分解算法。

实验评价指标采用连续语音识别中的词错误率(Word error rate，WER)，设N为语料库人工标注文本中词(全部正确词)的数量，W为解码连续语音与人工标注作对比统计出的插入词、删除词和替代词的个数，r表示WER，将WER定义为两者的比值，并化为百分率，即

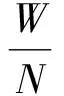
(20)

3.3 基线系统

首先对于RM语料，基于13维的MFCC特征，训练一个基于线性判别分析(Linear discriminant analysis，LDA)(9帧拼接，LDA降到40维)、最大似然线性变换(Maximum likelihood linear transform，MLLT)和说话人自适应训练(Speaker adaption training，SAT)且高斯混元数为9 000的三音子GMM声学模型。根据该模型提取40维的特征空间最大似然线性回归(feature-space Maximum likelihood linear regression，fMLLR)特征，再通过前后5帧的拼接得到DNN的输入特征，这样一来DNN的输入层节点数为440个。之后使用该模型中的senones强制对齐得到DNN的硬性标注，实验中DNN的Softmax层一共有1 487个节点。基于RM语料设置两个提供对比的基线系统。第一个是基于CD-DNN-HMM的识别系统，其DNN结构设置为“440-1 024-1 024-1 024-1 024-1 024-1 024-1 487”；第二个是基于BNF训练的子空间高斯混合模型(Subspace Gaussian mixture models，SGMM)的识别系统。经多次实验表明，BN-DNN设置为“440-1 024-1 024-1 024-1 024-40-1 024-1 487”时BNF的性能最佳，该系统声学模型为基于LDA(9帧拼接后降至40维)、MLLT且高斯混元数为9 000的三音子GMM，经过强制对齐后，训练高斯混元数为400的通用背景模型(Universal background model，UBM)，然后训练子状态数为9 500的SGMM。

对于Vystadial_cz的低资源语料，其训练过程类似于RM识别系统。首先基于13维的MFCC特征训练一个基于LDA(9帧拼接，降至40维)，MLLT和SAT且高斯混元数为22 000的三音子GMM，同样基于此模型提取40维的fMLLR特征，将其进行11帧拼接，作为DNN的输入。Vystadial_cz的基线系统同样为CD-DNN-HMM和BNF-SGMM。对于CD-DNN-HMM，DNN的结构设置为“440-1 024-1 024-1 024-1 024-1 024-915”；对于BNF-SGMM系统，同样经实验验证DNN设置为“440-1 024-1 024-1 024-40-1 024-915”时最佳，然后提取BNF训练基于LDA(9帧拼接后降至40维)，MLLT且高斯混元数为22 000的三音子GMM，经过强制对齐后，训练高斯混元数为400的UBM，并训练子状态数为5 000的SGMM。

所有DNN的训练参数设置均相同。设置学习速率初始值为0.08，每当相邻两轮训练的验证误差小于0.2%时，就将学习速率衰减一半，当衰减之后相邻两轮的验证误差再次小于0.2%时训练停止(如果一直大于0.2%，则最多衰减8次)；冲量值设为0.5；minibatch尺寸设为256。

3.4 对比实验

基于基线系统的DNN模型，对DNN的权值矩阵做CNMF和SNMF。根据第2节中的算法，通过50轮K-means聚类方法对CNMF进行初始化，通过随机赋值的方法对SNMF进行初始化。两种方法都作500次迭代训练从而实现分解。将该低维特征简记为其英文缩写LDF(Low-dimensional feature)，则实验中的两种特征分别记为CNMF-LDF和SNMF-LDF。

使用新的特征训练SGMM声学模型并解码，其训练过程、参数设置与基线系统相同。对于分解过程来说，针对DNN的哪一层进行分解、分解维数为多少，这两个变量因素都会影响所提取特征的性能。设第1个隐含层与第2个隐含层之间的权值矩阵所在位置称为第1层，对于RM语料的DNN而言，第6个隐含层与输出层间的权值矩阵所在位置为第6层，共6个待分解位置；对于Vystadial_cz语料的DNN而言，共5个待分解的位置。由于较高层的输出特征明显优于较低层的特征，因此本实验针对后3个待分解位置进行对比；此外，根据经验，实验主要针对分解维数为30，35，40，45，50的情况进行研究。对这两个变量研究的实验结果分别如图3，4所示。

从图3(a，b)中可知，使用SNMF时，对最后一层分解40维、对倒数第二层分解30维、对倒数第3层分解50维时效果相对更好，但是最好的分解位置和维数并不随网络结构的变化而具有固定的规律；由图4(a，b)可知，使用CNMF时，对每一层普遍进行40维分解时效果更好，且对倒数第2层权值矩阵分解40维时可以取得最好的效果。总体来说，CNMF-LDF比SNMF-LDF具有更稳定的建模规律，其主要原因在于CNMF通过50轮的K-means聚类进行初始化而SNMF通过随机赋值进行初始化。而在40维左右时取得最好的性能这一结果，说明CNMF起到了与传统方法中BN层相类似的作用，即对输入特征实现了非线性压缩。至于在倒数第2层取得最优性能这一结果，说明该特征和BNF有类似的结论，都是将特征层置于DNN中间靠后的隐含层时效果最佳。

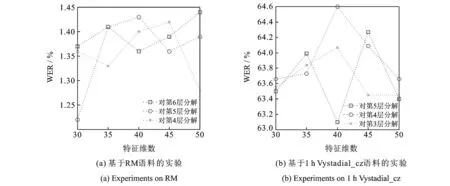
图3 不同分解位置和维数对SNMF特征的影响Fig.3 Effects of different factorization locations and dimensions on SNMF

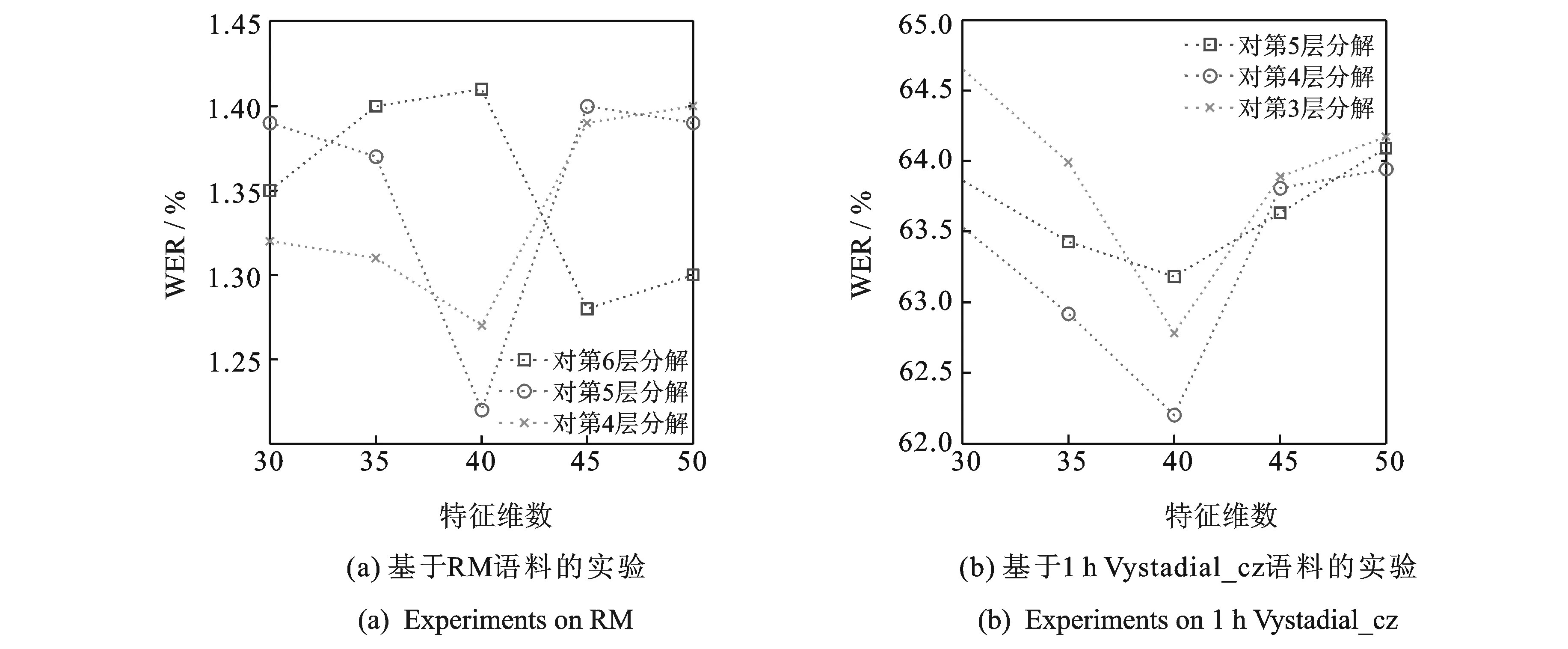
图4 不同分解位置和维数对CNMF特征的影响Fig.4 Effects of different factorization locations and dimensions on CNMF

基于前文对参数的研究，实验选取SNMF与CNMF中的最优结果与基线系统进行对比，结果如表1所示。

表1 在RM语料下不同系统的对比结果

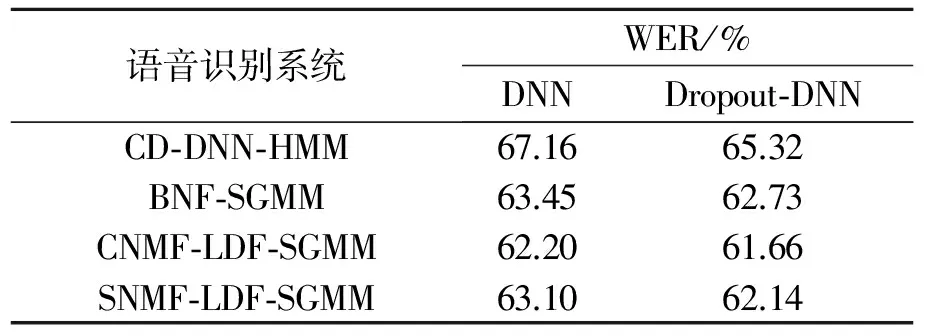
表2 基于dropout训练的不同低资源识别系统的对比结果

由表1结果可知，在训练语料较为充足的RM实验中，CNMF-LDF与SNMF-LDF可以在建模时取得相同的识别率，但两者的性能与传统方法所提取的特征几乎相同。

而文献[21]表明，引入dropout训练技术可有效提高低资源下的DNN训练效果。在此基于前一实验设置，对DNN的隐含层引入dropout进行训练，以进一步验证该方法对于DNN的有效性。实验中，保持DNN的其他训练参数设置和不引入dropout时一致，仅仅在每一轮的训练中，对每个隐含层引入遗弃因子(Hidden drop factor，HDF)，根据文献[21]的经验，将该值设置为0.2，即每一轮训练中，每一个隐含层都有约20%的节点参数不参与本次更新。各系统的实验结果如表2所示。由表2可知，在训练语料不足的条件下，两种特征均优于传统的BNF，且CNMF-LDF的识别性能更突出一些，它相对CD-DNN-HMM提高了7.4%(67.16%→62.20%)，相对基线BNF-SGMM提高了2.0%(63.45%→62.20%)。当引入dropout技术提升DNN性能时，仍然得到了类似的对比结果，SNMF-LDF和CNMF-LDF依然优于BNF的识别性能，且基于CNMF-LDF的识别系统依然取得了最好的识别率，分别相对基线CD-DNN-HMM和BNF-SGMM提高了5.6%(65.32%→61.66%)和1.7%(62.73→61.66%)。基于以上实验结果，本文认为使用CNMF提取特征为更优的方法。

分析认为，权值矩阵训练充分与否直接影响了对输入特征的变换能力的好坏。当训练数据充足时，传统方法中BN层的权值矩阵收敛充分，因此BN层对输入数据可以进行充分的非线性变换，从而提取性能出色的BNF，此时使用基于NMF的方法体现不出优越性；当训练数据不足时，DNN的权值矩阵训练不足，BN层对输入特征的变换不充分，而此时使用NMF算法可以从高维权值矩阵提取出更为本质的低维矩阵，相当于对权值矩阵实施了进一步的训练，因此该方法体现出了比传统方法更优越的性能，尤其当使用聚类性能更好的凸非负矩阵分解时，其基矩阵具有更好的稀疏特性和更好的变换效果，因此所提取的特征性能更出色。而在低资源下，SNMF-LDF、CNMF-LDF基于DNN和Dropout-DNN都取得了最好的识别结果，也说明了本文方法对于低资源数据条件下多种结构DNN的适用性。

通过实验验证，本文所提出低维特征与BNF在模型训练和解码时所用时间基本相同，主要的时间代价差别存在于特征提取过程。虽然从网络参数规模的角度来说，设置BN层的DNN参数比不设置BN层的DNN参数更少一些，但在训练数据量很小的低资源情况下，两者在训练时间上几乎没有差别(尤其是使用高性能GPU时)，加之非负矩阵分解的迭代训练速度很快，因此该方法和设置BN层的方法在训练时间代价上相差无几。本文所提出的方案以微小的时间代价换取了可观的识别性能提升。

4 结束语

在连续语音识别中利用瓶颈特征进行高斯混元建模的过程中，针对DNN提取瓶颈特征时，设置BN层会影响DNN的训练效果这一问题，本文提出一种新的利用DNN提取特征的方法。使用已训练好的DNN模型，基于CNMF和SNMF算法对隐含层权值矩阵做分解，将得到的基矩阵作为新的特征提取层的权值矩阵，在不设置偏移量的前提下，提取新的低维特征。实验表明，CNMF的方法比SNMF的方法具有更为稳定的规律，两种方法在训练数据充足的情况下，取得了同基线系统相同的性能；而在权值矩阵得不到充分训练的低资源语料环境下，这两种方法均以极小的时间代价换取了相对传统方法的识别率的提升，且CNMF的效果更为明显。

[1] Hinton G E, Deng L, Yu D, et al. Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups[J]. IEEE Signal Process Mag, 2012,29(6):82-97.

[2] 戴礼荣，张仕良.深度语音信号与信息处理：研究进展与展望[J].数据采集与处理，2014，29(2)：171-179.

Dai Lirong, Zhang Shiliang. Deep speech signal and information processing: Research progress and project[J]. Journal of Data Acquisition and Processing, 2014, 29(2): 171-179.

[3] Grézl F, Karaat M, Kontar S, et al. Probabilistic and bottle-neck features for LVCSR of meetings [C]//IEEE International Conference on Acoustics, Speech and Signal Processing. Honolulu, HI: IEEE, 2007: 757-760.

[4] Bao Yebo, Jiang Hui, Dai Lirong, et al. Incoherent training of deep neural networks to de-correlate bottleneck features for speech recognition [C]// IEEE International Conference on Acoustics, Speech and Signal Processing. Vancouver, BC: IEEE, 2013: 6980-6984.

[5] Yu D, Seltzer M L. Improved bottleneck features using pretrained deep neural networks[C]//Proc Interspeech. Florence, Italy: International Speech Communication Association, 2011: 237-240.

[6] Gehring J, Miao Y J, Metze F, et al. Extracting deep bottleneck features using stacked auto-encoders [C]//IEEE International Conference on Acoustics, Speech and Signal Processing. Vancouver, BC: IEEE, 2013: 3377-3381.

[7] Yan Z J, Huo Q, Xu J. A scalable approach to using DNN-derived features in GMM-HMM based acoustic modeling for LVCSR [C]//In Proc INTERSPEECH. Lyon, France: International Speech Communication Association, 2013: 104-108.

[8] Zhang Y, Chuangsuwanich E, Glass J R. Extracting deep neural network bottleneck features using low-rank matrix factorization [C]// IEEE International Conference on Acoustics, Speech and Signal Processing. Florence, Italy: IEEE, 2014: 185-189.

[9] Lee D D, Seung H S. Learning the parts of objects by non-negative matrix factorization [J]. Nature，1999，401(6755): 788-791.

[10] Ding C, Li T, Jordan M I. Convex and semi-nonnegative matrix factorizations[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(1): 45-55.

[11] Wilson K W, Raj B, Smaragdis P, et al. Speech denoising using nonnegative matrix factorization with priors[C]// IEEE International Conference on Acoustics, Speech and Signal Processing. Las Vegas, USA: IEEE, 2008: 4029-4032.

[12] Mohammadiha N. Speech enhancement using nonnegative matrix factorization and hidden markov models[D]. Stockholm: KTH Royal Institute of Technology, 2013.

[13] Dahl G E, Yu D, Deng L, et al. Context-dependent pre-trained deep neural networks for large vocabulary speech recognition[J]. IEEE Transactions on Audio, Speech and Language Processing, 2012, 20(1):30-42.

[14] Rumelhart D E, Hinton G E, William R J. Learning representations by back-propagating errors[J]. Cognitive Modeling, 2002, 1: 213.

[15] Hinton G E, Osindero S, Teh Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006,18(7):1527-1554.

[16] Mohamed A, Dahl G E, Hinton G. Acoustic modeling using deep belief networks [J]. IEEE Transactions on Audio, Speech, and Language Processing, 2012,20(1):14-22.

[17] Lee D D, Seung H S. Algorithms for non-negative matrix factorization[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2000:556-562.

[18] Povey D, Ghoshal A, Boulianne G, et al. The Kaldi speech recognition toolkit [C]// IEEE Workshop on Automatic Speech Recognition and Understanding (ASRU). Waikoloa, Hawaii, USA: IEEE, 2011:1-4.

[19] Miao Y J. Kaldi+PDNN: Building DNN-based ASR systems with Kaldi and PDNN [J]. Eprint Arxiv, 2014: 1401.6984.

[20] Thurau C. Python matrix factorization module[EB/OL]. https://pypi.python.org/pypi/PyMF/0.1.9, 2011-04-28.

[21] Miao Y J, Metze F. Improving low-resource CD-DNN-HMM using dropout and multilingual DNN training [C]//Proc Interspeech. Lyon, France: International Speech Communication Association, 2013: 2237-2241.

NonnegativeMatrixFactorizationBasedDeepLow-DimensionalFeatureExtractionApproachforSpeechRecognition

Qin Chuxiong, Zhang Lianhai

(Institute of Information System Engineering, PLA Information Engineering University, Zhengzhou, 450001, China)

As a type of deep neural network (DNN) based low-dimensional feature, bottleneck feature (BNF) has achieved great success in continuous speech recognition. However, the existing of bottleneck layer reduces the frame accuracy of output layer when training a bottleneck deep neural network (BN-DNN), which in return has a bad impact on the performance of bottleneck feature. To solve this problem, a nonnegative matrix factorization based low-dimensional feature extraction approach using DNN without bottleneck layer is proposed in this paper. Specifically, semi-nonnegative matrix factorization and convex-nonnegative matrix factorization algorithms are applied to hidden-layer weights matrix to obtain a basis matrix as the new feature-layer weights matrix, and a new type of feature is extracted by forward passing input data without setting a bias vector in the new feature-layer. Experiments show that the feature has a relatively stable pattern around different tasks and network structures. For corpus with enough training data, the proposed features have almost the same recognition performance with conventional bottleneck feature. Under low-resource environment, the recognition accuracy of the new feature-tandem system outperforms both DNN hybrid system and bottleneck-tandem system obviously.

continuous speech recognition; deep neural network; semi-nonnegative matrix factorization; convex-nonnegative matrix factorization; low-dimensional features

国家自然科学基金(61175017，61403415)资助项目。

2015-07-30；

2016-02-21

TN912.34