系统LT码在删除信道下的渐进性能分析及度分布设计

2017-12-15徐大专许生凯

数据采集与处理 2017年5期

关键词：渐进性译码误码率

华洁徐大专许生凯

(1．南京航空航天大学江苏省物联网和控制技术重点实验室，南京，211106；2.南京航空航天大学电子信息工程学院，南京,211106)

系统LT码在删除信道下的渐进性能分析及度分布设计

华洁1，2徐大专1，2许生凯1，2

(1．南京航空航天大学江苏省物联网和控制技术重点实验室，南京，211106；2.南京航空航天大学电子信息工程学院，南京,211106)

首先基于与或树分析法，对系统LT码在删除信道下的渐进性能公式进行推导，并给出其下限。仿真结果表明当开销足够大时，实际误码率，渐进性能与下限三者完美匹配。然后根据渐进性能，提出改进的优化模型(Improved systematic linear programming,ISLP)对度分布进行优化设计。优化所得的度分布明显优于鲁棒孤波分布(Robust soliton distribution,RSD)分布与截断度分布(Truncated degree distribution,TDD)分布。另外，优化后的度分布其渐进性能可由设定的开销与误码率进行控制，即在所设置的开销之内达到理想的误码率，这一特性可进一步影响完全译码时所需开销。仿真结果表明，数据恢复时所需的开销与所设置的开销相近。对比系统LT码和LT码的误码率与恢复原始数据时所需的开销和编译码时间，表明系统LT码能比LT码更快地恢复原始数据，具有更优的性能。

渐进性能；度分布；线性优化；系统LT码

引言

二进制删除信道(Binary erasure channel,BEC)是典型的删除信道模型[1]。在网络传输过程中，数据要么被正确接收要么被丢弃，因此，因特网的传输表现出明显的删除信道特征。为解决数据在传输中的丢包问题，回复重传技术(Automatic repeat request,ARQ)应运而生。但随着用户需求的增加，ARQ所引发的 “反馈风暴”也大幅度降低了网络传输效率。针对这一问题，Luby提出了数字喷泉码的概念，但并未构造出实用的数字喷泉码[2-5]。2002年，Luby[6]设计LT码作为第一种实用的数字喷泉码，并为其设计度分布——鲁棒孤波分布(Robust soliton distribution, RSD)，使其能在任意删除信道中逼近信道容量。

非系统是LT码的缺点之一，而系统LT码在完成LT编码符号之前发送输入符号。从文献[7]已知，系统LT码优于非系统码。因此，本文在删除信道下针对系统LT码进行分析与度分布设计。Nguyen等[7,8]对系统LT(Systematic Luby transform, SLT)码进行定义并给出了一种截断度分布(Truncated degree distribution, TDD)，该度分布能使系统LT码具有与RSD分布相近的性能。然而，TDD分布仍不是最优分布。经过对传统系统LT码结构的修改，文献[9]提出了一种新的无码率码，消除了LT码原有的错误平底现象。文献[10]中介绍了一种复杂度更低的LT码——准系统参杂LT(Quasi-systematic doped LT, QS-DLT)码。为提高效率，在高斯信道下，文献[11]通过改变LT码的编码方式，使得输入度分布不再服从泊松分布。文献[8]则通过分析系统LT码的译码特性并对RSD分布进行修改而得到TDD分布。

综上，现有的SLT码的研究，有的通过改变编码方式提高系统LT码性能；有的基于对系统LT的译码概率分析设计度分布；有的在原有度分布的基础上进行修改，得到新的度分布。而本文将对系统LT码的渐进性能进行分析，并以此为依据设计度分布，主要的工作包括：(1) 对系统LT在删除信道下的性能进行分析。通过与或树分析方法对系统LT码的渐进性能进行推导，并给出明确的表达式，同时获取渐进性能的下限。理论数据与仿真结果相符合，推导成立；(2) 基于渐进性能与其下限，设计优化模型，并对系统LT码的度分布进行优化。结果表明，优化所得的度分布性能优于RSD和TDD。另外，在设置的开销内，可达到理想的误码率。这表明，可以控制度分布的误码率性能并进一步影响恢复数据时的开销。仿真结果表明，成功译码时的开销与所设置的值相近；(3) 在不同删除概率下，对系统LT码与LT码进行比较。结果表明，删除信道下系统LT码在恢复数据上所花费的编译码时间小于LT码，显示了在快速恢复数据方面优于LT码的性能。

1 系统LT码

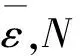
当系统LT在删除信道下传输时，删除概率p是一个非常重要的参数。当信道条件良好，即p非常小时，可以通过系统部分的码字对原始信息进行恢复，这大大降低了对度分布设计的必要性，所以本文主要对具有高删除概率(p≥0.5)的信道进行讨论。

2 渐进性能

Luby使用“与或树”对LT码的译码过程进行分析。

假设Tl为深度为2l的树，深度为0,2,…,2l的节点为或节点，对其子节点进行逻辑“或”运算；深度为1,3,…,2l-1的节点为与节点，对其子节点进行逻辑“与”运算。或节点有i个子节点的概率记为δi,i∈{1,2,…,O}，与节点有j个子节点的概率记为βj,j∈{1,2,…,A}，{δ1,δ2,…,δO}和{β1,β2,…,βA}均为概率分布。树中的每一个节点被记为0或者1。0表示该节点未被恢复1则相反。假设a表示或节点为0的概率，b表示与节点为1的概率，则有如下定理[12]。

定理1与或树Tl的根节点为0的概率yl=f(yl-1)，其中yl-1表示树Tl-1的根节点为0的概率

f(x)=a·δ(1-b·β(1-x))

(1)

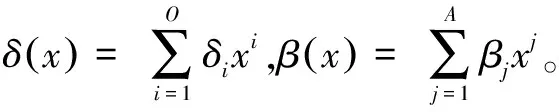
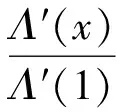
定理2在经过l次迭代后，系统LT的恢复概率为

(2)

定理3在删除概率为p的删除信道下，β为度分布的平均度数，则有

(3)

证明：在第l次迭代中，当l→∞，y=yl=yl-1由于yl-1略大于0，且Ω′(1)=β，则有

并对式(3)进行变形有

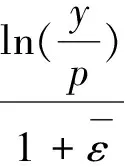
(4)

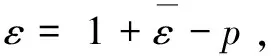
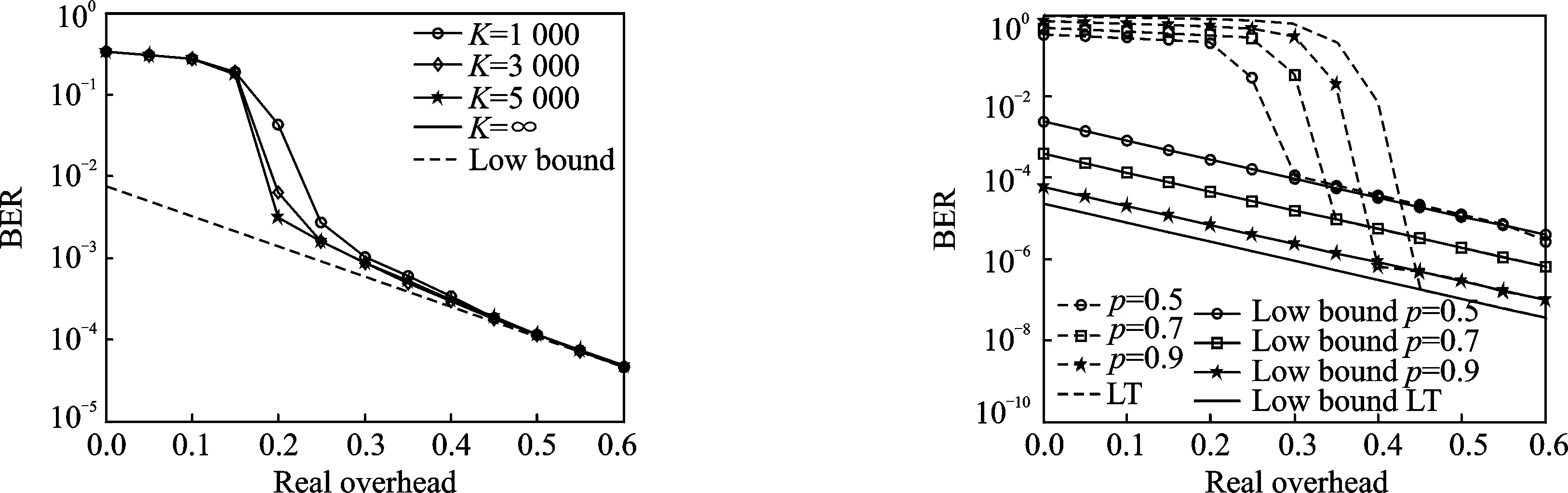
图1 不同码长的系统LT码的误码率图2 在不同删除概率下系统LT码与LT码的误码率
Fig.1 BER performances of different lengths of SLT Fig.2 BER performances of SLT and LT under different erasure probabilities

表1 系统LT与LT恢复数据时所需的平均开销与编译码时间

3 优化模型

本文对度分布的优化模型进行设计，以实现：(1) 编码和译码的复杂度都与Tanner图中的边数呈线性关系，因此控制度分布的平均度数能有效降低编译码的复杂度[12]；(2) 当误码率为y，码长为K时，恢复数据的概率Ps=(1-y)K，为了在理想开销时完成数据的恢复(Ps→1),就必须保证在所设置的开销前，y值足够小。

基于以上两点，将模型LPA[13]向系统LT码进行推广，并对其进行改进。已知，在每一次译码迭代中，都要保证译码过程的方向正确，即yl+1≤yl.，且根据概率分布中每一元素的非负性与和为一的特性，提出系统码的线性优化模型(Systematic linear programming,SLP)，模型如式(5)所示。由第3节所得的渐进性能与其下限，将式(4)作为新的约束对SLP进行改进，得到的模型ISLP由式(6)所示。

(5)

(6)

式中：1-p=x10.5；dmax为度分布的最大度数。

4 仿真结果与分析

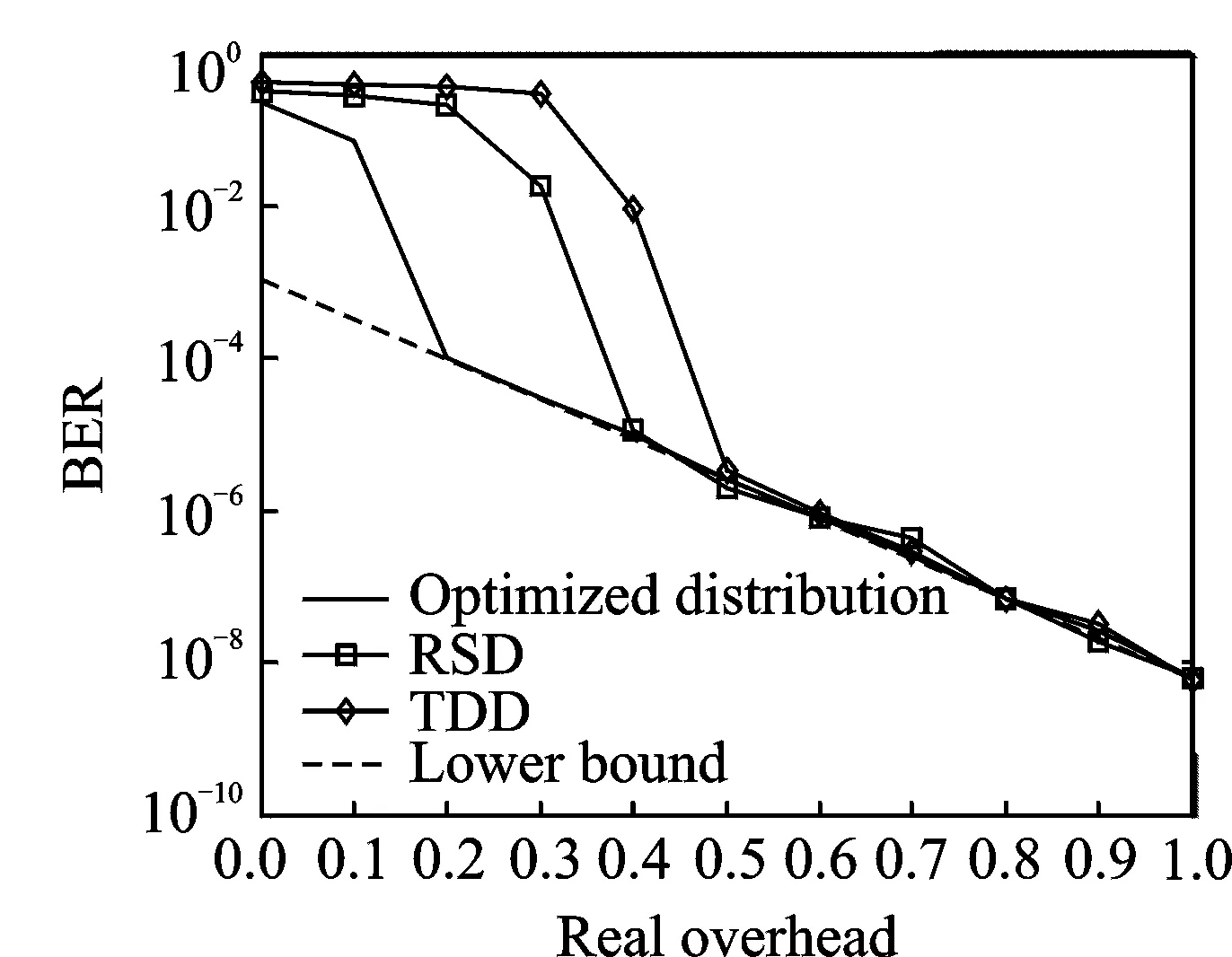
图3 3种度分布下系统LT码的误码率 Fig.3 BER performance of SLT with three degree distributions

为验证优化模型ISLP优化所得的度分布能提高系统LT码的性能，将优化所得的度分布Ω1(x)与经典的RSD和TDD进行对比。3种分布的各项参数如表2所示，原始码长K=3 000，删除概率p=0.5。图3给出了3种度分布的误码率曲线。使用3种度分布时，系统LT码完全恢复数据时所需的平均开销结果如表3所示。由图3所示，虽然当3种度分布有相近的平均度数时，三者的渐进性能下限也相近，但在“瀑布区”，Ω1(x)比另两种度分布下降得更快，最先到达平底，且由表3可知，Ω1(x)恢复数据所需的开销也最小。结合图3与表3，可知当几种度分布有相近的渐进性能下限时，最先下降到此下限的度分布完成原始数据恢复所需的开销最小。

表2 3种度分布各项参数

表33种度分布恢复数据时的开销

Tab.3Overheadstorestoredataofthreedistributions

Ω1x()RSDTDD0．15030．30090．3100

上述仿真表明，使用ISLP优化所得的度分布优于RSD与TDD。现在，对SLP与ISLP进行对比，以验证ISLD中所增加的新约束大大地提高了优化效果。两种模型的参数设置为dmax=100,p=0.8,y=10-4，另外SLP中δ=10-4，ISLP中δ=10-3。比较结果如图4所示。从图4可清楚地看到， ISLP的优化效果明显优于SLP。观察图4中所标出的3个点，在SLP中，只能对点A进行控制，但在ISLP中由于新约束的作用，可以控制点B与点C。点B表明在所希望的开销前，即能达到渐进性能的平底处，点C则表明在所设置的开销时可取得理想的误码率。与点A相比，点B与点C对恢复数据的概率更具影响意义，从而可以进一步对恢复数据的开销进行控制。表4给出了模型ISLP优化度分布恢复数据的开销，可知实现数据恢复的实际开销与所设置的开销相近，这表明模型ISLP对恢复数据所需的开销有一定的控制作用。

图4 模型ISLP与SLP优化度分布的误码率Fig.4 BER of the distributions optimized by ISLP and SLP

ε数值设置0．20．40．6实际0．19820．40970．6106

5 结束语

在删除信道下，由于系统部分码字的作用，系统LT码可以比LT码更快地恢复数据。本文主要在大删除概率的删除信道下针对系统LT码进行了详细研究。通过与或树分析得到系统LT码在删除信道下的渐进性能并得到其下限，且相应的仿真也证明所推得的理论LT码渐进性能与实际性能相符。基于以上结论，本文设计了系统LT码的度分布优化模型，此模型优化所得的度分布有效地提高了系统LT码的误码率性能。仿真结果表明，相比于传统的RSD与TDD，优化所得的度分布能更快地恢复源数据。模型SLP与ISLP的对比结果表明，新添加的约束可以有效地提高度分布的性能，且在使用ISLP模型优化度分布时，系统LT码的误码率性能与恢复数据时所需的开销是可控的。

[1] Elias P, Elias P. Coding for two noisy channels[C]∥ The 3rd London Symposium in Information Theory. London:[s.n.], 1956:61-76.

[2] Byers J W, Luby M, Mitzenmacher M, et al. A digital fountain approach to reliable distribution of bulk data [C]∥Proceedings of the ACM SIGCOMM Conference on Applications, Technologies Architectures, and Protocols of Computer Communication. Vancouver, Canada:ACM,1998,28(4):56-67.

[3] MacKay J C. Fountain codes [J]. IEE Proc Comm, 2005,152(6):1062-1068.

[4] 黄晓可, 刘洛琨, 郭虹. 一种基于短LT码的级联编译码算法[J]. 数据采集与处理, 2014, 29(3):445-450.

Huang Xiaoke, Liu Luokun, Guo Hong. A concatenated coding algorithm based on LT codes with small message length[J]. Journal of Data Acquisition and Processing, 2014, 29(3): 445-450.

[5] 徐大专, 邵汉钦, 张小飞,等. 数字喷泉码及网络喷泉码的最新进展[J]. 数据采集与处理, 2014, 29(3):351-359.

Xu Dazhuan, Shao Hanqin, Zhang Xiaofei, et al. Recent research progress on digital fountain codes and network fountain codes [J] . Journal of Data Acquisition and Processing, 2014, 29(3): 351-359.

[6] Luby M. LT codes[C]∥The 43rd Annual IEEE Symposium on Foundations of Computer Science. Vancouver, BC, Canada: IEEE, 2002:271-280.

[7] Nguyen T D, Yang L L, Hanzo L. Systematic Luby transform codes and their soft decoding [J]. IEEE Workshop on Signal Processing Systems, 2007,67-72.

[8] Nguyen T D, Yang L L, Ng S X, et al. An optimal degree distribution design and a conditional random integer generator for the systematic Luby transform coded wireless internet [C]∥Wireless Communications and Networking Conference. Las Vegas, NV, USA:IEEE, 2008,243-248.

[9] Yuan Xiaojun,Li Ping. On systematic LT codes [J]. IEEE Commun Lett, 2008,12(9):681-683.

[10] Yuan Xiaojun, L Ping. Quasi-systematic doped LT codes [J]. IEEE J Sel Areas Commun, 2009,27(6): 866-875.

[11] Hayajneh K F, Yousefi S. Improved systematic fountain codes in AWGN channel [C]∥13th Canadian Workshop on Information Theory.[S.l.]:IEEE, 2013:148-152.

[12] Luby M G, Mitzenmacher M, Shokrollahi M A. Analysis of random processes via AND-OR tree evaluations[C]∥Proceedings of the 9th Annual ACM-SIAM Symposium on Discrete Algorithms．New York, USA:Society for Industrial & Applied Mathematics,1998:364-373.

[13] Sejdinovic D, Piechocki R J, Doufexi A. AND-OR tree analysis of distributed LT codes[C]∥Networking and Information Theory, IEEE Information Theory Workshop on. Volos, Greece: IEEE, 2009:261-265.

AsymptoticPerformanceAnalysisandDegreeDistributionDesignforSystematicLubyTransformCodesoverBinaryErasureChannel

Hua Jie1，2， Xu Dazhuan1，2， Xu Shengkai1，2

(1.Jiangsu Key Laboratory of Internet of Things and Control Technologies, Nanjing University of Aeronautics and Astronautics, Nanjing, 211106, China;2.College of Electronic and Information Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing,211106, China)

The asymptotic performance formula of systematic LT codes(SLT) in binary erasure channel (BEC) is firstly derived based on AND-OR tree analysis and its lower limit is given. Simulation results show that the actual bit error ratio(BER), the asymptotic performance and the lower limit match each other perfectly when the overhead is large enough. Then the optimization of degree distribution is proposed by the improved systematic linear programming(ISLP) model in accordance with the asymptotic performance. The optimized degree distribution is obviously superior to robust soliton distribution(RSD) and truncated degree distribution(TDD). Furthermore, the asymptotic behavior of the optimized degree distribution can be controlled by the given overhead and BER. In other words, the ideal BER can be obtained within the overhead we want, which also influences the overhead for complete decoding. Simulation results show that the overhead required for data recovery is close to that of we set. The comparison of BER, the overhead required for data recovery and the time of encoding and decoding for LT codes and SLT codes show that SLT codes have better performance than LT codes with more quick speed in data recovery.

asymptotic behavior; degree distribution; linear optimization; systematic LT codes

国家自然科学基金(61471192, 61371169)资助项目；江苏省普通高校研究生科研创新计划(SJLX15_0120)资助项目；中央高校基本科研业务费专项资金资助项目。

2016-03-01；

2016-08-30

TN929.5