基于可信性理论的微网动态有功优化控制*

董萍 秦川 冯永青

(1.华南理工大学 电力学院， 广东 广州 510640； 2.中国南方电网电力调度控制中心， 广东 广州 510623)

基于可信性理论的微网动态有功优化控制*

董萍1秦川1冯永青2

(1.华南理工大学 电力学院， 广东 广州 510640； 2.中国南方电网电力调度控制中心， 广东 广州 510623)

针对包含多种分布式电源的微网并网运行系统，应用可信性理论分析法，建立了包含分布式电源的微网并网运行系统的动态有功优化模型，以微网运行的费用成本最小化作为目标函数，求解后将其结果与采用场景法处理随机变量的优化方法所得结果进行对比.算例分析验证了所提模型的正确性，以及所述方法和求解算法对处理小规模分布式电源接入微网有功优化问题的有效性和实用性.

分布式电源；微网并网运行系统；模糊参数表示法；场景法；可信性理论

随着《关于进一步深化电力体制改革的若干意见》(中发〔2015〕9号)[1]及其相关配套文件的颁布，电力体制改革正逐步推进.开放电网无疑为微网与电力系统联接提供了很大机遇.在微网的经济调度问题中，相关文献对一些包含多种分布式电源的冷热电联调度[2]及热电负荷[3- 5]的微网系统，在并网运行和孤岛运行方式下，系统中各电源有功出力和无功出力的经济运行展开了研究，但上述文献中所建立的系统模型未考虑具体微网的结构或未对微网的并网模式建立具体的经济运行模型.文献[6]分别在微网并网和孤岛运行模式下，建立了微网动态经济调度模型，对微网中的风电随机性采用场景分析法处理，求解含风电随机性的微网经济调度问题.

在微网内的分布式电源中，风电以及光伏发电出力包含了随机性和模糊性.以风电为例，风电出力准确而言是同时包含随机性和模糊性的不确定量，其出力的随机性直观地表现为风速的随机性，大量实测数据的统计表明，风速是近似服从Weibull分布[7- 8]的随机变量，但如果结合风电场所处环境、天气等外部因素，对风速预测的准确性下降，加之进入风电场之后所存在的涉及空气动力学的现象(例如尾流效应)，机组之间所获得的实际风速不同，风电的实际出力与将风速的实际测量值(或者预测值)结合风机功率曲线得到的出力之间必然存在一定的误差.对风速测量的不精确，以及受风电场所处地理环境、风场之中的尾流效应等外部因素的影响，难以用风速变化来描述和估计变量，使得风电出力必然存在模糊性.而现有的预测方法可靠性低，导致工程运行存在实际问题，这也表明对模糊性的考虑很有必要，虽然国外已经开展了预测风电场发电出力的研究工作[9- 10]，也已有多种预测方法[11]，但实际出力与预测值之间仍然存在很大误差.

在传统的研究中，关注不确定因素的随机性较多，较少考虑了到模糊性.再者，传统研究方法即使考虑了问题的模糊性，也无法将随机性与之同时分析.Liu[12]利用测度论建立了基于可信性测度的完善的公理化基础.可信性理论是研究模糊事件行为的数学分支，在研究模糊性的过程中得到推动，并形成了完善的公理化体系[13]，由于概率论和模糊论均是建立在测度论的基础上，因此这个公理化体系包含了随机模糊双重不确定分析的方法.同时文献[14]对可信性理论处理随机模糊等多重不确定性问题进行了说明.文献[15]中提出了一个包含风电的经济调度模型，将模糊论初步应用于经济调度，但该模型相对简单，同时也仅应用了模糊论去处理不确定性.文献[16- 17]将风电出力的模糊性转化为其出力的预测误差的模糊性，应用可信性理论推导了风电预测误差的可信性分布函数，并建立了含模糊参数的模糊机会约束模型，但只考虑了风电这类分布式电源出力的模糊性，没有考虑其他分布式电源出力的不确定性对研究问题的影响.

随机优化中，基于机会约束理论的随机优化是常见的处理不确定性的方法[18]，应用概率形式描述分布式电源的出力的随机性，将分布式电源出力的概率满足置信水平的约束作为模型的运行约束，通过抽样多次求解模型并判断，最终求取满足条件的样本期望.此外还有机会规划约束方法[19]，该方法通常采用抽样平均近似法(SAA)将不确定的机会约束转换为可计算的确定性约束，求解确定性模型.此时机会约束置信水平以及抽样次数对结果均有影响，这两个过程都对不确定性问题中的随机性进行了处理.

考虑到不同时间断面的耦合性，文中主要研究包含风电以及光伏发电多种分布式电源的微网并网运行系统的动态有功优化调度问题.基于可信性理论，考虑分布式电源出力的不确定性，采用梯形模糊数表示每个优化时段分布式电源的出力，以最小化微网运行的费用成本作为目标函数进行优化，建立了包含分布式电源的微网并网运行系统的动态有功优化模型，采用通用代数建模软件GAMS框架下的CONOPT求解器，结合随机模糊期望值的求解，通过算例的计算，对文中方法的可行性和有效性进行验证.

1 系统模型

文中采用的与微网并网运行的系统为美国PG&E69节点配电系统[20].配网系统的节点1与大电网联接，根据配网系统提供的负荷数据[21]，选取负荷较大的节点50作为微网与配网系统联接的节点.微网并网运行时，整个系统简单接线图如图1所示.

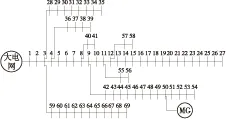
图1 微网并网系统的接线简图

Fig.1 Connection diagram of microgrid connected to distribution system

微电网的结构如图2所示.变压器仅考虑串联等效电阻RT和电抗XT，而忽略了并联等效参数GT和BT.在微网系统内，常规机组的容量为600 kW，爬坡约束为300 kW，风电容量为200 kW；光伏发电1的容量为950 kW，均位于节点1；光伏发电2的容量为50 kW，位于节点9.

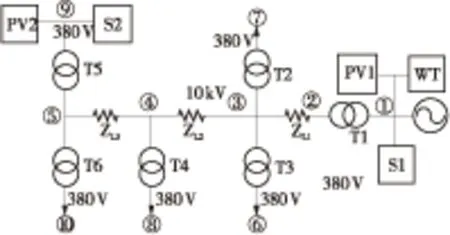
图2 10节点微网系统接线图

微网与配网系统存在双向交易.同时，根据电力体制改革相关内容，微网享有一定的国家政策扶持，即为微网系统内的分布式电源出力实施货币补贴.在此背景下，将微网的运行成本作为目标函数进行优化求解，构造了微网并网运行系统有功优化的数学模型：

minf=C1+C2+C3

(1)

其中，C1为微网系统内所有常规机组在全部调度时段中的费用成本总和，C2为分布式电源的出力补贴[21]，C3为微网与配网之间交互成本.则有：

(2)

(3)

(4)

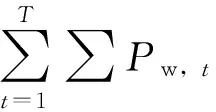
1.1 微网元件的约束

常规可控机组、储能设备以及微网结构的约束条件为：

(5)

(∀g∈G,∀t∈T)

(6)

(∀g∈G,∀t∈T)

(7)

(∀b∈Nb,∀t∈T)

(8)

(∀b∈Nb,∀t∈T)

(9)

(∀b∈Nb,∀t∈T)

(10)

(∀b∈Nb,∀T′∈T)

(11)

(∀i∈N,∀t∈T)

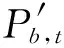
1.2 微网并网系统的约束

配网部分的约束如下：

(12)

(13)

式(12)表示配网系统内各个节点的有功潮流约束.式(13)表示各个节点的电压上、下限约束.Pks,t表示节点k在时刻t的注入功率，Vk,t是节点k在时刻t的节点电压，θkl,t是节点k，l之间相角的差值，Gkl和Bkl则表示配网系统节点导纳矩阵的实部和虚部.

将微网系统与配网系统的数学模型相结合，以微网系统中的节点5作为并网接线端,通过变压器与配网联接实现并网运行.通过以下处理方式实现，在微网中引入与配网的交互功率Pline计入微网的有功潮流约束方程(11)之中，作标幺值统一处理.配网系统中，在微网并网的节点同样引入与微网的交互功率Pline计入配网的有功潮流约束方程(12)之中.

配网系统与大电网系统通过变压器联接，采用与微网并网相同的处理方法，引入配网系统与大电网之间的传输功率PL，令传输功率PL只能从大电网注入配网系统，即令PL只可取正值.

2 分布式电源出力不确定性的处理方法

2.1 可信性理论分析法

可信性理论是综合处理考虑变量随机性及模糊性双重不确定性的数学方法，其中，模糊性为因缺乏精确测量的工具无法精确定义导致的不确定性.文中应用模糊参数构建的分布式电源出力模型，结合其所处环境特有的地理气候等外部因素，将分布式电源出力描述为随机模糊变量，在随机性的基础上以模糊性加以完善，即是可信性理论对不确定问题的分析思路.

文中应用可信性分析法时，根据分布式电源出力的历史数据，通过模糊参数构建的出力模型，综合了其自身特有的外部因素，在此基础上，再进行随机抽样，认为此出力模型所描述的样本区间满足随机分布.与直接对未经处理的历史数据进行抽样的随机处理方法相比，综合了自身的特性，相对完善和严谨.以风电为例，文中根据风速的隶属度函数以及风机功率曲线，结合随机分布函数，构建出风电出力的不确定模型，即得到风电出力的可信性分布函数[22- 23]，如图3所示.由图3可见，该可信性分布函数与标准的梯形模糊数隶属度函数类似，稍有差别.

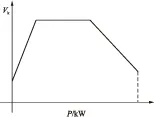
图3 可信性分布函数

2.2 可信性理论分析方法的应用实现

基于可信性理论，采用模糊模拟技术[13]，构建分布式电源出力的不确定模型，求取模型中常规机组出力方案的随机模糊期望值[24]，计算流程如图4所示，图中M为抽样次数，∧为最小化算子，∨为最大化算子.求解步骤如下：

步骤1 设置抽样次数.根据分布式电源输出的平均功率，在可信性分布函数的出力区间随机产生M个样本，作为风机和光伏的M个出力情况，而这个区间内的样本取值满足随机分布.

步骤2 计算样本出现的可信度.根据步骤1中得到的样本、可信性分布函数，计算得到该样本出现的可信度.

步骤3 循环求解有功优化模型.根据步骤1中得到的分布式电源出力情况，将每一个出力作为参数，重复在通用代数建模软件GAMS上求解，得到分布式电源M个出力情况下相应的目标函数值.以及常规机组的出力方案.

步骤4 计算常规机组出力的随机模糊期望值.根据步骤2中得到的可信度，以及流程图计算得到一次随机模糊期望值，重复以上过程M次，将M个期望值累加，得到最终的随机模糊期望值，从而可得最终优化后的常规机组出力方案.

步骤5 求解有功优化模型的期望目标函数值.根据常规机组的出力方案的期望值，通过费用函数计算可得相对应的成本，同理，重复步骤4得出分布式电源出力方案的期望值以及配网与微网之间交互功率的期望值，并计算得出相应费用成本，最终可得目标函数值的期望值.

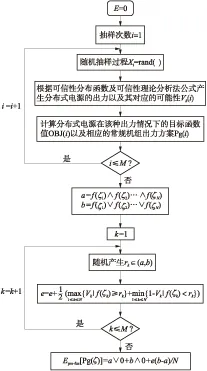
图4 可信性理论分析法应用流程图

3 算例与分析

配网系统的节点1与大电网联接，将微网与配网系统的节点50联接.采用通用代数建模软件GAMS框架下的CONOPT求解器，在求解文中有功优化问题时，得出相应出力方案的同时，系统运行点的潮流信息均可在求解器的结果列表查到.

3.1 不同模糊数表示不确定性的计算结果

为研究上述几种模糊数表示的差异性，采用不同的模糊数表示，取不同的样本数(分别为10、20、50和100)，并在前述的系统模型上分别进行计算，结果如图5所示.根据前述随机模糊期望值的计算流程,得出3种模糊数表示下相应的常规机组出力方案，如图6所示.

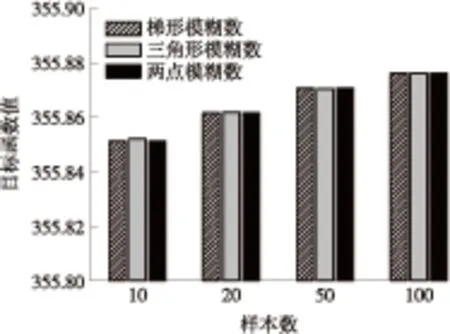
图5 不同模糊数表示下的目标函数值计算结果

Fig.5 Results of objective function values with different fuzzy parameters

从图5可知，采用不同模糊数表示得到的目标函数值差别很小，而采用同一种模糊数表示时不同样本数所得结果差别也很小，说明采用不同模糊数处理不确定性的差异较小，从常规机组的出力方案结果也可看出.

同样，根据计算流程，分布式电源出力方案在不同模糊数表示下的结果差异也很小.同时，由图6可见，可信性理论分析法在求解问题时受样本数影响较小，实验过程中取更大的样本数时得出的结果与文中已列出的结果基本相似，由此可知，求解结果受样本数影响较小，因此更大样本数的求解结果在文中不再列出.考虑到分布式电源出力的不确定性与负荷不确定性具有一定程度的相似性，参考现有文献中处理负荷不确定性的方法，且由于梯形隶属度函数与人们研究不确定性问题的思考方式很相近，因此，文中之后应用可信性理论的求解均采用梯形模糊函数来表示分布式电源的出力不确定性.

3.2 不同的处理不确定性方法的计算结果

为验证可信性理论分析法的有效性，应用场景分析法的求解结果与可信性理论分析法的求解结果进行对比.在场景分析法中，场景数通常取为10、20、50，在产生误差场景数目较大时，如达到数百甚至上千数量级时，一般会采用场景缩减法选取其中具有代表性的场景进行计算.因此分别在预测场景基础上产生10、20、50个误差场景进行求解.同时，采用相同的系统模型以及系统内各部分相同的参数设置，应用可信性理论分析法，取样本数为10、20和50与之对应，得到不同样本数目的优化结果，并与场景分析法的结果对比，如图7所示.

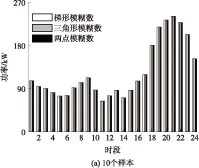
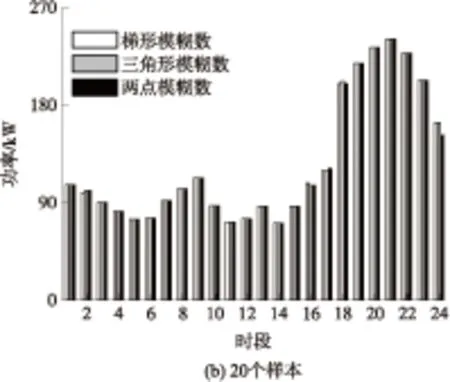
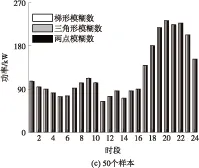
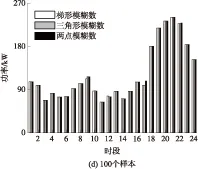
图6 不同模糊数表示下的常规机组出力方案

Fig.6 Outputs plan of conventional power unit with different fuzzy parameters

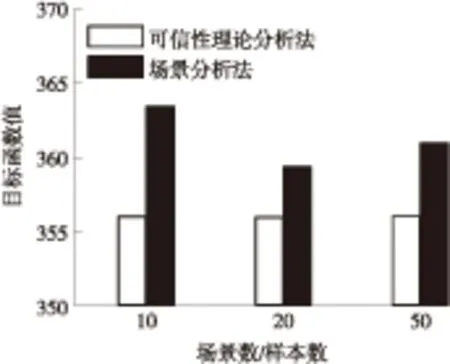
图7 不同的处理不确定性方法下目标函数值计算结果

从图7可以看出，两种方法得到的结果相近，由此可验证可信性理论分析法处理不确定性问题的有效性，且从本次计算结果可看出可信性理论分析法的优化效果较好.通过表1可以很直观地看出，场景分析法随着场景数增加计算耗时增加较快.应用场景分析法需对系统模型进行修正，可信性理论分析法提供了一种简化且有效的方式，在计算耗时上也展现了一些优势.

表1 不同的处理不确定性方法下计算用时

Table 1 Results of elapsed time to solve program with different methods dealing with uncertainty

场景数/样本数计算时长/min场景分析法可信性理论分析法10752025185013453

此外，场景分析法在生成误差场景时，没有相应求取误差场景发生概率的过程，因而求解结果并未考虑每个场景发生概率的影响.而可信性理论分析法每次随机产生的样本均可计算其对应的可信度，对最终的目标函数值产生作用，一定程度上减小了局限性，更符合实际情况.

3.3 采用不同渗透率的微网的计算结果

增加分布式电源的容量，以改变微网在配网系统中的渗透率，重新在前述的算例系统应用动态有功优化数学模型求解.处理后的微网，其常规机组的容量和爬坡约束不变，风电容量增加为0.8 MW、光伏发电1容量增加为3.8 MW、光伏发电2容量增加为0.2 MW.文中令处理后的微网并网运行的算例系统为高渗透率系统(以下简称为系统2)，未处理的微网并网运行的原算例系统为低渗透率系统(以下简称为系统1).

在系统2中进行计算，得到场景分析法和可信性理论分析法取不同场景数/样本数的结果，如表2所示.

表2 两种方法目标函数值计算结果

Table 2 Results of objective function values with different methods

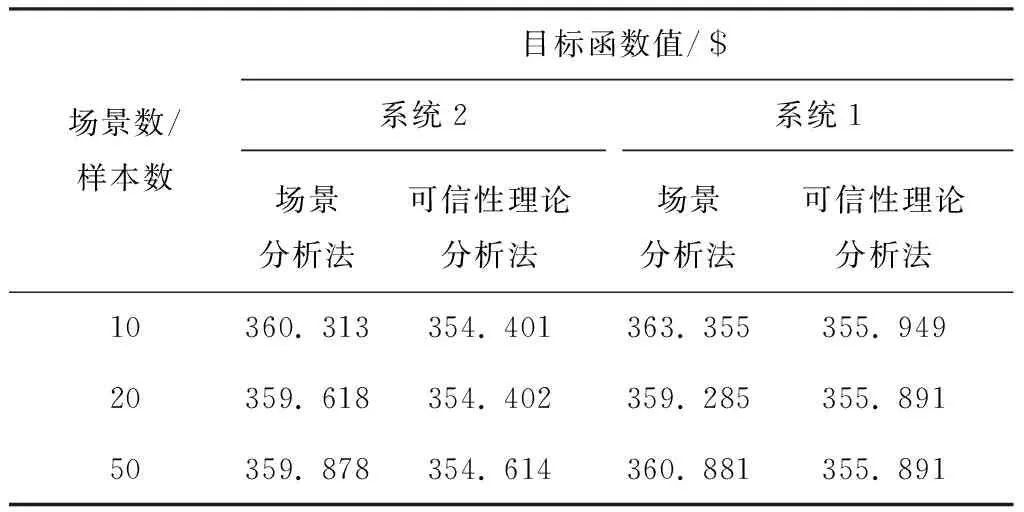
场景数/样本数目标函数值/$系统2场景分析法可信性理论分析法系统1场景分析法可信性理论分析法10360.313354.401363.355355.94920359.618354.402359.285355.89150359.878354.614360.881355.891

两种方法在渗透率不同的系统中求解的常规机组出力结果如图8所示.

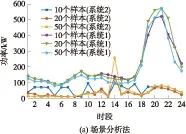
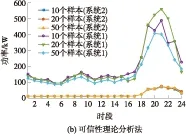
图8 不同渗透率的微网中常规机组出力结果

Fig.8 Outputs of conventional power unit of different microgrids

由图8可知，当微网的渗透率较大，即分布式电源出力较大时，两种方法常规机组出力相应减小.但此时可看出，在微网的渗透率增大时，场景分析法在不同场景数下得到的常规机组出力差异较为明显，而可信性理论分析法在不同样本数下的结果差别很小、基本一致.可见当微网的渗透率逐渐变大时，即当分布式电源带来的不确定性增加时，可信性理论分析法的求解结果受样本数影响较小，整体表现出较稳定的求解效果.

4 结论

结合电力体制改革的相关背景，在原本确定性的有功优化模型上进行改进，建立了包含分布式电源的微网并网运行系统的动态有功优化模型，并基于可信性理论，采用梯形模糊数表示分布式电源出力的不确定性，应用通用代数建模软件GAMS多次求解，得到以下主要结论：

(1)可信性理论分析法中，3种不同模糊数处理不确定性所得结果相差很小，对于每种模糊数而言，样本数的大小对求解结果影响较小.

(2)通过与场景分析法对比，可信性理论分析法在处理不确定性方面，提供了一种简化、有效的处理方式，同时避免了一些场景分析法处理不确定问题的局限性，在计算耗时上可信性理论也体现出一定的优势.

(3)在微网的渗透率变大时，应用场景分析法取不同场景数得到的常规机组出力差异较为明显；而应用可信性理论分析法得到的结果受样本数影响较小，可见可信性理论分析法在应对不确定性增加的问题时，展现出了更好的解决能力.

[1] 中国共产党中央委员会，中华人民共和国国务院.关于进一步深化电力体制改革的若干意见(中发〔2015〕9号) [Z].北京：中国共产党中央委员会，中华人民共和国国务院，2015.

[2] 韩宏飞.分布式电源协调优化调度 [D].北京：华北电力大学，2014.

[3] 陈洁，杨秀，朱兰，等.微网多目标经济调度优化 [J].中国电机工程学报，2013，33(19)：57- 66.

CHEN Jie，YANG Xiu，ZHU Lan，et al.Microgrid multi-objective economic dispatch optimization [J].Proceedings of the CSEE，2013，33(19)：57- 66.

[4] 陈洁，杨秀，朱兰,等.基于遗传算法的热电联产型微网经济运行优化 [J].电力系统保护与控制，2013，41(8)：7- 15.

CHEN Jie，YANG Xiu，ZHU Lan，et al.Genetic algorithm based economic operation optimization of a combined heat and power microgrid [J].Power System Protection and Control，2013，41(8)：7- 15.

[5] 陈洁，杨秀，朱兰，等.不同运行调度模式下微网经济运行对比分析 [J].电力自动化设备，2013，33(8)：106- 113.

CHEN Jie，YANG Xiu，ZHU Lan，et al.Comparison of microgrid economic operation among different dispatch modes [J].Electric Power Automation Equipment，2013，33(8)：106- 113.

[6] 陈涛.微电网经济调度问题研究 [D].广州：华南理工大学，2013.

[7] 丁明，吴义纯，张立军.风电场风速概率分布参数计算方法的研究 [J].中国电机工程学报，2005，25(10)：107- 110.

DING Ming，WU Yi-chun，ZHANG Li-jun.Study on the algorithm to the probabilistic distribution parameters of wind speed in wind farms [J].Proceedings of the CSEE，2005，25(10)：107- 110.

[8] HETZER J.YUS D C.An economic dispatch model incorporating wind power [J].IEEE Transactions on Power Energy Conversion，2008，23(2)： 603- 611.

[9] CONTAXIS G C，KABOURIS J.Short term scheduling in a wind/diesel autonomous energy system [J].IEEE Transactions on Power Systems，1991，6(3)：1161- 1167.

[10] ALEXIDIS M C，DOKOPOULOS P S，SAHSAMANOGLOU HS.Wind speed and power forecasting based on spatial correlation models [J].IEEE Transactions on Energy Conversion，1999，14(3)：836- 842.

[11] 康重庆，夏清，张伯明.电力系统负荷预测研究综述与发展方向的探讨 [J].电力系统自动化，2004，28(17)：1- 11.

KANG Chong-qing，XIA Qing，ZHANG Bo-ming.Review of power system load forecasting and its development [J].Automation of Electric Power Systems，2004，28(17)：1- 11.

[12] LIU B.Uncertainty Theory：an introduction to its axiomatic foundations [M].Berlin:Springer-Verlag，2004.

[13] 刘宝碇，彭锦.不确定理论教程 [M].北京：清华大学出版社，2005：74- 128.

[14] LIU B.Theory and practice of uncertain programming [M].Heidelberg：Physical Verlg，2002.

[15] VIADIMIRO Miranda，PUN Sio Hang.Economic dispatch model with fuzzy wind constrains and attitudes of dispatches [J].IEEE Transactions on Power Systems，2005，20(4)：2143- 2145.

[16] 艾欣，刘晓.基于可信性理论的含风电场电力系统动态经济调度 [J].中国电机工程学报，2011，31(增刊)：12- 18.

AI Xin，LIU Xiao.Dynamic economic dispatch for wind farms integrated power system based on credibility theory [J].Proceedings of the CSEE，2011，31(Suppl)：12- 18.

[17] 艾欣，刘晓，孙翠英.含风电场电力系统机组组合的模糊机会约束决策模型 [J].电网技术，2011，35(12)：202- 207.

AI Xin，LIU Xiao，SUN Cui-ying.A fuzzy chance constrained decision model for unit commitment of power grid containing large-scale wind farm [J].Power System Technology，2011，35(12)：202- 207.

[18] 张贞.基于机会约束理论的微电网随机优化调度 [J].电力学报，2013，28(2)：135- 139.

ZHANG Zhen.Stochastic optimization dispatch of micro-grid based on the chance constraint theory [J].Journal of Electric Power，2013，28(2)：135- 139.

[19] 杨洪明，王爽，易德鑫，等.考虑多风电场出力相关性的电力系统随机优化调度 [J].电力自动化设备，2013，33(1)：114- 120.

YANG Hong-ming，WANG Shuang，YI De-xin，et al.Stochastic optimal dispatch of power system considering multi-wind power correlation [J].Electric Power Automation Equipment，2013，33(1)：114- 120.

[20] 曾学强.含风电机组的配电网无功优化及算法研究 [D].成都：西南交通大学，2011.

[21] 国家发展改革委.关于深圳市开展输配电价改革试点的通知(发改价格[2014]2379号) [Z].北京：国家发展改革委，2014.

[22] LIU Baoding.Toward fuzzy optimization without mathe-matical ambiguity [J].Fuzzy Optimization and Decision Making，2002，1(1)：43- 63.

[23] 杨毅，韦钢，周冰,等.含分布式电源的配电网模糊优化规划 [J].电力系统自动化，2010，34(13)：19- 23.

YANG Yi，WEI Gang，ZHOU Bing,et al.Optimized fuzzy planning of the distribution network including distributed generation [J].Automation of Electric Power Systems，2010，34(13)：19- 23.

[24] 熊虎，向铁元，陈红坤，等.含大规模间歇式电源的模糊机会约束机组组合研究 [J].中国电机工程学报，2013，33(13)：36- 44.

XIONG Hu，XIANG Tie-yuan，CHEN Hong-kun，et al.Research of Fuzzy chance constrained unit commitment containing large-scale intermittent power [J].Proceedings of the CSEE，2013，33(13)：36- 44.

DynamicActivePowerOptimizationControlofMicrogridontheBasisofCredibilityTheory

DONGPing1QINChuan1FENGYong-qing2

(1. School of Electric Power, South China University of Technology, Guangzhou 510640, Guangdong, China;2. CSG Electric Power Dispatching Control Center, Guangzhou 510623, Guangdong, China)

Aiming at the microgrid parallel operation system containing various distributed generations, a credibility theoretical analysis is made to establish a dynamic active power optimization model. Then, by taking the minimum microgrid operation cost as the objective function, the model is solved and the results are compared with those obtained by the optimization via scenario analysis. Calculation example verifies the correctness of the proposed model, as well as the effectiveness and practicability of above-mentioned method in dealing with the active power optimization of microgrid containing various small-scale distributed generations.

distributed generation; microgrid parallel operation system; fuzzy parameter representation; scenario method; credibility theory

2016- 10- 26

国家重点基础研究发展计划 (973计划) 项目(2013CB228205)；国家自然科学基金资助项目(51107042)；华南理工大学中央高校基本科研业务费专项资金重点资助项目(2015ZZ017)

*Foundationitems： Supported by the National Program on Key Basic Research Project of China(973 Program)(2013CB228205)and the National Natural Science Foundation of China(51107042)

董萍(1978-)，女，博士，副教授，主要从事FACTS技术及电力系统优化与控制研究.E-mail：epdping@scut.edu.cn

1000- 565X(2017)07- 0008- 08

TM 727

10.3969/j.issn.1000-565X.2017.07.002