一种基于ICDF的支持向量机参数快速优化方法*
2017-12-15王加朋胡跃明罗家祥
王加朋 胡跃明 罗家祥
(华南理工大学 自动化科学与工程学院, 广东 广州 510640)
一种基于ICDF的支持向量机参数快速优化方法*
王加朋 胡跃明 罗家祥†
(华南理工大学 自动化科学与工程学院, 广东 广州 510640)
在高斯核支持向量机 (SVM) 的参数优化中, 针对以特征空间中的类间距离 (ICDF)为测度选择核参数时存在计算量大、耗时长的问题, 首先提出并证明了ICDF是高斯核参数的严格单峰正定函数, 然后根据该结论提出了改进黄金分割法(MGSA)来快速搜索核参数在候选集中的最佳值, 在此基础上提出一种基于MGSA和微分进化算法的SVM参数快速优化方法, 最后通过比较实验验证了所提方法的有效性和快速性.
支持向量机;类间距离;参数优化;核参数;改进黄金分割法
支持向量机[1](SVM)作为一种高效的分类技术已被广泛应用在图像分类[2]、生物医学[3]、文本分类[4]、故障诊断[5]、人脸表情识别[6]和电缆温度计算[7]等领域.SVM使用核函数在高维特征空间寻找分离超平面,无论核函数形式如何,核参数影响着SVM的分类性能[8- 9].文中关注应用广泛的高斯核SVM[10].文献[11]指出了高斯核参数γ能够测量数据在高维特征空间的分离性,以及惩罚因子C控制平衡SVM的误差项和泛化能力,因此选择最佳参数组合是建立高效分类性能SVM模型的重要保障.
学者们已研究了较多SVM的参数选择方法.网格搜索法(GS)是传统的直接方法[12],因其对所有离散划分参数组合的模型进行训练比较,该方法计算量大,且很难确定合适的步长[9].文献[9,13- 16]通过对SVM泛化误差构建估计函数或上界提出一些数值方法,尽管这些方法比网格法搜寻速度更有效,但由于这些泛化上界的非凸性,它们对初值特别敏感,极易陷入局部最优并且要求这些上界必须是可微的.为了克服这些困难,进化算法[17- 19]由于对非凸函数具有很好的全局搜索能力而被用来优化SVM参数,但这些技术在种群进化迭代中需训练大量的SVM模型[11],仍然要耗费大量计算,特别是参数范围较大时尤为突出.
为减少训练SVM次数,依据显著分离的特征空间对SVM分类性能的紧密相关度[8- 11]和特征空间中的类间距离(ICDF)可以度量特征空间中各类分离程度[20],文献[11]首次研究了使用一些ICDF作为测度指标来选择高斯核参数,该方法首先将ICDF最大值对应的参数作为最佳核参数,然后与候选惩罚因子C值组合训练SVM模型选择最好的C值.结果表明该方法与GS有相似的性能但消耗时间明显减少,因该方法大量减少了SVM模型的训练次数.然而由于需要对核参数候选集依次计算ICDF值来确定最优核参数,除了很难确定合适的采样步长外[8],该方法会遗漏搜索参数区间中可能最优的连续值.
针对上述存在大量计算ICDF值的问题,并结合进化算法可搜索参数连续值的优点[21],文中提出了一种基于ICDF的SVM参数快速优化方法.首先证明了ICDF是关于高斯核参数的严格单峰正定函数;然后根据该结论提出了改进黄金分割算法(MGSA)在核参数大区间候选离散值集中快速搜索最佳值,并结合MGSA和进化算法给出了一种快速搜索SVM参数的混合方法框架;最后具体选择一种自适应进化算法(SADE)[22]进行试验,以验证所提算法的有效性.
符号和假定:sgn( )是符号函数;‖ ‖表示Euclidean范数;x=0+表示x是正的且从右边趋向于0;x=+∞表示x是正的且趋向于正无穷大;U(a,b)表示a的b邻域,即{x|a-b 本节对SVM及其参数优化问题作简要的介绍,详细内容可参考文献[1],给定训练样本数据和类别标签对(xi,yi),其中i=1,2,…,l,xi是n维训练数据,类别标签yi∈{+1,-1}.SVM基本思想是将训练样本通过非线性映射φ(·)映射到高维Hilbert空间中,从而在这种高维特征空间中构建最佳判别超平面函数为式(1): f(x)=sgn(wTφ(x)+b) (1) 其中,w表示垂直于最佳分离超平面的权值向量,b为偏置项.根据统计学习理论,最优的参数w和b,可通过最小化式(2)结构风险得到: (2) s.t.yi(wTzi+b)≥1-ξi,ξi≥0. 其中,zi=φ(xi)是映射到高维空间的高维特征向量,C>0为惩罚因子,ξi为松弛变量. 为了得到分离超平面,可以通过求解上述问题(2)的对偶问题(3)来解决: (3) s.t. 0≤αi≤C,yTα=0. (4) 核函数有多种形式[11],文中仅研究应用广泛的高斯核,表达如式(5)所示. K(x,xi)=e-γ‖x-xi‖ (5) 文献[9,11]指出高斯核参数决定了数据映射到高维特征空间的分离性,惩罚因子平衡SVM训练误差项和泛化能力,因此这两个参数的选择直接影响SVM的性能,文中研究有效选择最优的参数组合的方法. 文献[11,20]对以样本数据在特征空间中的类间距离(ICDF)作为选择高斯核参数的度量指标已做了相关研究,指出了以两类样本在高维特征空间中对应中心点的Euclidean距离作为指标分类效果更好,文中研究采用这一指标,同样记为ICDF,对于两类数据x和y,特征空间中的类间距离计算如式(6)所示.将核函数式(5)代入式(6)中可得特征空间中的距离函数ICDF关于高斯核参数的表达式(7). (6) (7) 在利用ICDF进行SVM核参数选择时,当前研究方法[11,20- 21]是将给定的核参数大区间[2-L,2L](其中L为足够大正整数)离散化为候选值集{2-L,2-L+1,…,2L},然后依次计算每个候选值相应的距离函数ICDF值,选取最大ICDF值对应的候选值为最好核参数,这种方法简记为ICDF-one-by-one.该方法需要大量计算ICDF函数值,且单次计算式(7)的复杂度是O(max{m2,mn,n2}),当训练样本较多时,计算量大且耗时长.针对该不足,文中将研究ICDF与核参数的性质并提出在离散候选集中快速选择核参数最优值的MGSA法;此外,为防止遗漏搜索更好的连续值,将借鉴文献[21]缩短搜索区间(覆盖候选集中性能最优核参数)的思想,结合MGSA和进化算法设计一种快速搜索SVM最优参数组合的混合方法框架. 定义1[23]设函数g(x):R→R,闭区间[a,b]⊆R,如果存在β∈[a,b],使得g(x)在[a,β]上严格单调递增(或严格单调递减)且在[β,b]上严格单调递减(或严格单调递增),那么称函数g(x)为在区间[a,b]上的严格单峰函数,区间[a,b]是函数g(x)严格单峰区间. 引理1[24](Rolle’s Theorem定理)如果实值函数f(x)在闭区间[a,b]上是连续的,在开区间(a,b)是连续可微的,且f(a)=f(b),那么至少存在一个c∈(a,b)数使得导数f′(c)=0. 定理1 对在高维特征空间线性可分的两类,距离函数ICDF(式(7))是关于高斯核参数的严格单峰正定函数,即距离存在唯一最大值点,设在γ0处取得,距离函数在区间(0,γ0)上严格单调递增,在区间(γ0,+∞)上严格单调递减. 证明根据距离函数式(6)的定义表达式,由数学知识很容易知道距离函数式(7)关于高斯核参数在区间(0,+∞)是非负、连续和可微的. d(γ)>0 (8) 对距离函数(式(7))计算两个极限值,容易得到式(9)和式(10): d(0+)>0 (9) d(+∞)>0 (10) 根据距离函数式(7)的连续性质,对于给定一个任意小正数ε,必存在两个数σ1、σ2,分别位于邻域σ1∈U(0,δ1)和区间σ2∈U(δ2,+∞),其中0<δ1≤δ2,使得 d(σ1)=ε (11) d(σ2)=ε (12) 此时对距离函数(式(7))在区间(σ1,σ2)上应用引理1,则至少存在一个正数ξ∈(σ1,σ2),使得距离函数式(7)在此点的导数为零,得到式(13): d′(ξ)=0 (13) 式(13)中导函数计算如式(14): (14) (15) (16) 注意到指数函数E(γ)=e-γ在区间(0,+∞)上严格单调递减,且值域为(0,1).这一性质在下面推导中要使用. 首先考虑在区间(ξ,+∞)上Γ(γ)的符号,设对于给定任意正数Δ>0, (17) 第一个小于号利用指数函数的上述性质,第二个等号是将式(16)移项代入计算得到,最后一步使用指数函数的上述性质,从等式(14)可以看出,距离函数导数的符号和式(15)所示的Γ(γ)的符号相同,在区间(ξ,+∞)上,根据式(17)可知Γ(γ)<0,所以在该区间有d′(γ)<0,说明距离函数式(7)在该区间(ξ,+∞)上严格单调递减. 同理,可以类似地推导出在区间(0,ξ)上,Γ(ξ-Δ)>0,所以有d′(γ)>0,说明距离函数(式(7))在该区间(0,ξ)上严格单调递增.综上所述,根据定义1,距离函数(式(7))在(0,+∞)上是严格单峰正定函数,且在γ0=ξ处取得唯一最大值.证毕. 考虑在给定高斯核参数的大区间[2-L,2L](其中L为足够大正整数)上,之前的搜索方法是将该区间离散化为候选值集{2-L,2-L+1,…,2L},然后依次计算距离ICDF函数值,选取其最大值对应的核参数.根据定理1的结论,距离函数ICDF式(7)是高斯核参数的严格单峰正定函数,可以用线性搜索算法,考虑到黄金分割法(GSA)[25]无需计算导数信息,为了可以搜索候选离散整数值,提出一种修改GSA算法(Modified Golden Section Algorithm,MGSA)来快速解决这一问题,减少计算量. 设φ(x)=-d(2x),因此最大化距离函数d(2x)也就等价于最小化φ(x),令a1=-L,b1=L,MGSA流程如下. 算法1 MGSA. 步骤1 初始化k=1,设置初始区间[a1,b1]=[-L,L],设置精度δ=1.计算初始观测点λ1和μ1为λ1=a1+0.382(b1-a1),μ1=a1+0.618(b1-a1),之后计算φ(λ1)和φ(μ1). 步骤2 比较函数值φ(λk)和φ(μk),如果φ(λk)>φ(μk),则转到步骤3;否则,转到步骤4. 步骤3 如果bk-λk≤δ,则转到步骤6;否则,设置ak+1:=λk,bk+1:=bk,λk+1:=μk,φ(λk+1):=φ(μk),μk+1:=αk+1+0.618(bk+1-ak+1)..计算φ(μk+1)并且转到步骤5. 步骤4 如果μk-αk≤δ,则转到步骤6;否则,设置ak+1:=ak,bk+1:=μk,μk+1:=λk,φ(μk+1):=φ(λk),λk+1:=ak+1+0.382(bk+1-ak+1).计算φ(λk+1)并且转到步骤5. 步骤5k:=k+1,转到步骤2. 算法2 所提混合算法框架. 步骤1 设定高斯核参数和惩罚因子区间,γ∈[2-L,2L],C∈[Cmin,Cmax].判断分类问题类别,如果是二分类问题,转到步骤2;n分类问题(n是大于2的正整数),转到步骤3. 步骤3n分类问题使用一对一策略[26],共有n(n-1)/2对二分类子问题,每一对i二分类问题,依次使用MGSA算法选择最优高斯核参数,记2ji,其中i=1,2,…,n(n-1)/2.设定高斯核参数缩小区间为[γmin,γmax]=[min{2ji},max{2ji}],并记[2jmin,2jmax],如果2jmin=2jmax,则设定[γmin,γmax]=[2jmin-1,2jmax+1].转到步骤4. 步骤4 在高斯核缩小区间[γmin,γmax]和惩罚因子区间[Cmin,Cmax],使用进化算法选择最优参数组合解. 步骤5 得到的最优参数组合训练SVM模型(多分类使用一对一策略[26]). 步骤6 使用训练好的SVM预测测试样本. 上述所提混合算法框架在阶段一采用了基于所证定理1提出的MGSA算法,相比于文献[11,20- 21]中广泛采用的ICDF-one-by-one方法,MGSA算法无需依次计算大量的ICDF值,降低了计算成本,能够快速搜索到候选集里最大ICDF值所对应的高斯核参数.所提混合算法框架在阶段二中可选择使用任何进化算法搜索最优参数组合.文献[21]结合SADE[22]算法优化SVM参数取得了较好的性能,记作ICDF-SADE.文中混合算法框架实验也采用该进化算法,记作MGSA-ICDF-SADE. SADE算法的自适应度函数选择SVM的性能测度函数.SVM性能测度函数选择k次交叉验证平均错分率,记作kCVMR,如式(18)所示: (18) 其中,MRi表示第i交叉验证错分率,根据文献[13,27]的建议,实验中采用5次交叉验证. 为验证算法的有效性,采用8个常用数据集进行测试实验.实验电脑平台配置G640 2.8 GHz CUP,4 GB RAM,window 7 32位系统,Matlab R2014a环境.实验使用的LIBSVM工具箱和数据集可在网站上下载[27],根据文献[12]建议,所有数据集都标准化到[-1,1].所有数据集随机选择70%作为训练样本,30%为测试样本.数据集基本特性如表1所示. 表1 数据集基本特性Table 1 Specifications of these datasets 根据文献[12]建议设定参数区间γ∈[2-20,220],C∈[2-7,27],这些区间足够覆盖具有很高泛化能力的SVM的参数组合. 文献[21]验证了ICDF-SADE法在SVM参数优化性能上比GS法和单独使用SADE[22]法效果好.为了突出所提算法的快速性,且能保持很好的性能,实验将比较MGSA-ICDF-SADE法与文献[21]中的ICDF-SADE法. SADE算法参数设置[21]:种群数NP=15,重组概率CR=0.9,自适应尺度因子变异参数F0=0.5,最大迭代次数GM=200,终止条件为达到最大迭代次数或者连续10次迭代的kCVMR值不变.依照文献[11,20- 21]将高斯核参数区间γ∈[2-20,220]离 散划分为候选集{2-20,2-19,…,220}. 为了验证所提混合算法中阶段一的MGSA算法的快速性,将该算法与ICDF-one-by-one进行比较,实验结果如表2所示. 表2 高斯核参数缩短区间及所需时间 Table 2 Shrunk interval of kernel parameter and the time cost 数据集核参数缩短区间所需时间/sICDF-oneby-oneMGSADiabetes[2-1,21]387.77123.29Heart[2-4,2-2]35.5110.32Ionosphere[2-4,2-2]148.6146.64Iris[2-1,21]8.732.76Wine[2-2,2-1]17.025.27Glass[20,25]37.6811.68Svmguide2[26,27]162.7249.15Vehicle[2-2,20]792.48250.98 从表2中结果可以看出,对所有数据集,文中根据定理1所提出的MGSA法确实搜索到与之前IC-DF-one-by-one法相同的高斯核参数缩短区间,但是在速度上大幅提高,原因在于减少了大量的候选核参数对距离函数ICDF的计算比较,使得搜索时间缩短至原来的约1/3. 为了验证所提混合算法框架的有效性,比较了所提MGSA-ICDF-SADE法与文献[21]中ICDF-SADE法进行SVM参数优化的训练时间和分类测试性能,实验结果如表3所示. 在表3中,对比了两种方法对每个数据集分别运行10次时的测试精度和训练时间的均值和方差,记录格式为:均值±方差.表3中结果表明,从各数据集的测试精度可看出所提方法很好地保持了搜索参数组合的SVM性能,但文中所提算法搜索SVM最优参数组合的训练时间比ICDF-SADE法大幅缩短. 表3 ICDF-SADE和MGSA-ICDF-SADE的测试精度和训练时间 图1给出了在数据集Iris上本文所提MGSA-ICDF-SADE法和ICDF-SADE[21]法的训练性能随时间变化的情况,图中两条线前段训练性能为零的部 图1 Iris上MGSA-ICDF-SADE与ICDF-SADE的训练性能随时间的变化 Fig.1 Training performance vs.time of ICDF-SADE and MGSA-ICDF-SADE on dataset Iris 分是算法通过ICDF计算选择最佳核参数区间的阶段(算法阶段一),可以看出所提算法比ICDF-SADE[21]大大缩短了在阶段一的计算时间,两者在后面阶段因采用了相同的进化算法(SADE)而训练性能相当,突出了所提算法对搜索SVM参数的快速性,且能保持很好的性能. 文中提出并证明了ICDF是高斯核参数的严格正单峰函数这一定理,并据此提出改进的黄金分割法(MGSA)来搜索候选集中的最好核参数,解决了当前研究中ICDF作为核参数选择指标需对候选集中大量候选参数依次计算造成的计算负担重、耗时长难题;然后提出一个基于MGSA和进化算法的快速SVM参数优化方法框架;最后通过比较实验验证了所提方法的有效性和快速性.结果表明所提方法具有较高的应用潜力. [1] VAPNIK V.The nature of statistical learning theory [M].New York:Springer Verlag,1995. [2] CHAPELLE O,HAFFNER P,VAPNIK V.Support vector machines for histogram-based image classification [J].IEEE Transactions on Neural Networks,1999,10(5):1055- 1064. [3] YU H,NI J.An improved ensemble learning method for classifying high-dimensional and imbalanced biomedicine data [J].IEEE/ACM Transactions on Computational Biology and Bioinformatics,2014,11 (4):657- 666. [4] LEOPOLD E,KINDERMANN J.Text categorization with support vector machines:how to represent texts in input space [J].Machine Learning,2002,46 (1/2/3):423- 444. [5] ZHANG X L,CHEN W,WANG B J.Intelligent fault diagnosis of rotating machinery using support vector machine with ant colony algorithm for synchronous feature selection and parameter optimization [J].Neurocomputing,2015,167:260- 279. [6] 邹文杰,王文静,杨付正.参考中性表情的人脸表情识别 [J].华南理工大学学报(自然科学版),2014,42(5):115- 121. ZOU Wen-jie,WANG Wen-jing,YANG Fu-zheng.Facial expression recognition referring to neutral expression [J].Journal of South China University of Technology (Natural Science Edition),2014,42(5):115- 121. [7] 牛海清,叶开发,许佳,等.基于粒子群优化支持向量机的电缆温度计算 [J].华南理工大学学报(自然科学版),2016,44(4):77- 83. NIU Hai-qing,YE Kai-fa,XU Jia,et al.Calculation of cable temperature based on support vector machine optimized by particle swarm algorithm [J].Journal of South China University of Technology(Natural Science Edition),2016,44(4):77- 83. [8] AYAT N E,CHERIET M,SUEN C Y.Automatic model selection for the optimization of SVM kernels [J].Pattern Recognition,2005,38(10):1733- 1745. [9] CHAPELLE O,VAPNIK V,BOUSQUET O,et al.Choosing multiple parameters for support vector machines [J].Machine Learning,2002,46 (1):131- 159. [10] KEERTHI S S,LIN C J.Asymptotic behaviors of support vector machines with Gaussian kernel [J].Neural Computation,2003,15(7):1667- 1689. [11] WU K P,WANG S D.Choosing the kernel parameters for support vector machines by the inter-cluster distance in the feature space [J].Pattern Recognition,2009,42(5):710- 717. [12] HSU C W,LIN C J.A comparison of methods for multiclass support vector machines [J].IEEE Transactions on Neural Networks,2002,13(2):415- 425. [13] KEERTHI S S,SINDHWANI V,CHAPELLE O.An efficient method for gradient-based adaptation of hyperparameters in SVM models [J].Advances in Neural Information Processing Systems,2007,19:673- 680. [14] DUAN K,KEERTHI S S,POO A N.Evaluation of simple performance measures for tuning SVM hyperparameters [J].Neurocomputing,2003,51:41- 59. [15] ADANKON M M,CHERIET M.Optimizing resources in model selection for support vector machine [J].Pattern Recognition,2007,40 (3):953- 963. [16] KEERTHI S S.Efficient tuning of SVM hyperparameters using radius/margin bound and iterative algorithms [J].IEEE Transactions on Neural Networks,2002,13(5):1225- 1229. [17] LIN S W,YING K C,CHEN S C,et al.Particle swarm optimization for parameter determination and feature selection of support vector machines [J].Expert Systems with Applications,2008,35(4):1817- 1824. [18] CHOU J S,CHENG M Y,WU Y W,et al.Optimizing parameters of support vector machine using fast messy genetic algorithm for dispute classification [J].Expert Systems with Applications,2014,41(8):3955- 3964. [19] ZHANG Y,ZHANG P.Machine training and parameter settings with sociale motional optimization algorithm for support vector machine [J].Pattern Recognition Letters,2015,54:36- 42. [20] BEZDEK C,PAL N R.Some new indexes of cluster validity [J].IEEE Transactions on Systems,Man,and Cybernetics,Part B (Cybernetics),1998,28 (3):301- 315. [21] ZHANG X,ZHOU J,WANG C,et al.Multi-class support vector machine optimized by inter-cluster distance and self-adaptive deferential evolution [J].Applied Mathematics and Computation,2012,218(9):4973- 4987. [22] 颜学峰,余娟,钱锋,等.基于改进差分进化算法的超临界水氧化动力学参数估计 [J].华东理工大学学报(自然科学版),2006,32 (1):94- 97. YAN Xue-feng,YU Juan,QIAN Feng,et al.Kinetic parameter estimation of oxidation in supercritical water based on modified differential evolution [J].Journal of East China University of Science and Technology (Natural Science Edition),2006,32 (1):94- 97. [23] FINE T.Optimum search for the location of the maximum of a unimodal function [J].IEEE Transactions on Information Theory,1966,12 (2):103- 111. [24] APOSTOL T M.Calculus (Second Edition) Vol.1:One-variable calculus with an introduction to linear algebra [M].Waltham:Cambridge University Press,1967. [25] SUN W Y,YUAN Y X.Optimization theory and methods:Nonlinear programming (Springer Optimization and Its Applications Vol.1) [M].New York:Springer,2006. [26] KREβEL U.Pairwise classification and support vector machines [C]∥ SCHÖLKOPF B,BURGES C J C,SMOLA A J.Advances in Kernel Methods-Support Vector Learning.Cambridge:MIT Press,1999:255- 268. [27] KAPP M N,SABOURIN R,MAUPIN P.A dynamic model selection strategy for support vector machine classifiers [J].Applied Soft Computing,2012,12 (8):2550- 2565. [28] CHANG C C,LIN C J.Libsvm:a library for support vector machines [EB/OL].(2015- 12- 14)[2016- 09- 03].https:∥www.csie.ntu.edu.tw/~cjlin/libsvm/, 2016. AnICDF-BasedFastParameterOptimizationApproachforSupportVectorMachines WANGJia-pengHUYue-mingLUOJia-xiang (School of Automation Science and Engineering, South China University of Technology, Guangzhou 510640, Guangdong, China) In the process of parameter optimization for support vector machines (SVMs) with Gaussian kernel, inter-cluster distance in feature spaces (ICDF) is an effective measure. However, ICDF may result in heavy computational load and large time consumption. In order to solve this problem, firstly, the theorem that ICDF is a positive strictly-unimodal function about Gaussian kernel parameter is proved. Then, according to this theorem, a modified golden section algorithm (MGSA) is proposed to search a shrunk value fast for kernel parameter in the candidate set. Thus, a fast parameter optimization approach on the basis of both MGSA and differential evolutionary algorithm is presented. Finally, some experiments are carried out to verify the effectiveness and rapidity of the proposed approach. support vector machine; inter-cluster distance; parameter optimization; kernel parameter; modified golden section algorithm 2016- 09- 07 国家科技重大专项(2014ZX02503-3);国家自然科学基金资助项目(61573146);华南理工大学中央高校基本科研业务费专项资金资助项目(2015zz0100) *Foundationitems: Supported by the National Science and Technology Major Project of the Ministry of Science and Technology of China(2014ZX02503-3) and the National Natural Science Foundation of China(61573146) 王加朋(1985-),男,博士生,主要从事模式识别、学习控制方向的研究.E-mail:fox007wjp@126.com †通信作者: 罗家祥(1979-),女,博士,副教授,主要从事优化调度、机器学习研究.E-mail:luojx@scut.edu.cn 1000- 565X(2017)07- 0135- 08 TP 18 10.3969/j.issn.1000-565X.2017.07.0191 相关基础
1.1 SVM及其参数优化问题
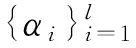

1.2 特征空间中的类间距离(ICDF)
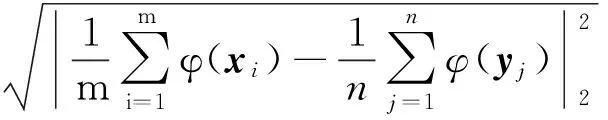


2 基于ICDF的SVM参数优化方法
2.1 ICDF的性质

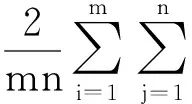




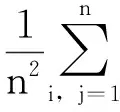

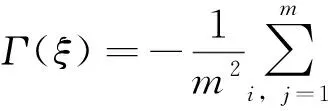

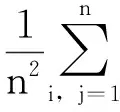






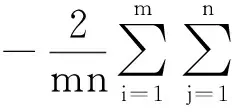

2.2 MGSA算法
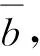

2.3 SVM参数优化混合算法框架

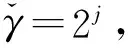
3 实验分析
3.1 实验参数设定

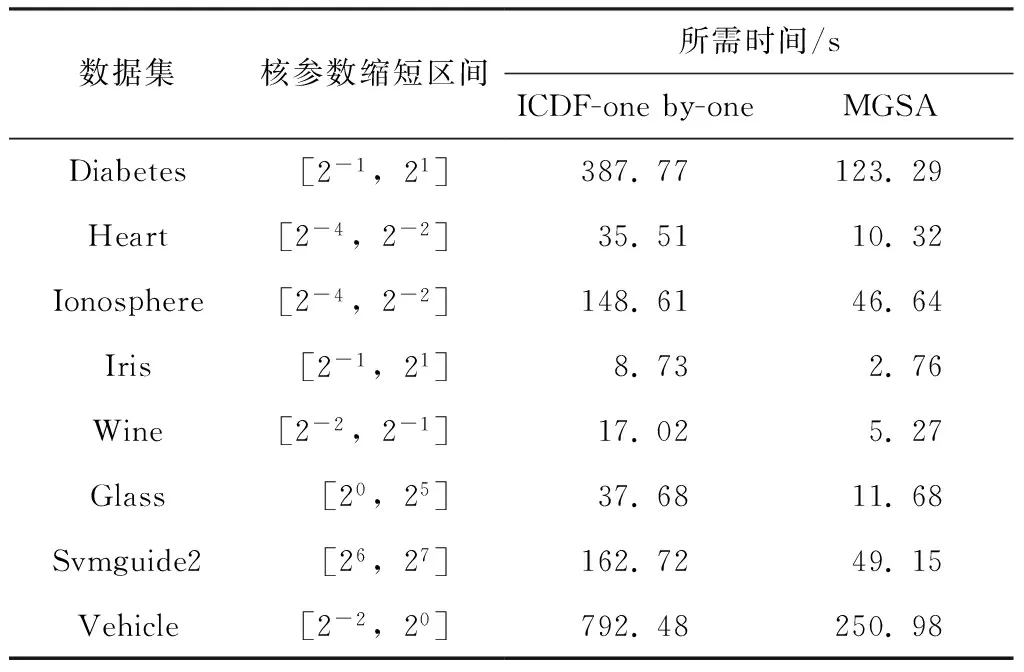
3.2 MGSA对核参数区间选择有效性验证
3.3 MGSA-ICDF-SADE的有效性验证

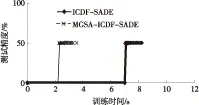
4 结语
