气隙放电电压的大气条件灰联度分析及预测*

牛海清 许佳 吴炬卓 余佳

(1.华南理工大学 电力学院， 广东 广州 510640； 2.珠海市供电局，广东 珠海 519000)

气隙放电电压的大气条件灰联度分析及预测*

牛海清1许佳1吴炬卓2余佳1

(1.华南理工大学 电力学院， 广东 广州 510640； 2.珠海市供电局，广东 珠海 519000)

为了研究大气条件参数对空气间隙放电电压的影响程度，使用放置在自然环境中的球-球电级全自动放电监测装置实时监测和记录的放电电压和大气条件参数数据，建立灰色关联度的计算模型，并通过计算得到各大气条件参数对放电电压的灰色关联度，结果表明，大气条件参数按灰色关联度大小(从大到小)的排序依次为气压、温度、风速、相对湿度、照度。以大气条件参数为输入，使用Chebyshev神经网络对放电电压进行预测，取得比BP神经网络更好的预测结果.根据大气条件参数的排序，分别取前两者(气压、温度)、前三者(气压、温度、风速)、前四者(气压、温度、风速、相对湿度)作为Chebyshev神经网络的输入，对放电电压进行预测.预测结果表明，随着输入个数的减少，预测的平均相对误差和最大相对误差变化很小.

大气条件；空气间隙；放电电压；灰色关联度；Chebyshev神经网络

空气间隙的放电特性是高压输变电外绝缘设计的重要依据.由放电理论可知，空气间隙放电电压受大气条件(气压、温度、湿度等)影响[1].针对大气条件参数对放电电压的影响，国内外进行了大量的试验研究[2- 6]，但多数试验是在实验室通过人工模拟试验条件完成的.从以往的研究可以看出，大气条件参数与放电电压的关系是多维、非线性的，所以采用传统数学统计方法难以建立精确的放电电压预测模型.

人工神经网络由于具有自学习、自组织、自适应等特点，广泛应用于非线性预测及推理.神经网络在电力系统中也取得了很好的应用效果[7- 11],但在电气设备外绝缘，特别是在空气间隙放电特性方面的应用研究还很缺乏.文献[5]以降雨强度、雨水电导率和温度为输入，以空气间隙击穿电压为输出，建立BP神经网络预测模型，并取得了较高的预测精度.文献[12]以气压、温度、相对湿度、风速和照度为输入，空气间隙放电电压为输出，建立复杂环境条件下空气间隙放电电压BP神经网络预测模型，其预测结果的平均相对误差仅为1.8 %.

针对大气条件参数对空气间隙放电电压的影响，本研究利用全自动放电装置，以在自然环境下监测记录到的空气间隙放电数据为依据，引入灰色关联度分析法研究了各大气条件参数对放电电压的影响，并对大气条件参数进行了灰色关联度排序；根据得到的灰色关联度排序，改变输入个数，分别建立Chebyshev神经网络预测模型对放电电压进行预测，以期为高压电气设备外绝缘的设计提供参考.

1 空气间隙放电电压和大气条件的监测

文中利用全自动放电监测装置，在广东某地区8个监测点实时监测大气条件参数和空气间隙的放电电压.

全自动放电监测装置每隔10 min以2 kV/s的速度[13]均匀升压直到空气间隙发生击穿放电，记录放电电压，同时采集每次放电时刻的气压、温度、风速、相对湿度和照度等大气条件参数.电压频率为50 Hz.放电监测装置于2011年1月开始投入运行，记录了8个监测点从2011年 1月至2011年9月的放电电压和大气条件参数数据.

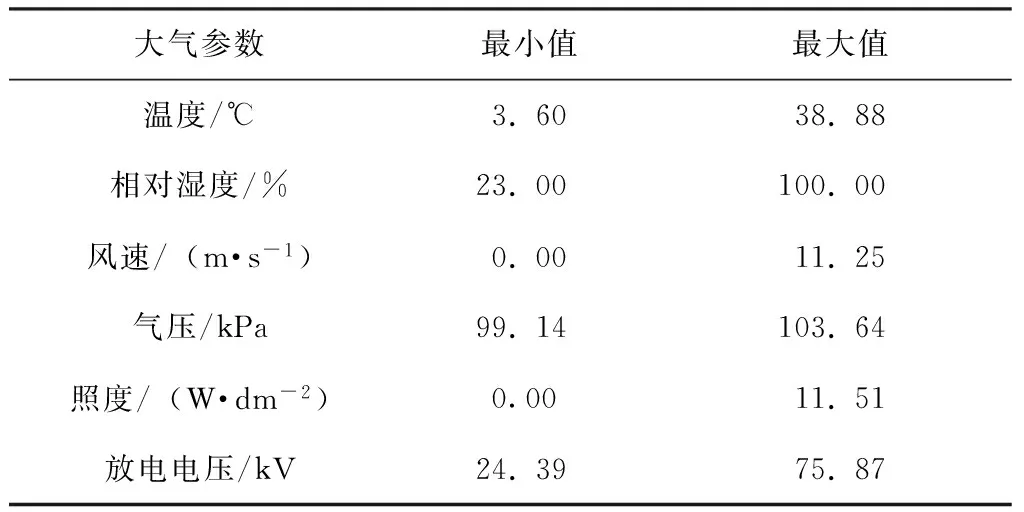
在监测时间段内，各参数变化范围如表1所示.由表1可见，温度、相对湿度、风速、照度和放电电压变化较大，气压变化较小.

表1 8个监测点各参数变化范围

Table 1 Range of all parameter variations of eight monitoring sites

大气参数最小值最大值温度/℃3.6038.88相对湿度/%23.00100.00风速/(m·s-1)0.0011.25气压/kPa99.14103.64照度/(W·dm-2)0.0011.51放电电压/kV24.3975.87

文献[12]根据监测数据，分别绘制了击穿电压随风速、温度、相对湿度、气压以及照度变化的散点图.分析可知，随着温度升高，间隙放电电压会略有降低，而且在气温越低的月份，降低的幅度会越明显；随着气压的升高，放电电压也会越高.

需要说明的是，由于本研究的监测数据均来自现场，故在分析单一参数与放电电压关系时无法排除其他参数的影响，而是通过统计大量数据使其呈现某种趋势.虽然相对湿度、风速、照度和放电电压的关系并未在散点图中反映，但并不意味着其和放电电压没有关系.为此，本研究采用灰色关联度分析法研究各大气条件参数对放电电压的影响程度.

2 大气条件参数影响程度的灰色关联度综合分析

由文献[14]可知，大气条件参数和放电电压监测数据符合“灰色系统”部分信息清楚、部分信息不清楚的特点，故可以使用灰色系统分析方法来分析大气条件参数对放电电压的影响.

2.1 灰色关联度分析法概述

灰色关联度分析法是灰色系统分析方法[15- 16]的一种，其核心是计算灰色关联度，以度量因素序列之间的关联程度.灰色关联度分析法的基本思想是根据因素序列相应曲线的几何形状的相似程度来判断其联系是否紧密，各曲线越接近，相应序列之间的关联度就越大，反之就越小.图1为灰色关联度分析示意图.图中序列1为参考序列，序列2、序列3和序列4为待比较序列.从图1中可以看出，序列2曲线的几何形状最接近序列1曲线的几何形状，其次为序列3曲线和序列4曲线，故对于参考序列1的关联度大小顺序为：序列2>序列3>序列4.

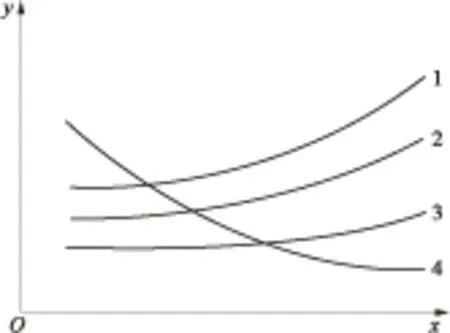
图1 灰色关联度分析示意图

2.2 灰色关联度计算模型

文中选择邓氏灰色关联度和斜率灰色关联度计算模型.

2.2.1 邓氏灰色关联度计算模型

邓氏灰色关联度计算模型是从相近性的角度反映序列之间的关联，主要考虑的是两个不同指标序列间距离的大小,计算步骤如下：

(1)确定参考序列以及待比较序列.其中参考序列X0代表目标行为序列，待比较序列Xi代表影响因素序列.

X0=[X0(1),X0(2),X0(3),…,X0(n)]

(1)

Xi=[Xi(1),Xi(2),Xi(3),…,Xi(n)]

(2)

式中，i=1,2,3,…,k，k表示影响因素的个数.

(2)对序列进行极性转换、初值化、规范化等环节处理，得到预处理后的参考序列和待比较序列x0和xi.

x0=[x0(1)，x0(2)，x0(3)，…，x0(n)]

(3)

xi=[xi(1)，xi(2)，xi(3)，…，xi(n)]

(4)

(3)求取差异信息序列和差异信息集，确定环境参数.差异信息序列Δi(n)定义为经预处理后的参考序列与待比较序列之差的绝对值.差异信息集Δ(n)定义为各影响因素差异信息序列的集合.

Δi(n)=|x0(n)-xi(n)|

(5)

Δ(n)=[Δ1，Δ2，Δ3，…，Δi]

(6)

环境参数定义为差异信息序列空间的两级差最大值与最小值.则可以得到环境参数如下：

(4)计算邓氏灰色关联系数和灰色关联度.

灰色关联系数：

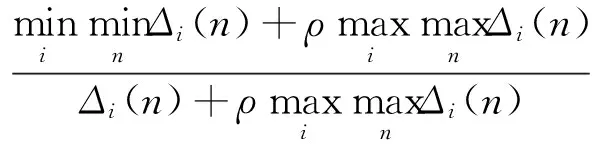
(7)

式中，ρ为分辨系数，其不同取值反映因素间不同的关系.分辨系数ρ的大小影响关联度的大小，但不会影响关联度的排序，其取值范围为[0,1]，文中取为0.5.

灰色关联度：

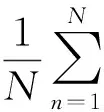
(8)

式中，N表示序列总长度.

2.2.2 斜率灰色关联度模型

斜率灰色关联度是基于相似性的角度反映序列之间的关联，主要考虑的是两个不同序列曲线的同一点处的变化率差异.

若X0(q)和Xi(q)为特征指标函数和相关指标函数，其中i=1,2,…,k，q=1，2，…m，则X0(q)和Xi(q)在q点处的灰色关联度系数ξi(q)为

ξi(q)=

(9)

其中，

(10)

Δxi(q)=xi(q+Δq)-xi(q)

(11)

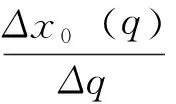
根据灰色关联系数，则可得到X0(q)和Xi(q)的斜率灰色关联度ξ0i，如下式所示：

(12)

2.2.3 灰色综合分析方法

设X0和Xi为长度相同，初值不等于0的指标序列，ξ0i和γ0i分别为指标序列X0和Xi的邓氏灰色关联度和斜率灰色关联度，则序列X0与Xi的综合灰色关联度ρ0i为

ρ0i=θξ0i+(1-θ)γ0i

(13)

式中，θ为权重系数，其取值范围为[0,1].当θ取值大时，更多考虑序列间相似程度，当θ取值小时，更多考虑序列变化速率的相似程度，文中θ取0.5.

灰色综合关联度能够较为全面地反映指标序列间的相似程度[17]，不仅体现了指标序列曲线在距离上的相近程度，而且体现了指标序列曲线在变化率上的相近程度.

2.3 大气条件参数对放电电压影响的灰色关联度分析

文中以#2监测点9个月的监测数据为分析样本，以放电电压为参考序列，以气压、温度、风速、相对湿度和照度为待比较序列，根据综合灰色关联度计算公式计算各大气参数对放电电压的综合灰色关联度，计算结果如表2所示.

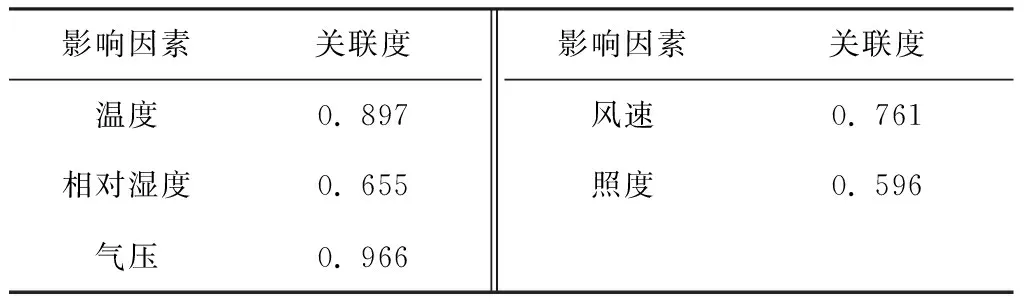
表2 综合灰色关联度计算结果Table 2 Comprehensive gray correlation results

从表2可以看出，气压对放电电压的灰色关联度最大，照度对放电电压的灰色关联度最小，说明气压对放电电压的影响最大，照度对放电电压的影响最小，各大气条件参数对放电电压的灰色关联度的排序为：气压>温度>风速>相对湿度>照度.

3 基于Chebyshev神经网络的放电电压预测

3.1 Chebyshev神经网络

Chebyshev神经网络是以Chebyshev正交多项式为激励函数的神经网络，具有结构简单、收敛速度快、计算精度高等特点[18- 20].图2为三层Chebyshev神经网络拓扑结构.

图中，P为输入向量，t为输出向量，wjs为输入层和隐含层的连接权值，cj为隐含层和输出层连接权值，则神经网络的数出t为

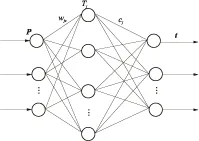
图2 Chebyshev神经网络拓扑结构

(14)

式中，g为输入向量的维数，Tj(x)为Chebyshev正交多项式，其表达形式如下：

T1(x)=1

T2(x)=x

⋮

Tj(x)=2xTj-1(x)-Tj-2(x)

(15)

式中，j=3,4,…,f，f为Chebyshev正交多项式的阶数.

设期望输出为sd(d=1,2，…,l)，并令神经网络的误差为

(16)

则可以按下式对神经网络权值进行修正：

(17)

式中，η为学习步长，Δcr和Δwjs可以通过求偏导得到.

(18)

3.2 放电电压预测

为消除各参数量纲的影响，并使样本数据更适合于神经网络处理，需对各参数进行归一化，如式(19)所示:

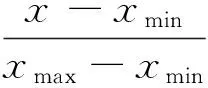
(19)

式中，xmax和xmin分别为各参数的最大值和最小值.x和X分别为归一化之前和之后的样本值.

从#1监测点9个月的监测数据中随机挑选4 800组作为训练样本，210组作为检验样本.以大气条件参数气压、温度、风速、相对湿度和照度作为网络的输入，以放电电压作为网络的输出.学习步长设定为8×10-3，误差精度设为0.001，最大训练次数为50 000次.预测结果为：最大相对误差7.01 %、最小相对误差0、平均相对误差1.62 %.

#1监测点检验样本预测值与实际值的对比图如图3所示.从图中可以看出，使用Chebyshev神经网络能够准确对放电电压进行预测.

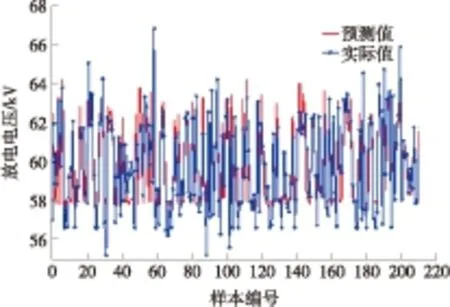
图3 #1监测点检验样本预测值与实际值的对比图

Fig.3 Comparison chart between predicted value and the actual value or #1 monitoring points test sample

为检验利用#1监测点样本训练好的神经网络是否适用于其他监测点，分别从#2-#8共7个监测点随机挑选200组数据对训练好的网络进行检验，结果如表3所示.

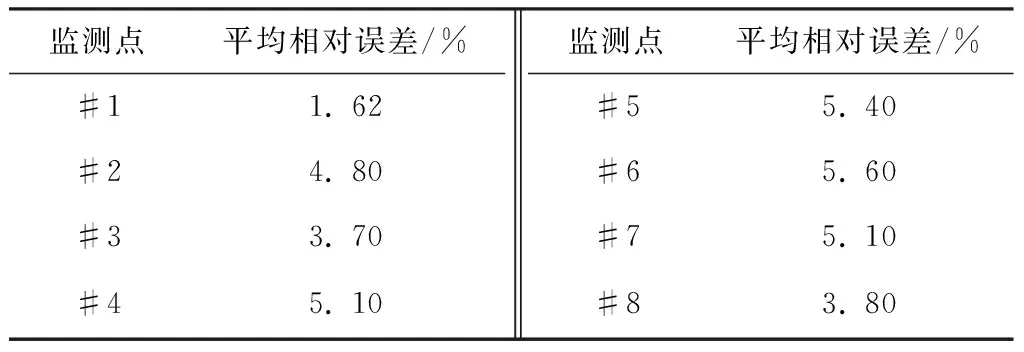
表3 各监测点检验样本的预测结果Table 3 Predict results of the monitoring points test samples

从表3可以看出，使用#1监测点样本数据训练好的神经网络预测其他监测点的放电电压时，误差有所升高，但仍在工程误差范围内.

3.3 两种神经网络预测结果对比

在使用BP神经网络对放电电压进行预测时，同样以大气条件参数气压、温度、风速、相对湿度和照度作为网络的输入，以放电电压作为网络的输出，网络结构根据文献[12]选为5- 35- 35- 1，误差精度同样设为0.001，学习效率设为0.05，最大训练次数为5 000.使用#1监测点同样的训练样本和检验样本分别对网络进行训练和检验，对比使用Chebyshev神经网络的收敛时间和预测误差，结果如表4所示.

表4 BP神经网络和Chebyshev神经网络性能对比图

Table 4 Comparison chart of BP neural network and Chebyshev neural network performance

网络类型收敛时间/s预测平均相对误差/%BP神经网络42002.38Chebyshev神经网络301.62

从表4可以看出，对放电电压进行预测时，相比于使用BP神经网络，使用Chebyshev神经网络在取得更高预测精度的同时，大大降低了网络训练过程的收敛时间.

3.4 不同输入条件的预测结果分析

为进一步研究大气条件参数对放电电压预测精度的影响，文中根据各大气条件参数的灰色关联度排序，分别取气压、温度、风速、相对湿度、照度为输入(输入1)，气压、温度、风速、相对湿度为输入(输入2)，气压、温度、风速为输入(输入3)，气压、温度为输入(输入4)，并结合Chebyshev神经网络对放电电压进行预测，预测使用的样本同样为#1监测点样本数据，预测结果如表5所示.

表5 不同输入对应的预测结果Table 5 Prediction results corresponding to different inputs

从表5可以看出，随着网络输入个数的减少，放电电压预测结果的平均相对误差和最大相对误差改变很小.特别地，当输入个数变为2时，平均相对误差和最大相对误差分别为1.63 %、7.62 %，而输入个数为5个时的平均相对误差和最大相对误差分别为1.62 %、7.01 %，两者的误差基本没有变化.这也间接证明了在各大气条件参数中，气压和温度是影响放电电压的主要因素.

4 结论

本研究基于全自动放电监测装置在广东某地区8个监测点的监测数据，引入灰色关联度分析法研究各大气条件参数对放电电压的影响，并提出使用Chebyshev神经网络对放电电压进行预测，得到以下结论:

(1)灰色关联度综合体现了指标序列曲线在距离和变化率上的相近程度，能够全面分析各大气条件参数对放电电压的影响.通过计算各大气条件参数对放电电压的灰色关联度，得到各大气条件参数的关联度排序为：气压>温度>风速>相对湿度>照度，即气压对放电电压影响最大，照度对放电电压影响最小.

(2)本研究提出使用Chebyshev神经网络预测放电电压，在不考虑凝露状态情况下，预测结果的平均相对误差为1.78%；使用1#监测点样本数据训练好的神经网络预测其他监测点的放电电压时，误差有所升高，但仍在工程误差范围内.

(3)与BP神经网络相比，使用Chebyshev神经网络对放电电压进行预测时，能够在取得更高预测精度的同时，大大降低网络训练过程的收敛时间.

(4)根据大气条件参数关联度排序改变网络输入个数预测放电电压时，随着网络输入个数的减少，放电电压预测结果的平均相对误差和最大相对误差变化很小.

[1] 孙才新，司马文霞，舒立春，等.大气环境与电气外绝缘 [M].北京：中国电力出版社，2002.

[2] 徐勇，汪霄飞，朱英浩.大气条件对空气间隙放电特性的影响及其数值解析式 [J].电工技术学报，2007， 22(4)：21- 26.

XU Yong,WANG Xiao-fei,ZHU Ying-hao.Effect of air gap discharge characteristics of atmospheric conditions and numerical analysis formula [J].Transactions of China Electrotechnical Society,2007,22 (4):21- 26.

[3] 卞星明，惠建峰，黄海鲲，等.气压和湿度对正直流电晕流注脉冲特性的影响 [J].高电压技术，2009，35(10)：2371- 2375.

BIAN Xing-ming,HUI Jian-feng,HUANG Hai-kun,et al.Influence of air pressure and humidity on positive DC corona streamer pulse characteristics [J].High Voltage Engineering,2009,35 (10):2371- 2375.

[4] 蒋兴良，赵智亮，孙才新，等.低气压正棒-板短间隙操作冲击放电特性 [J].高电压技术，2002，28(7)：7- 9.

JIANG Xing-liang,ZHAO Zhi-liang,SUN Cai-xin,et al Switching impulse discharge performance and voltage correction for positive rod-plane short air gaps in low air-pre-ssure [J].High Voltage Engineering,2002,28 (7):7- 9.

[5] 袁耀，蒋兴良，杜勇，等.应用人工神经网络预测棒-板短空气间隙在淋雨条件下的交流放电电压 [J] .高电压技术,2012，38(1)：102- 108.

YUAN Yao,JIANG Xing-liang,DU Yong,et al.Predictions of the AC discharge voltage of short rod-plane air gap under rain conditions with the application of ANN [J].High Voltage Engineering,2012,38 (1):102- 108 .

[6] 蒋兴良，刘伟，奚思建，等.降雨对“棒-板”短空气间隙正极性直流放电特性的影响 [J].高电压技术，2011，37(2)：261- 267.

JIANG Xing-liang,LIU Wei,XI Si-jian,et al.Influence of rain on positive DC discharge characteristicof rod-plane short air gap [J].High Voltage Engineering,2011,37 (2):261- 267.

[7] 李练兵，张秀云，王志华，等.故障树和BAM神经网络在光伏并网故障诊断中的应用 [J].电工技术学报，2015，30(2)：248- 254.

LI Lian-bing,ZHANG Xiu-yun,WANG Zhi-hua,et al.Fault diagnosis in solar photovoltaic grid-connected power system based on fault tree and BAM neural network [J].Transactions of China Electrotechnical Society,2015,30 (2):248- 254.

[8] 王贺，胡志坚，陈珍，等.基于集合经验模态分解和小波神经网络的短期风功率组合预测 [J].电工技术学报，2013,28(9)：137- 144.

WANG He,HU Zhi-jian,CHEN Zhen,et al.A hybrid model for wind power forecasting based on ensemble empirical mode decomposition and wavelet neural networks [J].Transactions of China Electrotechnical Society,2013,28 (9):137- 144.

[9] 修春波，任晓，李艳晴，等.基于卡尔曼滤波的风速序列短期预测方法 [J].电工技术学报，2014,29(2)：253- 259.

XIU Chun-bo,REN Xiao,LI Yan-qing,et al.Short-term prediction method of wind speed series based on kalmanfiltering fusion [J].Transactions of China Electrotechnical Society,2014,29(2):253- 259.

[10] 何耀耀,许启发,杨善林,等.基于RBF神经网络分位数回归的电力负荷概率密度预测方法 [J].中国电机工程学报,2013,33(1):93- 98.

HE Yao-yao,XU Qi-fa,YANG Shan-lin,et al.A power load probability density forecasting method based on RBF neural network quantile regression [J].Proceedings of the CSEE,2013,33(1):93- 98.

[11] 肖建平,李生虎,吴可汗,等.一种新的基于神经网络的电力系统谐波检测方法研究 [J].电工技术学报,

2013,28(S2):345- 348，371.

XIAO Jian-ping ,LI Sheng-hu,WU Ke-han,et al.A novel approach of harmonic detection in power system based on neural network [J].Transactions of China Electrotechnical Society,2013,28(S2):345- 348，371.

[12] 张耿斌，罗新，沈杨杨，等.大气条件对气隙放电电压的影响及神经网络在放电电压预测中的应用 [J].高电压技术，2014,40(2)：564- 571.

ZHANG Geng-bin,LUO Xin,SHEN Yang-yang,et al.Effect of atmosphere condition on discharge characteristics of air gap and the application of neural network [J].High Voltage Engineering,2014,40 (2):564- 571.

[13] GB 311.6—1983,高电压试验技术 [S].

[14] 林浩然.基于多元统计分析的大气参数对空气间隙外绝缘影响的试验研究 [D].广州：华南理工大学，2012.

[15] 邓聚龙，灰色系统理论教程 [M].武汉：华中理工大学出版社，1990.

[16] 邓聚龙，灰理论基础 [M].武汉：华中理工大学出版社，2002.

[17] 阳林，郝艳捧，黎卫国.等.输电线路覆冰与导线温度和微气象参数关联分析 [J].高电压技术，2010,36(3)：775- 781.

YANG Lin,HAO Yan-peng,LI Wei-guo,et al.Relationships among transmission line icing conductor temperature and local meteorology using grey relational analysis [J].High Voltage Engineering,2010,36 (3):775- 781.

[18] 杨胡萍，王承飞，朱开成.基于相空间重构和Chebyshev正交基神经网络的短期负荷预测 [J].电力系统保护与控制，2012,40(24)：95- 99.

YANG Hu-ping,WANG Cheng-fei,ZHU Kai-cheng.Short-term load forecasting based on phase space reconstruction and Chebyshev orthogonal basis neural network [J].Power System Protection and Control,2012,40(24)：95- 99.

[19] 张雨浓，李巍，蔡炳煌，等.切比雪夫正交基神经网络的权值直接确定法 [J].计算机仿真，2009,26(1)：157- 161.

ZHANG Yu-nong,LI Wei,CAI Bing-huang,et al.A chebyshev orthogonal basis neural network with direct weight determintion [J].Computer Simulation,2009,26(1)：157- 161.

[20] 邹阿金,沈建中.基于Chebyshev神经网络的非线性预测应用研究 [J].计算机应用,2001(4):14- 15.

ZOU A-jin,SHEN Jian-zhong.The nonlinear prediction study based on Chebyshev neural networks [J].Compu-ter Applications,2001(4):14- 15.

GrayCorrelationAnalysisofAtmosphericConditionsandPredictionofAirGapDischargeVoltage

NIUHai-qing1XUJia1WUJu-zhuo2YUJia1

(1. School of Electric Power,South China University of Technology,Guangzhou 510640,Guangdong,China; 2. Zhuhai Power Supply Bureau,Zhuhai 519000,Guangdong,China)

In order to discover the impact of atmospheric condition parameters on air gap discharge voltage,a automatic discharge monitoring device with ball-ball electrode was used to monitor and record the discharge voltage and atmospheric condition parameters in natural environment,and a calculation model of gray correlation was established,by which the gray correlations between atmospheric condition parameters and discharge voltage were obtained,finding that the gray correlations of atmospheric condition parameters are indicative of the following order: pressure>temperature>wind speed>relative humidity>illumination. Then,by taking the atmospheric condition parameters as inputs,Chebyshev neural network was used to predict the discharge voltage,with better prediction results being obtained in comparison with BP neural network. Finally,according to the sort of atmospheric condition parameters,the first two (pressure and temperature),the first three (pressure,temperature and wind speed) and the first four (pressure,temperature,wind speed and relative humidity) parameters were respectively taken as the inputs of Chebyshev neural network to predict the discharge voltage. The results show that,with the reduction of the number of inputs,the average relative error and maximum relative error of the predicted values both have little change.

atmospheric condition;air gap;discharge voltage;gray correlation;Chebyshev neural network

2016- 06- 23

国家高技术研究发展计划(863计划)项目(2015AA050201)

*Foundationitem: Supported by the National High-tech R&D Program of China(863 Program) (2015AA050201)

牛海清(1969-)，女，博士，副教授，主要从事高压输电线路及高压电气设备相关问题的研究.E-mail：niuhq@scut.edu.cn

1000- 565X(2017)07- 0048- 07

TM 83

10.3969/j.issn.1000- 565X.2017.07.007