赋值法求系数和

福建 蔡爱兵

赋值法求系数和

福建 蔡爱兵

二项式定理为高考的必考考点，常见题型为选择题、填空题，以计算某一项的系数或者某几项系数之和为主，主要是考查二项式定理和赋值法，一般是基础题或者中档题，在备考复习时，要侧重基础.本文结合最近几年高考试题中考查二项式定理的部分，主要探讨赋值法求系数和.

一、针对特定一项的1赋值法

( )

A.-1 B.0

C.1 D. 2

【评注】考查对二项式定理和二项展开式的性质，重点考查实践意识和创新能力，体现正难则反.

【例2】(2012·浙江理·第14题)若将函数f(x)=x5表示为f(x)=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5，其中a0,a1,a2，…,a5为实数，则a3=________.

【解析】法一：应用二项展开式，等式两边对应项系数相等.

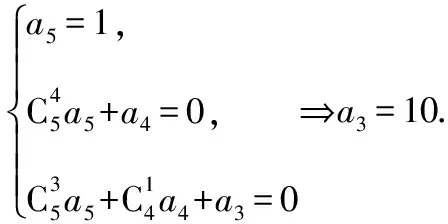
法二：对等式f(x)=x5=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5两边连续对x求导三次得60x2=6a3+24a4(1+x)+60a5(1+x)2，再运用赋值法，令x=-1得60=6a3，即a3=10.

【评注】求某项系数，先求导数，把要求的项系数变为常数项，在赋值，只留下常数项，事半功倍.

二、针对奇偶项的-1，1赋值法

【例3】(2015·全国新课标Ⅱ理·第15题)(a+x)(1+x)4的展开式中x的奇数次幂项的系数之和为32，则a=________.

【解析】法一：应用二项展开式，(1+x)4=1+4x+6x2+4x3+x4，故(a+x)(1+x)4的展开式中x的奇数次幂项分别为4ax,4ax3,x,6x3,x5，其系数之和为4a+4a+1+6+1=32，解得a=3.

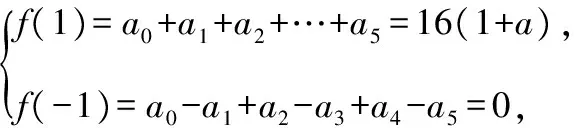
【评注】本题考查二项式定理，准确写出二项展开式，能正确求出奇数次幂项以及相应的系数和，从而列方程求参数值，属于中档题.

( )

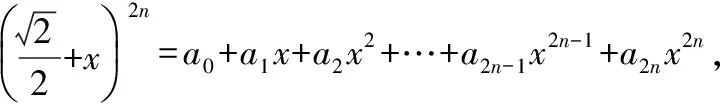
A.-1 B.0

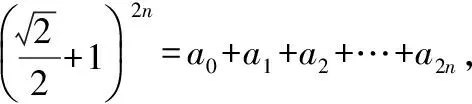
【评注】本题主要是考查二项式定理奇偶项系数，直接计算比较繁琐，先变形再赋值，则相对简单.

三、针对所有项的1赋值法

( )

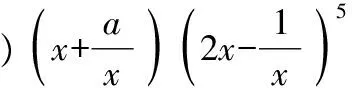
A.-40 B.-20

C.20 D.40

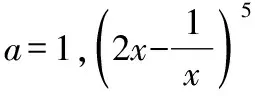
【评注】本题关键在于各项系数之和的赋值计算，求出a，再应用二项式展开式，计算常数项.

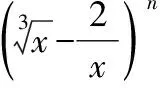
福建省漳州市台商投资区厦门双十中学漳州校区)