中国城市人口规模的空间演化及影响因素
2017-12-11吴友刘乃全
吴友+++刘乃全

摘要:从集聚收益与成本角度探讨城市人口规模的空间演化机制,并采用含有地理距离、经济距离和流动网络权重的空间自回归模型,实证检验不同层级城市人口规模的空间演化路径与影响因素。研究发现不同层级城市人口规模演化路径均表现出显著的收敛增长特性,且1类大及以上城市的收敛增长系数最大,2类大城市和小城市系数大小相当并居中,中等城市的系数最小;工资、第三产业发展、教育、医疗水平是促进人口规模增长的主要收益因素,环境污染强度是抑制人口规模增长的主要成本因素。
关键词:人口规模;空间演化;集聚收益;集聚成本;收敛增长
中图分类号:F293;C922文献标识码:A文章编号:1000-4149(2017)06-0032-11
DOI:103969/jissn1000-4149201706004
收稿日期:2016-10-25;
修订日期:2017-02-23
基金项目:国家社会科学基金年度项目“长三角城市群人口空间分布优化研究”(15BRK025)。
作者简介:吴友,上海财经大学城市与区域科学学院/财经研究所博士研究生;刘乃全,上海财经大学城市与区域科学学院/财经研究所研究员,博士生导师。
The Spatial Evolution and Influence Factors of Urban Population:
Empirical Analysis on 264 Cities Data in China
WU You,LIU Naiquan
(Institute of Finance and Economics Research/School of Urban and Regional Science,
Shanghai University of Finance and Economics, Shanghai 200433, China)
Abstract:From the perspective of agglomeration benefits and costs, this paper theoretically discusses the mechanism of the spatial evolution path of the urban population size, and then empirically analyses the spatial evolution paths of population size among different levels of cities, considering the spatial correlation among cities and using various space regression methods which respectively contain three spatial weight matrixesgeographic distance, economic gap and social network. We can draw the following conclusions: All cities showed significant spatial convergence growth, but with different convergence coefficients. The huge cities own the highest coefficient, big cities and small cities owe the second one and the medium cities owe the lowest. Wage, the third industry development, educational development and medical development are the main benefit factors for promoting population growth, and environmental pollution intensity is main cost factor to inhibit the growth of population size.
Keywords:population size; spatial evolution; agglomeration benefits; agglomeration costs; convergence growth
《人口與经济》2017年第6期
吴友,等:中国城市人口规模的空间演化及影响因素
一、引言
随着我国改革开放的不断深入以及城镇化进程的快速推进,我国的城市人口规模演化呈现出新的态势。一方面,受城乡分割的户籍制度影响,就业于大城市的外来人口未能在教育、就业、医疗、养老、保障性住房等方面享受本地居民的基本公共服务,生活成本不断上升。此外,大城市空间无序开发、人口过度集聚,交通拥堵问题严重,环境污染加剧,城市问题不断突出,一些流动人口不再青睐大城市的就业与生活,引致大城市的人口规模增长速度逐渐放缓。另一方面,我国中小城市的基础设施逐步升级,公共服务水平不断提高,教育事业快速发展,城市吸引人口集聚水平迅速增强。此外,中小城市顺应产业发展规律,积极承接东部沿海大城市的产业转移,就业机会明显增加,一些外出劳动力纷纷回流就业与发展,小城市的人口规模减速逐渐放缓。那么,我国现阶段城市人口分布具有什么样的特征?不同规模的城市人口演化路径又有怎样的区别?
上述现象与问题得到了党和国家领导高层以及学者的密切关注,国务院2014年公布的《国家新型城镇化规划(2014—2020年)》中指出,目前,我国的城镇空间分布和规模结构不合理,与资源环境承载能力不匹配;城市管理服务水平不高,“城市病”问题日益突出。规划强调,我们要优化城镇化布局和形态,促进各类城市协调发展,共同推进中心城市辐射带动功能与中小城市快速发展。因此,在中国区域发展极不平衡的现状下,人口规模不同的城市应该遵循什么样的发展路径,成为城市问题研究者所关注的热点。城市人口规模演化多表现为收敛增长、发散增长和平行增长三种主要路径[1]。其中,收敛增长表现为:随着城市的发展,集聚收益的增加小于拥挤效应的增加,使得距离城市稳态规模越近的城市(如大城市),人口增长速度越慢。发散增长表现为:距离城市稳态规模越近的城市,人口增长速度越快。平行增长表现为:所有城市人口规模均以相同的速度朝其稳态值发展。学者纷纷利用不同的样本对城市人口规模演变路径进行了实证研究,但结果并没有达成一致意见。一部分学者以美国城市为样本,认为城市人口规模的演变以收敛增长方式趋于稳态,进一步通过细分时间段发现,在1970—2000年间,只有人口大于5万人的郡县样本人口规模表现出收敛增长趋势明显;而将样本时间段缩短在1980—2000年间,所有美国城市样本的人口规模均表现出显著的收敛增长趋势[2-3]。同样以中国城市为样本的研究,也发现中国城市增长呈现收敛增长趋势[4-7]。此外,一部分学者的研究结果则显示,城市人口规模演化遵循发散增长路径。如发现巴西和印度大城市的人口增长速度均快于小城市;中国在20世纪80年代中等城市与小城市之间均呈现发散增长[8-9]。同时,部分学者以法国、日本、美国、中国的城市为研究对象,发现在长期内,这些国家城市人口规模演化均以平行增长方式趋于各自稳态[1,10-13]。endprint
相比于国外学者对演化路径的探讨,国内学者更多将城市作为一个孤立个体,通过城市内部收益与成本角度来测度城市最优规模[14-16]。但是,不同城市之间有着密切的联系,人口规模演化具有联动效应,因此割裂地分析某单个城市人口最优规模以及人口规模的演变难免会出现误差,并且国内学者在测度我国城市人口规模时多以省份作为考察单位、以年末总人口作为考察数据样本,一定程度上加大了测度城市人口规模增长的偏误。此外,在进行经验分析时,大多考察本区域发展要素对自身人口规模增长的影响,并未考虑相邻区域发展要素对本区域人口规模增长的影响,在中国人口大量转移的背景下,忽视要素之间的空间联动性,将大大降低研究结论的可信度。基于此,本文首先从理论上探讨了城市人口规模空间演化机制,并以中国264个地级及以上城市“五普”和“六普”中常住人口数据为样本,分别以城市之间地理距离、经济距离和流动网络作为空间权重矩阵,运用空间自回归模型(SAC),检验我国城市人口规模的演化路径,并进一步测度不同层级样本城市人口规模演化特性。
二、城市人口规模空间演化的理论分析
城市的最优规模取决于城市功能定位以及资源集聚,如较高的工资水平、充足的就业岗位、完善的医疗与教育体系等基础设施,这些优质资源引起城市人口规模进一步扩张的同时,也为城市带来较大的集聚成本,如城市交通拥挤、地租攀升、污染严重等[17](见图1)。基于以上分析,本文通过构建城市人口均衡规模的微观模型,探讨城市人口规模空间演化机制。假定存在一个城市,给定城市中心(CBD),所有的产品生产集中于CBD,代表性工人居住在CBD以外、城市边界之内,每天支付通勤成本赶往CBD上班。给定代表性消费者的效用为U(M,S),其中M表示复合商品的数量,S表示消费的土地数量,且U/M>0和U/S>0,城市土地与代表性消费者均假设为同质的。为简化模型,将复合商品的价格指数恒定为1,在给定收入Y时,居住在距离CBD r处的消费者的预算线为M+R(r)S=Y-T(r)-P(r),其中R(r)表示在r处的地租,T(r)表示从r处到CBD的通勤成本,P(r)表示在r处处理污染的成本,且满足R′(r)<0、P′(r)<0、T′(r)>0、limr→rfP(r)=0以及limr→0T(r)=0,limr→∞T(r)=∞。
在每一个r处,消费者在预算约束下,为使其效用最大,会选择对应的M和S,记为
M^
[Y-T(r)-P(r),R(r)]和S^[Y-T(r)-P(r),R(r)],因此,我们可知,消费者的间接效用为:V[Y-T(r)-P(r),R(r)]=U{M^[Y-T(r)-P(r),R(r)],S^[Y-T(r)-P(r),R(r)]},其中,Y-T(r)-P(r)为可支配收入。在单个城市达到均衡时,每个消费者必定会达到同样的效用U—,这样才使其余消费者没有改变r的动机,则我们可定义为:V[Y-T(r)-P(r),R(r)]=U—,且r≤rf。 rf为城市边界,R(rf)=Rc>0,在边界处的租金为城市土地的机会成本。假设效用U—外生,我们可以求出每个家庭在可支配收入约束下的竞租函数,R(r)=φ[Y-T(r)-P(r),U—],在城市边界处,我们可以求出Rc=φ[Y-T(rf),U—],对应的稳定均衡城市边界rf(Y,U—),均衡的商品数量和土地消费数量,如以下公式所示:
Me[Y-T(r)-P(r),U—]=M^{Y-T(r)-P(r),φ[Y-T(r),U—]}(1)
Se[Y-T(r)-P(r),U—]=S^{Y-T(r)-P(r),φ[Y-T(r)-P(r),U—]}(2)
接下來,假定在r处的可供消费的土地总数量为D(r),则均衡时在r处的总人口为D(r)/Se[Y-T(r)-P(r),U—],因此,给定(Y,U—),城市的均衡总人口Ne(Y,U—)如下式所示:
Ne(Y,U—)=∫rf(Y,U—)0D(r)/Se[Y-T(r)-P(r),U—]dr(3)
通过上述分析,我们同样可以从式(3)中反解出Y(U—,N),并定义为代表性消费者的收入函数,且Y(U—,N)/U—>0,Y(U—,N)/N>0,Y2(U—,N)/N2<0,表明人口规模越大,代表性消费者获得的集聚收益越高,边际集聚收益越低,如图2中的Y曲线。
由于前面假定一个城市的土地与代表性消费者均为同质的,我们可以求出代表性消费者的成本函数,为:C(U—,N)=M[Y-T(r),U—]+T(r)+P(r)+R(r)S[Y-T(r),U—],式中,第一项为r处代表性消费者对复合性商品的消费,第二项为r处代表性消费者的通勤成本,第三项为r处代表性消费者的污染成本,第四项为r处代表性消费者的土地消费,且C(U—,N)/U—>0,C(U—,N)/N>0,C2(U—,N)/N2>0, 表明人口规模越大,代表性消费者获得拥挤成本也越高,边际集聚成本越高,如图2中的C曲线。
最后,根据代表性消费者的收入函数Y(U—,N)和成本函数C(U—,N),我们可以求出一个城市代表性消费者的总收益函数:TB=Y(U—,N)-C(U—,N)。城市达到均衡时,TB=0,即 Y*(U—,N*)=C*(U—,N*)。
从均衡式中,我们可以得出以下结论:给定城市效应水平,均衡的城市人口规模是集聚收益与集聚成本权衡的结果[18-22];给定城市效应水平,城市人口规模内生影响收益与成本函数,如图2所示。
通过上述分析发现,必定存在一个最优城市人口规模N0,使城市总效用达到最大,表达式为:Umax=Max{UY(U,N0)=C(U,N0),N0>0},可以推断,城市效应与城市人口是倒“U”型关系[18,20]。同时,我们可以发现,最优城市规模并不代表均衡的城市规模,因为社会总成本并不完全由代表性消费者承担,相当一部分由政府分摊,因此,城市人口规模的稳态均衡点必定高于其最优规模[15]。当城市给定效用U1
从理论模型推导中,我们得出城市人口规模演化是集聚收益与集聚成本相互权衡的结果(见图2),且在人口可自由流动前提下,城市人口规模最终朝其稳态均衡点演化(见图3),依此,将t期城市的稳态均衡人口规模表达式定义为N*t=g(Yt,Ct,N—*)。其中,N*t由t期的城市集聚收益Yt、集聚成本Ct以及城市初始人口规模非稳态均衡N—*共同决定。为使计量模型具体化,我们将模型设定为CD函数形式,表达式为N*t=BYtCβt(N—*)γ,两边取对数为:lnN*t=lnB+αlnYt+βlnCt+γlnN—*,则城市人口规模从非稳态均衡至稳态均衡演化路径表达式为:
g·t=ln(N*t/N—*)=lnB+αlnYt+βlnCt+(γ-1)lnN—*(4)
式中,α大于0,集聚收益正向影响城市人口规模朝其稳态均衡演化;β小于0,集聚成本则抑制城市人口规模朝其稳态规模演化;如果γ-1显著大于0,则说明城市人口规模演化路径表现为发散增长,γ-1显著小于0,则说明城市人口规模演化路径表现为收敛增长,γ-1不显著,则说明城市人口规模演化路径表现为平行增长。
三、城市人口规模空间演化的研究设计
1中国城市人口规模层级划分与空间分布
(1)中国城市人口规模的层级划分。本文根据国务院2014年颁布的《关于调整城市规模划分标准的通知》,将城市按照城区常住人口分为7个档,超大城市、特大城市、1类大城市、2类大城市、中等城市、1类小城市和2类小城市。作者根据“五普”和“六普”公布的城市市区和城市郊区常住人口数据,测算出城区的常住人口数据。由于2类小城市的样本数据缺失严重,因此,本文将2类小城市与1类小城
市
合并为小城市,形成6类城市,最终样本选择为264个地级及以上城市。按照“六普”数据计算,其中,城区常住人口大于1000万的超大城市有北京、天津、上海、广州、深圳和重庆;城区常住人口在500万—1000万之间的特大城市有10个。此外,1类大城市有21个、2类大城市有99个,中等城市有96个,小城市32个,如图4所示。
(2)中国城市人口规模的空间分布。以我国264个地级及以上城市2000和2010年的城区常住人口数据为样本,从其空间分布图(见图5)中,我们可以看出,分析样本的总人口在2000和2010年分别占全国的比例为8699%和8801%,样本选择具有一定代表性。图5中白色区域为自治州和县级市,没有纳入我们的分析样本中。从全国范围看,我国将近80%的人口分布在中国版图的东南部,人口区域分布严重不均衡。
对比2000年城区常住人口的空间分布图,从2010年的分布图中,我们可以看出人口在1000万以上的超大城市增加了重庆、广州、天津、深圳,表现为6个超大城市样本;城区常住人口分布在500万—1000万之间的城市则新增了佛山、汕头、南京、杭州、哈尔滨;城区常住人口在300万—500万的则由原来的8个变成2010年的21个,一些中西部城市,如长沙、太原、合肥、郑州、乌鲁木齐等在这十年间人口增长速度较快,飞跃成1类大城市,这与国家支持中西部发展战略密切相关;人口处在100万—300万之间的2类大城市增长到99个城市,人口处在50万—100万之间的中等城市有96个,人口处在20萬—50万之间的小城市减少为32个。
2实证模型建立与指标选取
(1)模型建立。由于城市人口流动、城市之间的生产经营活动均具有空间联动性,因此本文通过设定空间权重wij,在(4)式基础上建立空间计量回归模型,设定如下:
g·pi,t=Bi,t+χlnN—i,0+αmlnYi,t+βnlnCi,t+ρwij×g·pi,t+εit(5)
式(5)中,g·pi,t表示城市i从t-T到t年的人口增长率,T为时间间隔,本文选取的是2000年到2010年间,各地级市的人口增长率; lnN—i,0表示城市i在基年(2000年)的人口对数值,系数χ则衡量了城市人口规模空间演化路径特性,χ显著大于0时,则表现为发散增长,χ显著小于0时,则表现为收敛增长,χ不显著时,则表现为平行增长。Yi,t为集聚收益变量矩阵,Ci,t为集聚成本变量矩阵,αm、βn为对应相关系数;εit为误差项。系数ρ表示城市之间人口增长率存在空间相关性;wij表示城市i与城市j之间相互影响的权重。本文选择包含地理特征的反距离平方权重矩阵以及包含经济特征的经济和流动网络权重矩阵。反距离平方权重衡量人口流动具有地理属性;经济距离权重说明城市经济发展水平越高,一方面越容易吸引
邻近地区的人口流入,另一方面则抑制了本地区的人口流出,从而影响整个城市的人口水平;流动网络权重说明一个地区存在人口流动,而人与人之间通过亲戚、朋友、熟人等社会纽带,会带动周边地区更多的人口流动,形成“裙带效应”。
(2)集聚收益与成本因素。根据上述相关理论分析,我们将集聚收益表现为四个方面:工资水平、就业水平、医疗水平以及教育水平;将集聚成本量化为三个方面:拥挤成本、住宅成本、污染。其中,工资水平(S),采用城市在岗职工的平均工资来表示,城市工资水平越高,相应的可支配收入也越高,可以消费更多的产品,城市居民更加能享受在此生活的便利[3,23-25]。就业水平(V),采用第三产业的就业份额来表示,一个城市第三产业的发展水平越高,一方面可以提供广阔的就业机会,吸纳人口进城,另一方面可以提供多样化服务,便利居民生活[26-27]。另外公共设施也对人口分布产生重要影响[28-29],以医疗水平(H)作为公共资源与服务的代理变量,采用市辖区医院、卫生院床位数来衡量。教育水平(E),采用普通高等学校在校大学生数来表示,一个城市的教育水平越高,越能促进城市的发展与进步,从而促进人口增长[3,25]。成本因素方面,城市的拥挤会提高通勤成本,进而影响城市人口规模[25],采用城市人均拥有道路面积的倒数作为城市通勤成本的代理变量,人均拥有城市道路面积越大,说明城市的拥挤成本(C)越小。住房成本(R),利用城市住宅商品房销售价格来衡量城市的住宅成本,城市住宅商品房销售价格越高,住宅成本也越高[23,29-30]。污染(P),选用各地级市工业二氧化硫排放量来表示。收益和成本因素的测量指标数据来自于《中国城市统计年鉴》、《中国统计年鉴》、《中国区域经济统计年鉴》以及各省及部分城市的统计年鉴。endprint
四、城市人口规模空间演化实证结果解析
1相关实证结果
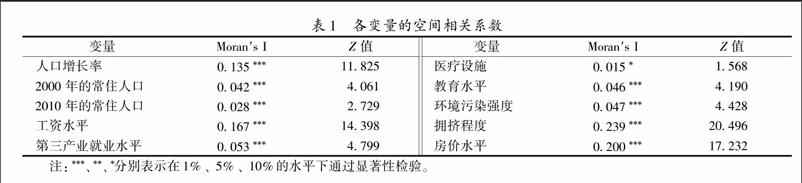
在采用空间计量模型之前,需要对相关变量的空间相关性进行检验。为此,我们采用空间Morans I指数测度方法,对回归模型中各变量的空间相关性进行测度,结果见表1。从表1中各变量空间相关系数的显著性水平来看,人口分布存在显著的空间正相关性。
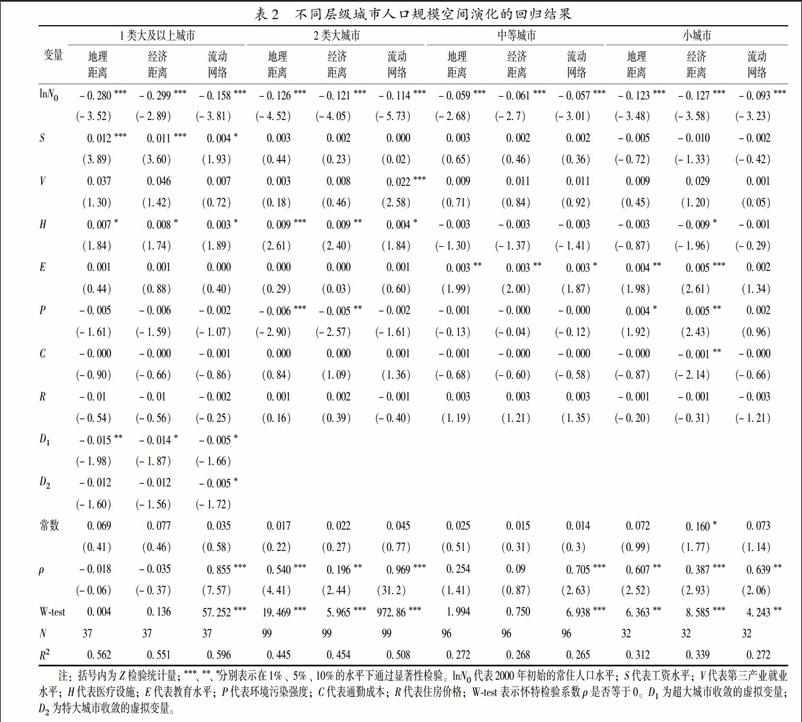
在进行实证回归时,由于超大城市样本较少,为避免多重共线性问题,将超大城市、特大城市以及1类大城市这三类城市合并,简称为1类大及以上规模城市。同时考虑到这三类城市在人口规模演化过程中都具有人口净流入这一共性,可在同一回归框架下采用虚拟变量法来比较三类城市的结果差异[31]。虚拟变量构建方法为:D1=d1×lnp0,D2=d2×lnp0,其中,d1为超大城市虚拟变量,d2为特大城市虚拟变量。表2结果显示,不同权重下回归变量的方向基本保持一致,这也在一定程度上验证了回归结果的稳健性。整体来看,不同层级城市人口规模演化路径都表现出显著的收敛增长特性,lnN—i,0的系数为负且显著;横向对比不同层级城市,1类大及以上城市的人口规模演化收敛系数最大,2类大城市和小城市系数大小相当,仅次于1类大及以上城市,中等城市的收敛系数最小。
从1类大及以上城市样本来看,3种空间权重下,人口规模演化路径表现为收敛增长特性。从虚拟变量的系数来看,D1系数绝对值高于D2,说明超大城市的收敛速度快于特大城市,而特大城市的收敛速度快于1类大城市,即城市初始等级越高,城市人口规模朝其稳态均衡规模收敛的速度越快。从影响城市人口规模演化的因素来看,工资水平、第三产业就业份额和医疗水平是影响1类大及以上城市人口规模增长的主要收益因素,而环境污染程度显著地抑制了地区的人口增长。
从2类大城市样本来看,无论在何种空间权重下,人口规模空间演化同样表现出了显著收敛增长
特性,且收敛系数大致相同。2类大城市样本的收敛系数要远小于1类大及以上城市,说明2类大城
市的人口规模发展的空间比1类大及以上城市的發展空间要大。第三产业就业份额、医疗水平是影响人口规模空间演化的主要收益因素,同样环境污染强度是影响人口规模空间演化的主要成本因素。
从中等城市样本回归结果可以看出,在三种空间权重下,人口规模演化收敛系数相差不大。中等城市样本的收敛系数要远小于大城市(包括1类大及以上城市和2类大城市,以下统称大城市),说明中等城市人口规模变动至其均衡水平要经历很长一段时间。这主要是因为样本中的大部分城市属于
人口净流出主导类型的城市(如蚌埠、焦作和周口、随州和咸宁、广安和资阳等市),这类城市人口
集聚的速度很慢,引致人口集聚带来的收益增长速度也很慢,因此其人口规模朝稳态均衡发展的速度也最慢。从影响城市人口规模演化的因素来看,教育水平是影响人口规模空间演化的主要收益因素,其成本因素并不显著,说明从中等城市现在的人口规模来看,因人口过度集聚引发的成本尚未显现。
从小城市样本来看,无论在何种空间权重下,人口规模空间演化同样表现出显著的空间收敛增长特性。小城市样本的收敛速度小于1类大及以上城市样本,接近于2类大城市样本,大于中等城市样本。教育水平是影响人口规模空间演化的主要收益因素,同时环境污染是影响人口规模空间演化的主要成本因素,这主要与这些城市的经济发展水平较低,环境污染治理不及时不规范相关。
2稳健性检验
虽然本文所采用的最大似然估计(MLE)方法一定程度上规避了模型中可能存在的内生性问题,但考虑到最大似然估计在大样本、空间权重维度较高情况下估计量可能存在的偏误,本文将利用SAR的GMM估计(又称为GS2SLS),通过选择工具变量来对模型进行GMM重新估计。GS2SLS使用的工具变量矩阵H={X,WX,…,WqX}中线性独立的列向量,通过以下步骤来进行,首先使用工具变量矩阵H对回归方程进行2SLS估计;其次将第一步中的残差代入残差方程中,计算GMM估计,得到相应的空间估计量ρ~;第三步将估计量ρ~进行空间CochraneOrcutt变换,从而去掉扰动项空间
自相关性,产生新扰动项;最后,将扰动项作为残差的估计量重新代入残差方程,进行GMM估计量[32]。为了节省篇幅,本文仅报告经济距离权重下,各样本的GS2SLS的估计量。从经济距离权重下GS2SLS估计结果中,我们可以看到,估计量与MLE方法中最大的区别在于一些变量的显著性存在差异,基本结论与MLE模型中相似,从而说明前面模型回归结果的稳健性,具体见表3。
五、主要结论与启示
本文首先从理论角度探讨了城市人口规模的空间演化机理,即城市人口规模是集聚收益与集聚成本相互权衡的结果,并在此基础上,以中国264个地级及以上城市“五普”和“六普”的常住人口数据为样本,采用城市之间地理距离、经济距离和流动网络作为空间权重矩阵,运用空间自回归模型(SAC)测度了中国不同层级样本城市人口规模空间演化特性。我们得出如下结论:①不同层级城市人口规模演化路径均表现出显著的收敛增长特性,层级最高的城市样本收敛系数最大,2类大城市和小城市收敛系数相当,仅次于1类大及以上城市,中等城市的收敛系数最慢。②从城市人口规模空间收敛的收益因素来看,第三产业就业份额、医疗水平和工资水平是1类大及以上城市样本的主要收益因素;第三产业就业份额、医疗水平是2类大城市的主要收益因素;在中等城市和小城市样本中,教育水平是主要收益因素。③从城市人口规模空间收敛的成本因素来看,环境污染强度是1类大及以上城市、2类大城市以及小城市最主要的抑制因素,而对中等城市的影响尚不明显。
本文的研究结论对于有效引导不同层级城市人口转移,发挥不同规模城市间的协同作用具有一定指导意义。在现有集聚收益与成本因素影响下,层级较高的城市,人口规模朝其稳态endprint
均衡
收敛的速度较快,超大城市(如北京、上海、广州等人口净流入城市)人口规模趋于稳态均衡收敛的速度最快,这类城市在发展过程中,调整产业、人力资本结构,自发地发挥其中心城市溢出效应,带动周边城市的发展,在缓解自身人口拥挤的压力同时,又可以提高自身的人力资本结构。而中等城市(如蚌埠、随州、咸宁等人口净流出城市)的收敛速度最慢,这类城市一方面要积极承接沿海产业转移,以承接产业转移带动人口的回流,另一方面要完善区域教育等公共服务环境以留住人才。未来的研究方向也是本文的不足之处,表现在以下两个方面:首先,没有更具体详细地厘清城市集聚收益与拥挤成本;其次,仅以城市规模作为城市分层的标准,而没有进一步考虑同一层级下人口净流入与人口净流出这两类城市的人口变动与影响因素。
参考文献:
[1]EATON J, ECKSTEIN Z. Cities and growth: theory and evidence from France and Japan[J]. Regional Science and Urban Economics, 1997,27(4):443-474.
[2]ROZENFELD H D, DIEGO R, JOSE S, et al. Laws of population growth[J].Proceedings of the National Academy of Sciences of the USA, 2008,105(48):18702-18707.
[3]GLAESER E L, PONZETTO G A M, TOBIO K. Cities, skills and regional change[J].Regional Studies, 2014,48(1):7-43.
[4]ANDERSON G, GE Y. The size distribution of Chinese cities[J].Regional Science and Urban Economics, 2005, 35(6):756-776.
[5]段學军,王书国,陈雯.长江三角洲地区人口分布演化与偏移增长[J].地理科学, 2008(2):139-144.
[6]XU Z L, ZHU N. City size distribution in China: are large cities dominant[J].Urban Studies, 2009, 46(10):2159-2185.
[7]余吉祥,周光霞,段玉彬.中国城市规模分布的演进趋势研究——基于全国人口普查数据[J].人口与经济, 2013(2):44-52.
[8]MATLABA V J, HOLMES M J. A century of the evolution of the urban system in Brazil[J].Review of Urban and Regional Development Studies, 2013, 25(3): 129-151.
[9]SCHAFFAR A, DIMOU M. Ranksize city dynamics in China and India, 1981—2004[J].Regional Studies, 2012, 46(6):707-721.
[10]DURANTON G. Urban evolutions: the fast, the slow, and the still[J].American Economic Review, 2007, 97(1):197-221.
[11]江曼琦,王振坡,王丽艳.中国城市规模分布演进的实证研究及对城市发展方针的反思[J].上海经济研究, 2006(6):29-35.
[12]CHEN Z H, FU S H, ZHANG D Y. Searching for the parallel growth of cities in China[J].Urban Studies, 2013, 50(10):2118-2135.
[13]WANG Z P, ZHU J N. Evolution of Chinas citysize distribution: empirical evidence from 1949 to 2008[J].The Chinese Economy, 2013, 46(1):38-54.
[14]王小鲁,夏小林.优化城市规模推动经济增长[J].经济研究, 1999(9):22-29.
[15]王小鲁.中国城市化路径与城市规模的经济学分析[J].经济研究, 2010(10):20-32.
[16]金相郁.最佳城市规模理论与实证分析——以中国三大直辖市为例[J].上海经济研究, 2004(7):35-43.
[17]HENDERSON J V. The sizes and types of cities[J].The American Economic Review, 1974, 64(4):640-656.
[18]DURANTON G, PUGA D. Microfoundations of urban agglomeration economies[J]. Handbook of Regional and Urban Economics, 2003, 4(4):2063-2117.
[19]ROSSI-HANSBERG E, WRIGHT M L J.Urban structure and growth[J]. Review of Economic Studies, 2007, 74(2):597-624.endprint
[20]ABDEL-RAHMAN H, FUJITA M. Product variety, Marshallian externalities, and city sizes[J].Journal of Regional Science, 1990, 30(2):165-183.
[21]陈良文,杨开忠.集聚与分散:新经济地理学模型与城市内部空间结构、外部规模经济效应的整合研究[J].经济学(季刊), 2008(1):53-70.
[22]王俊,李佐军.拥挤效应、经济增长与最优城市规模[J].中国人口·资源与环境, 2014(7): 45-51.
[23]PAULSEN K. Yet even more evidence on the spatial size of cities: urban spatial expansion in the US, 1980—2000[J].Regional Science and Urban Economics, 2012, 42(4):561-568.
[24]王桂新,潘泽瀚,陆燕秋.中国省际人口迁移区域模式变化及其影响因素——基于2000和2010年人口普查资料的分析[J].中国人口科学, 2012(5):2-13.
[25]孟兆敏,吳瑞君. 流动人口与户籍人口的收入差异及其影响因素——以上海市为例[J]. 城市问题,2016(6):82-91.
[26]AU C, HENDERSON J V. Are Chinese cities too small?[J].The Review of Economic Studies, 2006, 73(3):549-576.
[27]张耀军,岑俏.中国人口空间流动格局与省际流动影响因素研究[J].人口研究, 2014(5):54-71.
[28]SOO K T. Zipf, Gibrat and geography: evidence from China, India and Brazil[J].Papers in Regional Science, 2012, 93(1):159-181.
[29]CAMAGNI R, CAPELLOO R, CARAGLIU A. One or infinite optimal city sizes? in search of an equilibrium size for cities[J].The Annals of Regional Science, 2013, 51(2):309-341.
[30]ROZENFELD H D, RYBSKID D, GABAIX X, et al. The area and population of cities: new insights from a different perspective on cities[J].American Economic Review, 2011, 101(5):2205-2225.
[31]DALL'ERBA S, LE GALLO J. Regional convergence and the impact of European structural funds over 1989-1999: a spatial econometric analysis[J]. Papers In Regional Science, 2008,87(2):219-244.
[32]陈强.高级计量经济学及Stata应用[M].北京:高等教育出版社, 2014:586-598.
[责任编辑方志]endprint
