Forced and Natural Vibrations of an Orthotropic Pre-Stressed Rectangular Plate with Neighboring Two Cylindrical Cavities

U. Babuscu Yesil

Forced and Natural Vibrations of an Orthotropic Pre-Stressed Rectangular Plate with Neighboring Two Cylindrical Cavities

U. Babuscu Yesil1

Forced and natural vibrations of a rectangular pre-stressed orthotropic composite plate containing two neighboring cylindrical cavities whose cross sections are rectangular with rounded-off corners are investigated numerically. It is assumed that all the end surfaces of the rectangular pre-stressed composite plate are simply supported and subjected to a uniformly distributed normal time-harmonic force on the upper face plane.The considered problem is formulated within the Three-Dimensional Linearized Theory of Elastic Waves in Initially Stressed Bodies (TDLTEWISB). The influence of mechanical and geometrical parameters as well as the initial stresses and the effect of cylindrical cavities on the dynamical characteristics of the rectangular orthotropic composite plate are analyzed and discussed.

Initial stresses, vibration, cylindrical cavities, 3D FEM, orthotropic material.

1 Introduction

Many defects such as holes and cavities within structural elements subjected to external effects are responsible for the stress concentrations around them. Knowledge of the magnitude of these stress concentrations is necessary to safely use these structural elements containing holes or cavities in engineering structures. This is because the values of the stress concentrations in the case where they are close to their critical value can cause a variety of dangerous situations in structures containing such defects to arise. A wide range of research in this area has been made and continues to be studied intensively in many branches of science. These problems were extensively studied, firstly by Savin[Savin G.N.(1961)]. Since then, many aspects of these problems have been developed by many researchers such as the considered structural elements and their materials, solution methods and the theories used in the mathematical modeling of these problems. Stress concentration around two cylindrical horizontal holes in a rectangular plate was investigated in [Akbarov S.D., Yahnioglu N., Babuscu Yesil U.(2012)], Weakening Effects of Internal Part-Through Elliptic Holes in Homogeneous and Laminated Composite Plates was investigated in [Chaudhuri R.A.(2007)]. A method of finding the general solution of a system of equilibrium equations for nonthin transversely isotropic plates with a uniform pre-stress field was investigated in [Khoma I.Y., KondratenkoO.A.(2008)]. A non-contact measurement method was investigated to investigate the tensile strain field of a composites plate in the presence of stress concentrations caused by a geometrical defect consisting of circular hole in [Toubal L., Karama M., Lorrai B.(2005)]. A single-layer higher-order model for predicting the stresses at curved free boundaries of laminated composite plates subjected to inplane loading was investigated in [Zhen W., Wanji C.(2009)]. In [Zheng Y., Chang-Boo K., Chongdu C., Hyeon G.B.(2008)] the coupled influence of the Poisson’s ratio and plate thickness upon the stress concentration factor, the strain concentration factor and their relations of finite thickness plate containing a hole subjected to uniaxial tension were vastly investigated using the finite element method.

In these works consideration was given to determination of the values of the stress and strain concentrations around the holes and the effects of the geometrical and material parameters on them. However, in some research, holes which were seen as being responsible for the stress concentration under loading were used for reduction of the stress concentration around the discontinuities i.e. around the other holes. An overview of various techniques developed for analysis as well as the mitigation of stress concentration in plates with singularities is given by S. Nagpal et al. [Nagpal S., Jain N., Sanyal S.(2012)]. But all the above-mentioned research is related to the corresponding problem in the static case. However, it has been established that stress concentrations significantly affect the dynamical characteristics of plates containing holes. The forced vibration of an initially statically stressed rectangular plate made of an orthotropic material with a cylindrical hole was investigated in [Akbarov S.D., Yahnioglu N., Babuscu Yesil U.(2010)]. An analysis of the forced vibration of an initially stressed rectangular transversally isotropic plate containing two neighboring cylindrical cavities was investigated in [Akbarov S.D., Yahnioglu N., Babuscu Yesil U.(2012)]. Coupling method was investigated for free vibration analyses of rectangular plate with a rectangular or circular hole in [Kwaka M.K., Han S.(2007)]. Free vibration analysis of composite plates in the presence of cutouts undergoing large amplitude oscillations was investigated in[Sivakumar K., Iyengar N.G.R.(1999)]. Stress distribution in the pre-stretched simply supported strip containing two neighbouring circular holes under forced vibration was investigated in [Yahnioglu N.(2007)]. The influence of the initial stretching of a composite thick plate containing a cylindrical hole on the stress concentration around a hole caused by the action of the additional uniformly distributed dynamic (time-harmonic)normal forces on the upper face of the plane was investigated in [Yahnioglu N., Babuscu Yesil U.(2009)]. The first aim is to determine the magnitude of the stress concentrations around the defects; the second aim is to find ways of reduction for these concentrations.One way to reduce the values of the stress concentrations around the defects is the use of pre-stressed materials in elements of structures with defects. The effects of initial stresses on the stress concentration around holes were investigated in some papers as mentioned above.

The present study extends the study [Akbarov S.D., Yahnioglu N., Babuscu Yesil U.(2010)] for the case where the pre-stressed orthotropic rectangular plate contains two equal internal parallel neighboring cylindrical cavities (lying width-wise in the plate)with rectangular cross sections with rounded corners. And the present study extends the study [Akbarov S.D., Yahnioglu N., Babuscu Yesil U.(2012)] by taking the plate’s material as orthotropic and extends the study [Akbarov S.D., Yahnioglu N., Babuscu Yesil U.(2012)] by examining the dynamical characteristics of the plate. Mathematical modeling is made within the TDLTEWISB and according to this theory, initial stress distributions are determined in the considered plate by employing the linear elasticity theory and then, using the equations and relations of the TDLTEWISB containing the initial stress distributions in the plate, the forced and natural vibrations of the pre-stressed rectangular orthotropic plate are investigated. It is assumed that the initial stresses are caused by the uniformly distributed normal forces acting on two opposite end-planes which are normal to the direction in which the cylindrical cavities lie. Both determination of the initial stresses and the dynamical quantities such as the fundamental frequencies and stress concentrations under vibration of the considered rectangular plate are calculated numerically by using 3D finite element modeling. The influence of the geometrical and mechanical parameters of the orthotropic plate and interaction between the cavities, as well as the initial stresses on the dynamical characteristics of the considered plate are analyzed and discussed.

2 Formulation of the problem

Figure 1: The geometry of the considered rectangular plate including two equal cylindrical cavities

In the considered problem, the solution domain occupies the region:

Figure 2: Loading of the considered rectangular plate including two equal cylindrical cavities

According to the above discussion, to determine the initial stress-state, the following boundary-value problem can be solved.

Equilibrium equations:

Mechanical Relations:

Geometrical Relations:

Boundary Conditions:

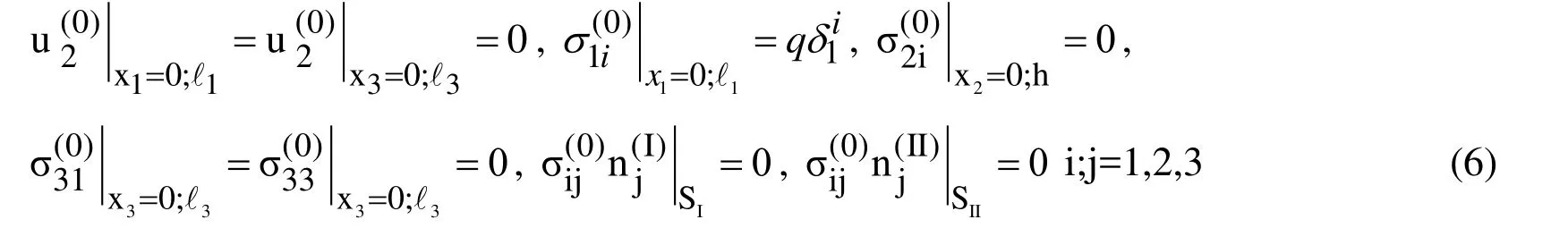
To determine the stress-state caused by additional dynamic loading, the following boundary-value problem must be solved.

TDLTEWISB equations of motion [Akbarov S.D., Yahnioglu N., Babuscu Yesil U.(2012), Guz A.N. (2004)]:

Mechanical relations

Geometrical relations:

Boundary conditions:

In (7)-(10) conventional notation is used. It is assumed that the plate material is an orthotropic one with elastic symmetry axes Ox1,Ox2and Ox3. So matrix D in (4) and(8) is given as follows:

where, according to [Christensen R.M.(1979]],

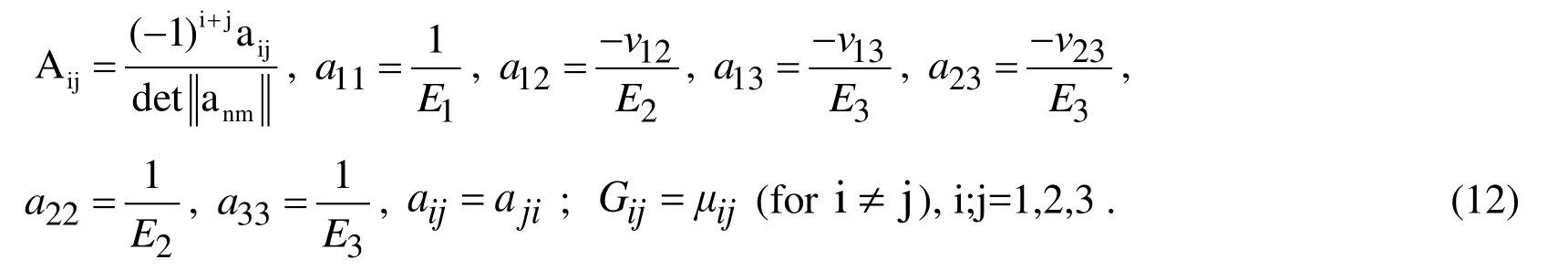
where the quantities with over-bars denote the amplitude of the corresponding quantities.For simplicity, below it is omitted these over-bars. Substituting expression (13) into Eq.(7)-(10) and doing some manipulations, the following equation in terms of the amplitude of the corresponding quantities is obtained:

Eventually, the investigation of the boundary value problem of the stress-state caused by additional dynamic loading is reduced to the solution of the boundary value problem given in Eqs. (8)-(10), (14) and (15). Note that the case wherep=0in (15) corresponds to the natural vibration problem of the plate under consideration. Thus, the mathematical formulation of the considered problem is fully defined.

3 Solution method: finite element formulation

The foregoing boundary value problems will be investigated by employing 3D FEM modeling. The displacement-based finite elements for the FEM modeling is used. It means that unknown values at each node of a finite element are selected displacements only [Zienkiewicz O.C., Taylor R.L.(1989)]. For this purpose, for the FEM modeling of the boundary value problem in (3)-(6), the functional

is introduced and for the FEM modeling of the problem (8)-(10), (14) and (15) the functional

Figure 3: a) The finite elements mesh around the cylindrical cavity;b)The geometry of the brick and the triangular prism finite elements.

For the solution to the considered boundary value problems, the functions of the displacements in each finite element are determined as polynomial functions in terms of shape functions and unknown values of the displacement at the nodes of that element.

In Eq. (21) p equals 8 (6) for a brick (a triangular prism) finite element. For the rectangular finite element, the second-order standard Lagrange-family shape functions are used at nodes in normalized coordinates [Zienkiewicz O.C., Taylor R.L. (1989)]. For calculating the shape functions of triangular prism finite elements, triangular pyramids are used. For this purpose each triangular prism element divided into three triangular pyramidal elements (Fig. 4)

Figure 4: Separation of triangular prism elements into triangular pyramidal finite elements

Figure 5: Triangular pyramidal finite elements

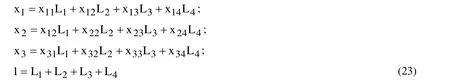
Substituting Eq. (20) into Eq. (16) and Eq. (17), after some mathematical manipulations,finally yields the following system of algebraic equations are obtained as follows:

The system for the algebraic equation for the first boundary value problem ((3)-(6))

and the system for the algebraic equation for the second boundary value problem ((8)-(10), (14) and (15))

The solutions to Eqs. (24) and (25) give the values of the displacements at each node.However, equation (25) includes the values of the stresses obtained from the solution to the first boundary value problem. So, before finding the solution to Eq. (25), the distribution of the stresses for the first boundary value problem should be found. Using the solution to Eq. (24) and Hooke’s Law, they are obtained. Furthermore, the fundamental frequency of the considered plate can be determined from equation:

Note that the same number of finite elements is taken and the same arrangements are used for the FEM modeling in obtaining the numerical solutions of the considered problems. The normalized coordinates for the brick finite elements and Gauss quadrature method are used for the calculation of the numerical integrals with ten sample points in each finite element. Volume coordinate for the triangular prism finite elements is used and numerical integrals are calculated with formula (30) for triangular pyramidal finite elements [Zienkiewicz O.C., Taylor R.L. (1989)].

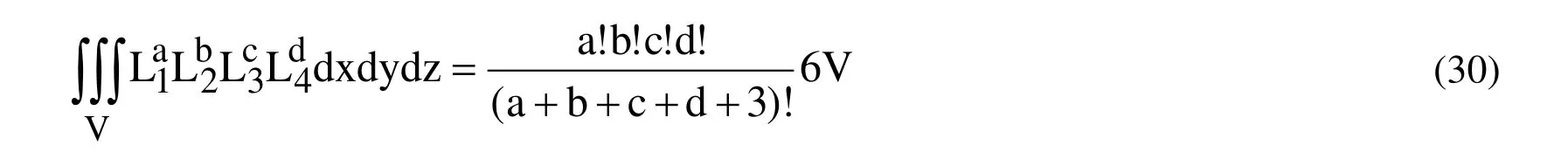
Thus, the discussion above completes consideration of the FEM modeling of the formulated problem.

4 Numerical results and discussions

2 1 E E 3 1ℓℓ1 2 3 4 A k b a r o v a n d G u z(2 0 0 0)1 0.2 3 0.0 9 0.0 8 0.0 7 0.0 6 1 0 0.5 6 0.2 4 0.2 1 0.1 9 -2 0 0.9 3 0.4 1 0.3 5 0.3 3 0.3 1 5 0 1.9 2 0.8 0 0.7 0 0.6 7 0.6 2

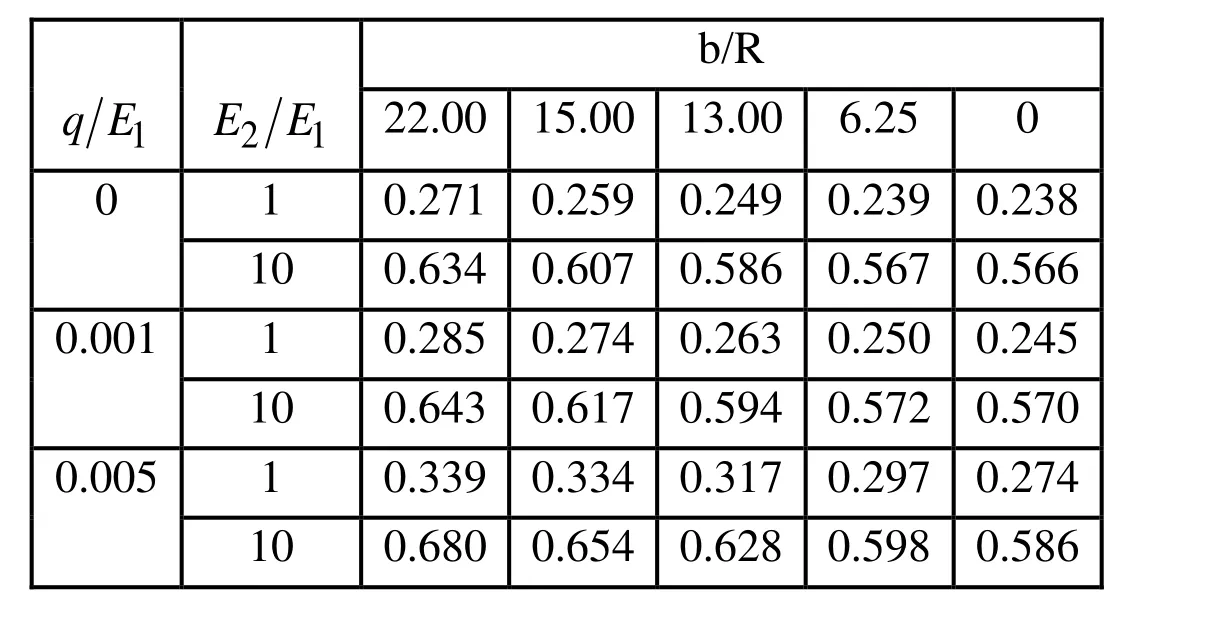
b/R 1 q E 2 1EE 22.00 15.00 13.00 6.25 0 0 1 0.271 0.259 0.249 0.239 0.238 10 0.634 0.607 0.586 0.567 0.566 0.001 1 0.285 0.274 0.263 0.250 0.245 10 0.643 0.617 0.594 0.572 0.570 0.005 1 0.339 0.334 0.317 0.297 0.274 10 0.680 0.654 0.628 0.598 0.586

?

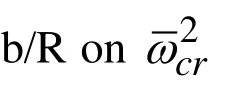
c/R 1 q E A centered Single Cavity 3.25 5.50 7.75 14.50 21.25 0 0.186 0.246 0.252 0.279 0.307 0.347 0.005 0.258 0.353 0.358 0.372 0.402 0.441 0.010 0.327 0.435 0.439 0.459 0.492 0.531

1 q E3 1/EE 0.3 0.5 2 1/EE 0.3 0.5 0.3 0.5 0 0.178 0.0154 0.379 0.279 0.005 0.234 0.203 0.501 0.372 0.010 0.285 0.249 0.613 0.459

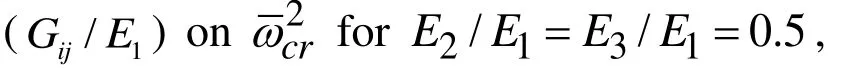
13 1/ 0.1 G E=12 1/ 0.1 G E=13 1/ 0.1 G E=1 q E 23 1/ 0.1 G E=12 1/G E 23 1/ 0.1 G E=13 1/G E 12 1/ 0.1 G E=23 1/G E 0.1 0.05 0.01 0.1 0.05 0.01 0.1 0.05 0.01 0 0.279 0.225 0.120 0.279 0.248 0.206 0.279 0.268 0.250 0.005 0.372 0.333 0.213 0.372 0.343 0.287 0.372 0.376 0.402 0.010 0.459 0.419 0.295 0.459 0.414 0.345 0.459 0.479 0.533

1 q E 2 cr ω 0.010 0.005 0.001 0.000 -0.001 -0.005 -0.010 0.459 0.372 0.298 0.279 0.260 0.181 0.077

1 q E Uh R 5 4 3 2 0 0.279 0.278 0.274 0.266 0.005 0.372 0.345 0.311 0.260 0.010 0.459 0.406 0.342 0.248

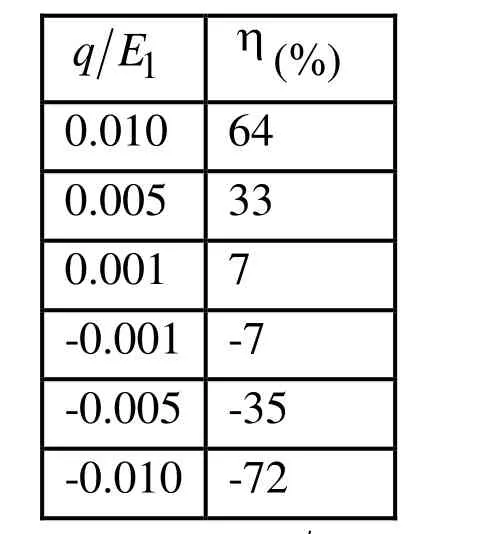
1 q E η(%)0.010 64 0.005 33 0.001 7-0.001 -7-0.005 -35-0.010 -72

Figure 6: The distribution ofwith respect toθunder various initial forcesin the case where

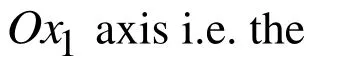
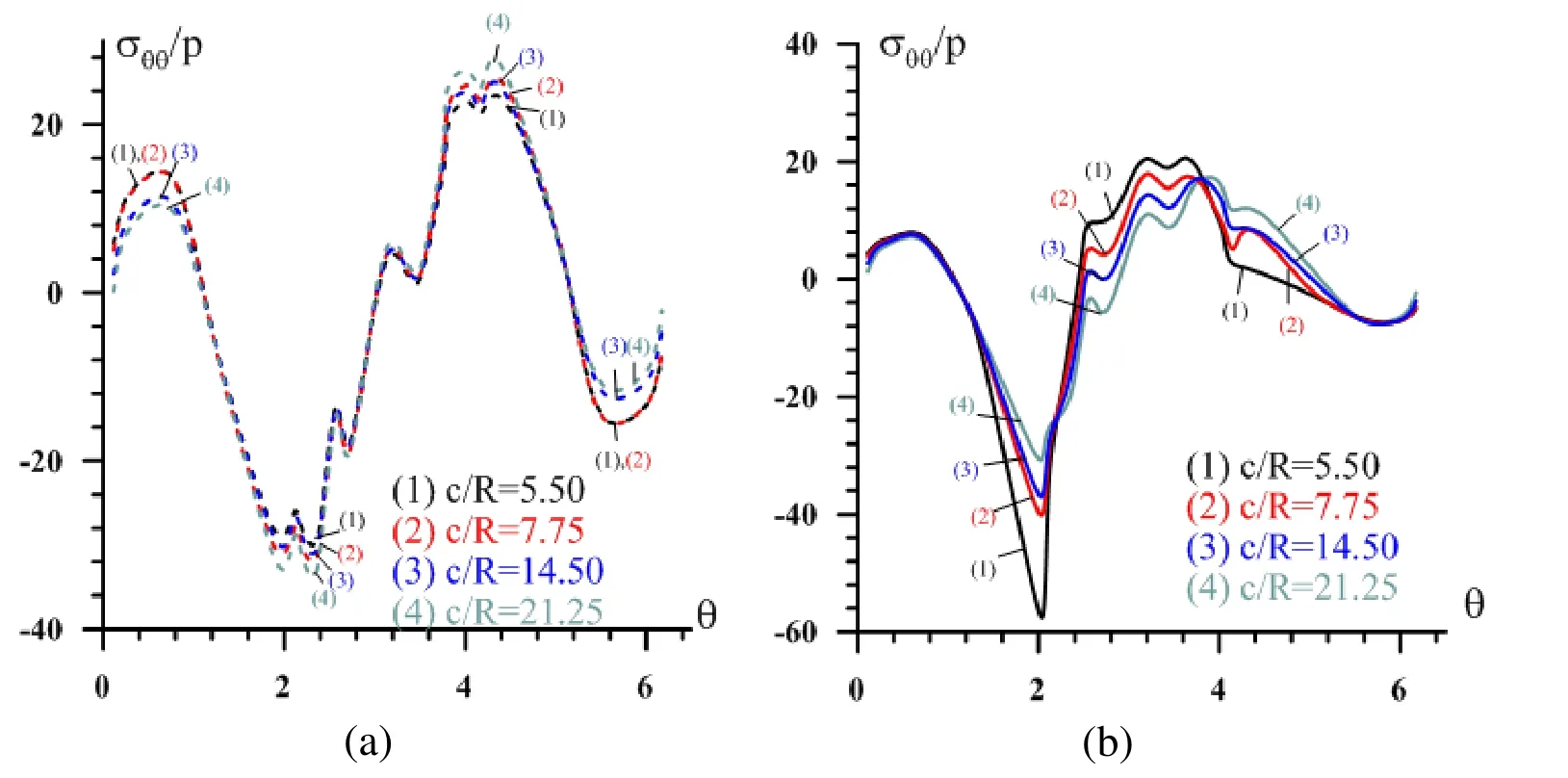
Figure 7: The distribution ofwith respect to θunder various distances between the cavities in the case where

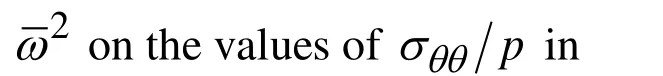
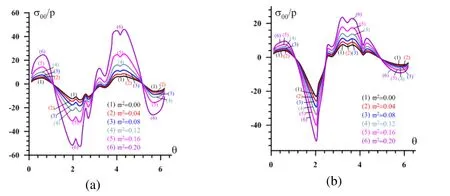
Figure 8: The influence ofwith respect to θa) forin the case where

Figure 9: The influence ofon the values (b) in the case where

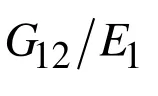
Figure 10: The influence ofon the values of

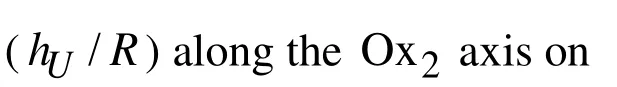
Figure 11: The distribution ofwith respect toθunder various thicknesses between the upper plane of the cavities and upper face-plane of the plate, i.e.the case where

Figure 12: The distribution ofwith respect to θunder various(b) in the case where

5 Conclusions

Thus, in the present paper, within the scope of the Three-Dimensional Linearized Theory of Elastic Waves in Initially Stressed Bodies (TDLTEWISB), natural and forced vibration of a rectangular pre-stressed plate containing two neighboring equal parallel cylindrical cavities (lying width-wise in the plate) whose cross sections are rectangular with rounded-off corners has been investigated. It was assumed that the material of the plate is orthotropic. The investigations were carried out by employing 3D FEM modeling.

First, the initial stress state caused by uniform stretching forces acting on two end planes of the plate was determined using the linear theory of elasticity. Next, the stress state caused by time–harmonic forces acting on the upper free face plane of the plate was determined. All the end surfaces of the plate are simply supported. Numerical results on the dynamical stress concentrations around the holes and the influence of the orthotropic material properties and the influence of initial stretching on these concentrations, as well as interaction between the holes were presented and compared with the corresponding numerical results for transversely isotropic plate with two cylindrical cavities and for a plate without holes.

From the numerical results obtained, the following inferences can be drawn:

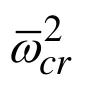
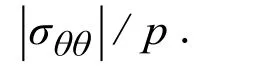
AcknowledgementThe author is grateful to Prof. Dr. Surkay D. AKBAROV for comments and discussions and Prof. Dr. Nazmiye YAHNIOGLU for considerable revision of the manuscript.

Akbarov S.D., Guz A.N.,2000,Mechanics of Curved Composites, Kluwer Academics Publisher, Dordrecht.

Akbarov S.D., Yahnioglu N., Babuscu Yesil U.,2010, Forced Vibration Of An Initially Stressed Thick Rectangular Plate Made of an Orthotropic Material With A Cylindrical Hole,Mech. of Comp. Mat., 46, 3, 287-298.

Akbarov S.D., Yahnioglu N., Babuscu Yesil U.,2012, 3D Analysis of the forced vibrations of a prestressed rectangular composite plate with two neighboring cylindrical cavities,CMC (Computers, Materials & Continua), 28, 2, 147-164.

Akbarov S.D., Yahnioglu N., Babuscu Yesil U.,2012, 3D FEM Analysis of Stress Concentrations Around Two Neighboring Cylindrical Holes Wıthin a Pre-Stressed Rectangular Composite Plate Under Bending,Mech. of Comp. Mat., 48, 5, 499-510.

Chaudhuri R.A.,2007, Weakening Effects of Internal Part-Through Elliptic Holes in Homogeneous and Laminated Composite Plates,Composites Structures, 81, 362-373.

Christensen R.M.,1979,Mechanics of Composite Materials, John Willey and Sons, Int.New York.

Guz A.N.,2004,Elastic waves in bodies with initial (residual) stresses. ”A.C.K.”, Kiev.Khoma I.Y., Kondratenko O.A.,2008, Stress distribution around a circular cylindrical cavity in a prestressed plate,International Applied Mechanics, 44, 1, 23-33.

Kwaka M.K., Han S.,2007, Free vibration analysis of rectangular plate with a hole by means of independent coordinate, coupling method,J. Sound Vibr., 306, 12-30.

Nagpal S., Jain N., Sanyal S.,2012, Stress concentration and its mitigation techniques in flat plate with singularities-a critical review,Eng. Jour.16, 1, 1-15.

Savin G.N.,1961,Stress Concentration Around Holes, E. Gros Translator, Pergomon.

Sivakumar K., Iyengar N.G.R.,1999, Free vibration of laminated composite plates with cutout,J. Sound Vibr., 221, 3, 443-470.

Toubal L., Karama M., Lorrai B.,2005, Stress concentration in a circular hole in composite plate,Composite Structures, 68, 1, 31-36.

Yahnioglu N., 2007, On the stress distribution in the pre-stretched simply supported strip containing two neighbouring circular holes under forced vibration,Int. Appl. Mech., 43,10, 135-140.

Yahnioglu N., Babuscu Yesil U.,2009, Forced vibration of an initial stressed rectangular composite thick plate with a cylindrical hole,ASME 2009 International Mechanical Engineering Congress and Exposition IMECE09, November 13-19, Lake Buena Vista, Florida, USA.

Zhen W., Wanji C.,2009, Stress analysis of laminated composite plates with a circular hole according to a single-layer higher-order model,Composite Structures, 90, 122-129.

Zheng Y., Chang-Boo K., Chongdu C., Hyeon G.B.,2008, The concentration of stress and strain in finite thickness elastic plate containing a circular hole,InternationalJournal of Solids and Structures, 45, 3-4, 713-731.

Zienkiewicz O.C., Taylor R.L.,1989,The Finite Element Methods: Basic Formulation and Linear Problems, vol. 1,4thEd., Mc Graw-Hill Book Company, Oxford.

1Department of Mathematical Engineering, Faculty of Chemical and Metallurgical Eng., Yildiz Technical University, Davutpasa Campus, 34210, Esenler, Istanbul, Turkey.

E-mail:ubabuscu@yildiz.edu.tr