基于位置社会网络的双重细粒度兴趣点推荐

廖国琼 姜 珊 周志恒 万常选

1(江西财经大学信息管理学院 南昌 330013) 2(江西省高校数据与知识工程重点实验室(江西财经大学) 南昌 330013)

基于位置社会网络的双重细粒度兴趣点推荐

廖国琼1,2姜 珊1周志恒1万常选1,2

1(江西财经大学信息管理学院 南昌 330013)2(江西省高校数据与知识工程重点实验室(江西财经大学) 南昌 330013)

兴趣点推荐是在基于位置社会网络(location-based social network, LBSN)中流行起来的一种全新形式的推荐.利用LBSN所包含的丰富信息进行个性化推荐能有效增强用户体验和提高用户对LBSN的依赖度.针对无显示用户偏好、兴趣非一致性和数据稀疏性等挑战性问题，研究一种针对LBSN的双重细粒度POI推荐策略，即一方面将用户的全部历史签到信息以小时为单位细分为24个时间段，另一方面将每个POI细分为多个潜在主题及其分布，同时利用用户的历史签到信息和评论信息挖掘出用户在不同时间段的主题偏好，以实现POI的Top-N推荐.为实现该推荐思路，首先，根据用户的评论信息，运用LDA模型提取出每个POI的主题分布;然后，对于每个用户，将其签到信息划分到24个时间段中，通过连接相应的POI主题分布映射出用户在不同时间段对每个主题的兴趣偏好.为解决数据稀疏问题，运用高阶奇异值分解算法对用户-主题-时间三阶张量进行分解，获取用户在每个时间段对每个主题更为准确的兴趣评分.在真实数据集上进行了性能测试，结果表明所提出的推荐策略具有较好的推荐效果.

兴趣点推荐；基于位置社会网络；LDA主题模型；兴趣映射；张量分解

随着移动设备和全球定位系统(GPS)的快速发展，近年来出现了一种以Foursquare和Gowalla为代表的基于位置社会网络(location-based social network, LBSN)，将用户的线上活动和线下交互有机地结合在一起.LBSN除允许用户添加好友形成传统意义上的在线社会网络外，还能提供主动签到(check-in)功能，帮助用户与好友即时分享正在访问的兴趣点(point-of-interest, POI)信息.

兴趣点是指用户能够获取某种服务或享受乐趣的特定地点，如咖啡厅、餐馆、电影院等.图1是一个典型的LBSN结构，包含3个层次信息，即地理位置层(签到位置)、社会关系层(朋友关系)和内容层(对兴趣点的评论、照片及视频等).有效利用LBSN中所包含的丰富信息进行兴趣点推荐能增强用户体验和提高用户对LBSN的依赖度.

然而，与传统书籍、电影及商品推荐相比，POI推荐主要面临3个挑战：

1) 无显示用户偏好.虽然LBSN中存在大量签到信息，但它们只能反映用户访问过某个POI这个事实，而不能简单认为用户在某位置签到就是喜欢，未签到就是不喜欢[1].因此，挖掘用户隐式偏好是POI推荐应考虑的首要问题.

2) 兴趣非一致性.通常来讲，不同用户在不同时间的兴趣偏好是不一致的.例如有的人喜欢早晨去喝咖啡，下午健身，晚上去KTV；而有的人喜欢早晨健身，下午去KTV，晚上去喝咖啡.因此，POI推荐策略应为时间感知策略，即能根据不同时间进行兴趣点的个性化推荐[2].

3) 数据稀疏性.众所周知，LBSN中存在大量兴趣点，而每个用户的签到信息十分有限，故签到数据较为稀疏[3].

因此，传统推荐策略已不能很好地应用于LBSN中的POI推荐.近几年来，POI推荐得到了学者们的关注，以下分别从用户偏好挖掘、时间感知推荐和数据稀疏性3个方面对相关研究进行分析.

1) 用户偏好挖掘.用户兴趣偏好主要是从用户的签到信息或评论信息中来获取.文献[4]将用户的签到次数和用户对POI的情感指向融合到一个矩阵分解模型中进行推荐.该策略考虑了两者对用户行为的影响.文献[5]采用LDA方法提取兴趣点的主题分布以及用户兴趣的主题分布，然后将两者进行匹配获取用户的兴趣偏好.但是，这2种方法都未考虑用户兴趣的非一致性特征，即认为用户的兴趣在任何时间都一样.文献[6]基于协同过滤方法计算用户的偏好，但该方法过于依赖历史数据.文献[7]利用HPY(hierarchical Pitman-Yor)语言模型处理用户的历史签到信息，并以此为依据计算用户的偏好;但该模型仅考虑了用户的签到次数，其准确率有待提高.

2) 时间感知推荐策略.时间因素在POI推荐中得到越来越多的关注.文献[8]首次提出时间感知推荐策略，通过增添时间维度拓展基于用户的协同过滤方法，其优点在于能计算出不同时间段的用户兴趣.文献[9]强调了时间非均匀性和连续性特征，将用户签到信息按小时划分到24个矩阵中，并利用矩阵分解方法和余弦相似度计算连续时间段内用户偏好的相似性.但是，将签到信息划分到24个小时的矩阵中后，使得原本就稀疏的签到信息变得更加稀疏.文献[10]提出一种基于图的推荐方法，同样将时间以小时为单位进行划分，然后将时间段、兴趣点和用户作为图中的3类节点进行连结，有效地表示了用户历史签到数据中时间与地点的关系;但该模型过于复杂，一旦改变时间段划分标准，就会导致图结构发生巨大变化.

3) 数据稀疏特征.在LBSN中，用户签到信息的稀疏特征比传统商品推荐更为明显.文献[11]采用传统基于记忆的协同过滤方法进行推荐，但容易遭遇数据稀疏问题.这是因为无论是用户还是兴趣点之间的相似度，都是基于完整的共同签到数据，而现实情况是不同用户或兴趣点所共享的签到数据较少.文献[12]利用非负贝叶斯矩阵分解方法将地理位置因素和文本内容结合在一起，能处理非零值和零值签到数据，但其不能较好地处理稀疏数据中的缺失值.文献[13]提出一种利用多元中心高斯模型处理地理位置影响，并将其与矩阵分解模型相结合进行推荐，但该方法只能处理非零值签到数据，且不适用于多维数据场合.文献[14]提出基于用户的历史签到数据构建用户-位置-时间三阶张量，并采用张量分解法进行兴趣点推荐.该方法能较好地解决数据稀疏问题，但其仅根据签到次数来确定用户的兴趣偏好，而未考虑POI的主题特征.

除以上研究外，学者们还提出了考虑地理位置因素、社会朋友关系因素、用户情感因素、POI流行程度等不同特征的POI推荐策略[15-23]，都能不同程度提高POI推荐效果.

综上所述，已有兴趣点推荐方法都只在某些方面解决了兴趣点推荐所面临过的上述挑战问题.本文拟研究一种双重细粒度POI推荐策略，即一方面将每天的时间细分为24个时间段，利用用户的历史签到信息和评论信息挖掘出用户在每个时间段的隐式主题偏好，即时间感知主题偏好；另一方面，将每个POI细分为潜在主题及相应的权重，通过计算给定时间的用户的主题偏好和POI的主题分布之间的相似度进行推荐.在该推荐策略下，不仅使用了用户的历史签到信息，而且结合了用户签到POI的评价信息，在两者的共同作用下获取用户在不同时间段的隐式兴趣偏好.同时，通过使用张量分解方法填补偏好的空缺值，可有效解决数据稀疏性问题，从而提高POI推荐的准确性.

1 问题定义及推荐框架

本文拟研究问题为，在给定时间点向用户推荐其最感兴趣的兴趣点，具体如下：

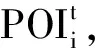
本研究整体推荐框架如图2所示:

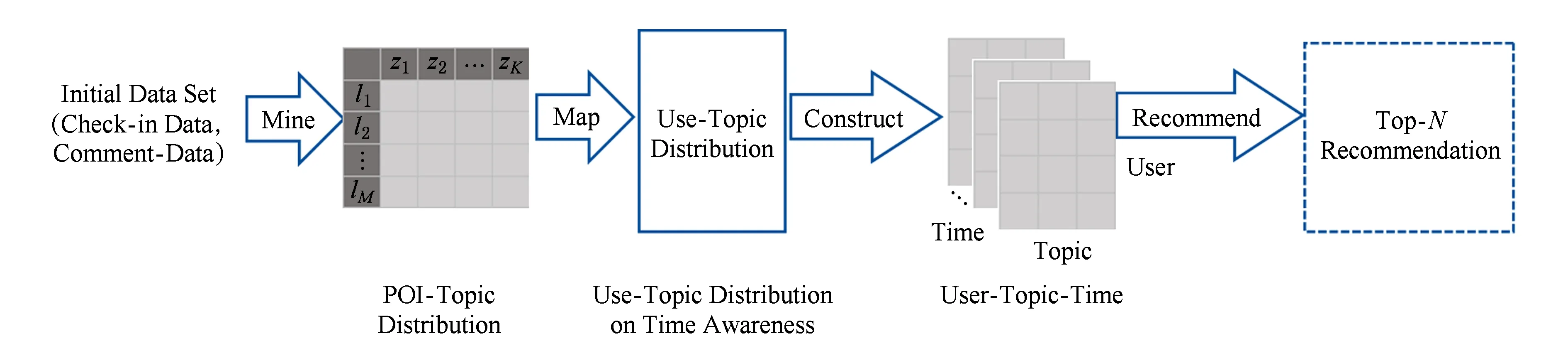
Fig. 2 Overall recommendation framework图2 整体推荐框架

图2包括以下步骤：

1) 提取POI主题分布.基于用户评论信息，利用LDA模型提取出全部POI的潜在主题分布.

2) 挖掘用户的时间感知主题偏好分布.将用户历史签到信息分为24个时间段，根据POI的主题分布，映射出用户在每个时间段的潜在主题偏好分布.

3) 张量分解.建立用户-主题-时间三维张量，通过张量分解方法，获取用户在24个时间段中更为准确的主题偏好分布.

4) 利用计算得到的时间感知主题偏好.生成给定用户特定时间点的Top-N个POI推荐列表，从而实现个性化推荐.

2 POI-主题提取及兴趣映射

首先，利用LDA(latent Dirichlet allocation)主题模型提取每个POI包含的主题分布；然后，利用离散变量的概率质量函数将签到信息与POI主题分布相结合，映射得到用户的时间感知主题偏好分布.

2.1主题提取

LDA模型是一种语言模型，通过对自然语言进行建模识别出大规模文档集合或语料库中隐藏的主题信息.在该模型中，每个文档表示为多个主题的概率分布，每个主题表示为一组单词的概率分布.因此，该模型包含2个隐性变量：主题-单词分布Φ和文档-主题分布Θ.

主题提取的目标是根据全部用户对POI的历史评论信息提取出每个POI的主题分布.我们将全部POI的所有评价信息聚合到一个POI文档中，并通过图3所示的LDA模型[5]，生成每个文档的主题分布.

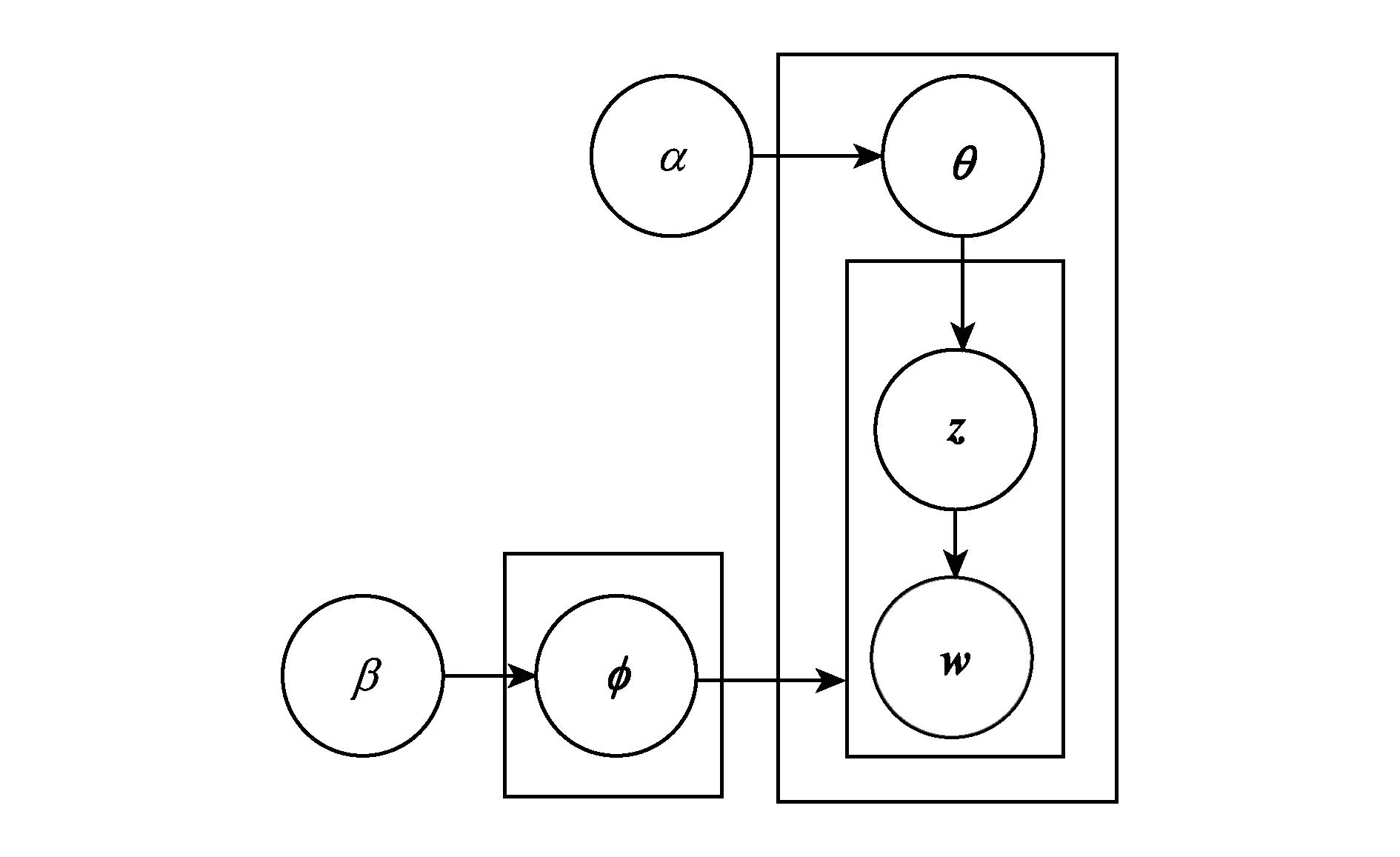
Fig. 3 LDA topic generation model图3 LDA主题生成模型

图3中各参数的意义为

1) α和β为语料级别先验参数，α代表每个文档下主题多项分布的Dirichlet先验参数，β代表每个主题下单词多项分布的Dirichlet先验参数；

2)θ和φ是隐含变量，θ表示每个兴趣点与主题之间的多项分布，φ表示每个主题与语料库单词之间的多项分布；

3)w是显示可观察到的单词向量，z是隐含的主题向量.wm,n表示第m个文档中的第n个单词；zm,n表示第m个文档中第n个单词所对应的主题.

基于LDA模型的POI主题分布生成过程如算法1所示：

算法1. POI主题生成算法.

输入： K、α、POI描述文档、单词语料库；

输出：z，Φ，Θ.

for all topick∈[1,K] do

sample mixture componentsφk～Dir(β)；

end for

/*文档层面*/

for all documentsm∈[1,M] do

sample mixture proportionφm～Dir(α)；

/*单词层面*/

for all wordsn∈[1,Nm] in documentmdo

sample topic indexzm,n～Mult(θm)；

sample word indexwm,n～Mult(φzm,n)；

end for

end for

利用LDA模型可生成2个矩阵：

1) 主题-单词概率矩阵ΦK×V，K是主题个数，V是数据集中不重复的单词个数，向量φi为第i个主题的概率分布；

2) 兴趣点-主题概率矩阵ΘM×K，其中M是POI个数，K是主题个数，向量θi为第i个POI的主题概率分布.

未知隐含变量θ和φ可通过式(1)求解得到.

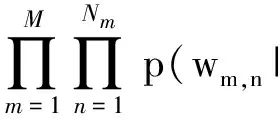
本文利用吉布斯采样(Gibbssampling)算法进行参数{Θ,Φ}学习估计.该算法是每次选取概率向量的一个维度，通过固定其他维度的值抽样当前维度值，重复迭代直到收敛，从而得到最终的主题-单词分布Φ和文档-主题分布Θ.

本研究的主要目的是要获取每个主题的权重信息.以兴趣点2612和2681为例，通过LDA模型得到的POI-主题分布如表1所示:

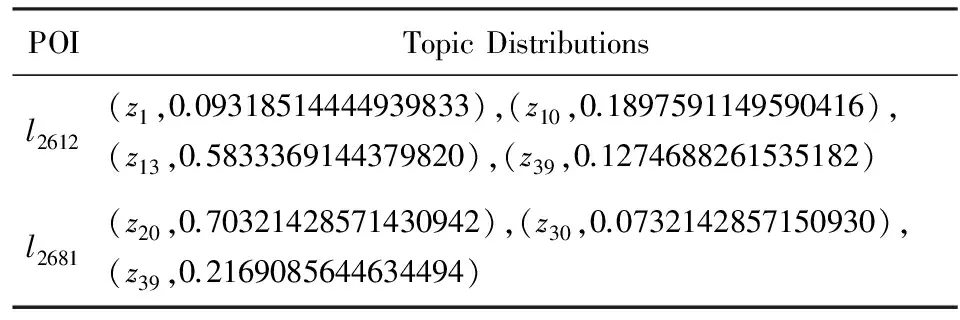
Table 1 The Examples of Results on POI-Topic Distribution表1 POI-主题分布结果示例

可以看出，2612号兴趣点隶属4个主题：1，10，13，39；2681号兴趣点隶属3个主题：20，30，39.每个主题都有相应的权重.例如，2612号兴趣点第1个主题的权重约为0.093 2.一个POI隶属的全部主题权重之和为1.

该算法单次迭代的时间复杂度为O(K×C)，其中K是主题个数，C是单词总数.多次迭代的时间复杂度为O(K×C×r)，其中r为迭代次数.

2.2兴趣映射

基于得到的POI-主题分布信息，进一步将用户的历史签到信息按24个小时进行分片，映射出用户的时间感知主题兴趣分布，如图4所示：

具体步骤如下：

1) 根据原始POI评价信息，利用算法1提取出各个POI的主题分布表，如图4的POI-Topic Distri-bution图所示；

2) 将每个用户的签到数据根据签到时间划分成24个时间切片，并统计每个时间片的签到次数，得到每个用户的时间感知签到数据表，如图4的Time-Aware Check-in Data图所示；

3) 通过连接POI-主题分布表和时间感知签到数据表，映射出用户的时间感知兴趣，得到时间感知的用户-主题分布，如图4的Time-Aware User-Topic Distribution图所示.

具体兴趣映射过程如下：

1) 统计每个用户在每个时间段对每个主题所对应的所有兴趣点签到次数，以及对于该主题的签到总次数.

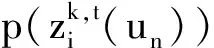
以用户2为例，其数据连接示例如表2所示.在第18个时间段，用户2对于隶属于第39个主题的2个兴趣点2612和2681的签到次数分别为1和2，故签到总次数为3,可以得出2个兴趣点的签到次数比率分别为33.3%和66.7%.

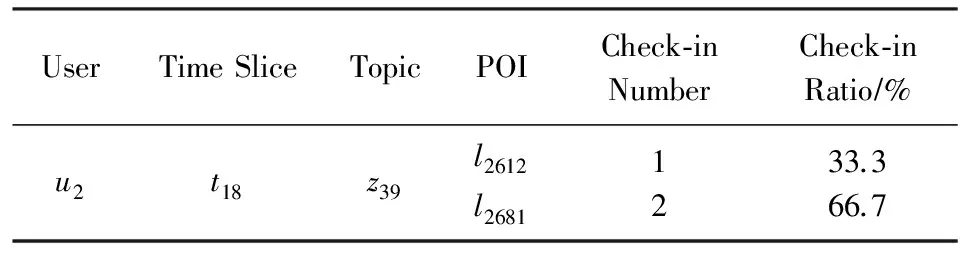
Table 2 Examples of Data Connecting表2 数据连接示例

3) 利用概率质量函数(probability mass function， PMF)计算时间感知主题兴趣偏好初始得分，即将该主题下每个POI的签到次数比率与该主题所对应POI中的权重相乘后求和.

设Zk,t(un)表示用户un在第t个时间段对于第k个主题的兴趣偏好初始得分，其计算为

根据式(3)，可以计算用户2在第18个时间段，对于第39号主题的初始兴趣偏好：

Z39,18(u2)= 0.127 468 83×33.3%+
0.216 908 56╳66.6%=0.187 095 34.

由式(3)得到的每个主题的兴趣初始偏好得分只反映用户在每个时间段对每个主题的访问偏好，而未考虑在该时间段对其他主题的访问情况.为能对用户在同一时间段全部主题的兴趣偏好进行比较，需将用户在同一时间段下的不同主题的兴趣偏好初始值进行标准化处理.

设δk,t(un)为标准化因子，表示用户un在第t个时间段对第k个主题的签到总次数Ck,t(un)与在该时间段上所有主题的签到总次数之和的比值，K为在第t个时间段访问全部主题数，则δk,t(un)计算为

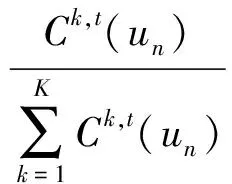
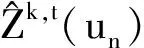
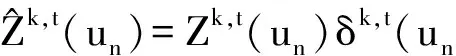
同样以用户2为例，其最终的兴趣偏好的标准化处理如表3所示.用户2在第18个时间段共签到过3个主题：39，51，60，每个主题的初始兴趣偏好由步骤1～3计算得到.在该时间段上全部签到总次数之和为6，故3个主题的标准化因子分别为12(36)，16，13(26)，乘以各自的兴趣偏好初始得分后，即可得到该用户在该时间段下对于不同主题的最终偏好得分.

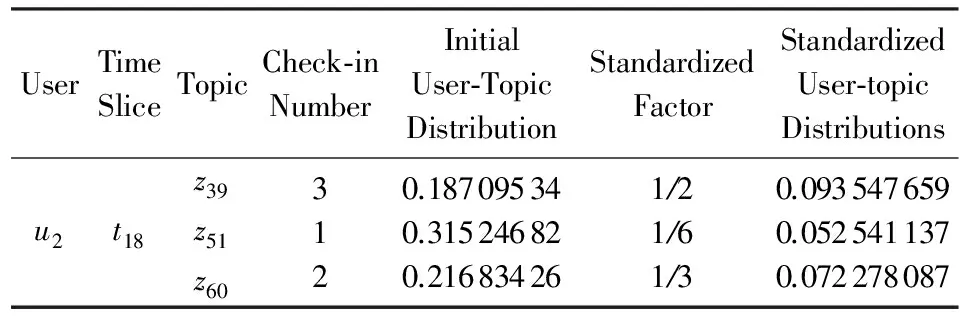
Table 3 Examples of Dealing Standardly表3 标准化处理示例

3 用户-主题-时间张量分解

张量分解(tensor factorization, TF)是对矩阵分解的拓展，其原理是通过对高维张量进行分解，生成稠密的预测张量逼近原始张量.由于它能完整地表示高维数据，且能维持高维空间数据的本征结构信息，具有提高数据统计特性及改善数据稀疏性等优点[14].因此，本节拟采用张量分解中的高阶奇异值分解(high-order singular value decomposition，HOSVD)方法对由时间感知用户-主题分布构成的张量进行分解，得到稠密的预测张量，以实现更为准确的推荐.

3.1UZT模型

首先，构建初始三阶初始评分张量Y∈N×K×O，其中N为用户数，K为主题数，O为时间片数，如图5所示：

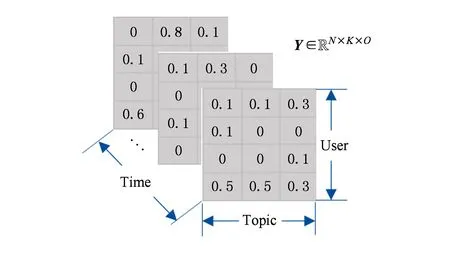
Fig. 5 User-topic-time 3-order original tensor图5 用户-主题-时间三阶初始张量

Y中的每个元素Yn kt表示第n个用户在时间段t对第k个主题的兴趣评分(preferencerating,PR)：

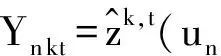
该三阶张量为稀疏矩阵，不能反映用户对全部主题的兴趣.本文采用高阶奇异值分解方法获取稠密张量，该方法是以多元线性代数为基础的奇异值泛化分解方法，用于解决多维数据的降维问题，基本步骤为

1) 将三阶张量分解成为用户U∈N×dU、主题Z∈K×dZ和时间T∈O×dT三个因子矩阵；

2) 构建核心张量G∈dU×dZ×dT，用于控制用户、主题、时间各因子矩阵之间的交互；

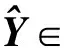
其中，“×U”表示张量和矩阵按照U-mode展开形式进行相乘，下标U表示了张量乘以矩阵的方向.“×Z”和“×T”同理.

3.2模型训练求解

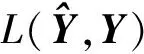
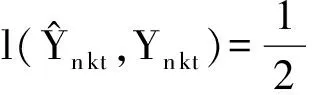
为避免过度拟合，将与U，Z，T，G相关的正则化引入到式(8)中，即添加这些因子F范数的正规则项，得到目标函数为

其中，λ和λG都为正则化参数.

运用简单在线算法的同时对因子矩阵Un*,Mk*,Tt*和核心张量G进行迭代，采取子空间随机梯度下降法(stochasticgradientdescent，SGD)将目标函数最小化.每个因子矩阵以及核心张量的迭代过程如下：

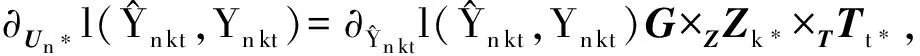
用户-主题-时间张量分解算法(简称为UZT)如算法2所示：

算法2. UZT算法.

输入：用户-主题-时间初始稀疏张量Y；

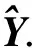
用较小的随机值初始化U∈K×dU，Z∈K×dZ，T∈O×dT，G∈dU×dZ×dT；

设置步长η；

while(n,k,t)in观察Ydo

endwhile

由于每次只访问矩阵U，Z，T中的1行数据，所以该算法比较容易实现，其时间复杂度为O(dU×dZ×dT×r)，其中dU，dZ，dT分别为张量分解3个因子矩阵的维度，r为迭代次数.

3.3POI得分转换及推荐

在进行POI推荐时，需将用户对主题的兴趣得分转换为对POI的兴趣得分.

根据得出的POI-主题矩阵，结合用户在特定时间下的主题兴趣分布(用户-时间-主题张量)，可计算用户在特定时间下对于具体POI的兴趣分布(用户-时间-POI).具体步骤为:

1) 采用K维向量P表示用户在特定时间段对于所有主题的兴趣得分，其中pk表示该用户对于主题k的兴趣偏好最终得分，即n和t固定时Yn kt的取值Yn:t；

2) 采用M×K维矩阵Q表示POI-主题分布，其中qmk表示主题k在兴趣点m中所占的比重.将K维向量与M×K的转置矩阵进行相乘，得到M维向量F，即用户在时间t对于全部兴趣点的兴趣得分.

(un,t):F=P×QT.

若fm为F中的元素，表示用户un在时间t对于兴趣点lm的兴趣得分：

(un,t):fm=pk×qmk.

于是，根据每个用户的POI得分向量F，选择得分最高的前N个兴趣点进行推荐.

4 实验与结果分析

本节通过在真实数据集上进行测试，验证所提出推荐策略的性能.

4.1实验数据集及评价指标

1) 数据集

实验采用来自Twitter提供的WW(world-wide)真实数据集，时间区域从2012-11-01—2013-02-13.

该数据集为“用户签到数据文档”，每一行包含用户编号、POI编号、POI经纬度、签到时间和评价信息5个属性.数据集共包含74 938条签到记录，其中包含3 883个用户和49 357个兴趣点.我们将其分为训练集和测试集2部分，其中训练集包含2012-11-01—2013-01-31数据，测试集包含从2013-02-01—2013-02-13的数据.

2) 评价指标

性能评价指标选用准确率、召回率和平均准确率(mean average precision,MAP)，分别用PRE@N，REC@N，MAP表示，其中N为推荐的POI数量.

准确率和召回率只是对返回POI推荐列表的正确性进行度量，而未考虑正确结果在推荐列表中的位置，即正确POI只要在推荐列表中出现就认为推荐正确;而评价指标MAP则是对准确率的进一步精准度量,该指标除考虑推荐结果的正确性之外，还考虑推荐正确的POI在推荐列表中的位置,若正确推荐结果在推荐列表中的位置越靠前，则MAP值就越高.

给定用户u，在时间片段t下的准确率PRE@N(t)、召回率REC@N(t)和MAP(t)的计算如式(15)所示：

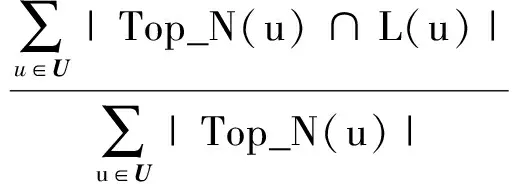
其中，Top_N(u)代表算法获取的Top-N兴趣点推荐列表;L(u)代表用户测试集中用户去过的兴趣点列表;Top_N(u)∩L(u)代表Top-N推荐列表和测试集列表的交集，即正确推荐列表;locn(Top_N(u)∩L(u))代表在Top-N列表中第n个兴趣点在推荐正确列表中的位置值.注意，在Top-N列表中但不在推荐正确列表中的locn(Top_N(u)∩L(u))=0.

整个算法的各项评价指标是所有时间段中各项指标的平均值.本文选取3种相关POI推荐算法进行比较：基于签到信息的矩阵分解法(CMF)[9],主题及位置感知法(TLA)[5]和用户-位置-时间张量分解法(ULT)[14].

4.2实验结果及分析

1) 主题个数对推荐结果的影响

在LDA模型中，主题个数K的选择直接影响到提取的主题结构.然而，选择最佳主题数仍然是其面临的主要难题[24].已有一些非参数主题模型提出，即主题个数随文档数目的变化而相应调整，而无需事先人为指定.但是，这些模型大都较为复杂，且效果也不理想.目前常用的方法是通过设置不同的K值，训练后验证比较求得主题个数的最佳值.

本实验分别取K=40，60，80，100，120时，验证UZT算法的性能，结果如图6所示.可以看出，对于本文的数据集，当K=100时，其准确率、召回率及平均准确率均高于其他值.因此主题个数不是越大越好，而要根据原始数据集所表现的特征确定.后续设置实验的主题个数K=100.

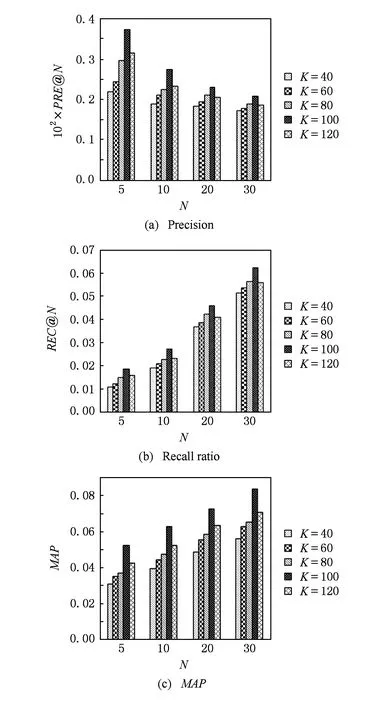
Fig. 6 POI recommendation performance on different numbers of topics图6 不同主题个数下的兴趣点推荐效果

2) 张量分解秩对推荐的影响

张量分解3个矩阵的秩参数，即核心张量的维度，决定了张量分解中潜在特征因素的数目.对于张量秩的确定，目前还没有方法能够直接求解任意给定张量的秩，已被证明是一个NP难问题[25].因此，本实验通过设定不同值，比较后求得秩的最优值.

在本文数据集中，原始张量维度为3883×24×100，设置其分解的秩为其维度的20%，40%，60%，80%，100%.实验结果如图7所示.可以看出，维度在60%时的性能优于其余4种，故本研究将秩设置为原始张量的60%.

Fig. 7 POI recommendation performance on different ranks of tensor图7 不同秩下的张量分解的兴趣点推荐效果

3) 不同推荐算法对比结果

基于上述实验参数，将所提出的UZT算法与所选择的3种算法进行实验对比，实验结果如图8所示.可以看出，UZT算法性能均优于其余算法.这是由于ULT只考虑了用户的签到次数，未考虑评论信息及用户的主题权重；TLA方法虽然考虑了用户-主题分布，但未考虑用户兴趣的时间感知特征，即认为所有时间的兴趣相同；CMF方法只能处理二维数据，计算得到的用户偏好准确度较低.

4) 时间粒度对推荐效果的影响

本研究是将签到数据按“小时(hour)”划分到24个时间片段中，然后按照时间点落在对应时段中推荐.

用户签到习惯往往具有一定规律性，因此，在不同时间表现出来的兴趣偏好可能不同.例如，用户在上午、下午和晚上的签到习惯不同,周一至周五(周工作日)的签到习惯与周六、周日(周末)的签到习惯也不相同.因此，我们将时间粒度进行扩展：

① 针对每天不同时间段用户的签到习惯可能不同，将全部签到数据按“时间段(section)”划分，即划分为6个时间段(每个时间段为4 h)：[6:00—10:00)，[10:00—14:00)，[14:00—18:00)，[18:00—22:00)，[22:00—2:00)，[2:00—6:00).

② 针对每周内每天用户的签到习惯可能不同，将全部签到数据按“周天(day of week)”进行划分，即按周一至周日划分为7个时间段.

③ 针对每月内每天用户的签到习惯可能不同，将全部签到数据按“月天(day of month)”进行划分，即划分为30个时间段.

图9的实验结果表明，时间粒度划分得越细，就能够获取更为准确的用户偏好，也就能得到更为准确的推荐结果.

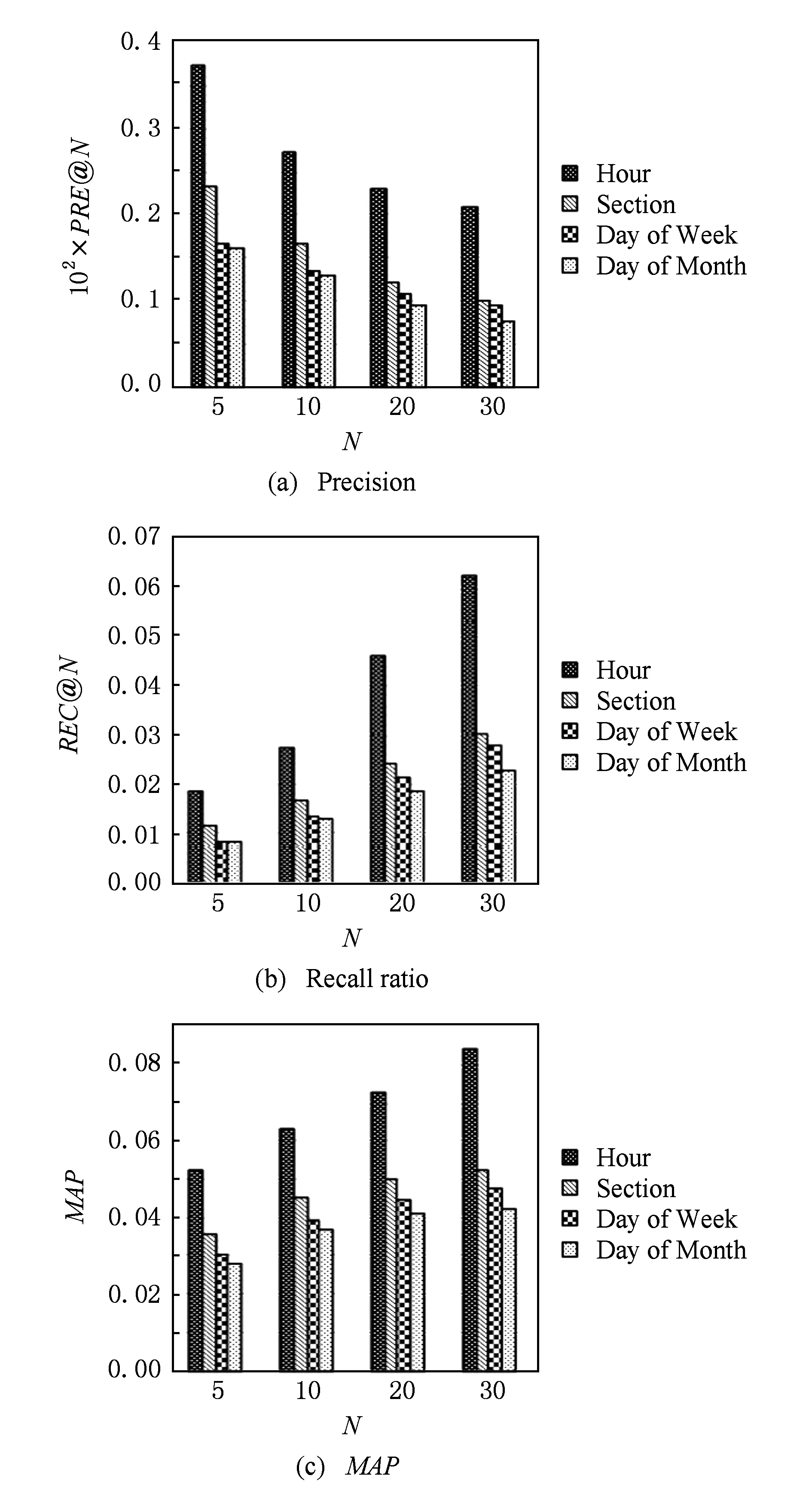
Fig. 9 POI recommendation performance on time granularity图9 时间粒度对兴趣点推荐效果的影响

5 全文总结

本文针对基于位置社会网络提出了一种双重细粒度POI推荐策略，即将时间划分为“小时”粒度，POI划分为“主题”粒度，以获取更为准确的用户偏好，从而能实现时间感知的POI推荐.

论文的主要工作包括2部分：利用LDA主题提取模型提取出POI-主题分布，并将其映射为时间感知的用户-主题偏好分布.为解决数据稀疏性问题，运用张量分解算法对得到的初始用户-主题-时间三阶张量进行分解，以获取更为准确的主题兴趣评分，从而实现POI的Top-N推荐.实验结果表明，本文所提算法具有较好性能.

本文所研究的时间感知推荐策略是将时间划分为离散的24个小时进行推荐，未能反映兴趣变化的连续性.因此，下一步我们将研究连续时间感知策略，进一步提高推荐准确率.

[1]Bobadilla J, Ortega F, Hernando A, et al. Recommender systems survey[J]. Knowledge-Based Systems, 2013, 46(1): 109-132[2]Gao Huiji, Liu Huan. Data analysis on location-based social networks[G]Mobile Social Networking. Berlin: Springer, 2014: 165-194

[3]Bao Jie, Zheng Yu, Wilkie D, et al. Recommendations in location-based social networks: A survey[J]. GeoInformatica, 2015, 19(3): 525-565

[4]Gao Huiji, Tang Jiliang, Hu Xia, et al. Content-aware point of interest recommendation on location-based social networks[C]Proc of the 29th Int AAAI Conf. Menlo Park, CA: AAAI, 2015: 1721-1727

[5]Liu Bin, Xiong Hui. Point-of-interest recommendation in location based social networks with topic and location awareness[C]Proc of the 13th SIAM Int Conf on Data Mining. Philadelphia, PA: SIAM, 2013: 396-404

[6]Ference G, Ye M, Lee W C. Location recommendation for out-of-town users in location-based social networks[C]Proc of the 22nd ACM Int Conf on Information amp; Knowledge Management. New York: ACM, 2013: 721-726

[7]Gao Huiji, Tang Jiliang, Liu Huan. Exploring social-historical ties on location-based social networks[C]Proc of the 6th Int AAAI Conf on Weblogs and Social Media. Menlo Park, CA: AAAI, 2012: 114-121

[8]Yuan Quan, Cong Gao, Ma Zongyang, et al. Time-aware point-of-interest recommendation[C]Proc of the 36th Int ACM SIGIR Conf on Research and Development in Information Retrieval. New York: ACM, 2013: 363-372

[9]Gao Huiji, Tang Jiliang, Hu Xia, et al. Exploring temporal effects for location recommendation on location-based social networks[C]Proc of the 7th Int ACM Conf on Recommender Systems. New York: ACM, 2013: 93-100

[10]Yuan Quan, Cong Gao, Sun Aixin. Graph-based point-of-interest recommendation with geographical and temporal influences[C]Proc of the 23rd Int ACM Conf on Conf on Information and Knowledge Management. New York: ACM, 2014: 659-668

[11]Ye Mao, Yin Peifeng, Lee Wang-Chien, et al. Exploiting geographical influence for collaborative point-of-interest recommendation[C]Proc of the 34th Int ACM SIGIR Conf on Research and Development in Information Retrieval. New York: ACM, 2011: 325-334

[12]Liu Bin, Fu Yanjie, Yao Zijun, et al. Learning geographical preferences for point-of-interest recommendation[C]Proc of the 19th Int ACM SIGKDD Conf on Knowledge Discovery and Data Mining. New York: ACM, 2013: 1043-1051

[13]Cheng Chen, Yang Haiqin, King I, et al. Fused matrix factorization with geographical and social influence in location-based social networks[C]Proc of the 26th Int AAAI Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2012: 17-23

[14]Yao Lina, Sheng Quanzheng, Qin Yongrui, et al. Context-aware point-of-interest recommendation using tensor factorization with social regularization[C]Proc of the 38th Int ACM SIGIR Conf on Research and Development in Information Retrieval. New York: ACM, 2015: 1007-1010

[15]Bao Jie, Zheng Yu, Mokbel M F. Location-based and preference-aware recommendation using sparse geo-social networking data[C]Proc of the 20th Int Conf on Advances in Geographic Information Systems. New York: ACM, 2012: 199-208

[16]Noulas A, Scellato S, Lathia N, et al. Mining user mobility features for next place prediction in location-based services[C]Proc of the 12th Int Conf on Data Mining. Piscataway, NJ: IEEE, 2012: 1038-1043

[17]Noulas A, Scellato S, Mascolo C, et al. An empirical study of geographic user activity patterns in foursquare[C]Proc of 5th Int AAAI Conf on Weblogs and Social Media (ICWSM). Menlo Park, CA: AAAI, 2011: 570-573

[18]Li Xutao, Cong Gao, Li Xiao Li, et al. Rank-GeoFM: A ranking based geographical factorization method for point of interest recommendation[C]Proc of the 38th Int ACM SIGIR Conf on Research and Development in Information Retrieval. New York: ACM, 2015: 433-442

[19]Gao Huij, Tang Jiliang, Hu Xia, et al. Modeling temporal effects of human mobile behavior on location-based social networks[C]Proc of the 22nd Int ACM Conf on Information amp; Knowledge Management. New York: ACM, 2013: 1673-1678

[20]Ifada N, Nayak R. Tensor-based item recommendation using probabilistic ranking in social tagging systems[C]Proc of the 23rd Int Conf on World Wide Web. New York: ACM, 2014: 805-810

[21]Yuan Q, Cong G, Ma Z, et al. Who, where, when and what: Discover spatio-temporal topics for Twitter users[C]Proc of the 19th Int ACM SIGKDD Conf on Knowledge Discovery and Data Mining. New York: ACM, 2013: 605-613

[22]Liu Bin, Xiong Hui, Papadimitriou S, et al. A general geographical probabilistic factor model for point of interest recommendation[J]. IEEE Trans on Knowledge and Data Engineering, 2015, 27(5): 1167-1179

[23]Cao Jiuxin, Dong Yi, Yang Pengwei, et al. POI recommendation based on meta-path in LBSN[J]. Chinese Journal of Computers, 2016, 39(4): 676-684 (in Chinese)(曹玖新, 董羿, 杨鹏伟, 等. LBSN中基于元路径的兴趣点推荐[J]. 计算机学报, 2016, 39(4): 676-684)

[24]Cao Juan, Zhang Yongdong, Li Jintao, et al. A method of adaptively selecting best LDA model based on density[J]. Chinese Journal of Computers, 2008, 31(10): 1780-1787 (in Chinese)(曹娟, 张勇东, 李锦涛, 等. 一种基于密度的自适应最优LDA模型选择方法[J]. 计算机学报, 2008, 31(10): 1780-1787)

[25]Anandkumar A, Ge R, Hsu D, et al. Tensor decompositions for learning latent variable models[J]. Journal of Machine Learning Research, 2014, 15(1): 2773-2832

LiaoGuoqiong, born in 1969. PhD. Professor and PhD supervisor at the School of Information Technology, Jiangxi University of Finance and Economics. Senior member of CCF. His main research interests include databases, data mining and social networks.

JiangShan, born in 1991. Master candidate at the School of Information Technology, Jiangxi University of Finance and Economics. Her main research interests include data mining and social networks.

ZhouZhiheng, born in 1993. Master candidate at the School of Information Technology, Jiangxi University of Finance and Economics. His main research interests include data mining and social networks.

WanChangxuan, born in 1962. PhD. Professor and PhD supervisor at the School of Information Technology, Jiangxi University of Finance and Economics. Senior member of CCF. His main research interests include Web data management and Web information retrieval.

DualFine-GranularityPOIRecommendationonLocation-BasedSocialNetworks

Liao Guoqiong1,2, Jiang Shan1, Zhou Zhiheng1, and Wan Changxuan1,2

1(School of Information Technology, Jiangxi University of Finance and Economics, Nanchang 330013)2(Jiangxi Province Key Laboratory of Data and Knowledge Engineering (Jiangxi University of Finance and Economics), Nanchang 330013)

Point of interest recommendation is a new form of popular recommendation in location-based social network (LBSN). Utilizing the rich information contained in the LBSN to do personalized recommendation can enhance user experience effectively and enhance user’s dependence on LBSN. Facing the challenging problems in LBSN, such as no explicit user preferences, non-consistency of interest, the sparseness of data, and so on, a dual fine-granularity POI recommendation strategy is proposed, of which, on the one hand, the historical check-in information of each user is divided into 24 time periods in hours; on the other hand, each POI is divided into a number of potential topics and distribution. Both the information of user’s check-in and comments are used to mine user’s topic preference in different time periods for Top-Nrecommendation of the POIs. In order to achieve the recommendation ideas, first of all, according to the comments information on the visited POIs, we use LDA topic generation model to extract the topic distribution of each POI. Secondly, for each user, we divide each user’s check-in data into 24 time periods, and connect it with the topic distribution of the corresponding POIs to map user interest preference on each topic in different periods. Finally, in order to solve the issue of data sparse, we use higher order singular value decomposition algorithm to decompose the third-order tensor of user-topic-time to get more accurate interest score of users on each topic in all time periods. The experiments on a real dataset show that the proposed approach outperforms the state-of-the-art POI recommendation methods.

POI recommendation; location-based social network (LBSN); LDA topic model; interest mapping; tensor factorization

2016-07-11；

2016-12-15

国家自然科学基金项目(61772245,61262009)；江西省自然科学基金项目(20151122040083)；江西省优势科技创新团队建设计划项目(20113BCB24008)；江西省教育厅重点科技项目(GJJ160419)

This work was supported by the National Natural Science Foundation of China (61772245,61262009), the Natural Science Foundation of Jiangxi Province of China (20151122040083), the Superiority Science and Technology Innovation Team Building Program of Jiangxi Province (20113BCB24008), and the Science Foundation of Jiangxi Provincial Department of Education of China (GJJ160419).

(liaoguoqiong@163.com)

TP181