基于贝叶斯参数估计的期货市场交易成本、流动性与资产定价研究
2017-12-08刘志东
刘志东,姜 玲
中央财经大学 管理科学与工程学院,北京 100081
基于贝叶斯参数估计的期货市场交易成本、流动性与资产定价研究
刘志东,姜 玲
中央财经大学 管理科学与工程学院,北京 100081
近年来交易成本和流动性对于股票资产的预期收益或定价影响受到学术界和业界的关注,期货市场的各种交易产生大量数据,这些数据中隐藏着重要的信息,但采用逐笔高频交易数据对期货市场交易成本、流动性和资产定价问题进行系统研究的比较少,对期货市场交易成本和流动性的内涵、特征、度量方法,以及交易成本和流动性在期货资产定价中的作用等问题有待深入探讨。
从序贯交易模型的视角,基于贝叶斯参数估计方法及逐笔高频交易数据和每日收盘价格数据测量期货市场的交易成本,对不同交易成本和流动性测量方法进行比较研究,探讨各种交易成本与流动性的相互关系,选出合适的流动性测量方法。同时,从逐笔高频交易数据存在报价离散化、价格聚集和非对称信息等方面对交易成本模型修正和扩展。将交易成本与真实收益率结合并考虑市场规模和周内效应的作用,构建期货市场资产定价模型,从中国期货市场选取不同品种的主力合约数据进行实证研究。
研究结果表明,基于贝叶斯参数估计和逐笔高频交易数据的交易成本的测量方法具有明显的优点,可以克服传统基于矩估计交易成本测量交易成本的不足,更适合用来作为流动性的代理变量。①订单对价格存在比较显著的冲击现象,这些冲击表明私人信息被包含在这些合约的交易里。②基于完整模型的交易成本更适合用来作为流动性的代理变量,与定义法的流行性成本估计值的相关系数更高,基于逐笔高频交易数据和完整模型的交易成本是最优的流动性的代理变量。③交易成本确实被包含在超额收益中,总体来说,交易成本对资产收益率的影响具有比较明显的周内效应。因此,流动性对投资期货的收益率有很大贡献,为了达到更高的收益,通常需要为获得好的流动性而付出更高的代价。
从序贯交易模型的视角,基于贝叶斯参数估计方法和逐笔高频交易数据测量期货市场的交易成本,有助于市场参与主体更好地认识和分析期货市场的交易成本、流动性和资产收益之间的关系,对市场监管机构有效评估市场质量、设计合理的期货市场交易制度、有效降低市场交易者的交易成本、增强期货市场流动性、提高市场运行效率具有一定的参考价值。
交易成本;流动性;资产定价;贝叶斯参数估计;高频交易数据
引言
交易成本和流动性是衡量金融市场运行效率和成熟程度的重要指标。对于期货市场来说,保持期货市场良好的流动性,降低交易成本,不仅可以发挥价格发现的功能,而且有利于设计合理的交易策略,降低交易者面临的风险。交易成本包括显性成本和隐性成本,显性成本即为手续费、佣金和交易税等,隐性成本包括由于订单交易引起的价格变化、机会成本和不能及时成交的延迟成本等。显性成本比较好测量,一般经纪人或者做市商都会给出详细的报告说明,而隐性成本比较难测算。在简单的限价交易中,交易成本可以用成交价格与买卖报价的中值的差进行衡量。但是,由于计算机和通信技术水平的限制,对于交易数据的记录并不准确。所以,需要找到其他的代理变量衡量交易成本。
对于期货市场而言,流动性对期货市场有重要意义,流动性越好资源配置效率就越高。只有当市场具有足够的流动性时,期货市场才能为投资者提供交易的机会,各种交易才能顺利完成。尽管流动性是衡量期货市场运行效率的主要指标,但流动性是一个十分抽象的概念,如何对其进行定量一直备受关注,其中最困难的当属如何选取和设计流动性指标。
近年来交易成本和流动性对于股票资产的预期收益或定价的影响受到学术界和业界的关注,但对交易成本和流动性对期货资产收益的影响进行系统研究的不多,而且没有得出一致的结论。因此,有必要从市场微观结构和资产定价角度构建模型,对期货市场交易成本、流动性和资产定价问题进行系统研究,分析交易成本是否作为一个因子在期货价格中被定价。
1 相关研究评述
关于金融市场的交易成本问题,PEROLD[1]最先提出成交差价的概念,认为成交差价是交易者与市场进行交流的隐性成本,是成交价格与理想价格的差值。投资科技集团(investment technology group,ITG)用成交差价与佣金之和计算交易成本。HASBROUCK[2]认为,交易成本是实际成交价格与理想价格之间的差值。即当我们做出投资决定时,对资产进行评估后得到一个理想价格,而实际成交价格往往会高于这个理想价格,这个差值就归于交易成本。对于理想价格,不同的机构有不同的定义,美国证券交易委员会定义为成交前最佳买卖报价(national best bid and offer,NBBO)的中间价。
在最简单的序贯交易模型中,市场中一个处于买家位置的交易者通过满足报价者设定的报价来达成立即成交,这里交易成本指为满足流动性而付出的成本,也即流动性成本。在复杂的序贯交易中,交易成本不仅包含流动性成本。但是,剔除机会成本等,交易成本从狭义角度看绝大部分是与市场流动性有关。对于市场流动性,国际清算银行给出了比较全面的定义,认为市场流动性是能够使市场参与者迅速进行大量交易且不会引起金融资产价格产生大幅波动的一种市场特征。如果市场流动性充足,交易者就可以比较低的价格迅速达成交易,也即市场应该具有比较快的指令执行速度和比较低的交易成本。从这个定义上看,交易成本可以衡量市场的流动性,交易成本可以作为一个流动性的代理变量,概念易于理解,具有很强的实用性。因此,本研究探讨的交易成本是指隐性交易成本,作为流动性的测量指标。
交易成本和流动性的估计一直是金融微观市场结构重要的研究内容。ROLL[3]通过矩估计方法估计买卖差价;LAUX et al.[4]和MA et al.[5]基于交易层面数据,根据ROLL序贯交易模型,采用矩估计的方法研究市场交易成本和流动性。但是矩估计的方法存在明显的缺陷,即价格变动的协方差必须是负值才能够使用,所以矩估计的值会明显偏高。另外,他们使用的ROLL模型没有考虑信息对价格的影响。MANASTER et al.[6]和LOCKE et al.[7]使用计算机处理的交易重现(computerized trade reconstruction,CTR)数据重点研究持仓量与流动性之间的关系,使用CTR数据可以准确知道交易的方向。MANASTER et al.[6]还估计了订单对不同层次交易者的影响。HASBROUCK[8]基于逐笔交易和报价数据,根据ROLL序贯交易模型,采用贝叶斯参数估计中的Gibbs抽样技术,通过对带有交易发起方向的指令流的估计衡量期货市场流动性和交易成本。但是他并没有研究交易成本和流动性对期货收益的影响。HASBROUCK[2]为了克服1983年之前高频交易数据缺失的困难,基于美国芝加哥大学证券价格研究中心的每日股票价格收盘价数据,根据ROLL序贯交易模型,采用贝叶斯方法估计美国股票市场的交易成本和交易方向等,发现采用每日数据估计的交易成本和采用逐笔交易和报价数据估计的交易成本差别不大,并根据较长时间样本(1926-2006),发现在资产定价中考虑交易成本后,交易成本与股票收益具有正相关关系,这种正相关性在一月份最显著,具有明显的一月份效应。BLEANEY et al.[9]在交易方向已知的前提下,通过使被估计的买卖价差一半调整后的价格序列的协方差最大化来估计交易的买卖价差。但是该方法没有考虑交易与价格之间反馈效应,交易成本和流动性估计过程存在不足。AMIHUD et al.[10]对45个国家股票市场的非流动性溢价问题进行检验,发现在控制其他定价因子后,非流动性溢价显著为正;BLEANEY et al.[11]在非理想条件下对买卖价差估计的绩效进行研究;FONG et al.[12]的研究结果给出美国和国际上其他股票交易成本;MARSHALL et al.[13]对非流动订单流驱动市场中不同交易量下的交易成本问题进行研究,在综合考虑样本数据抽样频率、收益率波动率、交易方向、收益和交易之间的反馈效应后,通过仿真研究发现采用能获得的最高频数据估计买卖价差更准确。但是该研究没有考虑价格离散化和最小报价单位等微观市场结构的影响。GOYENKO et al.[14]以基于高频交易数据的已实现价差、有效价差、价格冲击等的流动性测量方法为基准,发现采用日度数据估计流动性效果更好;HOLDEN et al.[15]也采用日度交易数据测量流动性,发现估计流动性效果也更好。
CHORDIA et al.[16]、ANGEL et al.[17]和KIM et al.[18]对基于微小价差和较浅市场深度的高频交易数据度量流动性方法的精确度和可行性表示疑问;HOLDEN et al.[15]证明当已实现的美元价差很小和股票市场的深度很低时,价差不能完全捕捉到市场的流动性;EASLEY et al.[19]研究发现订单分割可以使连续不断的交易相互关联;DEUSKAR et al.[20]基于订单簿中的累计市场深度信息,提出一种流动性测量方法。但是在很多应用中,订单簿的信息很难完全得到,同时他们的方法也不能捕捉到订单分割对流动性的影响。关于流动性风险溢价方面的研究结论也不完全一致。BEN-REPHAEL et al.[21]使用每日观测数据研究发现,十进制报价之后并没有发现显著的流动性溢价;BOULATOV et al.[22]研究发现当隐藏订单不允许时,知情交易者偏好消耗流动性。上述关于流动性的研究存在的主要问题是采用统计指标不一定合理,同时没有全面考虑微观市场结构对流行性的影响。
中国学者卢斌等[23]对中国期货市场的流动性进行研究,发现从交易成本和交易对有效价格的影响系数这两个指标看,黄金期货的流动性最强;如果仅考虑交易成本单个指标,则强麦期货的流动性也较强。铜、铝、天然橡胶、大豆和强麦期货交易中含有大量有用的私有信息,信息不对称程度很高。但是该研究并没有对交易成本和流动性的各种测量指标进行系统比较,没有分析流动性和交易成本是否在中国期货市场得到定价。沈虹[24]从流动性成本、流动性波动和到期日3个角度构建衡量期货市场的综合流动性度量指标,并利用该指标对中国期货市场的流动性溢价问题进行研究,实证结果表明,流动性水平的差异对不同到期日期货合约的收益差异的影响存在差异性。但是该研究在构建流动指标时忽略很多交易信息,只是采用每日成交量、每日最高价格和最低价格。李泽海等[25]对中国期货合约流动性度量方法进行实证研究,考虑持仓量变化对期货合约流动性的影响,提出量仓比率模型,以同时反映期货合约的持仓量特征和交易量特征,实证表明量仓比率做为流动性度量方法,可以为期货市场交易管理和风险分析提供有效的技术手段。但是该研究以日度时间计算波动率代替最大价差带来的最大问题同样是忽略日内大量交易信息。刘向丽等[26]研究发现用价格变动和交易量衡量的流动性有冲突,构建基于久期的流动性比率指标描述市场流动性,用构建的新的流动性多维指标研究中国期货市场流动性的日内趋势及影响因素,实证结果表明交易量和持仓量对市场流动性都具有显著的正影响,绝对收益率对流动性有显著的负影响,且交易量比价格变动影响更为显著,分析表明国外常用的价差指标不适用于中国市场;史永东等[27]基于中国期货市场5分钟高频数据,对中国期货市场各板块间的风险传导效应进行研究,结果表明个别板块的波动显现出一定程度的周內效应;王硕等[28]建立指令驱动系统下的Easley-Kiefer-O′hara-Paperman模型,估计市场中的知情交易比例和不同信息状态下非知情交易者的异质期望衡量指标,并利用多因素模型回归研究异质期望与资产定价的关系。但基于指令驱动市场的EKOP模型的假设较为严格,资产交易或不交易的决策是相互独立的,这与现实市场中资产之间具有较强的相关性不完全一致。
随着计算机和通信技术的发展,期货市场的各种交易产生大量数据,这些数据中隐藏着重要的信息。但是由上述分析可以发现,采用逐笔高频交易数据对中国期货市场交易成本、流动性和资产定价问题的研究比较少,对期货市场交易成本和流动性的内涵、特征和度量方法,以及流动性和交易成本在期货资产定价中的作用等问题有待深入探讨。
从序贯交易的视角看,买卖双方先设定买卖报价,然后按照一定的规则成交,在任何一次成交之后,报价会被修正。这要求理想的序贯交易模型必须及时反映订单的方向,反映价格变动与订单流之间动态变化关系。但这样的模型对数据要求非常高,不仅要求成交的明细资料,还需要报价的高频交易数据。尽管在电子化交易时代,通过电子系统进行报价会有记录,但由于报价是瞬时完成的,其记录依然受限于技术原因,无法准确辨认买卖报价的先后顺序。通常我们可以获得逐笔的成交记录,这些记录只有在交易完成时才更新价格,只记录成交的瞬间买卖报价的情况,并不能确定买卖订单的先后顺序,因而也无法满足序贯交易模型的要求。同时,在现实中能获得的市场数据中存在很多隐藏的数据,如买卖报价,更重要的是订单的方向无法获得。由于在广义序贯交易模型中需要考虑交易发起的方向和资产有效价格等无法观测的变量,因此本研究借助Gibbs统计抽样方法,在贝叶斯统计的框架下对模型参数进行估计。
2 基本模型和贝叶斯参数估计
2.1ROLL模型
ROLL模型直接利用买卖报价,简单易于理解,本研究运用该模型。ROLL模型中有效价格的动态变化可以表示为
mt=mt-1+μt
mt=log(Mt)
(1)
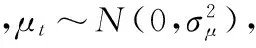
(2)
其中,at为买方报价;bt为卖方报价;c为买卖价差的一半,即为本研究中的交易成本,c>0。在本研究中,使用狭义的交易成本定义,将成交前的最佳买卖报价的中间价设为理想价格,成交价与理想价格的差即为交易成本。设qt为成交方向,qt∈{-1,+1},-1代表订单的方向为卖,+1代表订单的方向为买,满足伯努利随机分布,即买卖出现的概率是相等的。因此,交易价格可以表示为
(3)
pt=mt+cqt
(4)
其中,pt为交易价格。
可以得到
Δpt=mt+cqt-(mt-1+cqt-1)
=cΔqt+μt
(5)
根据(5)式,通过对样本值的方差和协方差的估计,就可以用广义矩估计的方法估计出参数c和σμ。
即
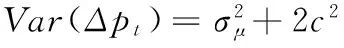
Cov(Δpt,Δpt-1)=-c2
(6)

(7)
广义矩估计方法比较容易实施,但从广义矩估计的表达式中可以明显看出该方法的不足。首先,只有当价格变化的协方差为负时才能使用广义矩估计方法。在美国证券市场上,ROLL[3]发现21个样本的日收益率中,大约有一半的协方差为正值。HARRIS[29]发现,在买卖价差较小时,更容易出现正的协方差。为弥补这个缺陷,当协方差为正值时,将估计值设定为0。其次,对于分笔数据,当某个时间没有交易时,通常会用前一个时间的买卖报价的中间值替代最新价格,这种价格中不包含交易成本,如果这种样本包括在矩估计的样本中,会使所估计的交易成本偏低,而如果把这些数据去掉,那么一个有效的价格可能会跨越几个时间点,这样会出现异方差性。
2.2贝叶斯参数估计方法和Gibbs抽样
贝叶斯统计推断以观察到的数据为基础,通过条件后验分布对参数和状态变量进行估计,其与传统估计方法最大不同在于,在贝叶斯方法中,参数被看成是随机变量而不是一个固定的值,先验分布包含了参数初始值的不确定性。运用贝叶斯方法进行参数估计包括构建以观察数据为条件的后验分布,这个后验分布包含了所有观察到的信息。更重要的是,贝叶斯方法在使用或处理观测不到的数据(即潜在变量)时比传统方法更适合。在序贯交易的视角下,对于订单方向的记录并不准确。在逐笔交易和报价数据中,只有价格和交易量是可观测的数据。在ROLL模型中,买卖报价和订单的方向都是潜在变量。传统估计方法不能很好利用含有潜在变量的样本数据,而在实际交易中,这些潜在变量都有经济学的意义。因此,贝叶斯方法更加适合序贯交易模型。

2.3关于成交方向的进一步考虑
在序贯交易模型中,订单的方向非常重要。但是目前只有在纽约交易所的TORQ(trade, order, report, quote)数据库中将成交与订单方向联系起来是有可能的,而在一般的数据库中成交方向都是通过相关的价格进行推断的,常见的方法就是通过成交之前最接近的价格判断成交的方向[30-31]。在缺乏报价数据的情况下,有一种貌似合理的方法是根据逐笔高频交易数据检测成交方向,把成交方向设为根据成交价格变动的固定值。当价格向上变化或者零变化时,令qt=+1;当价格向下变化或者零变化时,令qt=-1。即在模型中直接加入交易隐含的信息,在贝叶斯的框架中将qt设为由成交决定的固定的值,对c和σμ抽样。
2.4交易对价格暂时性的冲击
可以在模型中加入交易对有效价格的冲击,以此来反映交易中的信息,此时有效价格的动态过程可以表示为
mt=mt-1+qtVtλ+μt
(8)
其中,Vt为交易量,λ为交易对价格冲击或影响的系数,qtVt为有方向的交易量。ROLL模型的框架在这里与之前是一样的,即根据(4)式,Δpt=Δmt+cqt=λqtVt+cqt+μt。此时模型比之前复杂之处不仅在于多了一个参数λ,而且qt与mt之间相互依赖。由于篇幅限制,具体的抽样和推断过程在此省略,如有需要可以与作者联系。
2.5基本模型的运用
(1)样本构成及描述
将上述基本模型运用到中国期货市场,选取2014年7月中国期货市场3个交易所交易比较活跃的18个期货品种主力合约作为研究对象,这些合约分别为上海期货交易所的银(AG)、铝(AL)、热轧卷板(HC)、橡胶(RU)、锌(ZN)合约,大连商品交易所的鸡蛋(JD)、焦煤(JM)、聚乙烯(L)、豆粕(M)、聚氯乙烯(V),郑州商品交易所的棉花(CF)、玻璃(FG)、晚籼稻(LR)、甲醇(ME)、菜油(OI)、早籼稻(RI)、菜粕(RM)、强麦(WH)合约。数据的合约信息来自WIND资讯,逐笔成交数据来源于大富翁数据中心。由于篇幅限制,描述性统计表在此省略,如有需要可以与作者联系。从总交易笔数看,这些合约交易都比较活跃;从平均每笔成交间隔看,大部分品种的成交间隔都在1秒以内,除热轧卷板、聚氯乙烯、晚籼稻、强麦这几个品种,这几个品种的成交间隔也都在10秒以内,成交非常密集。基于序贯交易的视角,这样的成交过于密集,导致不止一个交易在一个时间窗格内,因此,对成交价格进行离散化处理很有必要。同时还统计了每笔交易成交量的分布情况。基于序贯交易的视角,成交量中包含私人信息,后续报价者通过观察之前的成交情况可以推测这些信息,进而修改之后的报价。
(2)贝叶斯基本模型逐笔数据的实证结果
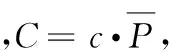
对比C与合约的最小变动价位,发现C的值比最小变动价位小得多,同时根据统计的平均每笔交易间隔时间的平均值显示的结果,对于逐笔高频交易数据,基于序贯交易的角度,需要对成交价格进行离散化处理。在上文,本研究还比较了使用贝叶斯参数估计方法与传统矩估计方法对波动率参数估计的结果,这两种方法波动率非常接近。但是,对交易成本的估计上,矩估计方法比贝叶斯参数方法相差很多。这样的现象可以归因于这两种方法对数据使用的方式不同。
同时在贝叶斯的框架中,将qt设为由成交决定的固定值,再利用贝叶斯分析框架进行Gibbs抽样估计参数。从计算结果可知,固定q与完全的贝叶斯估计在某些参数方面的估计值有所不同。固定q对交易成本的估计比完全的贝叶斯估计大很多,原因是根据成交价格变化而判断成交方向将太多的价格变化都归属到成交方向上。从经济学角度看,这种方法是不合适的,因为它让成交方向与噪声项之间产生联系,违背独立性的假设。然而,在序贯交易的视角下,前一次的成交方向与之后的报价乃至成交价格确实是有关系的。如此明显的价格上涨将会被认为是由于买的订单带来的,因此下面将针对这种缺陷对模型进行修正。
3 交易成本与流动性之间的关系
3.1方法和样本描述
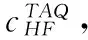
3.2各流动性代理变量相关性分析
采用逐笔交易数据计算每笔交易的交易成本,得到在每个交易日内每笔交易的平均交易成本。 根据119个合约样本和不同计算方法,对2014年各交易日每笔交易的平均交易成本进行相关性分析,统计结果见表2。
4 逐笔高频交易数据下基本模型的扩展
由表2相关性分析可知,使用贝叶斯方法和逐笔高频交易数据计算的交易成本是流动性的较好代理变量。但使用逐笔高频交易数据也面临一些问题,如非对称信息的影响、过度频繁的成交造成的价格集聚、序贯交易中订单流对价格的冲击等。通过对贝叶斯模型的运用,可以看到基本模型有两个明显的缺陷。①在交易方向的设定上,并没有分别对买卖的方向分开处理,没有对一个交易赋予一个单独的方向,而是对所有的交易方向赋予同一个概率分布,这样会让估计的过程产生与交易方向选择有关的误差。②交易方向和模型的参数联合起来进行估计,模型参数估计的不确定性会影响交易方向估计的不确定性。因此,本研究同时对上述基本模型进行扩展,使其更加符合实际交易的特征。

表1 各种流动性测量方法定义Table 1 Definition of Various Liquidity Measurement Method
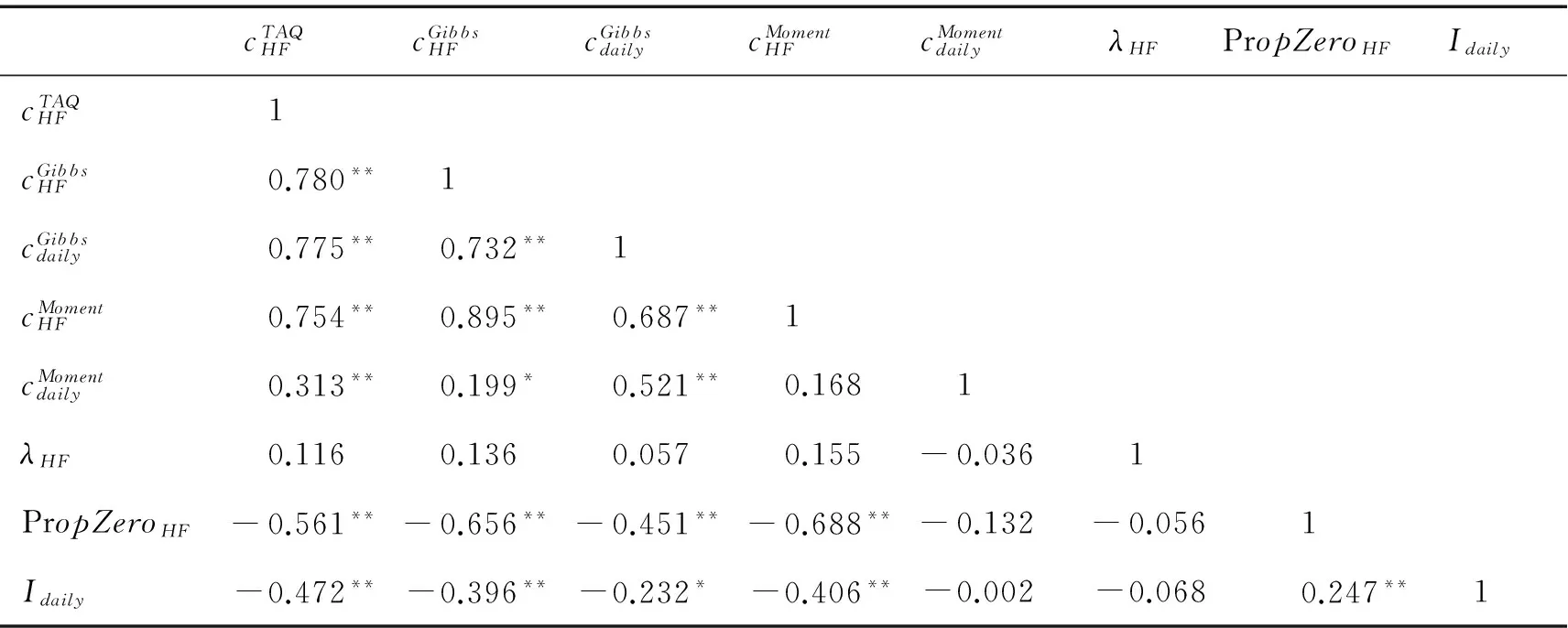
表2 流动性代理变量相关性分析结果Table 2 Results of Correlation Analysis between Liquidity Proxy Variables
注:**为显著性水平为0.050,*为显著性水平为0.100,下同。
4.1离散化处理
在本研究模型中,买卖报价和成交价格都被认为是连续型随机变量。但是事实上,几乎所有市场的买卖报价都是离散化的,买卖报价为最小报价单位整数倍的离散化数据。在经济学意义上最小报价单位与获得成交优先权所要付出的成本有关,对流动性有影响。从由数据主导的模型角度看,最小变动价位通常与价差以及短期内的价格变动很接近。HARRIS[33]提出含有潜在变量的模型对成交价格进行离散化;HASBROUCK[34]通过研究提出以下模型,即
At=Ceiling[Mt+C]
Bt=Floor[Mt-C]
(9)
其中,At为买方报价,At=exp(at);Bt为卖方报价,Bt=exp(bt);Mt为有效价格,Mt=exp(mt);Ceiling[·]为向上取整,Floor[·]为向下取整,通过这样的设定,每笔的报价都变为整数;在ROLL模型中,C被认为是最初交易人付出的成本,在这里对C的定义更加符合实际,即C为付给流动性提供者的成本,这种取整方法保证了每笔交易都涵盖这样的成本。因此,观察到的价格可以表示为
(10)
4.2聚集效应
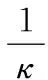

表3 过度的成交价格聚集/%Table 3 Excess Transaction Price Clustering/%
HASBROUCK[39]提出一种处理价格聚集的方式,将价格聚集归于一种隐形的交易成本,将最小价格变动单位的κ倍作为有效的价格变动单位,即为Kt,最小价格变动单位与交易惯例和个人偏好有关,考虑聚集效应,对报价进行处理,即
At=Ceiling[Mt+C,Kt]
Bt=Floor[Mt-C,Kt]
(11)
对于Kt,本研究考虑1和κ两个值。对此,可以对Kt假设一个独立同分布的伯努利分布,即
(12)

4.3交易对有效价格的影响
在上文对ROLL模型的阐述中,本研究假设有效价格与即将到来的订单的方向之间相互独立,即报价者从本次成交中获取不到任何信息。但是,序贯交易的一个特征就是有这样一种可能,即将到来的订单的方向反映着交易者的私人信息,然后报价者就可以通过观察这些订单推测这些私人信息,从而修改自己的报价。基于这样的观点,考虑滞后的影响,有效价格加入成交的影响后变为
(13)
其中,s为滞后时间,S为滞后期,λs为第s期交易对价格冲击或影响的系数。本研究可以获得准确的交易量数据,交易量同样会影响报价者对价格的修改。据此,对(8)式进一步扩展,即
(14)
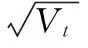
4.4扩展后完整模型的实证研究
将18个期货品种的主力合约数据运用到扩展后的总体模型中,分别得到18个合约的参数估计结果,由于篇幅限制,仅报告订单对价格冲击或影响系数λ,估计结果统计表在此省略,如有需要可以与作者联系。统计结果表明,除棉花期货、玻璃期货、晚籼稻期货、早籼稻期货外,其他λ值都是正的。成交对价格的冲击是一个累积的过程(如经过滞后的5笔成交),可以分为两部分。虽然对于大多数的合约来说,在第二次就显示了足够的影响。经过比较,上海期货交易所中,锌期货的价格受交易的影响最大,对热轧卷板期货的影响最小。大连商品交易所中,焦煤期货和聚氯乙烯期货的价格受的影响相对比较大,而对豆粕的影响比较小。郑州商品交易所中,影响系数出现了负值,且早籼稻期货的影响系数的绝对值很大,价格受交易冲击的幅度较大。
在经济学上,序贯交易模型能识别交易对价格的永久冲击中的非对称信息,私人信息通过交易的价格反映出来。基于这种观点,不难理解锌期货、焦煤期货、早籼稻期货,特别是早籼稻期货,为什么会有这么大的系数,对于早籼稻期货这种合约来说,订单冲击系数贡献了将近一半的波动率,除订单冲击外,基本没发现其他影响价格的证据。对3个交易所进行总体观察发现,大连的平均累积系数估计值最高(0.098),其次是上海(0.064),郑州的最小(0.001),说明总体来看,大连商品交易所更易于从订单流中进行价格发现,价格更容易受到交易的冲击。
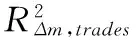
基于交易对价格的冲击是永久的而非暂时性的假设,本研究模型对此的设定存在一定的缺陷。本研究模型是一个短期模型,因而可能不能检测出超出5个滞后项的均值回复以及反转现象。其中,均值回复会表明交易对价格的冲击被夸大了。总体来说,对于交易成本(总体水平)的估计值比基本模型的估计值小。对此,一个简单的解释为,对买卖报价上下取整的修正作为隐藏变量加入模型,使C的后验分布总体更加靠近0,说明对于买卖报价的修正已经足够解释观察到的数据。而观察这3个交易所的交易成本,发现总的来说上海期货交易所的交易成本最高,最低的是郑州商品交易所。之前对数据统计也发现,上海期货交易所的平均每天成交笔数最大,其原因可能是上海期货交易所的交易更为活跃,换手率更高所带来的交易成本更高。
4.5修正前后估计值的比较
由上文可知,基于贝叶斯参数估计方法的逐笔高频交易数据估计值优于日内数据的估计值,且都优于其他的估计方法。在对模型修正后,在一定程度上去除了高频交易数据带来的问题。为了验证修正后的交易成本估计值是否能更好的作为流动性的代理变量,本研究沿用上一部分的思路,分别与定义法的流动性的估计值进行相关性比较。另外,在4.1~4.3部分考虑价格离散化、聚集效应和交易对有效价格影响的完整模型中,累积的交易对价格冲击系数也能衡量流动性,在此本研究也将它作为分析流动性的指标。
(1)样本描述和变量定义
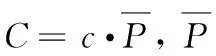
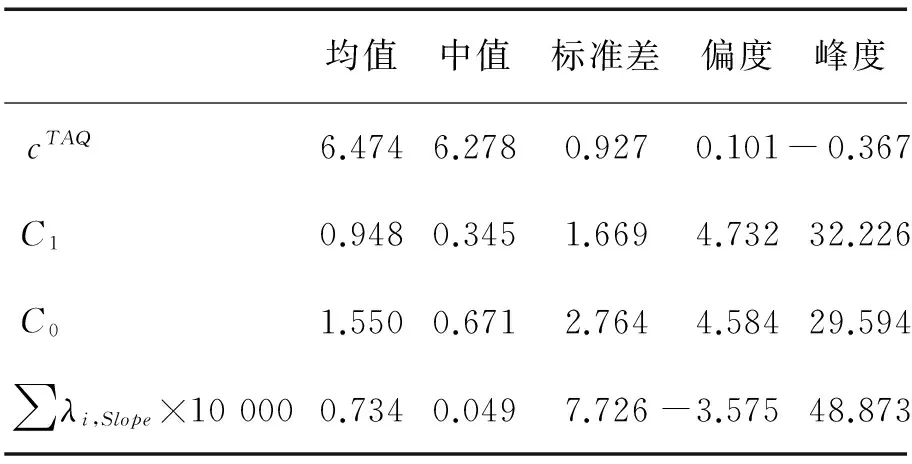
表4 变量描述性统计结果Table 4 Results of Variables Description Statistics
(2)相关性分析
利用表4描述的200个样本计算的4个变量的估计值进行相关性比较分析,结果见表5,表5给出标准的Person相关系数和Sperarman相关系数。由表5可知,完整模型和基本模型的交易成本的估计值都与定义法显著相关,完整模型估计值的相关系数为0.186,基本模型估计值的相关系数为0.097,完整模型的估计效果比基本模型的估计效果好。Spearman相关系数也显示同样的结果,分别为0.315和0.171。交易对价格的累积冲击系数,虽然Pearson相关系数不够显著,而Spearman相关系数还是很显著,但不如前两个变量的估计效果。原因可能是订单流的冲击带来的成本只是交易成本的一部分,不能完全概括流动性,因此,不能很好地作为流动性的代理变量。
5 期货收益率和交易成本
5.1实证分析方法
3.2和4.5中的实证研究表明,基于贝叶斯方法和高频交易数据计算的交易成本是较合适的流动性代理变量,下面对交易成本在期货资产定价中的作用进行实证研究,以分析交易成本是否作为一个因子在期货价格中被定价。尽管商品期货合约属于衍生品,但是其定价比金融资产和其他商品期货定价要复杂。基本的商品期货合约定价模型包括风险溢价模型和便利收益模型两类,基于多因素的风险溢价模型是通过统计方法,分析各种资产收益与风险的关系,风险的代理变量可以分为反映系统风险市场风险因子的代理变量和特征风险因子的代理变量。本研究实证分析方法采用多因素模型定价思想,加入特征风险因子,并应用于资产组合中。对于超额收益率,有

表5 模型扩展后各流动性代理变量相关性分析结果Table 5 Results of Correlation Analysis between Liquidity Proxy Variables after Model Modifications
注:对角线左下方数据为Pearson相关系数,对角线右上方数据为Spearman相关系数;***为显著性水平为0.010,下同。
Rw=α+βFw+δZw+εw
(15)
其中,w为时间,Rw为资产组合高于无风险收益率的超额收益率,α为常数项,Fw为市场风险因子的收益率,β为对市场风险因子的敏感系数,Zw为特征风险因子,δ为对特征风险因子的敏感系数,εw为噪声项。在(15)式中考虑了两类风险因子,第一部分是市场风险因子,即rm,w-rf,w,rm,w为中证商品指数每日的对数收益率,rf,w为Shibor隔夜拆借利率,在这里表示无风险利率;第二部分是特征因子,由本研究采用Gibbs方法估计出的交易成本C表示。对于市场规模以及与周内效应相关的因素影响处理如下,市场规模用持仓量代替,即资产组合内所有资产的持仓量(对数值)取平均,用MCw表示;周内效应用一个虚拟变量WeekDumw表示,并与交易成本和持仓量分别相乘,分析它们的交互作用。在回归时,分别将星期一至星期五代入进行分析。因此,定价模型变为
Rw=rw-rf,w
=δ0+βrm,w+δWeekWeekDumw+

δMC·Week(MCw·WeekDumw)+
δMC·-Week[MCw·(1-WeekDumw)]+εw
(16)
其中,rw为期货合约的每日收益率,cw为每日交易成本,δ0为常数项,δWeek为每日收益对周内某天效应的敏感系数,δc为每日收益对交易成本的敏感系数,δc·Week为每日收益对交易成本在周内某天效应的敏感系数,δc·-Week为每日收益对交易成本非周内某天效应的敏感系数,δMC·Week为每日收益对市场组合周内某天效应的敏感系数,δMC·-Week为每日收益对市场组合非周内某天效应的敏感系数。{}中上部和下部的表达式彼此独立,这样处理是为了避免多重共线性。
5.2资产组合样本构成及变量描述
从3个期货交易所中随机选出交易相对比较活跃的5个期货品中的主力合约作为样本,分别是上海期货交易所的银期货、铝期货、沥青期货、橡胶期货、锌期货,大连商品交易所的玉米期货、鸡蛋期货、焦煤期货、聚乙烯期货、豆粕期货,郑州商品交易所的棉花期货、玻璃期货、甲醇期货、菜油期货、早籼稻。使用2014年全年245天的逐笔交易数据进行研究,分别构造3个资产组合;收益率使用每个合约的每日收盘价计算的对数收益率,资产组合的收益率为组合内各品种的每日收益率以持仓量为权重进行的加权平均值,交易成本使用每日的逐笔交易数据计算,并进行加权平均得到组合的交易成本;持仓量为每日持仓量的对数值,组合的持仓量为组合内所有资产的持仓量的平均值;无风险收益率采用Shibor利率,市场风险收益率采用中证商品期货综合指数收益率。中证商品期货综合指数选取上市时间满一年的商品期货的所有合约,采用持仓量指标对所有合约的收盘价加权计算。3个资产组合各变量的描述性统计结果见表6。表6中,Cw为使用前文完整贝叶斯模型计算的每日交易成本,MCw为各资产每日持仓量的对数值。由表6统计结果可知,总体上郑州商品交易所内的合约交易成本较大,合约每日收益率也较低,上海期货交易所的合约交易成本较小,合约每日收益率也较高。其他变量与收益率之间的关系还不明显,需要通过模型进行详细分析。
5.3回归结果
将上述样本应用于(16)式资产定价模型,回归结果见表7、表8和表9。表7为2014年大连商品交易所5个期货品种主力合约的回归结果,第2列和第3列分别为不含常数项和含有常数项的一个风险因子的定价模型。结果显示,估计的市场风险的价格是1.154,t值为4.323;含有常数项的系数也非常显著,t值为8.822。符合定价模型的一般结论,市场风险对期货资产收益影响很大。第4列中加入流动性因子即交易成本,其系数为0.011,显著为正,t值为2.198。该结论符合我们的一般认知,资产定价时,其超额收益率中包含为获得流动性而付出的代价。第5列~第9列中引入代表星期一至星期五的虚拟变量,并且把交易成本的变量分割为含星期和不含星期两个部分。从回归结果看,星期三交易成本的系数为0.023,显著为正,t值为2.103;非星期三交易成本的系数为0.008,不显著,t值为1.383。因此,本研究推测,交易成本对收益率的影响有比较明显的周内效应,在星期三时对收益率的贡献尤其明显。第10列~第14列对交易成本对收益率的影响以及市场规模对收益率的影响分别考虑周内效应,回归结果显示,星期三交易成本的系数为0.021,显著为正,t值为1.937,与未加入市场规模因子时几乎没有发生变化,而市场规模因子的系数在星期三并不显著,为0.004,t值为0.656。反而在星期一时显著为正,系数为0.023,t值为3.114。因此,市场规模对收益率的影响也存在明显的周内效应,但是与交易成本的影响并不同步。
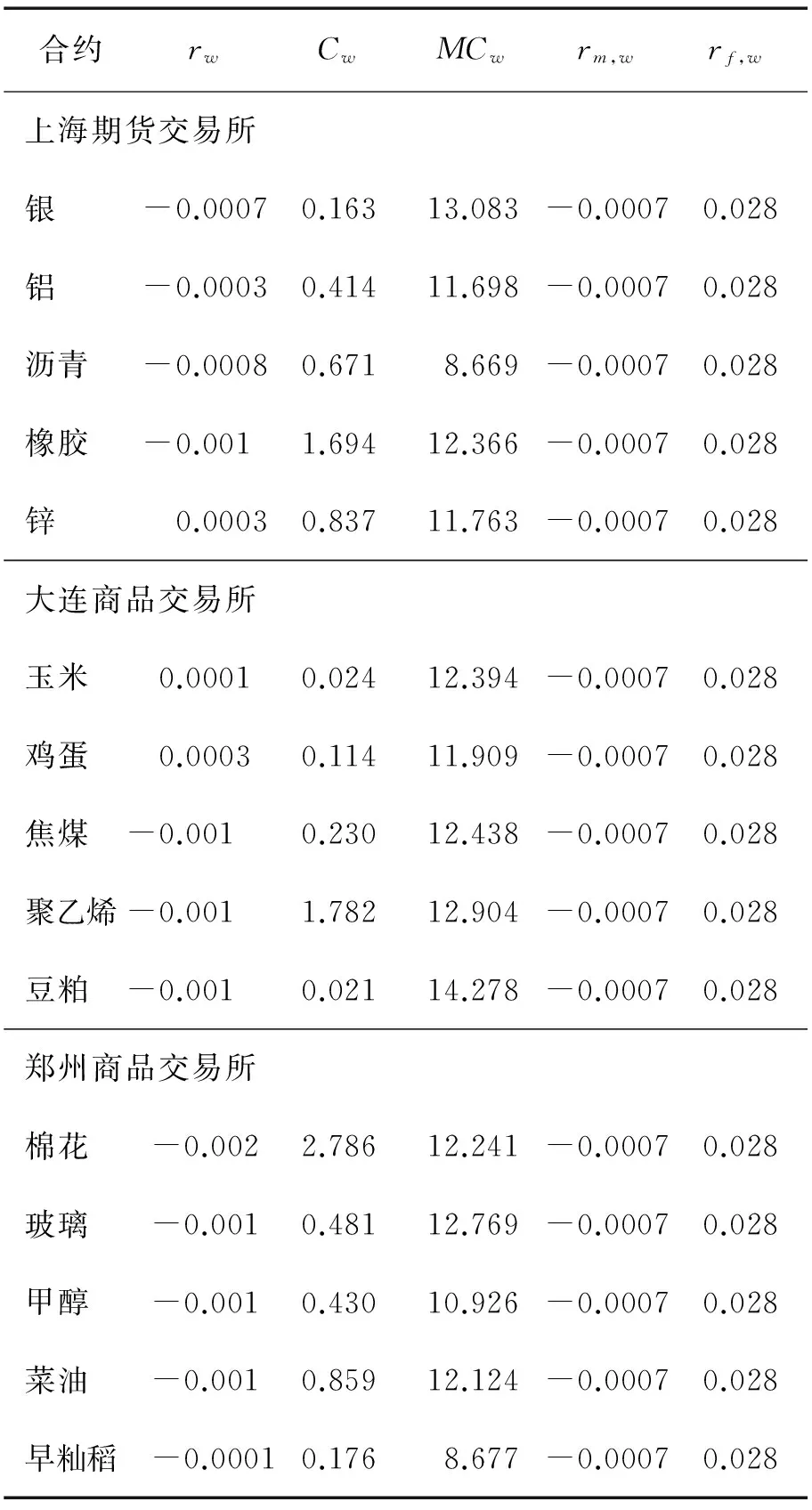
表6 资产组合变量描述性统计结果Table 6 Descriptive Statistics Results of Portfolio Variables
注:表中数据为用于回归的资产组合各资产对应指标的均值。
对于交易成本的星期三效应,可能的解释是,在每周的中间时,一般交易会比较活跃,买和卖的需求都处于一种拉锯的状态,因此,为了能够获得更加及时的交易,对流动性付出的代价会更高,同时及时成交所带来的超额收益也会更高。而对于持仓量的星期一效应可能来自于每周刚开始时,投资者会处于一种观望状态,此时比较容易出现投资的羊群效应,更倾向于投资市场规模比较大的合约,也因此,市场规模带来更高的收益。但是再之后,投资者对市场的分析渐趋理性,星期一效应逐渐消失。
表8和表9分别给出上海期货交易所和郑州商品交易所资产组合的回归结果。对这两个资产组合来说,由第2列和第3列可知,市场风险因子的系数都显著为正。由第4列结果可知,交易成本的系数并不如大连商品交易所的显著,其原因可能是由于这两个交易所(尤其是上海期货交易所)的换手率过高导致的。通过第一部分实证的样本也可以看到,上海期货交易所的交易比其他两个交易所交易要更加活跃,平均成交间隔更短,这从另一方面也表明上海期货交易所的换手率比较高,而换手率高带来交易成本过高,这就导致交易成本中代表流动性的部分相对减少,因此出现系数不显著或显著性低的情况。第5列~第9列的结果在各市场之间出现不同。上海交易所的资产组合并没有表现出明显的周内效应,而郑州商品交易所的资产组合的周内效应却出现在星期二,并且在加入代表市场规模的持仓量因子后,星期二的交易成本的系数变得更加显著。出现在星期二或星期三的原因应该大致相同,其都处于一周的中间位置,是买卖报价者的相互角力导致的结果。对于上海期货交易所,虽然其系数都不是特别显著,但是还是可以看到在星期二,交易成本的系数还是稍微有些显著的。出现这种情况的原因可能来自资产组合选取。
6 结论
本研究从序贯交易模型的视角,基于贝叶斯参数估计方法和逐笔高频交易数据测量期货市场的交易成本,对不同交易成本和流动性测量方法进行比较研究,探讨各种交易成本与流动性的相互关系,选出合适的流动性测量方法。同时,从逐笔高频交易数据存在报价离散化、价格聚集和非对称信息等方面对交易成本模型进行修正和扩展。将交易成本与真实收益率结合并考虑市场规模和周内效应的作用,构建期货市场资产定价模型,采用从中国期货市场所选的不同品种的主力合约数据进行研究,得到如下结果。
(1)订单对价格存在比较显著的冲击现象。特别是上海期货交易所和大连商品交易所的合约,冲击现象更加明显。如果订单冲击带来的是价格永久的变化,订单冲击对长期价格波动贡献了很大的一部分。这些冲击表明,私人信息正包含在这些合约的交易里。这与交易人群中潜在知情交易者的比例、当前交易者为知情交易者的概率有关,反映了投资者中的信息分布严重不对称,较小的交易量也会导致较大的价格变化,这些期货品种的流动性比较差,投资者的交易成本较大。但是,由于本研究模型是一个短期模型,只包含5个滞后项,缺乏检测均值回复和反转现象的能力,因此,可能会夸大这种订单冲击的影响。
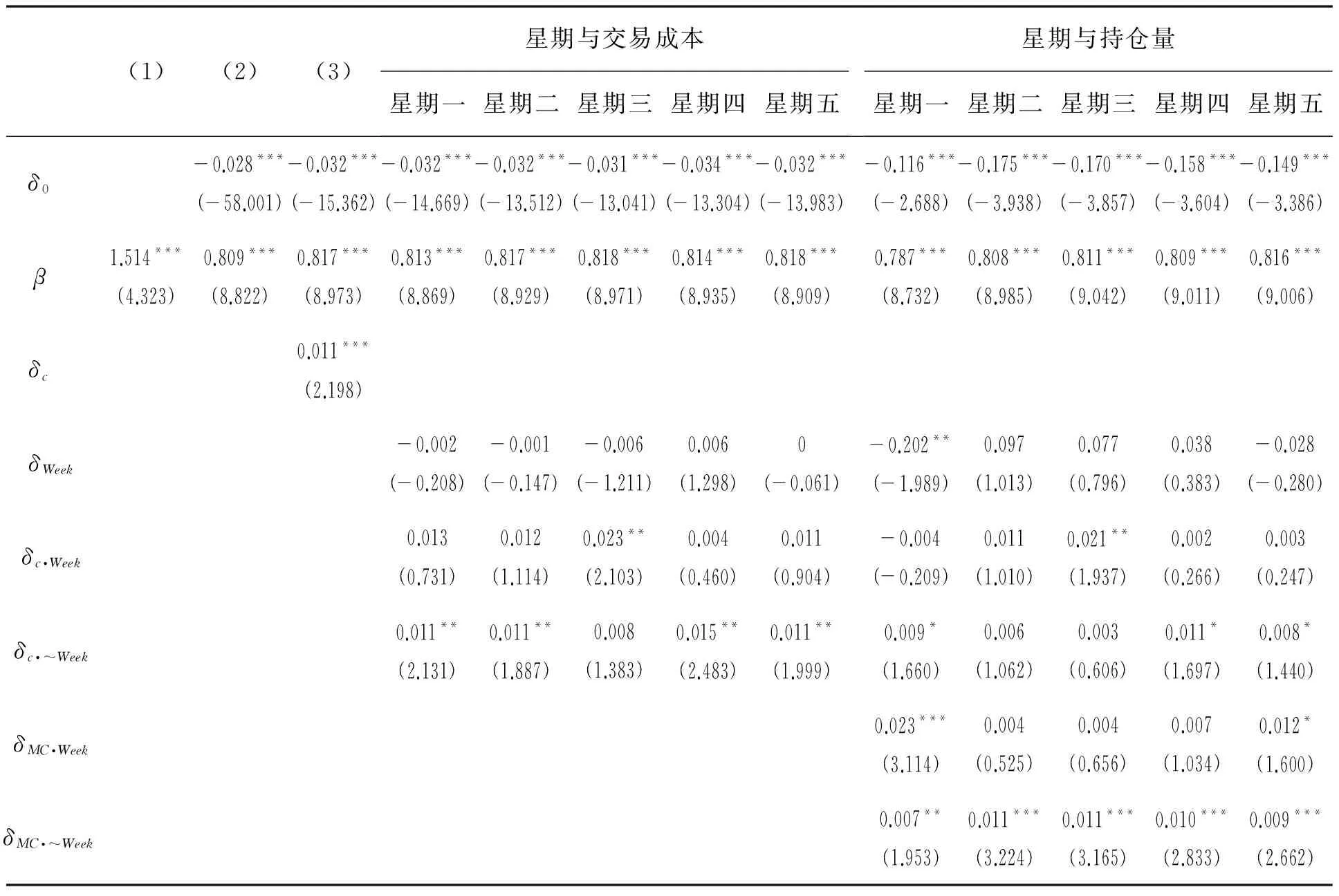
表7 大连商品交易所回归结果Table 7 Regression Results of Dalian Commodity Exchange
注:括号内数据为系数的t检验统计量,下同。

表8 上海期货交易所回归结果Table 8 Regression Results of Shanghai Futures Exchange

表9 郑州商品交易所回归结果Table 9 Regression Results of Zhengzhou Commodity Exchange
(2)本研究比较模型修改前和模型修改后对流动性估计的优劣,研究发现基于完整模型的交易成本更适合用来作为流动性的代理变量,与定义法的估计值的相关系数更高,基于逐笔高频交易数据和完整模型的交易成本是最优的流动性的代理变量。本研究还对中国期货市场交易成本和收益率问题进行探讨,发现交易成本确实被包含在超额收益中,总体来说,交易成本对资产收益率的影响具有比较明显的周内效应。因此,流动性对投资期货的收益率有很大贡献,为了达到更高的收益,通常需要为获得好的流动性而付出更高的代价。
(3)本研究发现交易成本比最小价格变动单位小得多。关于价格聚集现象,对比所选期货品种的主力合约,发现热轧卷板、棉花和豆粕的价格聚集最明显,其他品种的聚集都比较轻微。但是对于价格聚集的原因本研究并不能确定是因为便于协商价格还是因为市场的作用,这一问题有待将来深入研究。
综上,本研究认为,从序贯交易模型的视角,基于贝叶斯参数估计方法和逐笔高频交易数据测量期货市场的交易成本方法,有助于市场参与主体更好地认识和分析期货市场的交易成本、流动性和资产收益之间的关系,可以为市场监管机构有效评估市场质量、设计合理的期货市场交易制度、有效降低市场交易者的交易成本、增强期货市场流动性、提高市场运行效率具有一定的参考价值。
由于本研究采用逐笔高频交易数据和贝叶斯参数估计的模型计算量很大,并且中国期货市场逐笔高频交易数据库还不是非常完整,并没有在实证研究中使用时间更久的统一样本进行研究,有可能对实证结果有一定的影响。将来可通过提高模型计算效率以及扩大样本数据解决此问题,以便对中国期货市场数据中的信息进行更充分挖掘。
[1]PEROLD A F.The implementation shortfall:paper versus reality.TheJournalofPortfolioManagement,1988,14(3):4-9.
[2]HASBROUCK J.Trading costs and returns for U.S.equities:estimating effective costs from daily data.TheJournalofFinance,2009,64(3):1445-1477.
[3]ROLL R.A simple implicit measure of the effective bid-ask spread in an efficient market.TheJournalofFinance,1984,39(4):1127-1139.
[4]LAUX P A,SENCHACK,Jr A J.Bid-ask spreads in financial futures.TheJournalofFuturesMarkets,1992,12(6):621-634.
[5]MA C K,PETERSON R L,SEARS R S.Trading noise,adverse selection,and intraday bid-ask spreads in futures markets.TheJournalofFuturesMarkets,1992,12(5):519-538.
[6]MANASTER S,MANN S C.Life in the pits:competitive market making and inventory control.TheReviewofFinancialStudies,1996,9(3):953-975.
[7]LOCKE P R,VENKATESH P C.Futures market transaction costs.TheJournalofFuturesMarkets,1997,17(2):229-245.
[8]HASBROUCK J.Markov chain Monte Carlo algorithms for Bayesian estimation of microstructure models.JournalofFinancialandQuantitativeAnalysis,2004,39(2):305-326.
[9]BLEANEY M,LI Z.A new spread estimator.ReviewofQuantitativeFinanceandAccounting,2016,47(1):179-211.
[10] AMIHUD Y,HAMEED A,KANG W,et al.The illiquidity premium:international evidence.JournalofFinancialEconomics,2015,117(2):350-368.
[11] BLEANEY M,LI Z.The performance of bid-ask spread estimators under less than ideal conditions.StudiesinEconomicsandFinance,2015,32(1):98-127.
[12] FONG K,HOLDEN C W,TRZCINKA C A.Whatarethebestliquidityproxiesforglobalresearch?.Sydney,NSW:University of New South Wales,2016.
[13] MARSHALL B R,NGUYEN N H,VISALTANACHOTI N.Transaction costs in an illiquid order-driven market.Accounting&Finance,2016,56(4):917-933.
[14] GOYENKO R Y,HOLDEN C W,TRZCINKA C A.Do liquidity measures measure liquidity?.JournalofFinancialEconomics,2009,92(2):153-181.
[15] HOLDEN C W,JACOBSEN S.Liquidity measurement problems in fast,competitive markets:expensive and cheap solutions.TheJournalofFinance,2014,69(4):1747-1785.
[16] CHORDIA T,ROLL R,SUBRAHMANYAM A.Recent trends in trading activity and market quality.JournalofFinancialEconomics,2011,101(2):243-263.
[17] ANGEL J J,HARRIS L,SPATT C S.Equity trading in the 21st century.QuarterlyJournalofFinance,2011,1(1):1-53.
[18] KIM S,MURPHY D,JAGANNATHAN R,et al.Theimpactofhigh-frequencytradingonstockmarketliquiditymeasures.Atlanta,GA:Georgia Institute of Technology,2013.
[19] EASLEY D,DE PRADO M M L,O′HARA M.Flow toxicity and liquidity in a high-frequency world.TheReviewofFinancialStudies,2012,25(5):1457-1493.
[20] DEUSKAR P,JOHNSON T C.Market liquidity and flow-driven risk.TheReviewofFinancialStudies,2011,24(3):721-753.
[21] BEN-REPHAEL A,KADAN O,WOHL A.The diminishing liquidity premium.JournalofFinancialandQuantitativeAnalysis,2015,50(1/2):197-229.
[22] BOULATOV A,GEORGE T J.Hidden and displayed liquidity in securities markets with informed liquidity providers.TheReviewofFinancialStudies,2013,26(8):2096-2137.
[23] 卢斌,华仁海.基于MCMC方法的中国期货市场流动性研究.管理科学学报,2010,13(9):98-106,128.
LU Bin,HUA Renhai.Research on liquidity of Chinese futures markets via MCMC method.JournalofManagementSciencesinChina,2010,13(9):98-106,128.(in Chinese)
[24] 沈虹.基于综合流动性度量指标的中国期货市场流动性溢价研究.数理统计与管理,2013,32(2):315-322.
SHEN Hong.Research on liquidity premiums in Chinese futures market based on integrated liquidity measuring index.JournalofAppliedStatisticsandManagement,2013,32(2):315-322.(in Chinese)
[25] 李泽海,刘海龙.期货合约流动性度量方法及实证分析.系统管理学报,2012,21(1):29-33.
LI Zehai,LIU Hailong.A liquidity model of futures contracts and its empirical analysis.JournalofSystemsandManagement,2012,21(1):29-33.(in Chinese)
[26] 刘向丽,汪寿阳.中国期货市场日内流动性及影响因素分析.系统工程理论与实践,2013,33(6):1395-1401.
LIU Xiangli,WANG Shouyang.The intraday trend and impact factor analysis on liquidity of Chinese futures market.SystemsEngineering-Theory&Practice,2013,33(6):1395-1401.(in Chinese)
[27] 史永东,王谨乐.中国期货市场各板块间风险传导效应研究.经济学动态,2014(11):70-77.
SHI Yongdong,WANG Jinle.China′s futures market risk conduction effect between each plate.EconomicPerspectives,2014(11):70-77.(in Chinese)
[28] 王硕,李鹏程,杨宝臣.基于指令驱动市场EKOP模型的异质期望研究.管理科学,2016,29(3):123-135.
WANG Shou,LI Pengcheng,YANG Baochen.Heterogeneous expectations study based on EKOP model under order driven market.JournalofManagementScience,2016,29(3):123-135.(in Chinese)
[29] HARRIS L.Statistical properties of the roll serial covariance bid/ask spread estimator.TheJournalofFinance,1990,45(2):579-590.
[30] LEE C M C,READY M J.Inferring trade direction from intraday data.TheJournalofFinance,1991,46(2):733-746.
[31] ODDERS-WHITE E R.On the occurrence and consequences of inaccurate trade classification.JournalofFinancialMarkets,2000,3(3):259-286.
[32] AMIHUD Y.Illiquidity and stock returns:cross-section and time-series effects.JournalofFinancialMarkets,2002,5(1):31-56.
[33] HARRIS L.Estimation of stock price variances and serial covariances from discrete observations.JournalofFinancialandQuantitativeAnalysis,1990,25(3):291-306.
[34] HASBROUCK J.The dynamics of discrete bid and ask quotes.TheJournalofFinance,1999,54(6):2109-2142.
[35] HARRIS L.Minimum price variations,discrete bid-ask spreads,and quotation sizes.TheReviewofFinancialStudies,1994,7(1):149-178.
[36] HARRIS L.Stock price clustering and discreteness.TheReviewofFinancialStudies,1991,4(3):389-415.
[37] KANDEL E,MARX L M.Nasdaq market structure and spread patterns.JournalofFinancialEconomics,1997,45(1):61-89.
[38] DUTTA P K,MADHAVAN A.Competition and collusion in dealer markets.TheJournalofFinance,1997,52(1):245-276.
[39] HASBROUCK J.Security bid/ask dynamics with discreteness and clustering:simple strategies for modeling and estimation.JournalofFinancialMarkets,1999,2(1):1-28.
FundedProject:Supported by the National Natural Science Foundation of China(71271223) and the Program for New Century Excellent Talents in University(NECT-13-1054)
Biography:LIU Zhidong, doctor in management, is a professor in the School of Management Science and Engineering at Central University of Finance and Economics. His research interests include financial engineering and financial econometrics. His representative paper titled “The non ornstein-uhlenbeck models driven by the general lévy process and its bayesian inference” was published in theChineseJournalofManagementScience(Issue 8, 2015). E-mail:liu_phd@163.com
JIANG Ling is a master degree candidate in the School of Management Science and Engineering at Central University of Finance and Economics. Her research interest focuses on financial engineering. E-mail:freeling610@126.com
□
TradingCosts,LiquidityandAssetPricingforFuturesMarketswithBayesianParameterEstimation
LIU Zhidong,JIANG Ling
School of Management Science and Engineering, Central University of Finance and Economics,Beijing 100081, China
A liquid future market serves not only to reduce the transaction cost and discover price, but also helps design investment strategies and lower risk for investors. But the effective transaction cost is usually hard to measure due to the incompleteness of data and we need to estimate the effective transaction cost. Liquidity is the key indicator of future market′s efficiency and the key challenge is to identify good measures of liquidity. A growing literature has focused on the effect of liquidity (and transaction cost) on expected stock return in both academia and financial industry but there is no systematic research on the liquidity effects in the future market. Therefore we need to propose a model to liquidity from the perspective of market micro-structure and asset pricing perspective and to study if liquidity is priced cross-sectionally in the future market. High frequency data contains large amount of information and we need to focus on the research questions, such as the characteristic and measure of liquidity and effect of liquidity and transaction cost in the future market.
Therefore we propose a sequential trading model by using the Bayesian method to compare different measures of liquidity and choose the best measure of transaction cost. Then the measures are corrected for information asymmetry and micro-structure noise. Combined with realized return with transaction costs, we come up with an asset pricing model which also accounts for the economics of scale and cyclical effect in the future market. The data comes from Chinese Future Market.
We show that liquidity measure based on Bayesian estimation using high-frequency data have large advantages over the traditional method of moments. The empirical results are as follows: Order has a significant price impact and it means private information is incorporated in the order. Liquidity measures based on complete model and transaction data are better since they have a higher correlation compared with the estimation of defined method. Transaction cost is included in the excess return. Transaction cost has a cyclical effect on asset prices. Therefore liquidity has a large impact on the return of futures.
We propose a sequential trading model, using Bayesian estimation with high frequency data to study the liquidity effect in the future market. The paper will draw a much clearer picture of liquidity, transaction cost and return for the participants in the future market. Also it will shed light on the regulatory policy to increase market quality, liquidity and efficiency and to reduce the transaction cost in the future market.
trading cost;liquidity;asset pricing;Bayesian parameter estimation;high frequency transaction data
Date:August 19th, 2016AcceptedDateDecember 31st, 2016
F830.9
A
10.3969/j.issn.1672-0334.2017.01.013
1672-0334(2017)01-0146-14
2016-08-19修返日期2016-12-31
国家自然科学基金(71271223);教育部新世纪人才支持计划(NECT-13-1054)
刘志东,管理学博士,中央财经大学管理科学与工程学院教授,研究方向为金融工程和金融计量等,代表性学术成果为“Lévy过程驱动的非高斯OU随机波动模型及其贝叶斯参数统计推断方法研究”,发表在2015年第8期《中国管理科学》,E-mail:liu_phd@163.com 姜玲,中央财经大学管理科学与工程学院硕士研究生,研究方向为金融工程等,E-mail:freeling610@126.com
