闭环控制回路多指标性能评价

赵洪洲 赵 众 朱 磊

(北京化工大学信息科学与技术学院)

闭环控制回路多指标性能评价

赵洪洲 赵 众 朱 磊

(北京化工大学信息科学与技术学院)

针对目前基础回路控制器性能评价方法存在直观性差、易读性差和不可溯源的问题，提出一种多指标性能评价方法。采用相对性能指数评价回路的响应和设定值跟踪情况，采用振荡指数指标评价回路振荡情况，采用有效投用率评价控制器的投用情况。仿真与工业应用结果均证实了所提方法的可行性和有效性。

基础回路控制器 闭环控制回路 多指标性能评价 有效投用率

基础回路的自动控制投用率和自动控制效果是提高产能、减少人工劳动力的根本所在[1]。目前，提高回路自动控制投用率和效果的常用方法有最小方差控制基准评价方法、应用于多变量系统的最小相位评价方法[2]及线性二次高斯控制基准评价方法[3]等。其中，最小方差控制基准评价方法已从单回路拓展到了多入多出系统、非最小相位系统及先进控制系统等。

然而，在实际工业过程中现有的方法仅能给出控制器的评价结果，导致现场操作人员理解难度大、学习成本高。为此，笔者提出了一种闭环控制回路多指标性能评价方法，根据采集到的闭环控制回路生产数据，计算控制回路的多项指标，推断控制器性能下降的可能原因，以便进行辅助维护。

1 系统模型

闭环控制回路系统框图如图1所示。

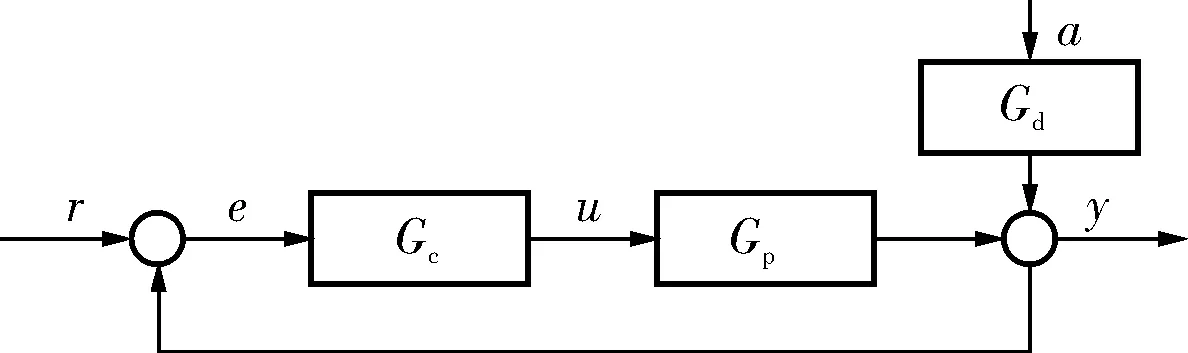
图1 闭环控制回路系统框图

则脉冲响应模型为：

y(k)=Gd(q-1)a(k)+Gp(q-1)Gc(q-1)(r(k)-y(k))

(1)

式中r(k)-y(k)——拉氏变换运算符；

q-1——偏差。

模型辨识方法选择子空间辨识方法[4,5]，其表达式如下：

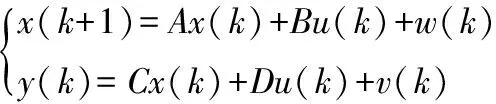
(2)

式中A、B、C、D——系统模型矩阵；

u(k)——控制器输出,u(k)∈Rm；

v(k)——系统过程中的测量噪声干扰,v(k)∈Rl；

w(k)——系统过程中的噪声干扰,w(k)∈Rn；

x(k)——过程状态量,x(k)∈Rn；

y(k)——系统输出,y(k)∈Rl。

设k为某一时间点，f为预计的周期，则式(1)可转换为：

yf=Γfx(k)+Hfuf+Gfwf+vf

(3)

其中，向量yf、uf、wf、vf、Γf为广义可观测矩阵。

子空间通常由两步计算得到模型：

b. 得出系统模型矩阵。

系统的模型阶次与f成正相关关系，如果选择的f过大，则系统阶次过高，导致计算量增加。为此可以采用奇异值分解得到系统阶次的最佳值。基于正交投影原理，根据QR分解和SVD分解，得到的计算式为：

(4)

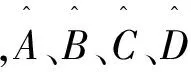
根据Frobenius范数，即可得到A、B、C、D的估计值。转换为传递函数,有：

G(s)=C(sI-A)-1B+D

(5)

2 多指标性能评价

2.1相对性能指数

相对性能指数(Relative Performance Index,RPI)用以显示控制相对于基准值的响应速度，其中基准值是根据期望稳态时间得到的。RPI值越接近1就表示系统传递函数的响应效果越接近预期设定值，控制性能越好，小于1则为较差，大于1则表示系统响应速度快于预期设定值。RPI的计算式为：

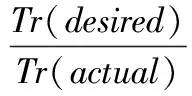
式中Tr(actual)——实际辨识模型的稳态时间；

Tr(desired)——基准模型的稳态时间。

闭环回路中，将控制器和过程对象闭环后，可近似作为一个二阶系统进行分析。在二阶系统中：

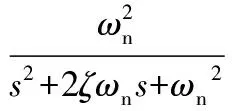
(6)

当系统无阻尼振荡频率ωn不变时，阻尼比ζ越大，系统超调量越小，系统稳定性越强；但同时系统响应会变慢，稳态时间会变长。根据实际操作经验，ζ的理想取值为0.6～1.0。

系统响应时间ts的计算式为：

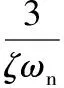
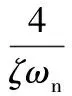
(7)

其中，V为相对误差。根据式(7)可以反推出ωn，然后即可得到式(6)的数学表达式。

2.2振荡指数

振荡是受控变量变动中具有重复性的现象。受控变量处于振荡状态时，除影响自身的稳定性外，还会影响前后回路的稳定性[6]。采用自相关系数计算振荡指数ρk，则有：

(8)

式中k——滞后数；

yt——t时刻的测量值；

自相关函数对于变量在不同时间的值的相关程度有较好的度量。振荡指数越大，越接近1，说明振荡越强；反之越平稳。

2.3有效投用率

投用率是生产平稳的重要表征指标，通常越高越好。但是该投用率只是DCS端控制回路状态量的值，对于控制器是否真实有效，阀门是否起作用无从得知。因此笔者提出有效投用率指标，用以评价控制器的实际效果。有效投用率是以控制器真正起作用时间的占比进行计算的。将控制器无效的时间段和操作量MV值饱和状态时间段去除，从而得出控制器的有效时间。其计算公式如下：

(9)

投用率和有效投用率的数据曲线如图2所示，可以看出，虽然DCS端控制回路全程显示投用，但是控制器控制效果有限，其有效投用率仅为53.58%。

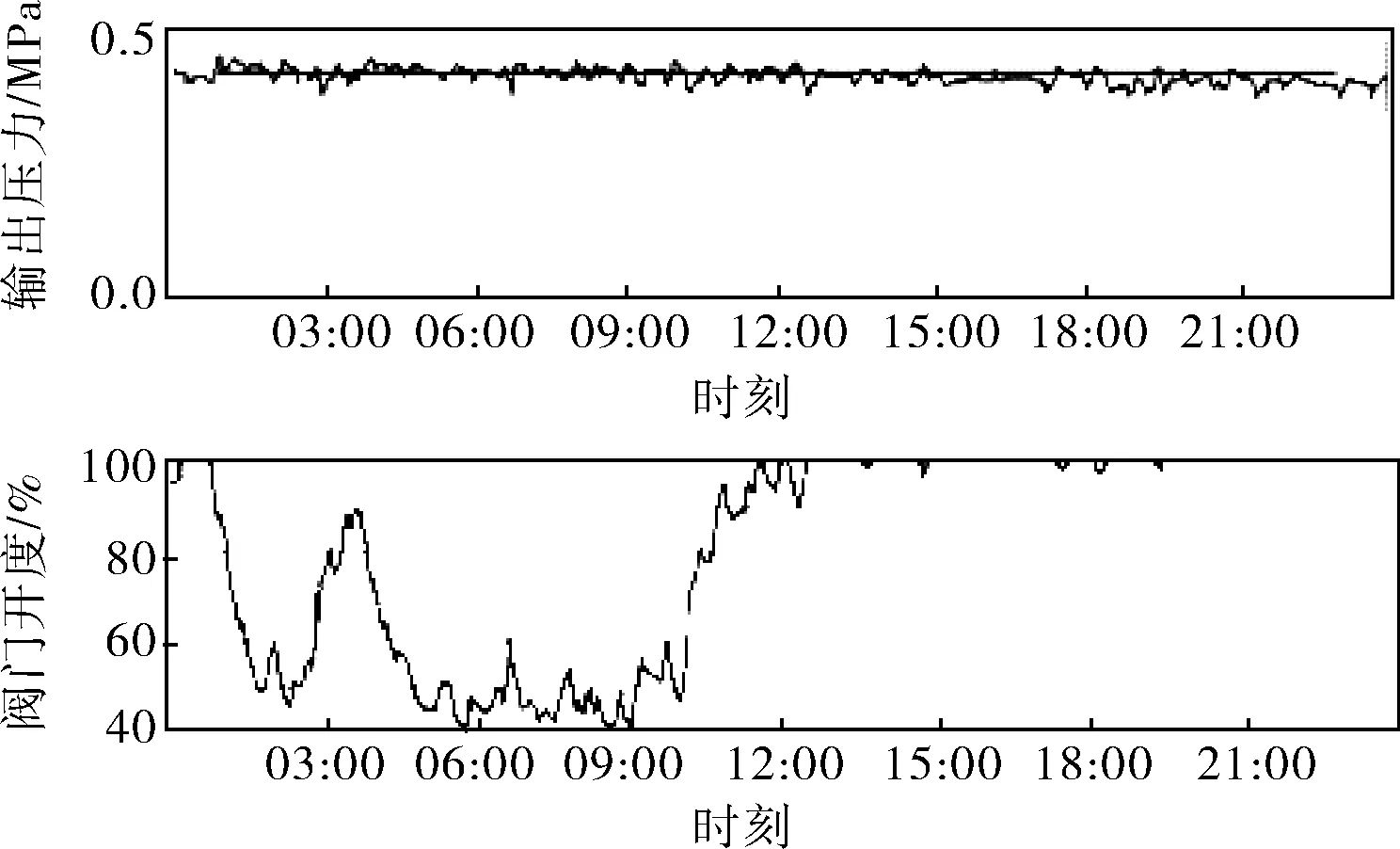
图2 投用率和有效投用率的数据曲线

3 应用情况

基于闭环控制回路多指标性能评价方法，笔者开发了相应的控制器性能评价(Controller Performance Analysis,CPA)软件。在某化工企业的现场应用系统结构框图如图3所示。CPA软件通过OPC工业标准采集生产过程中的数据，对4个分厂的6 000多个基础控制回路进行实时监控。CPA软件对所监控的基础控制回路给出优、良、中、差4个等级，并提供控制性能的改进建议。

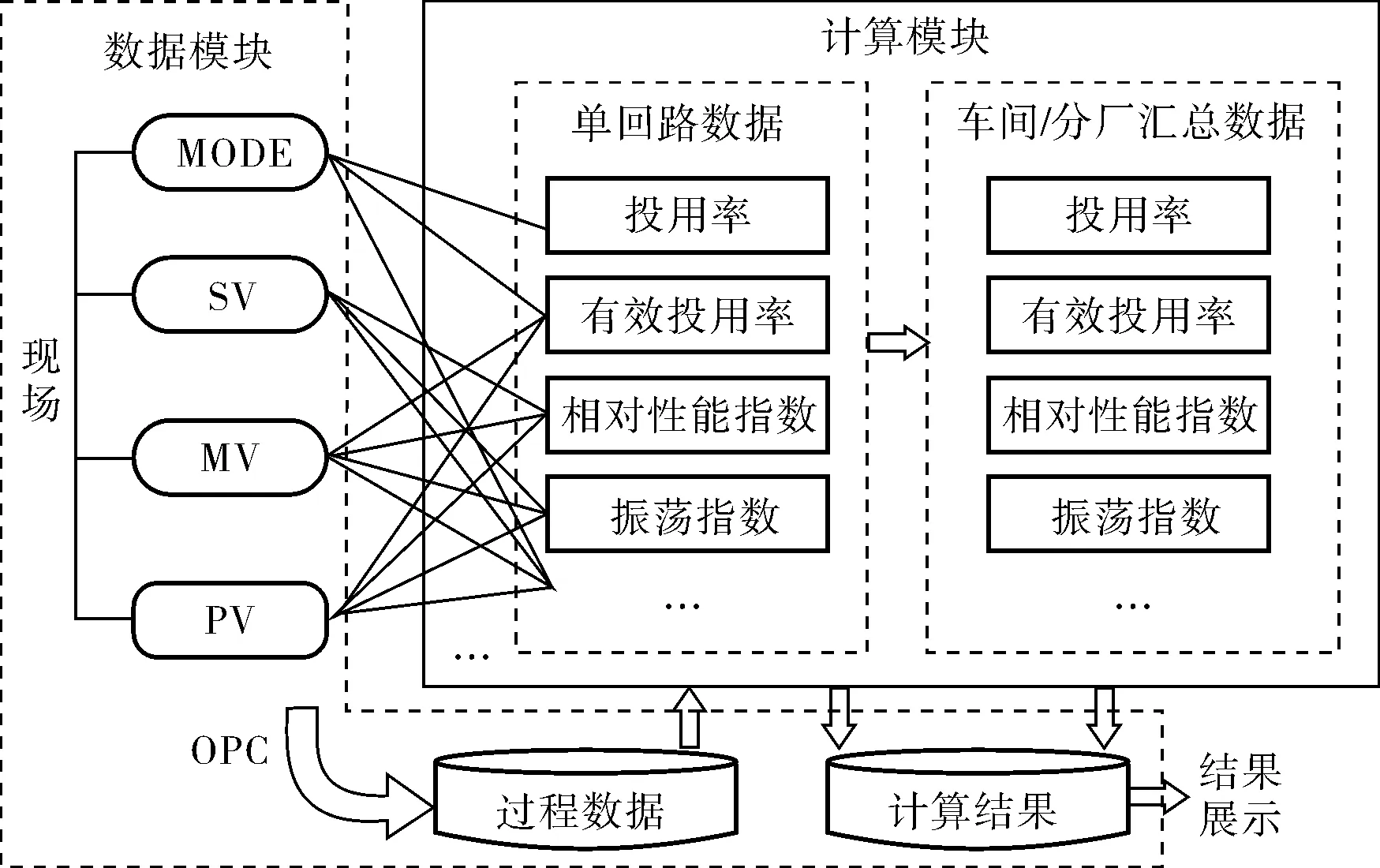
图3 某企业现场应用系统结构框图

图4为评价结果为中的回路详细报告。其中，期望稳态时间为600s，未达到预设要求。实测值PV跟随设定值SV良好，且PV与控制器输出MV相匹配，说明MV的作用效果明显，因此有效投用率较高。但是回路曲线整体存在明显的振荡，所以综合后的评价结果为中。

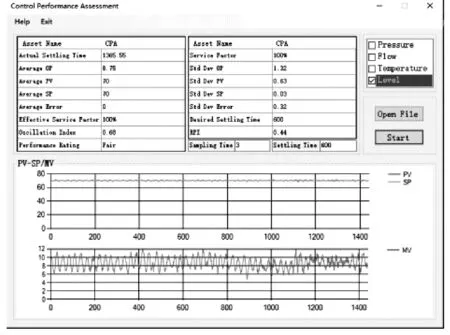
图4 评价结果为中的回路详细报告

图5为评价结果为差的回路详细报告。其中，期望稳态时间为600s，未达到预设要求。PV跟随SV良好，且PV与MV相匹配。然而MV存在极值状态，此时控制器为放任状态，即认为无效，同时曲线又存在振荡，所以综合后的评价结果为差。

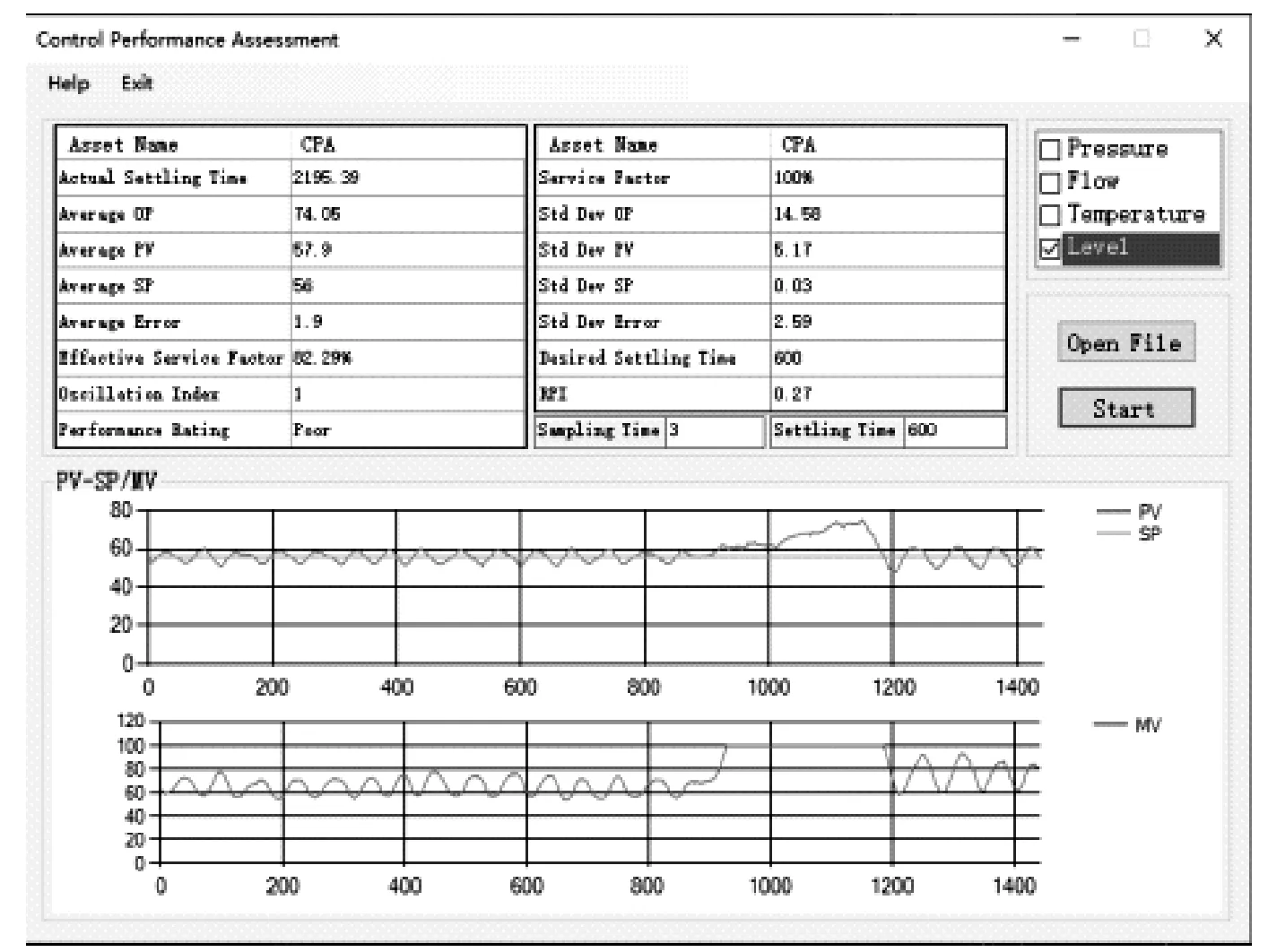
图5 评价结果为差的回路详细报告

4 结束语

针对目前控制器性能评价方法存在直观性差、易读性差和不可溯源的问题，提出了一种多指标控制器性能评价方法。仅通过生产过程中的实际数据，即可评价回路的控制性能，并可根据不同指标的不同评价结果，有针对性地查找问题出处。各项指标与生产过程紧密结合，提高了控制器性能评价的可用性。仿真结果和工业应用结果均证实了笔者所提方法的可行性和有效性。

[1] Mcmillan G K.Tuning and Control Loop Performance[M].New York:Momentum Press,2014.

[2] Thornhill N F,Huang B,Zhang H.Detection of Multiple Oscillations in Control Loops[J].Journal of Process Control, 2003,13(1):91～100.

[3] Huang B.Performance Assessment of Processes with Abrupt Changes of Disturbances[J].Canadian Journal of Chemical Engineering,2010,77(5):1044～1054.

[4] 罗小锁.基于子空间辨识的预测控制方法研究[D].重庆:重庆大学,2011.

[5] 罗小锁,陈学昌,曹保山.有色噪声条件下的子空间辨识改进方法及应用[J].计算机工程与应用,2015,51(1):234～237.

[6] Liao K,Xu Y,He Z,et al.Second-order Sliding Mode Based P-Q Coordinated Modulation of DFIGs against Interarea Oscillations[J].IEEE Transactions on Power Systems,2017,PP(99):1.

EvaluationofControlLoopPerformancewithMultiple
IndexBasedonSubspaceModelIdentification

ZHAO Hong-zhou, ZHAO Zhong, ZHU Lei

(CollegeofInformationScienceandTechnology,BeijingUniversityofChemicalTechnology)

Considering poor intuition and readability and traceability of existing basic loop controller’s performance evaluation method, a multi-index-based comprehensive evaluation method was proposed. Having relative performance index adopted to evaluate both loop response and the set point’s tracking ability was implemented, including having oscillatory index employed to evaluate closed loop’s oscillation feature and the effective service index taken to evaluate the controller’s application effect. The simulation and industrial application results verify both feasibility and effectiveness of this method proposed.

basic loop controller, closed control loop, multi-index performance evaluation, application effect

北京市自然科学基金项目(4172044)。

赵洪洲(1988-)，硕士研究生，从事生产过程系统模型辨识与性能评测的研究。

联系人赵众(1970-)，教授，从事先进控制、过程监测、工业控制系统集成的研究，zhaozhong@mail.buct.edu.cn。

TH865

A

1000-3932(2017)11-1019-04

2017-05-23，

2017-08-14)

2018慕尼黑上海电子生产设备展

展会时间2018年3月14～16日展会地点上海新国际博览中心

2018慕尼黑上海电子生产设备展将于2018年3月14～16日在上海新国际博览中心举办。本届展会汇聚国内外领先设备厂商，展品范围涵盖整个电子行业产业链，包括SMT表面贴装技术、线束加工和连接器制造、电子制造自动化、运动控制、点胶注胶、焊接、电子和化工材料、EMS电子制造服务、测试测量、PCB制造、电磁兼容、元器件制造(绕线机、冲压、灌装、涂敷、分选、打标等)和组装工具等。联合同期举办的慕尼黑上海电子展(Electronica China)，展会规模将突破80 000平方米，预计参展商数量将超过1 400家，海内外观众数量将达到70 000名。琳琅满目的创新设备和制造科技，工业4.0和智慧工厂理念与实践相结合，Productronica China “智”在创新，带您尽览未来电子科技！

主办方慕尼黑展览(上海)有限公司

地址上海市浦东新区源深路1088号平安财富大厦11楼

邮编200122

电话+86-21-2020 5516传真+86-21-2020 5688/5699

邮箱jenny.liu@mm-sh.com