让数学课堂彰显思维的活力

沈亚++倪燕

[摘 要]

通过对“三角形的认识”课例片断的回放与剖析，追根究源。在此基础上，反思与重构教师的教学内容和行为，把学生知识的自我建构作为核心要素，“以学生为中心”，进而探寻提升数学课堂思维活力的具体方法。

[关键词]

数学思维；三角形；作高

活力，指旺盛的生命力，行动上、思想上或表达上的生动性。而数学课堂中的活力，主要指学生数学思维或数学表达的生动性。学生是具有生命力的个体，教师亦然，数学课堂成为师生、生生思维碰撞的主阵地。“数学是思维的体操”，而数学教学是数学思维活动的教学。下面，笔者现结合苏教版四上“三角形的认识”一课，阐述如何让数学课堂彰显思维的活力。

一、现象与剖析

回放片断1：

（1）三角形是一种在我们生活中应用很广泛的图形，请你指一指。

（2）找三角形：你能从图中找出三角形吗？

（3）说说生活中还有哪些地方能看到三角形？

（4）揭示课题，今天我们来学习：三角形的认识

通过回放，不难发现：学生在二年级的时候，明明已经初步认识了三角形，可还是要按照指示重新认识三角形，孩子心中不免疑窦丛生：这三角形我早就认识了，一点儿也不好玩。是呀，人对于已经了解熟悉的事物，他们是毫无兴趣可言的，無非是在不同的情景图中寻找熟悉的三角形。教师如此一厢情愿地授课，致学情于不顾，学生很难有主动思考的积极愿望，思维总是旋转在一个较低的水平。这样的教学就像空中楼阁，它不仅脱离了教学的实际需要，也不能满足学生的心理需求，在课的开始，错失了启迪思维的最佳时机。

回放片断2：

（1）画一个三角形，说说三角形有什么特点？

（2）自学书上第75页三角形各部分名称，并在自己画出的三角形上标出各部分名称，指着图说说三角形有几条边、几个角和几个顶点。

（3）小组交流，汇报展示。

（4）“练一练”第一题。交流判断的理由。

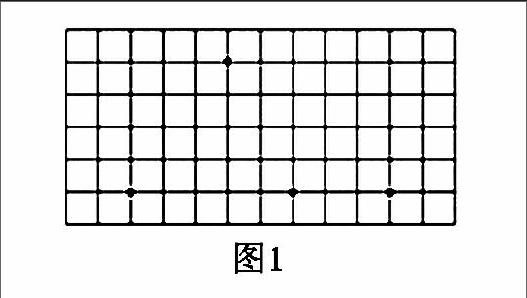
（5）“试一试”。讨论：以同一条直线上的这3个点作为顶点，为什么不能画出一个三角形呢？（如图1）

<＼＼Pc-006＼tm＼中小学＼2017＼11期＼t11q-47.tif>

学生自己画的一个三角形，找的特点仅仅针对个体而言，显然不具有普遍性，因而会出现：三角形是斜的，三角形有的大有的小等这类非本质属性。小学生的知觉比较粗糙，顿悟能力不强，很容易受到三角形外观因素的影响。自学内容看似发挥学生的主观能动性，实际情况是学生一旦看着三角形的标准概念，自然会不假思索地照本宣读，如此心照不宣的“默契”配合，轻而易举地处理本课的教学重点，这样急功近利的教学行为，学生的思维毫无可以生长的土壤。更令人隐忧的是：从长远来看，学生对这种“明知故学”的学习模式将逐渐失去探究的兴趣，数学思维更是止步不前。

回放片断3：

（1）自主阅读书本第76页上的内容。

①说一说：什么是三角形的高和底？

②画一画：完成“试一试”

③猜一猜：每个三角形有几条高？

（2）结合操作过程交流。

（3）完成第76页练一练2

（4）练习十二第一题。学生独立完成，再交流画三角形高的方法。

重点讨论直角三角形的高

（5）练习十二第二题。

①按要求画三角形。

②检查画出的三角形的底与高是否符合要求

③交流画法

学生的学习过程不可替代，学生的理解也催熟不得。本课的难点是如何作三角形底边上的高，如果学生完全遵照教师的引导来学习，那么学生本身有多少求知欲？对于不同形状的三角形的三条高这个难点没有突破，学生学得云里雾里，心中纳闷：为什么不同的三角形却都有三条高？即使有图有真相，但走马观花似的欣赏，阅过即忘。

教师按照教材，照本宣科，学生按照教师指示，按部就班，这样的教学能否点燃学生的学习热情？能否将学生的数学思维被激活？为知识而教，为教材而教，为任务而教……这原本就有违我们教育教学的初衷。促进学生的全面发展才是教学之根本，“无论何种教育，归根结底只有通过学生自身的选择与建构，才有可能真正形成学生发展的现实。”教师应当站在儿童的视角出发，重新审视自己的教学，只有在学有所困、学有所惑、学有所难的地方做推敲与深究，才有可能让学生的思维绽放出思维的活力。下面仍以“三角形的认识”为案例，笔者从以下三个方面进行调整。

二、重构与反思

1.有贴切的情境才有活力的需求

重构：情境导入，产生认知需求。

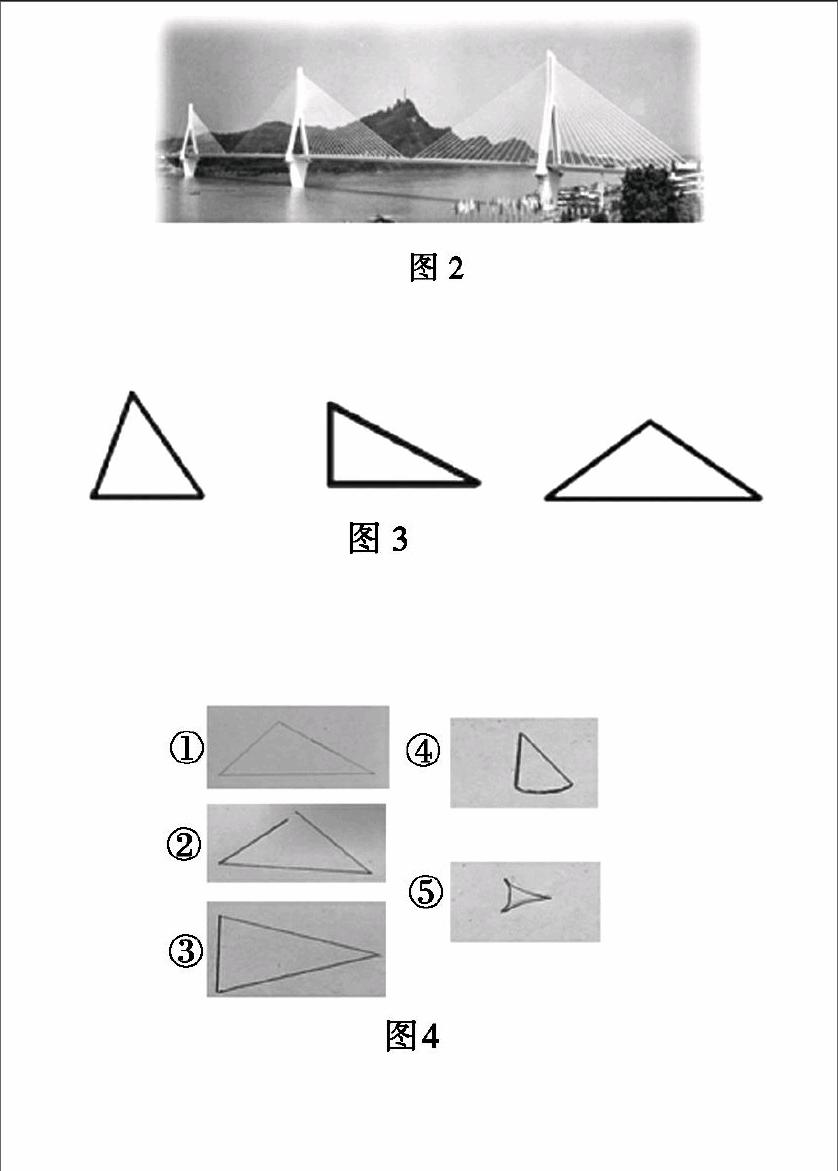
（1）同学们这是一座雄伟的斜拉桥，你能在图中找到三角形吗？（如图2）用手比画比画。

<＼＼Pc-006＼tm＼中小学＼2017＼11期＼t11q-48.tif>

（2）生活中还有哪些地方能见到三角形？（如图3）

<＼＼Pc-006＼tm＼中小学＼2017＼11期＼t11q-49.tif>

（3）今天咱们进一步认识三角形。

反思：斜拉桥是教材给出的情境图，也是学生耳熟能详的桥梁样式，直接要求学生在图中手势比画出三角形，参与的面广，出现的三角形样式多。它们形状各异、大小不同，从生活中情景图中的三角形脱离出数学上的三角形，简洁、清晰、明了。启发学生迫切学习的愿望，“进一步认识三角形”一下子揭示了课题，有助于学生快速进入学习的启程状态，也为后面的教学难点作三角形的高留足时间。

2.有多元的感知才有活力的表象

重构：三角形的概念

（1）请你任意画两个三角形，想想三角形有什么特点？

（2）这是部分同学画的三角形，你有什么想说的吗？（如图4）endprint

（3）为什么②号、④号和⑤号不是三角形？（相机板书：首尾相接、三条线段）

（4）为什么①号和③号是三角形？要讲道理的哟！

出示：三条线段首尾相接围成的图形叫做三角形。

（5）我们的三角形与点有着密切的联系。瞧，淘气的小圆点也来凑热闹了。给你三个点能画一个三角形吗？（如图组5①）

（6）其中的一个小圆点跑到了这儿，谁來围一围。（如图组5②）

（7）看看淘气的小点点又蹦到了哪里？一起比画比画。（如图组5③）

（8）这回淘气的小圆点又蹦到了这里，你能再连成一个三角形吗？（不能）为什么？（如图组5④）

反思：小学生的思维是形象直观的，如果能提供清晰而具体的感知材料，他们感知到一定数量，在一定程度上，抽象思维的萌芽会悄悄地开始。判断是否是三角形，一眼便知，而三角形的概念较为抽象，如何让抽象的概念形象直观化，通过“错例”与“正例”一目了然的比较，则形象直观地阐述了“首尾相连”、“三条线段”、“围成”等抽象的数学概念，便于学生理解，学生的作业与授课内容的紧密结合，能将学生的思维火花彻底点燃。思维是从惊奇和疑惑开始的，学生有了问题才会产生自主探究的欲望，将“试一试”的原题进行变式，4个小圆点分别出示，惯性思维下学生陷入“只要有3个点就能围成一个三角形”的误区，而最后出示“以同一条直线上的这3个点作为顶点”这样的图示，学生惊讶地发现：围成三角形的3个顶点不能在同一条直线上。一下子将学生的思维方向发生了惊天大逆转，这样的教学有效地克服学生的思维定式。数学学科的魅力恰恰就在于它的思维之美。

3.有层次的建构才有活力的思考

重构：作高，突破各种三角形。

1.认识三角形的高和底

（1）这辆卡车拖着人字梁在高架桥下面走，高架桥限高3米，这卡车能顺利通过高架桥吗？谁知道限高3米是什么意思？（如图6）

（2）要判断卡车能不能顺利通过高架桥，你觉得要量出哪条线段的高度，谁来指一指。

（3）这条线段和人字梁的底边有什么关系？

（4）是否垂直呢？咱们请出三角尺帮忙验证一下。

（5）同学们知道吗，像这样从三角形人字梁的一个顶点到它对边画一条垂直线段，这条垂直线段的长度就是这个三角形人字梁的高，这条对边是三角形人字梁的底。

2.锐角三角形中的高

（1）刚才我们认识了三角形人字梁中的底和高，如果是一个普通的三角形，你还能找到底和高吗？如果以这条边为底，这条底边上的高在哪里呢？赶紧动笔在练习纸上找一找，画一画。

（2）画三角形的高咱们可以分成这样三步：（如图7）

①找：找出底所对的顶点；

②合：一条直角边→底边，另一条直角边→底边；

③画：画出顶点到对边的垂直线段，标高、直角标记。

（3）这画高的方法和以前学的哪个知识有相似的方法？

（4）谁愿意到黑板上分三步画一画三角形底边上的高？

（5）如果我们把三角形旋转（如图8），你有什么发现？

（6）如果以另一条边为底，你能画出这条底边上的高吗？我们就用这样的三步画出这条底边上的高，在练习纸上画一画吧。

（7）三角形还有这第三条边呢，如果以这条边为底，你能想象一下它的高是怎样的吗？来，想一想，举起手来比画比画。

3.直角三角形中的高

（1）瞧，我们的直角三角形也来凑热闹了，它有两条直角边和一条斜边围成。如果以这条直角边为底，你能画出这条底边上的高吗？动笔在练习纸上画一画。

（2）你们有什么惊奇的发现？

（3）那我们想象一下，如果以这条直角边为底边，它对应的高在哪里呢？（如图9）

（4）直角三角形以斜边为底，它的高又在哪里呢？

同桌互相用三角尺检查一下！（如图9）

（5）直角三角形里也有几组对应的底和高？

4.钝角三角形中的高

（1）第三次画三角形，还给你们准备了方格纸，以这条5厘米的线段为底，画高为3厘米的三角形，谁画的多？（如图10）

（2）这个特殊的三角形，它的高有几条呢？感兴趣可以去研究。

（3）演示，看来这些所有的三角形的高其实就是这两条平行线中间的距离都是3厘米。

反思：作高历来是三角形教学中一块最难啃的骨头，为学生学习之难点，教师教学之痛点。根据学生的认知规律和已有经验，以新知识的核心作为切入点，步步为营，层层递进。巧妙地设计卡车运人字梁，遇到限高问题的生活情境。引发学生解决问题的迫切需求，此时三角形的“底”和“高”顺利自然地引出。一般的教学，教师只会停留在作水平底上的高，至于斜边上的高，经常要求学生自主尝试。众所周知，以斜边为底，三角板位置的放置恰好是学生认知的一个盲点，这时采用旋转三角形的位置，学生不难发现：无论怎样旋转三角形，底与高始终互相垂直，三角板的位置摆放也会随之发生变化。而作高从锐角三角形的扶，总结画高三步骤；到直角三角形的帮，认识到两条直角边互为底和高；最后到钝角三角形的放，对作三角形的“外高”不做具体的要求，愿意探究地可以自主地去发现。满足不同层次的学生探究的需要，并且选择自己感兴趣进行主动探究，提供充分、全面的变式，让学生通过垂直的不同外在形式，认识三角形作高的本质属性，对概念的理解更到位，在“知其然所以然”后获得了深刻的理解。

重构之后的处理充分重视学生的原有基础，探究学生的学习兴趣，更好地启发和发展他们的数学思维。让学生亲历数学知识的发现、发生、发展的过程，激发学生的主观能动性，积极思考，大胆质疑，让学生更加深入的思考问题，使学生的数学思维能真正发生。立足学生的立场，让学生真正感受到“高”的来源，体验“高”的形成，学会作底对应的“高”，这无疑让数学课堂彰显思维的活力，是对学生成长的一种启迪和洗礼。

[参 考 文 献]

[1]任慧.反思与重构——《三角形的高》教学探索[J].教育视界，2016（6）.

[2]楼铁飞，边巨星.从学生错误中寻找三角形作高的教学对策[J].教学与管理，2017（4）.

[3]陈爱仙.呵护儿童立场下的真实学习——重构“认识厘米”[J].中小学数学，2016（5）.

（责任编辑：李雪虹）endprint