一种改进的永磁同步电动机参数在线辨识方法

石有计

（铁岭师范高等专科学校，辽宁 铁岭 112000）

一种改进的永磁同步电动机参数在线辨识方法

石有计

（铁岭师范高等专科学校，辽宁 铁岭 112000）

本文提出了一种永磁同步电动机参数在线辨识的新方法。通过对永磁同步电动机在d-q坐标系下，标准最小二乘法形式的参数辨识模型的推导，利用带遗忘因子最小二乘法（FFRLS）对电动机定子电阻值和交直轴电感值进行在线辨识，借助以上辨识结果，采用模型参考自适应方法（MRAS）再辨识出电动机的永磁磁链。同时应用基于Popov超稳定性理论设计的PI自适应律，实现各种工况下电动机的永磁磁链在线辨识。以一台0.75kW永磁同步电动机为例进行了仿真与实验研究，仿真结果显示，该方法具有计算量较小、准确度较高且具有较佳的动态跟踪辨识特性。

永磁同步电动机；在线辨识；最小二乘法；模型参考自适应法

永磁同步电动机（PMSM）具有结构简单、节能高效、高功率密度、控制精准等诸多优点，易于构成性能优良的伺服控制系统。PMSM控制系统性能的优劣与电动机参数的精确度直接相关法各有优劣：FFRLS结果精准、收敛快速，但计算量比较大。MRAS易受外界因素影响，稳定性较差。而在实际的运行中，PMSM系统表现为一个时变的动态系统，其系统参数例如绕组电阻、电感、转子磁链等参数受温度变化、磁饱和及负载扰动的影响而产生变化，使得控制性能受到影响。为保证相关的控制算法有效运行，需要对电动机参数进行实时辨识。传统的参数辨识方法有：模型参考自适应法、加减速法、最小二乘法、扩展卡尔曼滤波法和人工智能算法等[1]。这些辨识方法虽有欠缺，但计算量较小。本文提出将递推最小二乘法和模型参考自适应法相融合，将两者的优势进行互补，用于永磁同步电动机参数在线辨识。在保证辨识稳态后几乎不影响MRAS辨识精度的前提下，提高MRAS的辨识速度，改善初始辨识过程中的振荡。

1 改进的永磁同步电动机参数在线辨识方法

1.1 带遗忘因子的递推最小二乘法原理

该文中选定性能指标为

式中，μ 为遗忘因子，0＜μ＜1。对于上式的目标函数，其递推公式如下：

式中，θ 为待辨识参数；K为增益矩阵；ϕ 为观测矩阵；P为协方差矩阵。

1.2 定子电阻和交直轴电感辨识

永磁同步电动机在d-q坐标轴系下的状态方程为

式中，ud、uq分别为d轴、q轴电压，id、iq分别为d轴、q轴电流，ω 为 PMSM 转子电角速度，Ld、Lq为d轴、q轴电感，RS为每相定子绕组的电阻，ψf为永磁磁链。

对式（3）进行离散化处理，变形为最小二乘法形式如下：

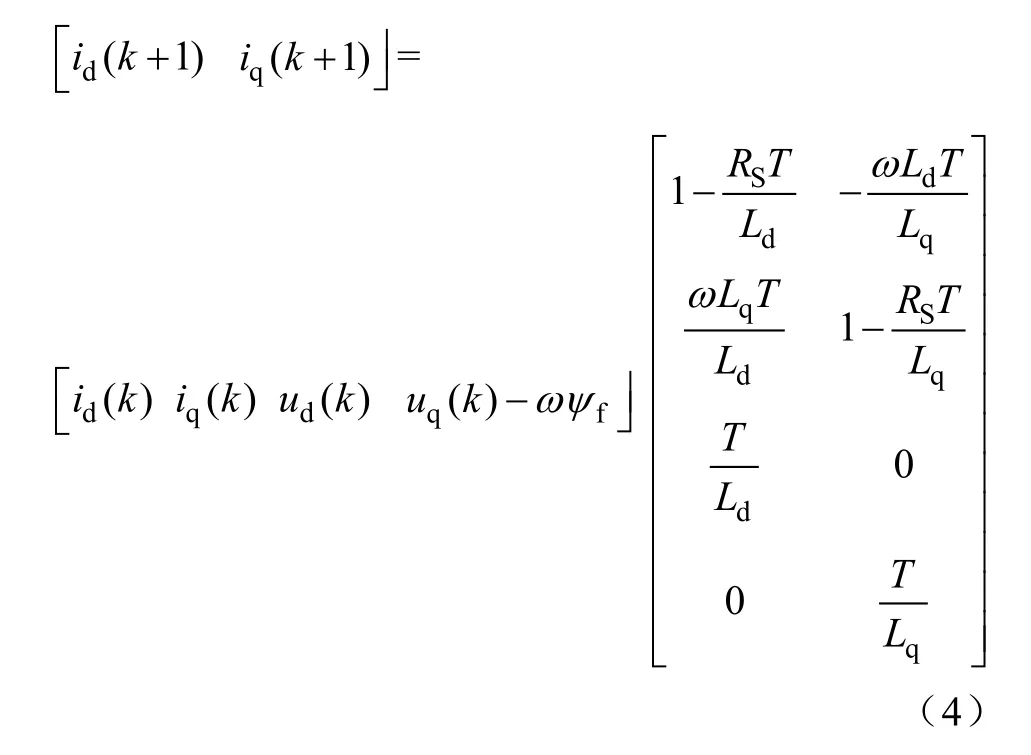
由式（4）可知，式中有未知参数永磁磁链ψf，且ψf只在iq中存在，由此文中采用id=0的矢量控制策略，常态下，id变化非常小，故将式（5）简化为

对式（5）中的RS和L可用FFRLS进行在线辨识，令

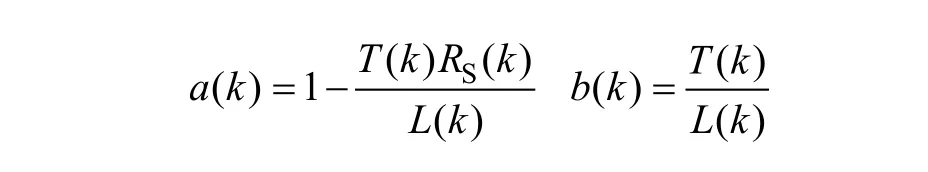
对应的算法模型为

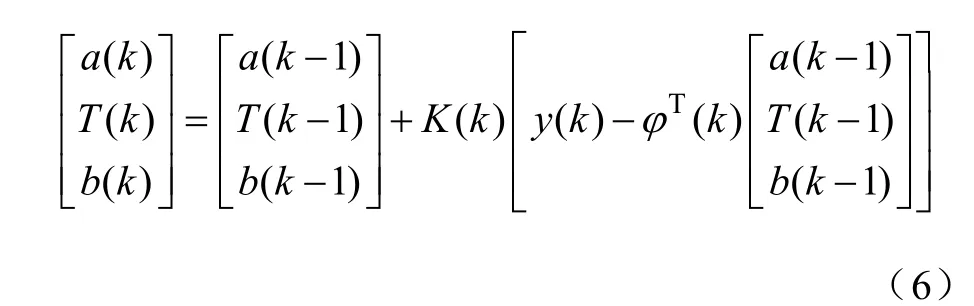
其中：

令 P(0)=αI，α 一般取值为 104～1010。先辨识出a和 b值，再利用a(k)和b(k)关系式求解出定子电阻RS和交直轴电感L。

1.3 永磁同步电动机永磁磁链辨识

对电动机永磁磁链的辨识可利用MRAS方法。MRAS基本结构如图1所示。

图1 模型参考自适应控制结构图

首先将PMSM在d-q坐标系下的参考模型写成如下形式：

由上面推导，将MRAS系统等效成如图2所示构成的系统。

使用Popov超稳定性理论设计自适应规则，要使式（11）所代表的系统稳定，需要满足：①非线性时变部分满足Popov积分不等式；②系统的线性定常前向回路部分严格正实[2]。

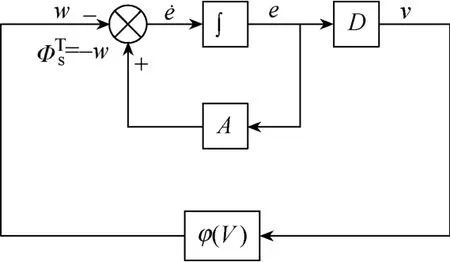
图2 非线性时变系统框图

D是引入的补偿矩阵，为简化计算取补偿矩阵为单位阵，即 D=I，在 MRAS系统中，选用比例+积分结构的自适应律，即

式中，f1(t)、f2(t)为所求参数自适应律中对应的函数，(0) 为是参数n估计的初始值。

根据系统稳定条件1），可得参数ˆn的自适应律为

由以上分析知道，可用图3所示的系统框图对转子磁链进行辨识。

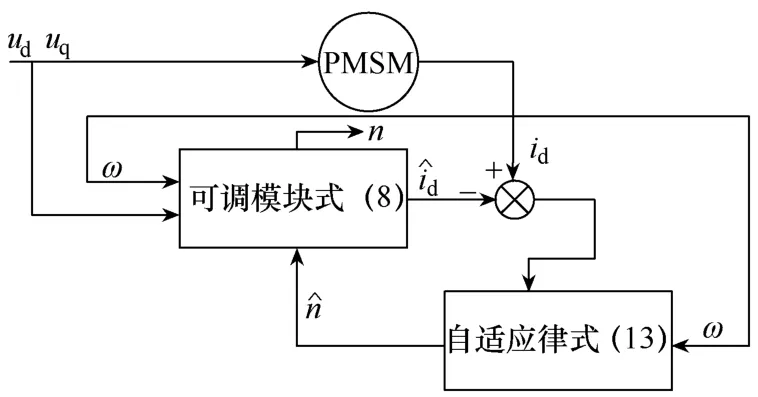
图3 基于MRAS的永磁磁链辨识系统框图

首先利用FFRLS对RS和L进行在线辨识，其后应用MRAS的方法对ψf进行辨识。其辨识方案框图如图4所示。

图4 FFRLS-MRAS电动机参数辨识方法框图

2 电动机参数辨识仿真

2.1 永磁同步电动机参数辨识仿真

利用Matlab的Simulink模块进行仿真验证，搭建 PMSM 双闭环矢量控制系统仿真模型如图 5所示，采用Id=0的控制策略。

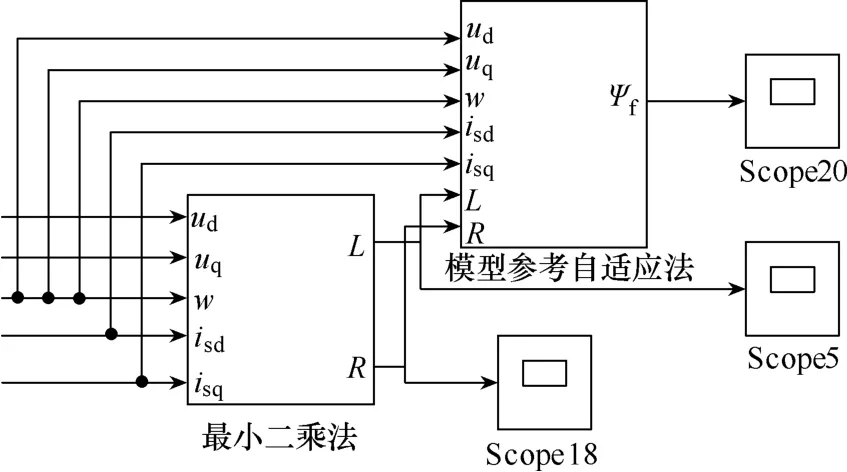
图5 PMSM电气参数在线辨识仿真模型

使用Matlab进行仿真验证。永磁同步电动机参数见表1。

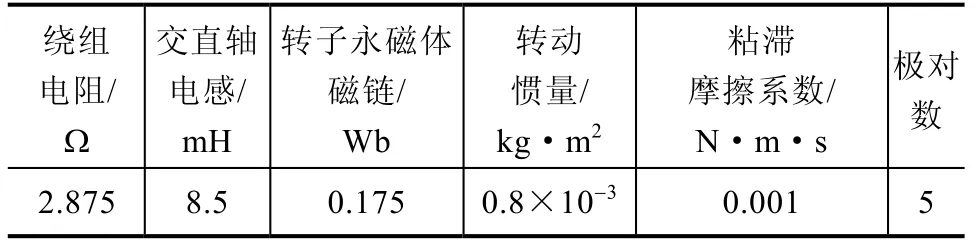
表1 仿真所用电动机参数

2.2 辨识时间间隔和遗忘因子的选择

设置电流采样周期即辨识时间间隔为 0.1ms。参考相关资料知遗忘因子一般选择 0.9以上。下面对电动机参数在不同遗忘因子下进行在线辨识。取各个参数初始值为：RS=2.5Ω，TL=3N·m，转速设定为 30r/min，Lq=Ld=5mH，ψf=0.1Wb，P(0)=105I。图6和图7是仿真结果。

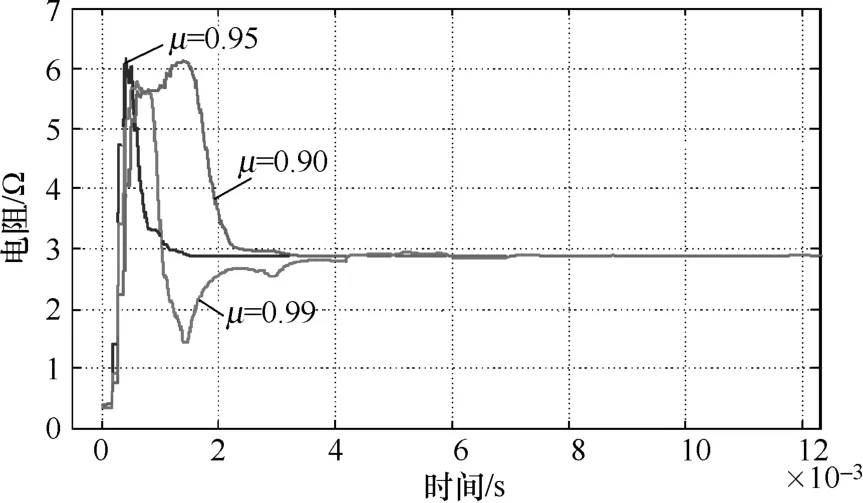
图6 电动机定子电阻在线辨识波形

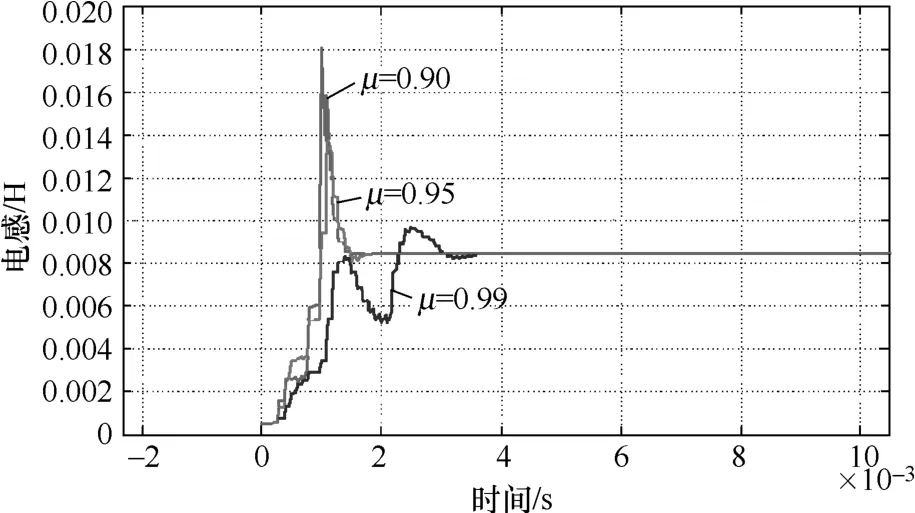
图7 电动机交直轴电感在线辨识波形

分析图 6和图 7的结果可以看出，遗忘因子μ取值不同，其跟随性就不同，μ 越接近1，跟随性越差，辨识值收敛速度越缓慢，但辨识精度越好；μ 越小，跟随性越强，辨识值收敛速度越快速，辨识精度则越差，从收敛速度和辨识值波动情况两方面综合考虑，选取μ 值为0.95比较理想。

2.3 电动机参数仿真实验

利用 Matlab/Simulink软件搭建仿真模型，在Simulink中进行仿真验证。当工况处于转速为30r/min，恒转矩为3N·m，选取遗传因子0.95，假设电动机参数初值为：绕组电阻2.5Ω，交直轴电感5mH，转子永磁体磁链为 0，P(0)=105I，对表 1中的PMSM电气参数进行在线辨识。其辨识结果如图8至图10所示。

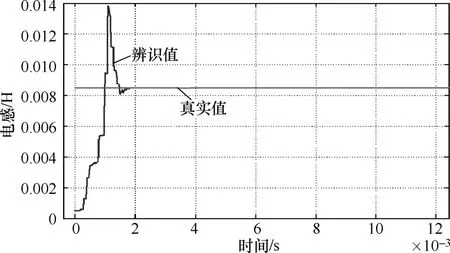
图9 交直轴电感在线辨识波形（L=8.5mH）

图10 永磁磁链在线辨识波形（ψf=0.175Wb）

由图8、图9、图10可看到：在速度和转矩恒定时，3个参数快速收敛到真实值，在不超过 0.1s的时间内，辨识出了RS、L、ψf3个参数。0.1s时辨识结果见表 2。由表 2可看出，辨识结果准确，误差很小。

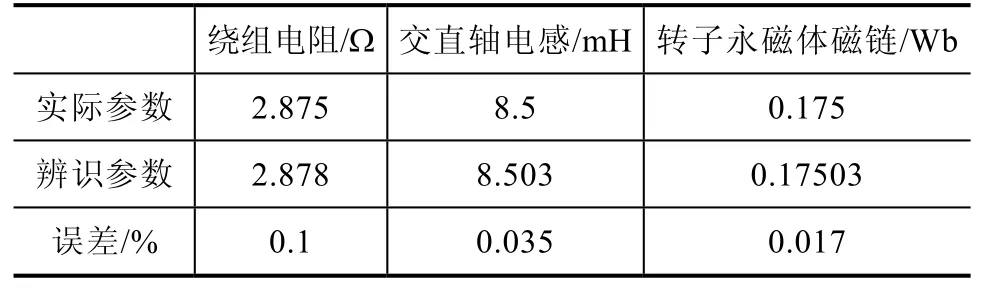
表2 辨识参数结果表

3 结论

本文在传统参数辨识的基础上提出了一种改进型的永磁电动机参数辨识算法。将FFRLS和MRAS两种算法优势相结合进行电动机参数的在线辨识。该方法能在不添加额外的激励信号的情况下把电动机电气参数一次性全部辨识出来。仿真和试验结果显示，该方法对PMSM的电气参数辨识精度较高，可有效提高辨识结果的收敛速度，具有较强的抗干扰能力，能缩短辨识时间，减少辨识动态过程振荡。实例验证了文中提出的永磁同步电动机参数在线辨识方法的有效性，具有一定的实际应用价值。

[1] 庞中华, 崔红. 系统辨识与自适应控制 MATLAB仿真[M]. 北京: 北京航空航天大学出版社, 2009.

[2] 赵金越, 关新, 胥德龙, 等. 基于模型参考自适应的电动车用永磁同步电动机无速度传感器控制系统研究[J]. 电气技术, 2017, 18(2): 36-40.

[3] 王松. 永磁同步电动机的参数辨识及控制策略研究[D]. 北京: 北京交通大学, 2011.

[4] 周虎. 永磁同步电动机参数在线辨识算法研究[D].成都: 电子科技大学, 2012.

[5] 向纯靖, 李长兵. 基于最小二乘法的永磁同步电动机参数辨识[J]. 微特电机, 2012, 40(2): 30-33.

[6] 荀倩, 王培良, 李祖欣, 等. 基于递推最小二乘法的永磁伺服系统参数辨识[J]. 电工技术学报, 2016,31(17): 161-169.

[7] 陈亚杰, 高亮. 基于混合算法的变压器参数辨识[J].电气技术, 2014, 15(1): 11-15.

[8] 杨宗军, 王莉娜. 表贴式永磁同步电机的多参数在线辨识[J]. 电工技术学报, 2014, 29(3): 111-118.

[9] 刘侃. 永磁同步电动机多参数在线辨识研究[D]. 长沙: 湖南大学, 2011: 10-37.

[10] 赵颖伟, 王毅, 李可. 基于 MRAS的改进永磁同步电动机参数辨识方法[J]. 微电动机, 2014, 47(2):29-32.

[11] Liu Kan, Zhang Qiao, Zhu Ziqiang, et al. Comparison of two novel MRAS based strategies for identifying parameters in permanent magnet synchronous motors[J].International Journal of Automation and Computing,2010, 7(4): 516-524.

[12] Wang Weihua, Xiao Xi. Research on predictive control for PMSM based on online parameter identification[C]//IECON 2012-38th Annual Conference on IEEE Industrial Electronics Society, 2012: 1982-1986.

Improved Method of On-line PMSM Parameters Identification

Shi Youji
(Tieling Teachers College, Tieling, Liaoning 112000)

A new method of on-line parameters identification of Permanent Magnet Synchronous Motor (PMSM) is proposed in this paper. The parameter identification model of PMSM in the d-q coordinate system is deduced according to the standard form of least squares method. The Forgetting Factor Recursive Least Square (FFRLS) is used to identify stator resistance value and direct axis and quadrature axis inductance value online. Based on the above identification results, the Model Reference Adaptive System (MRAS) is used to identify the permanent magnet flux linkage of the motor. The PI adaptive law based on design of Popov hyperstability theory is used to realize the on-line identification of permanent magnet flux linkage of the motor under various operating conditions. Finally, the simulation and experiment are developed with a 0.75kW PMSM as an example. The simulation results show that the proposed method in this paper has the advantages of less computation, high accuracy and better dynamic tracking performance.

PMSM；on-line identification；least squares method；MRAS

石有计（1965-），男，副教授，主要研究方向为特种电动机及其控制技术。