侧壁式气垫船峰值减阻数值研究

杨静雷，杨东梅，李平，林壮

(哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001)

侧壁式气垫船峰值减阻数值研究

杨静雷，杨东梅，李平，林壮

(哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001)

针对侧壁式气垫船在越峰过程中阻力峰值过大的问题，本文基于N-S方程，采用以多面体为核心的体网格形式，计算了其在静水中的阻力值，验证了数值计算在阻力峰值处的精确度。借助气幕减阻思想，利用一层高压高速的均匀气幕来代替传统的艏部气封装置，研究了侧壁式气垫船在气幕下的密封性能。在此基础上，数值计算了侧壁式气垫船在约束型气幕及非约束型气幕下，指端距离基线高度、喷口位置、喷口角度等气幕参数对减阻率的影响。结果表明：气幕参数的变化对减阻率影响较大，减阻率在气流量为180 m3/h时达到峰值，而最高减阻率可达到了35%；艏封采用合理的气幕形式可有效的降低侧壁式气垫船的阻力峰值。

侧壁式气垫船； 数值计算； 气幕； 减阻率； 阻力峰值； 气流量

侧壁式气垫船是在全垫升气垫船的基础上发展起来的，其特点是船体两侧采用刚性侧壁，艏艉采用柔性气封保持气垫。由于侧壁的存在，侧壁式气垫船可以运用螺旋桨或者喷泵作为推进装置，使其不仅具有良好的操纵性和航行稳定性，而且速度快，功耗低，经济性好，易于向大型化发展[1]。但由于侧壁式气垫船特殊的船艏结构，其在低速航行时艏封装置不可避免与水面接触并产生较大的推水阻力，尤其是在攀爬阻力峰阶段。侧壁式气垫船航行时，能否越过阻力峰值是设计者十分关心的问题。阻力峰值过高，会导致主机负荷增加，严重时船体会一直处于爬峰阶段，影响船舶的使用[2-3]。削减阻力峰值是提高船体越峰性能的重要手段，而艏封装置触水是引发附加兴波阻力增加阻力峰值的重要原因，改变艏封装置形式使其避免与水面接触，可以减小峰阻并能够改善船体的越峰性能。目前，国内外对侧壁式气垫船越峰性能的研究主要是从改变船体姿态和增加艉气囊让浪性两方面入手[4-6]，对于改变艏封装置形式还没有涉及。

传统的气幕减阻技术原理是利用水与空气的密度、粘度的差别, 在船底通入空气, 形成一层薄的气液两相混合流, 通过混合流密度、粘度以及流动模式的改变, 减少船体的摩擦阻力[7]。本文采用传统的数值计算方法，并借用气幕减阻的思想，在船体艏部增设一排长条形细孔，并充入高压高速气体，形成一层薄薄的气幕用于取代艏封装置，气幕一方面能够封闭气体，另一方面能够提供一定的垂向气动力矩，使船体维持一定的倾角，并保持相应的稳定性。

1 数值计算方法

1.1数值方法

对于不可压缩的粘性流动，本文采用工程应用中最广泛的Reynolds Navier-Stokes方程[7-8]，忽略密度脉动的影响，其连续性方程和动量方程如下

(1)

(2)

运动模型采用DFBI，垂向Z运动和纵向Y转动两个自由度分别对船体的垂荡运动和纵摇运动进行计算。船体重心的运动建立在整体坐标系的基础上，其运动方程如下

(3)

式中：m为质量，f为作用到船体上的各种力，ν为运动速度。而转动则是以船体重心为原点的局部坐标系建立的，其控制方程如下

(4)

式中：M为瞬时转动惯量,ω为转动船体的角速度，n为作用到船体上的合力矩。

(5)

因为张量具有对称特性，因此它可以被定义为两个向量：一个指明了对角线上的主要组成元素(Mxx,Myy,Mzz)，而另一个对非对角线上的组成元素进行了说明(Mxx,Mxy,Mxz)。

为了避免标准模型由于强旋流或带有弯曲壁面流动所造成的失真，湍流模型采用改进的Realizable模型[9-10]。计算对SIMPLE算法进行求解，PISO压力修正，并采用VOF方法进行液面处理。VOF方法[11]是运动界面追踪问题的数值模拟方法之一，它通过研究网格单元中流体和网格体积比函数F来确定自由面，从而追踪流体的变化。采用RANSE VOF求解器捕捉船体附近液体的复杂流动和喷溅效果，从而能够准确得出空气和液体的流场变化。

1.2数值模型

数值模型采用增压室式垫升系统，即高压高速气体首先进入增压室[12-13]，经过出流小孔进入气垫舱室内。船体艉封气囊采用刚性壁面，艏封囊指情况根据减阻的要求做相似的改变，如图1所示。

图1 数值模型垫升系统示意图Fig.1 Diagram of numerical model cushion

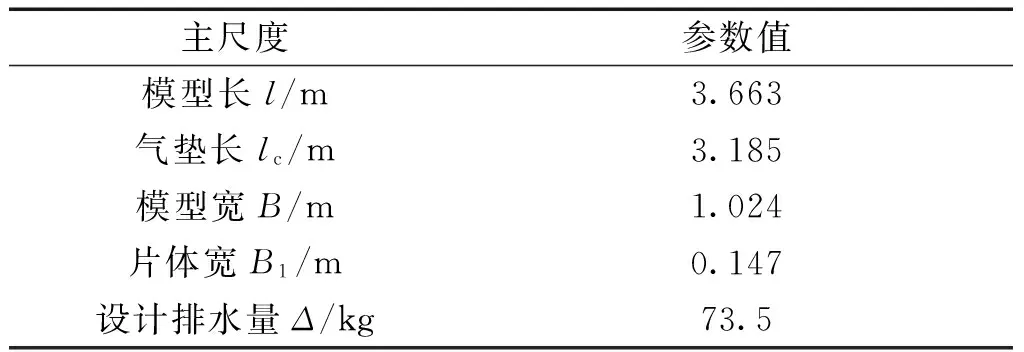
主尺度参数值模型长l/m3.663气垫长lc/m3.185模型宽B/m1.024片体宽B1/m0.147设计排水量Δ/kg73.5

网格选用以多面体为核心的体网格形式，并分别在自由液面处、船体周围以及气垫舱室进行网格加密(如图2所示)。相较于传统四面体网格，多面体网格生成更加方便快捷，且在计算效率上也要明显高于非结构化网格，在解决了交界面问题的同时，优化了网格的数量及质量[14]。根据计算经验，数值模型采用整船的形式，整个计算域网格控制在78万左右，船体表面第一层网格厚度为0.001 m，以保证y+值在50～100，以达到较好的计算精度。

边界条件采用常规船舶的CFD预报方法，计算域前方设定为速度入口并给定来流速度，后方设定为压力出口，四周界面均设定为速度入口。

图2 多面体网格形式Fig.2 Polyhedral mesh formats

1.3气幕封闭性能研究

本文采用数值计算方法，首先计算了侧壁式气垫船在刚性艏封装置下主阻力峰值处的阻力值，然后采用气幕形式代替原刚性艏封装置进行计算，最后分别与船模试验得到的阻力峰值结果进行对比，从而验证数值方法的可行性和精确度。

船模试验模型选择传统的柔性密封装置来封闭空气，艏部采用囊指式围裙，艉部采用双囊式围裙，这与数值计算采用的刚性艏封有着本质的区别。而采用气幕形式代替艏封装置是指在船体艏部甲板下缘增加一个长条形的充气孔，在此气孔处设置速度为20 m/s的恒定气流，且向内倾斜45°，形成一层出流均匀的气幕。下图为试验模型艏部柔性裙指在气垫支撑时的姿态以及气幕形式下数值计算时艏部的流场和自由液面情况。

图3 模型静垫升姿态Fig.3 Air cushion static of model

图4 气幕状态下艏部流场和自由液面情况Fig.4 The flow and free surface of bow by bubbly layer

图5为数值计算侧壁式气垫船阻力峰值处阻力值与试验结果的对比情况，其中C1为具有刚性艏封结构的数值模型计算结果，C2为采用气幕形式的数值模型计算结果，C3为试验结果。从图中可看出：刚性气封结构计算结果与试验值存在较大误差，误差值达到了13%左右；采用气幕形式代替刚性壁面结构后，计算误差明显降低，C2与试验值的误差为4.2%。

图5 阻力计算值与试验值的对比曲线Fig.5 Contrast curve of calculated and experimental values

在阻力峰值前后Fr分别为0.34和0.42时，采用气幕形式的艏封计算结果与阻力峰值处规律相同，而计算误差分别为2.5%和3.3%，因此可以看出，采用数值计算方法计算阻力峰值前后的阻力值与试验对比误差较小，可以准确的对该点处的阻力值进行预报。

图6为采用气幕形式的数值模型气垫压力分布云图，从中可以看出，在计算过程中，气垫舱室内压力保持均匀分布，而结合图4可以得到，流体域自由液面处艏部没有明显的向外出流及喷溅情况。艏部船体与自由液面之间的出流面积变化不大，整个船体运行平稳，没有出现纵摇角的突跃和升沉值的变化，因此，速度为20 m/s的恒定气流可以有效封闭气垫，并保持均匀的气垫压力。

图6 气垫压力分布云图Fig.6 The air-cushion pressure distribution nephogram

图7为该气幕形式下不同数值计算时间的艏部压力云图，从中可以看到，气垫舱室内压力除了在气幕处有稍微的下降外，向船艉移动的压力变化不大；船体前方的压力始终维持在了一个稳定的范围内，可见艏部纵向出流相对较弱，否则会导致气垫内外较大的压力突变；而在气幕内外侧出现了相对低压区，低压区范围有限，纵向宽度只有10 mm左右，同样验证了艏部出流不大的事实，同时也符合伯努利方程中有关速度和压力之和为常数的原理。

通过与无气幕时的峰值阻力计算结果对比发现，增设气幕的方式来对该侧壁式气垫船进行减阻的方法是可行的，可以用于峰值处的减阻性能研究。

对此，根据传统有关气幕减阻率的解释[15]，定义该气幕形式下减阻率η，其计算公式如下

η=ΔR/R

(6)

式中：ΔR为由于气幕引起的阻力变化，R为无气幕时侧壁式气垫船的总阻力。

2 不同气幕形式减阻性能研究

2.1约束型气幕减阻率分析

约束型气幕减阻是指通过人为改变喷口的速度形成高速高压喷射气流，得到理想中封闭气幕。通过改变艏挡板指端距离基线的高度和气流速度，对其减阻率进行研究。在试验过程中发现，气流量小于150 m3/h时，由于垫升效果不足，船体出现埋艏现场；而当气流量大于220 m3/h时，阻力变化相对较小，因此数值计算取气流量分别为150、165、180和220 m3/h。

图7 艏部压力分布随时间变化情况Fig.7 Header pressure distribution changes along time

2.1.1 指端距离基线高度对减阻率的影响

指端距离距离基线高度h设为基本变量，分别为50、90和130 mm，喷射速度设定为20 m/s，不同h的减阻率如图8所示。从图中可以看到，三种h下，减阻率呈现相似的变化趋势，均在气流量为180 m3/h左右达到最大值，减阻性能最好的一组数据最大减阻率达到35.1%，减阻效果明显；在减阻率达到最大值时，三种气流量减阻率随着基线高度的增加而加大，最大减阻率和最小减阻率之间的差值为26.7%；当气流量大于200 m3/h时，h为130 mm时的减阻率随Q的增加急剧下降，其减阻性能降到了12.5%以下，低于其他两组。

图8 不同指端高度下减阻率变化曲线Fig.8 Curves of drag reduction rate with various finger heights

2.1.2 气幕喷射速度对减阻率的影响

将气幕喷射速度V设为基本变量，分别为10、15 和20 m/s，指端距离基线高度设为130 mm，其不同喷射速度的减阻率如图9所示，从图中发现，当气流量小于170 m3/h时，随着充气速度的增加减阻率反而下降，可见，喷射速度过高不利于气幕减阻，三组曲线的减阻率在气流量为180 m3/h左右达到最大值，喷射速度为10 m/s时的减阻率与喷射速度为20 m/s峰值差别不大，两者的最大减阻率均在35%以上；喷射速度为15 m/s的减阻率明显小于其他两组数据，在减阻峰值处的最大差值达到15.4%。

图9 不同喷流速度下减阻率变化曲线Fig.9 Curves of drag reduction rate with various jet speeds

2.2非约束型气幕减阻率分析

在工程应用中，采用约束型气幕减阻形式需要单独设计一套风机管路系统对其进行气体输送，增加了设计的复杂性，可操作性不强。非约束性气幕是指在不降低减阻率的情况下，将气幕减阻的流量输送系统与垫升系统融合在一起，这样可大大降低实际工程中的应用难度，增加可操作性。非约束型气幕减阻形式将艏部喷流孔与增压室相连同而自由出流，喷射速度随垫升系统总气流量的改变而改变。非约束型气幕减阻的影响因素需要考虑船体航行姿态，喷口宽度以及距离前端的距离等。

2.2.1 喷气口纵向位置减阻率的影响

将喷气口沿纵向距离前端的距离L设为基本变量，分别为20、60和100 mm，其不同气流量下的减阻率如图10所示。从图中得到，不同气流量下的减阻率亦呈现出相同的变化趋势，即在气流量为180 m3/h处出现峰值，减阻效率达到最大。而距离前端的距离分别为20 mm和100 mm时，两者的减阻率相差不大，且均小于距离前端60 mm处的情况，相应的差值最大达到了66.1%，可见，喷口位置选择在距离前端60 mm处可得到最佳的气幕减阻率。

图10 不同喷口位置下减阻率变化曲线Fig.10 Curves of drag reduction rate with various spout position

2.2.2 喷口宽度对减阻率的影响

将喷气口宽度B设为基本变量，分别为2、4和6 mm，其不同气流量下的减阻率如图11所示。从图中发现，在主阻力峰值处，喷口宽度为2 mm时的减阻率最差，喷口宽度为6 mm时较好，两者均小于喷口宽度为4 mm时的减阻率。三者呈现出来相同的变化趋势，而喷口4 mm时的减阻率相比于喷口为2 mm时的最大差值达到了64.1%。三种不同喷口宽度的减阻率在气流量为180 m3/h时均达到了27.5%以上。

图11 不同喷口宽度下减阻率变化曲线Fig.11 Curves of drag reduction rate with various spout widths

2.2.3 喷口角度对减阻率的影响

将喷气口角度θ设为基本变量，分别为30°、45°和90°，其不同气流量下的减阻率如图12所示。从图中可得到如下结论：喷口角度θ为90°时的减阻率最好，喷口角度θ为45°时次之，喷口角度为30°时最差。而在气流量的两个极值附近，喷口角度为45°的减阻率高于喷口角度为90°的减阻率，而在气流量为180 m3/h附近时，喷口角度为45°的减阻率与喷口角度为30°的减阻率相同，但两者明显小于喷口角度为90°的数值，差值达到19%。

2.3数值计算结果分析

在主阻力峰值FrL=0.39时，以气幕的形式来代替艏封装置能够大幅度降低阻力值，其最大减阻率达到了35%。不同的气幕形式对减阻率影响较大，考虑船型姿态的影响，减阻率在气流量为180 m3/h附近达到最大。非约束型气幕可以和增压室相连同，与整个垫升系统融合在一起，降低了工程运用的复杂性，且具有较好的减阻效果，能够为改善侧壁气垫船的越峰性能提供一定的参考和借鉴。

图12 不同喷口角度下减阻率变化曲线Fig.12 Curves of drag reduction rate with various spout angles

3 结论

1)在阻力峰值处，采用气幕的形式数值计算方法代替艏部刚性气封结果能够有效降低计算值与试验值的对比误差；

2)从数值计算得到的三维速度矢量以及艏部指端处的压力云图发现，船艏处的高速喷射气流可以有效封闭垫升系统内的高压气体；

3)减阻率在气流量Q为180 m3/h时达到峰值，该气流量下采用气幕形式封闭气体可以降低侧壁式气垫船的越峰阻力；

4)与非约束型气幕形式相比，约束型气幕形式减阻效果更为有效，最大减阻率达到35.1%。

[1] 郓良.气垫船原理与技术[M] 北京：国防工业出版社, 1990： 93-97.

[2] BHUSHAN S，STERN F，DOCTORS L J. T-craft calm water resistance and motions and seekeeping in regular waves[C]//11thInternational Conference on Fast Sea Transportation(FAST 2011)，Honolulu，Hawaii， 2011： 74-81.

[3] CONNELL，BENJAMIN S，MILEWSKI，et al. Single and multi-body surface effect ship simulation for t-craft design evaluation[C]//11thInternational Conference on Fast Sea Transportation(FAST 2011)，Honolulu，Hawaii，USA， 2011： 130-137.

[4] 周伟麟，华怡，恽良. 侧壁式气垫船在波浪上纵向运动非线性理论[C]//中国造船工程学会第一届船舶耐波性会议论文集， 1979： 239-244.

[5] 邬廷芳，恽良，程炎南. 侧壁式气垫船在横浪中的横摇与升沉耦合运动[J]. 中国造船， 1987， 8(29)： 6-17.

WU Tingfang，YUN Liang，Cheng Yannan. Coupled roll and heave motions of surface effect ship in beam seas[J]. Ship building of China， 1987， 8(29)： 6-17.

[6] CLEMENTS R J， WILSON P A，LEWTHWAITE J C, et al. The potential for the use of a novel craft, pacscat (partial air cushion supported catamaran)，in inland European waterways[J]. International conference on fast sea transportation， 2005(6)： 304-312.

[7] 董文才，郭日修. 气幕减阻研究进展[J]. 船舶力学, 1998， 2(5)： 73-78.

DONG Wencai，GUO Rixiu. Research progress of air injection drag reduction[J]. Journal of ship mechanics, 1998， 2(5)： 73-78.

[8] JOHN D ANDERSON. 计算流体力学基础及应用[M]. 北京：机械工业出版社， 2007： 94-120.

JOHN D ANDERSON. Computational fluid dynamics[M]. Peking：China Machine Press， 2007： 94-120.

[9] BRIZZOLARA S. Hydrodynamic analysis of interceptors with CFD methods[C]//7th International Conference on Fast Sea Transportation. Italy， 2003： 45-56.

[10] WU Haiying，CHEN Haishan，ZENG Mingjian，et al. Analysis of the cold are effect on an extreme precipitation event triggered by inverted trough of typhoon haikui[J]. Journal of tropical meteorology， 2015， 3(21)： 211-220.

[11] HIT C W，NICHOLS B D. Volume of fluid(VOF) method for the dynamics of free boundary[J]. Journal of computational physics， 1987， 6(39)： 201-205.

[12] 李桂春，李铮捷. 气垫船气囊与气垫[M]. 北京：国防工业出版社， 2011： 156-168.

LI Guichun，LI Zhengjie. Air bag and air cushion of hovercraft[M]. Beijing：National Defense Industry Press， 2011： 156-168.

[13] LIANG Yun, ALAN B. Theory and design of air cushion craft[M]. London: Hodder Headline Group， 2000： 413-415.

[14] VILLA D，BRIZZOLARA S, VATTERONI G. CFD calculation of the hydrodynamics characteristics of planing hulls[M]. Calcoload Alte Prestazioni， 2007： 45-55.

[15] 李奇垚，董文才. 深V型船气幕减阻数值研究[J]. 海军工程大学学报, 2011， 12： 31-35.

LI Qiyao，DONG Wencai. Numerical analysis of resistance reduction by bubbly layer for deep-vee ship[J]. Journal of Naval University of Engineering, 2011， 12： 31-35.

本文引用格式：

杨静雷，杨东梅，李平，等. 侧壁式气垫船峰值减阻数值研究[J]. 哈尔滨工程大学学报， 2017， 38(11): 1709-1714.

YANG Jinglei, YANG Dongmei, LI Ping, et al. Numerical analysis of peak resistance reduction by bubbly layer for surface effect ship[J]. Journal of Harbin Engineering University， 2017， 38(11): 1709-1714.

Numericalanalysisofpeakresistancereductionbybubblylayerforsurfaceeffectship

YANG Jinglei, YANG Dongmei, LI Ping, LIN Zhuang

(College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China)

To solve the problem of a considerably large peak value surface effect ship (SES) during take-off, this study calculates the resistance of a ship in calm water using the polyhedron volume mesh based onN-Sequations and verifies the accuracy of the resistance peak. Based on the idea of reducing resistance via bubbly layer, a uniform layer comprising a high-pressure high-speed air film is used to replace the traditional header gas sealing device, and the sealing performance is then calculated. A numerical method simulates the air curtain of the SES for a binding or non-binding situation on this basis and analyzes the effect of the air curtain on the resistance reduction rate (including the height from baseline to finger, the nozzle position, and the vent angle). Results show that different air curtain parameters have vastly different effects on the drag reduction rate; the drag reduction rate reaches the peak at a gas flow of 180 m3/h and the value of the peak is 35%. Results show that the header sealing device can effectively reduce the SES resistance peak while using a reasonable bubbly layer.

surface effect ship; numerical calculation; bubbly layer; drag reduction rate; resistance peak; air flow

10.11990/jheu.201608049

http://www.cnki.net/kcms/detail/20170427.1321.008.html

U661.3

A

1006-7043(2017)11-1709-06

2016-08-23.

网络出版日期：2017-04-27.

国家自然科学基金项目(51509055，51509053).

杨静雷(1985-), 男, 博士研究生；

杨东梅(1979-), 女, 讲师,博士.

杨东梅，E-mail:yangdm411@126.com.