桥梁基础对岸坡渗透稳定及抗滑稳定性影响分析

(1.长江勘测规划设计研究有限责任公司 江河整治公司，湖北 武汉 430010；2.长江科学院 工程安全所， 湖北 武汉 430014； 3.安徽省宣城市宣州区城东防洪工程管理处，安徽 宣城 242000)

桥梁基础对岸坡渗透稳定及抗滑稳定性影响分析

郑华康1胡超2尚钦1汪继承3

(1.长江勘测规划设计研究有限责任公司江河整治公司，湖北武汉430010；2.长江科学院工程安全所，湖北武汉430014； 3.安徽省宣城市宣州区城东防洪工程管理处，安徽宣城242000)

渗透破坏是河流岸坡主要的破坏形式之一，当建设跨河流的桥梁设施时，其基础将对岸坡渗流场的分布规律产生一定影响。为了确保岸坡稳定性及长期安全运行，有必要对桥梁基础建设前后岸坡的渗流场及抗滑稳定性进行对比分析。采用三维有限元数值模拟方法对虎渡河大桥桥墩修建前后岸坡的稳定-非稳定渗流场开展了对比分析，并在此基础上采用二维极限平衡方法分析了桥梁基础对岸坡抗滑稳定性的影响。

稳定-非稳定渗流；渗透稳定性；抗滑稳定性

1 渗流有限元分析方法

堤防、岸坡的渗流场为典型的无压渗流场，属边界非线性问题。采用有限元法求解无压渗流场时，通常采用固定网格法。典型的固定网格法有剩余流量法、单元渗透矩阵调整法、加密高斯点法以及初流量法等[1～4]。这些方法的不足之处是理论不够严密，难以对渗流出渗点和自由面进行准确定位，且计算结果具有显著的网格依赖性。

Zheng等人通过将湿区中的Darcy定律延拓至全域，并将潜在溢出边界条件提为Signorini型互补边界条件，提出涵盖自由面稳定渗流问题的椭圆型变分不等式，该提法在理论上克服了溢出点的奇异性问题[5]。以此为基础，Chen等针对无压非稳定渗流问题，提出了理论上严密的抛物Signorini型变分不等式方法，并建立了基于子结构、变分不等式和自适应罚函数相结合的含复杂渗控结构渗流问题的数值模拟方法(简称SVA方法)，较为成功地解决了含排水孔幕等复杂渗控结构的稳定-非稳定渗流问题，并在实际工程应用中取得了良好效果[6]。

2 工程实例

2.1 工程概况

虎渡河大桥位于湖北省公安县，是岳阳至宜昌高速公路石首至松滋段的控制性桥梁。该桥上部引桥采用20 m装配式预应力混凝土空心板，主桥采用(68+120+68)m变截面预应力混凝土连续箱梁和50 m装配式预应力混凝土连续T梁，下部桥墩采用柱式墩或实体墩，桥台采用肋式台，桩基采用钻孔灌注桩基础。

2.2 计算模型

为精确模拟桥基修建前后堤防及岸坡中的渗流场，本文基于地质勘察资料建立了虎渡河右堤K6+940断面附近的三维有限元模型，如图1所示。该模型范围自堤轴线向堤内70 m，堤外150 m，底部高程为-20 m，模型共包括节点数为39 442，单元数为35 124，并细化了桥墩与堤基、岸坡交叉处单元网格。

图1 虎渡河右堤K6+940三维有限元模型网格

2.3 计算参数

根据地质勘查资料，各土层渗流计算参数取值如表1所示。本文中，由于自由面的下降所引起的土体压缩和弹性释放水量与自由面下降所排出的水量相比甚小，因此可以略去土体和水的压缩性，即Ss取值为零。参数μ的确定采用经验公式法，经验公式如下[7]

μ=1.137n(0.000 117 5)0.6076+lgk

(1)

图2 工况一条件下虎渡河右堤K6+940总水头等值线(桥墩修建前)(k单位为cm/s，下同)

土层名称渗透系数k/(cm·s-1)给水度μ允许溢出坡降堤身土6．68×1040．0030．50粉质粘土1．0×1060．0040．46淤泥质粉质粘土4．94×1040．0030．47粉质粘土夹砂6．79×1030．0050．44淤泥质粉质粘土2．35×1040．0030．47粉质粘土8．94×1040．0040．41粉质粘土2．62×1050．0040．38

根据地质勘察资料，各土层的物理力学指标采用试验指标建议值，如表2所示。表中所列抗剪强度均为饱和固结快剪指标。

2.4 计算工况

根据设计条件，堤防岸坡三维渗流有限元分析的计算工况及边界水位条件如表3所示。

表2 虎渡河右堤K6+940断面各土层物理力学指标

表3 渗流计算工况及特征水位条件

根据设计条件，并与三维渗流计算分析工况相对应，堤防岸坡抗滑稳定性计算工况如表4所示。

表4 抗滑稳定性计算工况及特征水位条件

2.5 渗流计算成果分析

工况一和工况三下桥墩修建前后的渗流规律见图2～5。计算结果表明，虎渡河右堤K6+940的渗流场在修建桥墩前后差距甚小，等水头线在桥墩修建前后相差不大，等水压线分布平顺，堤防岸坡内的自由面降落缓慢，并在堤脚附近逸出。

虎渡河右堤K6+940各层土体最大水力坡降如表5所示。由表5可见，桥墩修建前土体中最大渗透坡降发生在堤身土层中，其值为 0.403，小于其允许渗透坡降 0.50；桥墩修建后，各层土体最大水力坡降均有所增大，工况一条件下堤身土体最大渗透坡降为 0.441，仍小于该层土体允许渗透坡降 0.50。

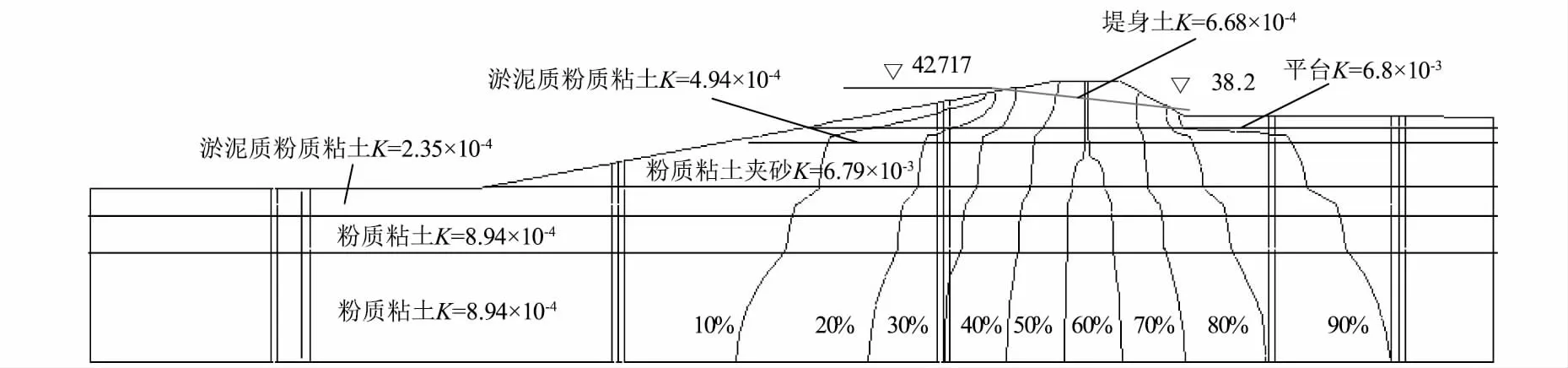
图3 工况一条件下虎渡河右堤K6+940总水头等值线(桥墩修建后)

图4 工况二条件下虎渡河右堤K6+940总水头等值线(桥墩修建前)

图5 工况三条件下虎渡河右堤K6+940总水头等值线(桥墩修建后)

桥墩修建前后，工况一和工况三条件下，堤防、岸坡均满足渗透稳定性要求。

表5 虎渡河右堤K6+940各层土体水力坡降

堤防、岸坡的非稳定渗流是由于堤外水位的变化引起的。其中，堤外水位的骤降对堤防的渗透稳定性最为不利。根据各时刻非稳定渗流场的分布规律，其最大渗透坡降及位置如表6所示。

由表6可知，渗透坡降在水位骤降1 h后达到最大值 0.673，表明水位骤降初期是最容易引起临水坡渗透破坏的时期。所以应对堤防、岸坡进行反滤保护，以保证在水位骤降时堤防岸坡也能满足渗透稳定性要求。

表6 工况二各时刻最大渗透坡降

2.6 抗滑稳定计算成果分析

由于三维极限平衡分析方法运用尚不广泛，此次堤防、岸坡抗滑稳定性分析中联合运用了二维极限平衡分析法与瑞典圆弧法。抗滑稳定计算中，选取桥墩所在剖面并将浸润线导入抗滑稳定二维计算模型；将桥墩视为混凝土材料进行考虑，未考虑其对桩周土的压密作用。

桥墩修建前，工况一和工况三条件下，堤防、岸坡背水侧抗滑稳定系数分别为1.436和1.572；桥墩修建后，工况一和工况三条件下，堤防、岸坡背水侧抗滑稳定系数分别为1.667和1.790。根据《堤防工程设计规范》(GB 50286-2013)，2级堤防土坡的抗滑稳定性不小于1.25，因此桥墩修建前后的两种工况下，虎渡河右堤K6+940均满足抗滑稳定性要求。由于桥墩阻滑作用，桥墩修建后抗滑稳定安全系数较修建前有所提高。

堤防、岸坡抗滑稳定临界滑弧如图6～7所示。

图6 虎渡河右堤K6+940抗滑稳定临界滑弧(工况一)

图7 虎渡河右堤K6+940抗滑稳定临界滑弧(工况三)

工况二条件下，将每个时刻的自由面位置作为堤防、岸坡抗滑稳定计算的水位条件，可以计算出每个时刻的安全系数。堤外侧水位 42.717 m骤降2 m，以1 m/d的速度下降，考虑堤外坡抗滑稳定。工况二的安全系数如表7所示，最小值为 2.225。可以看出，各个时段的安全系数均满足《堤防工程设计规范》(GB 50286-2013)的要求。堤防、岸坡抗滑稳定临界滑弧如图8所示。

表7 虎渡河右堤K6+940非稳定渗流各时刻的临水坡安全系数

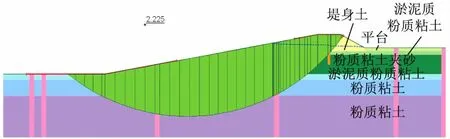
图8 虎渡河右堤K6+940抗滑稳定临界滑弧(工况二)

3 结 论

(1) 三维稳定渗流分析表明，桥基的修建对堤防、岸坡的渗流场影响较小，桥基各土层的渗透坡降最大值虽有所增大，但均在允许范围之内，堤防、岸坡的渗透稳定性可满足设计要求。

(2) 三维非稳定渗流分析表明，临水侧水位骤降时，最大渗透坡降随着时间的推移而减小，渗透坡降最大值出现在水位骤降1 h之后，临水坡渗透坡降达到 0.673。因此，堤防、岸坡的反滤防渗设计应结合实际运行条件,并考虑临水侧水位变化或骤降工况。

(3) 抗滑稳定分析表明，桥基修建后，堤防、岸坡在稳定渗流及非稳定渗流工况下，抗滑稳定系数均能满足规范要求，桥基的建设对堤防、岸坡抗滑稳定影响较小。

[1] DESAI C S, LI G C. A residual flow procedure and application for free surface in porous media[J]. Advances in Water Resources, 1983, 6(1): 27-35.

[2] BATHE K J, KHOSHGOFTAAR M R. Finite element free surface seepage analysis without mesh iteration[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1979, 3(1): 13-22.

[3] 周创兵, 熊文林, 梁业国. 求解无压渗流场的一种新方法[J]. 水动力学研究与进展, 1996, 11(5): 528-534.

[4] 张有天, 陈 平, 王 镭. 有自由面渗流分析的初流量法[J]. 水利学报, 1988, 8(1): 18-26.

[5] ZHENG H, LIU D F, LEE C F, et al. A new formulation of Signorini's type for seepage problems with free surfaces[J]. International Journal for Numerical Methods in Engineering, 2005, 64(1): 1-16.

[6] CHEN Y F, ZHOU C B, ZHENG H. A numerical solution to seepage problems with complex drainage system[J]. Computers and Geotechnics, 2008, 35(3): 383-393.

[7] 毛昶熙. 渗流计算分析与控制[M]. 北京: 中国水利水电出版社, 1990.

(编辑：朱晓红)

2017-09-15

长江口北支改善平面形态治理技术研究(2013BAB12B04);长江口北支水沙盐输运模拟技术研究(2013BAB12B03)

郑华康，男，长江勘测规划设计研究有限责任公司江河整治公司，工程师，博士.

1006-0081(2017)11-0103-04

U443.1

A