护岸工程设计基本问题浅析

2017-12-05

水利水电快报 2017年11期

(1.长江勘测规划设计研究院有限责任公司江河整治公司，湖北武汉 430010;2.宣州区城东防洪工程管理处, 安徽宣城 242000)

护岸工程设计基本问题浅析

尚钦1汪继承2周冬妮1郑华康1

(1.长江勘测规划设计研究院有限责任公司江河整治公司，湖北武汉430010;2.宣州区城东防洪工程管理处,安徽宣城242000)

由于河势演变比较复杂、护岸理论研究相对落后，且护岸工程的设计仍停留在对20世纪中早期半经验公式的应用上。通过对现行规范中基本经验公式的研究，分析了公式的适用性和局限性；在此基础上，明确了护岸工程范围的划分，阐释了护岸工程范围确定的基本原则及半定量方法，提出了工程结构(抛石粒径、防冲备填石)的设计计算方法，为护岸工程设计提供了新思路。

护岸工程；冲刷坑；防冲填石

鉴于河势演变比较复杂、护岸理论研究相对落后，且护岸设计仍停留在对20世纪中早期提出的半经验公式的应用上，导致护岸工程作为一项动态工程往往滞后于险情，且长期处在加固维护中。本文针对护岸工程设计的几个半经验公式(冲刷坑计算公式、块石抗冲粒径和防冲备填石计算公式)进行了详细研究，分析了其出处、原理和适用性，并结合当前河势演变分析手段，提出了护岸工程设计新思路。

1 半经验公式

1.1 冲刷坑计算

目前在护岸设计中广泛采用的几种冲刷坑计算公式大多引自国外有关规范标准。由于国内外水流和地质条件的不同，公式是否适用于国内河流有关问题的计算有待验证。主要的冲刷深度计算公式的来源和对比详见表1。表1中前3个公式均针对桥梁墩台局部冲刷模型，考虑水流局部流速变化、河底抗冲流速、含沙率等影响因素，并根据大量的工程案例和试验，拟合出半经验公式；后3个公式则是针对桥下冲刷模型，主要考虑由于桥墩缩小了过流断面，产生壅水，桥下河道水面比降增加，流速增大，进而导致冲刷，并根据大量工程案例拟合出半经验公式。而平顺护岸基本不改变河道过流断面，不会造成水流流场的局部变化，其近乎河床自然演变冲刷。因此上述公式不适用于平顺护岸，与丁坝的坝根冲刷也差异较大。对比各公式的计算结果，离散性较大，对于平顺护岸工程设计基本不具有指导意义。

1.2 块石抗冲粒径计算

原《堤防工程设计规范》(GB 50286-98)和《河道整治设计规范》(GB50707-2011)中均采用公式:

(1)

式中，d为块石稳定粒径，m;V为水流流速，m/s;g为重力加速度，9.81 m/s2;C为块石运动的稳定系数，水平底坡取 0.9，倾斜底坡取 1.2，《堤防工程设计规范》(GB 50286-2013)将其修订为水平底坡取 1.2，倾斜底坡取 0.9;γs为块石的重率， 2.65 kN/m3;γ为水的重率，1 kN/m3。经考证，上述公式引自前苏联时期的伊兹巴斯公式[5-6]，但是由于种种原因对稳定系数C值的引用出现笔误。块石在倾斜底坡上比在水平底坡上更易失稳，对块石粒径的要求更高，因此《堤防工程设计规范》(GB 50286-2013)的修订是正确的。目前已实施的抛石护岸工程或多或少地出现了

表1 主要冲刷深度计算公式来源和对比

抛石被冲走的现象，除河势变化、施工质量等因素外，是否存在由于错用稳定系数C值而导致设计抛石粒径偏小的情况需要作进一步探究。

伊兹巴斯公式从启动流速出发，按平抛条件推导，还是比较适用于护岸工程的，但只是笼统的按抗滑和抗倾给了两个综合稳定系数，未与岸坡坡度紧密关联，因此不够精细。

1.3 防冲备填石计算

《长江中下游平顺护岸工程设计技术要求》中对防冲石量考虑了2个方面的因素，即河道横向变形被抑制后坡脚产生冲刷需要备填石量，工程兴建后河床较长时间的调整也需要一定的加固石量，并推荐如下公式[7]。

备填石量:

(2)

加固石量计算：

Wc=KBt(∑ΔHmax-ΔHmax)/m2

(3)

式中，Wp为备填石量，m3/m;Bt为坡脚抛石厚度，m3/m；St为坡脚抛石宽度，m，重要工程取8 m，一般工程取4 m；m1为护岸前河床边坡系数，一般取0.25，m2为稳定后河床边坡系数，一般取 0.5；K1和K为安全系数，K1一般取1.1；重要工程K取1.3，一般工程取1.2；ΔHmax为从新护后第一年守护段内平均最大冲刷深度，m；据长江中下游实测资料，迎流顶冲段为5～8 m，其他守护段为3～5 m；∑ΔHmax为新护到工程基本稳定(一般为2～3 a)的累积最大冲刷深度，据长江中下游实测资料，迎流顶冲段为10～15 m，一般段为8～10 m。

根据长江中下游护岸工程经验，重要工程段防冲石量取15～25 m3/m，一般工程段取10～15 m3/m。

防冲石护岸只是经验性的工程措施，备填石量和加固石量按冲刷1 a的时间节点进行划分更是缺乏理论依据，且依据的关键参数——最大冲刷深度和第一年平均最大深度，前者来源于包尔达可夫公式，后者需待工程竣工后1 a才能获取，因此对工程设计都不具有指导意义。

2 护岸工程设计新思路

2.1 护岸工程范围的划分

传统护岸工程设计仅考虑平滩水位以下的中枯水河槽，而河床地貌应包含洪水位以下的河漫滩、平滩河槽、堤防外坡或自然阶地、山体岸坡，即整个洪水河槽，共同作用于河流的冲淤变化。考虑到洪水位以上的风浪作用区也与之存在密切关系，因此建议针对河床地貌的不同位置和作用机理，将护岸工程范围划分为护坡、护滩和护脚，分别对应洪水河床整治、中水河床整治和枯水河床整治，从而构成了护岸工程的完整体系。由于河势演变与水文情势的复杂性，实际工程难以与水位严格对应，设计中应根据具体情况灵活处理。

2.2 护岸范围的确定

近年来，利用数学和物理模型对河势演变的规律进行模拟分析取得了长足进步，因此护岸工程设计也应与时俱进，充分利用河势演变数模、物模的成果，这是今后护岸工程设计的研究方向。

2.2.1 总体布置原则

护岸工程牵涉到排涝、灌溉、航运和岸线利用等多专业问题，以及干支流、上下游、左右岸、近远期等多方面问题，极为复杂，因此如果缺少综合考虑，就不能有效处理问题。建议结合工程具体情况，总体上按照以下原则，客观、公正和科学地处理各方关系。

(1) 护岸工程布置应在防洪规划、河道整治规划(或河势控制规划)的指导下进行，统筹兼顾其他专业规划，根据工程任务，正确处理整体与局部、干支流、上下游、左右岸的关系，应先重点后一般，远近结合，分期实施。

(2) 在规划方案确定后，护岸工程总体上要根据河势演变的数模、物模成果确定。

(3) 护岸范围应根据近岸流速分布、地质情况、历史地形套绘定量分析确定。

(4) 应根据保护对象、工程影响等因素进行修正和优化。

(5) 需考虑工程实施后对上下游、对岸、河底的影响，并制定相应的处理方案。

(6) 要考虑未来一定时期内可能的河势变化，护岸位置和范围要留有一定的安全裕度。由于护岸工程的复杂性，建议有关主管单位在工程竣工后安排工程后评价，由相关单位针对(4)和(5)中的问题进行补充设计和工程处理，该部分费用应包含在整个工程投资中。

2.2.2 确定护岸范围的半定量方法

以往护岸范围确定主要依据险情调查、近年河道地形套绘、冲刷坑计算以及工程经验，存在一定的不确定性和局限性：未出险的河段不表示在其他水流条件下就一定稳定，出险河段也可能从此稳定，甚至开始淤积；依据近年河道地形套绘，可发现河床地貌的变化，可信度相对较高，但由于河势演变的复杂性，河床地貌年内年际发生较大变化也属正常，当缺乏测量资料时也易作出误判；冲刷坑计算公式本身存在局限性，工程设计人员的主观判断随机性较大；因此，通过比较各种水流条件下(至少应包括代表性的枯水位、中水位和洪水位)近岸流速和岸坡土体不冲流速的分布情况，从泥沙起动条件着手，由定量确定可能冲刷范围的结果更加可信，这相当于在定床条件下来判定冲刷可能。同时为了弥补定床模型的不足，仍需结合历史地形资料套绘综合确定。把历史套绘资料、数模成果、流速比较成果统一在一个平台上分析，将影响因素量化，尽可能消除工程设计中主观因素的影响。

2.3 工程结构设计方法

2.3.1 抛石粒径计算方法

1979年，Stephenson推导了与伊兹巴斯公式基本相同的公式[6]，并分别按平抛、立抛给出了考虑护岸材料水下天然休止角和岸坡坡角因素的综合稳定系数K的计算公式：

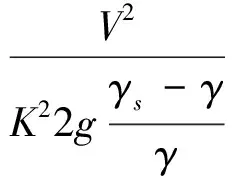
(4)

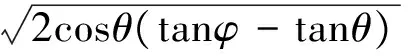
(5)

式中，V为抛石稳定部位的垂线平均流速，m/s;K为综合稳定系数；θ为边坡坡度，φ为抛石休止角。按《堤防工程设计规范》(GB50286-2013)推荐公式计算，斜坡上的块石计算粒径是水平底坡的1.78倍，这直接影响了抛石厚度和工程投资。未考虑岸坡坡度的设计过于粗糙，且很多设计人员并不了解规范公式的出处和原理，造成伊兹巴斯公式长期被错用，因此推荐采用Stephenson公式。实际工程中，水下护岸大多采用块石，通常天然休止角基本接近42.5°，岸坡坡比一般在1∶1.5～1∶10之间。该公式并不复杂，但由于缺乏块石材料，其他护岸材料开始逐步推广，因此有必要根据岸坡坡角和护岸材料水下天然休止角进行优化设计。按Stephenson公式计算K值的相关分析如表2所示。

表2 平抛护岸形式综合稳定系数K值

平整、均匀的坡式平顺护岸，护岸材料接触面为自然岸坡，滑动比滚动容易，综合稳定系数K可以采用平抛公式计算；丁坝等坝式护岸或起伏较大的坡式护岸，上部表面护岸材料与下部同类型材料互相嵌填、咬合，不易产生滑动，控制条件以抗倾稳定为主，因此可采用立抛公式计算。

工程实际中抛石护岸坡比一般不陡于1∶2，从表2可以查得K=0.86。抛石护岸一般护至岸坡坡比1∶4时，可以查得K=1.14，与《堤防工程设计规范》(GB50286-2013)推荐公式水平K=1.2、倾斜K=0.9的成果范围大致相当。

2.3.2 防冲备填石计算方法

防冲备填石的概念来自于工程经验，如果可能受到冲刷部位已得到防护，或者已经对其采取全断面防护，那么防冲备填石就失去了其存在的意义，实际工程经验也表明以往工程护岸范围的设定还需斟酌。

实际工程中，由于工程需要、投资限制、河势变化等原因，护岸范围难以完全覆盖可能冲刷区域，此时设置一定的防冲备填，很有必要进一步观察，尤其在一些允许枯水河槽适度冲刷的护滩工程中。由于备填石和加固石的划分并不严格，对工程设计也没有意义，建议不再细分，只需保留防冲备填石一个概念即可。

如假设K1=K，将公式(1)和(2)相加，得到下述公式：

W=KBt[∑ΔHmax-St(m2-m1)/m2

(6)

假设抛石满布坡面，总防冲石量近似于冲刷前后坡面的护岸抛石量之差,见图1。

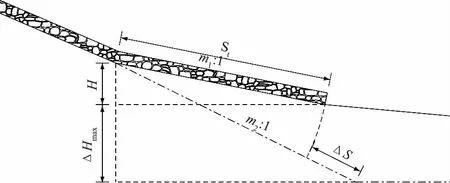
图1 防冲备填石计算

根据图1，可推导出防冲备填石量计算公式如下

(7)

式中，K为综合稳定系数，Bt为坡脚抛石厚度，m3/m;ΔS为坡脚冲刷前后抛石宽度，m;ΔHmax为新护后第一年守护段内平均最大冲刷深度，m;St为坡脚抛石宽度，m;m1、m2分别为护岸前和稳定后的河床边坡系数。

按此公式计算，长江中下游护岸工程的重要工程段防冲石量为24～39 m3/m，一般工程段取19～24 m3/m，总体上大于公式(5)计算成果。影响较大的主要是ΔHmax的取值，该值不能简单地由包尔达可夫公式计算求得，应由河势演变和冲淤计算综合确定，当防护范围足够大，河床不能再进一步淘刷，冲刷深度可取零。根据上述公式，当W计算值不大于零时，说明防护范围已可抵抗可预见的坡脚冲刷。