码头群密度及非均匀度对近岸区洪水动力特性的影响研究

(1.长江勘测规划设计研究有限责任公司 江河整治公司，湖北 武汉 430010；2. 鄂州市河道堤防管理处，湖北 鄂州 436000)

码头群密度及非均匀度对近岸区洪水动力特性的影响研究

江磊1芦伟宏2胡春燕1侯卫国1陈前海1陈正兵1

(1.长江勘测规划设计研究有限责任公司江河整治公司，湖北武汉430010；2.鄂州市河道堤防管理处，湖北鄂州436000)

目前，码头群叠加对近岸水动力变化叠加影响的认识尚不清楚，研究码头群的叠加效应对于指导工程实践和优化港区布局具有重要意义。采用资料分析和数值模拟相结合的方式，以南京河段新济洲左汊左岸七坝港区为研究对象，分析了量化码头群数量和码头群排列方式的指标，选择不同的量化指标模拟分析了码头群密度及码头群非均匀度对近岸洪水动力特性的叠加影响。结果表明，水位流速变化幅度及影响范围与码头群密度正相关，近岸水位壅高降低及流速增大减小的位置与码头群密度无关，但幅度随码头群密度的增大而增大；码头群非均匀度的影响与码头群密度不同，水位流速变化幅度及影响范围随非均匀度先增大后减小，近岸水位壅高降低与流速增大减小位置随码头群非均匀度先增大后减小。码头群密度对水流特性的影响较码头群非均匀度大，在实践过程中应控制码头群的密度。

码头群密度；非均匀度；洪水流量；叠加影响

河道内码头修建占用过水面积、增大局部阻力，导致局部水位壅高、流速增大，影响防洪安全并危及堤防稳定。由于高桩码头对各类型的地基具有较强的适应性，因而成为我国广泛使用的码头结构形式之一[1]。随着国民经济发展，城市河道人类活动加剧，岸线开发利用程度增加，大量涉河工程的兴建导致河道内水位流速较天然河道更为多变，防洪形势更加复杂[2]。城市局部河段内由于水深条件好，通常码头连片布置，较短的岸线内存在数个码头，形成码头群。码头群的存在可能会导致水流运动条件下码头间叠加或遮蔽效应的产生，使其对水流运动特性的影响较单个码头更为明显、复杂，也进一步加剧了防洪的安全隐患[3]。因此研究码头群的影响在丰富研究体系方面具有一定理论意义，而在保障防洪安全方面具有较大实际意义。

大量研究者对单个码头或单块桩群对水流结构的影响进行了深入研究[4]。单个码头对水流结构的影响主要表现为码头上游水位壅高、两侧流速增大，但对水位流速影响范围较为有限[5-6]。单块桩群对水流影响主要与桩群形状、桩群密度、桩群宽度及长度有关，桩群密度越大，桩群宽度则越宽；桩群长度越长，其对水流的影响越大[7-9]。目前少有研究涉及到码头群或桩群块联合体对水流的影响。码头群对水流的影响的研究主要涉及以下两个问题：①如何量化码头群，应采用何种指标对码头数量、排列方式进行定量描述？②不同量化指标条件下码头群对水流结构，尤其是对洪水水流结构有何影响？

本文以南京河段新济洲左汊七坝港区为研究对象，采用平面二维水流数学模型研究了码头群对洪水水流结构的影响，研究内容主要包括：①码头群密度及排列方式量化指标初探；②码头群密度对洪水动力特性的影响；③码头群排列方式对洪水动力特性的影响；④码头群密度及非均匀度对洪水动力特性影响的比较分析。

1 数值模型建立及研究工况

1.1 基本控制方程

本文通过二维水流数学模型模拟研究码头群对区域水动力特征的叠加影响，区域水动力特征变量(水位、流速、近岸水位流速等)通过求解水深平均的平面二维水流运动方程组得到。控制方程组的表达形式为

(1)水流连续方程：

(1)

(2)水流动量方程：

(2)

(3)

式中，u、v分别为垂线平均流速在x、y方向上的分量，m/s；h为总水深，h=η+d，d为静止水深，η为水位，m；g为重力加速度，m/s2；τsx、τsy分别为表面切应力分量，N/m2；τbx、τby分别为底部切应力分量，N/m2；ρ为水的密度，ρ0为参考水密度，kg/m3；f为Coriolis参数(Ω为地球自传角速度，Φ为地理纬度)，f=2ΩsinΦ；fv和fu分别为地球自传引起的加速度，m/s2；Sxx、Sxy、Syx、Syy为辐射应力分量，N/m2；Txx、Txy、Tyx、Tyy为水平粘性应力项，N/m2。

Tij横向上包括粘滞摩擦、动荡摩擦和差别平流项。对这几项的估测使用的是一种基于水深平均流速梯度的涡粘性公式：

(4)

式中，vs为涡粘系数，m2/s。

1.2 方程离散及求解

采用三角网格对计算区域进行离散，对重点研究区域进行加密处理。在离散区域的三角形控制单元上，首先对方程组(1)～(3)进行积分，将方程离散为3部分，即时间积分项、空间积分项和源项积分项。时间积分项和源项积分项可直接利用显式方法求解。空间积分项的求解是关键，首先利用高斯公式将面积分转化为线积分，线积分即为单元边处的界面数值通量。界面数值通量有多种算法，本文模型采用求解法向一维Riemann问题的方法来计算界面数值通量。大量理论及实践研究表明此方法在求解河道水流运动时具有较高的精度和稳定性。

1.3 模型率定与验证

本文所建模型范围上起彭心洲洲头、下至大胜关，长度约为55 km。采用2011年8月实测的水位和流速分布验证数学模型，验证内容包括新济洲左右汊水面线及左右汊内的流速分布。验证结果表明，模拟计算水面线与实测水面线吻合度较高，模拟计算流速大小及分布形态与实测流速大小及分布形态较吻合，误差满足计算精度的要求，说明模型能较好地模拟新济洲河段的水流运动。

1.4 码头阻水特征分析

防洪设计洪水条件下，高桩码头的阻水建筑物主要包括前沿平台：横梁、纵梁及桩基，平台、横梁、纵梁合称为上部结构，桩基称为下部结构，下部结构是上部结构的支撑建筑物。数学模型中以桩基为基本单元将码头概化为桩群，桩群中单个桩的下部为圆柱结构，上部为立方体结构。大量统计分析结果表明码头各细部结构占用过水面积的比率A平∶A横∶A纵∶A桩为1∶0.379∶2.5∶8.533。由此可见，码头的主要阻水建筑物为下部桩基。模型中桩群的阻水效果主要通过增加局部网格的阻力实现，阻力大小等于水流中障碍物的绕流阻力，其计算表达式为

F=0.5ργCDAeV2

(5)

式中，F为单个桩在水流中的绕流阻力，N；γ为桩的形状系数，实际计算过程中根据不同的形状取值；CD为拖拽力系数；Ae为桩的有效阻水面积，m2;V为水流的平均流速，m/s。

1.5 码头群量化特征分析

港区内码头群通常顺岸布置、呈带状分布，因此码头群的特征主要体现在沿河道的纵向上。目前尚无较好的量化指标来综合反映码头群的纵向特征。码头群纵向特征的量化主要涉及两个问题：①如何在固定长度岸线内量化码头数量；②固定码头数量条件下，如何量化分析码头排列方式差异。针对上述两个问题，在分析长江南京河段左右岸码头分布特性的基础上，本文提出了如下两个指标。

(1)码头群密度系数σ。码头群数量的多少对水流运动特性的影响可能存在明显差异。码头群密度系数σ主要用来定量描述河段内码头群数量，其定义为岸段内码头平台前沿线长度累加之和与岸线总长度的比率，表达式为

(6)

式中，li为第i个码头的平台前沿线长度，m；L为岸线的总长度，m。由上式可知，密度系数σ克服了天然河道内码头零碎、尺度大小不一，难以统计量化等缺点，是较好的天然河道码头建设密度量化指标。σ的取值范围为[0，1]，当研究岸段内无码头时，σ为0；当研究岸段码头无间距全排列时，σ为1。

(2) 码头群非均匀度系数ε。在河道某一岸段内码头群数量不变的条件下，码头群顺岸存在多种排列方式，不同排列方式对水流特性可能存在不同的影响。码头群非均匀度系数ε主要用来定量描述河段码头群排列方式的差异，其定义为岸段内相邻两码头的最小间距dmin与最大间距dmax的比率。由于在dmin及dmax确定的条件下，dmin及dmax相对于水流流向存在两种位置关系，即dmin在上游、dmax在下游和dmin在下游、dmax在上游。这就导致对于同一个ε值，依然存在两种不同的码头群排列方式。因此附加定义当dmin位于上游时，ε值取为正；dmin位于下游时，ε值取为负，具体表达式为

(7)

式中，dmin为岸段内相邻码头的最小间距，m；dmax为岸段内相邻码头的最大间距，m。由上式可知，ε的取值范围为[-1,1]。当岸段内码头均匀排列时，ε为1；当岸段内相邻码头搭界时，ε为0；当岸段码头接近于均匀排列且dmin位于下游时，ε→-1。

1.6 研究工况

本文选取南京河段新济洲左汊左岸七坝港区为研究对象，选定岸段岸线长度约为3 500 m。现状条件下共有4个码头，码头密度系数σ为0.246，码头非均匀度系数ε为0.199。设定两种典型情况分别将研究码头群密度、码头群非均匀程度对水流结构的影响。典型情况1为码头群密度影响水流研究。在现状码头密度条件下，分别将密度减小和增大1倍，形成3种工况，各工况码头均匀排列，非均匀度系数均为1.0(见表1)。典型情况2为码头群非均匀度影响水流研究。在均匀排列码头条件下，调整码头位置形成3种工况，各工况码头数量相同，密度系数均为0.212(见表2)。

表1 码头密度影响水流的计算工况

表2 码头非均匀系数影响水流的计算工况

2 计算结果分析与讨论

2.1 码头群密度影响

(1) 局部水位流速变化。码头兴建后，由于占用了过水面积且阻力增大，水位变化主要发生在上游区域，以壅高为主；流速变化则较多发生在下游区域，主要表现为流速的减小。表3为局部区域内水位最大壅高△Hmax及流速最大减小△vmax随码头群密度σ的变化。由表3可知，△Hmax及△vmax随σ的增大而增大，表明随着码头群密度的增加，水位壅高及流速减小产生了明显的叠加效应。△Hmax及△vmax随σ的增加总体呈线性增长趋势，因此采用线性模型对数据进行拟合：△Hmax与σ的线性斜率系数k=11.64，回归系数R2=0.97；△vmax与σ的线性斜率系数k=8.16，回归系数R2=0.89。由此可证明码头群密度对水位壅高幅值的影响更明显。

表3 水位最大壅高及流速最大减小随码头密度的变化

图1为局部区域水位壅高1.0 mm等值线随码头群密度σ的变化图，图2为局部区域流速减小2.0 cm/s等值线随码头群密度σ的变化图。由图1可知，水位壅高影响的区域大小S1及流速减小影响的区域大小S2亦随码头群密度σ的增大而增大：当σ=0.123时，S1=0.99×104m2；当σ=0.246时，S1=21.87×104m2；当σ=0.492时，S1=206.53×104m2。当σ=0.123时，S2=15.89×104m2；当σ=0.246时，S2=57.40×104m2；当σ=0.492时，S2=62.35×104m2。由此可见，码头群密度对水位壅高范围的影响较流速减小范围的影响更明显。

图1 不同密度条件下水位壅高1 mm等值线

图2 不同密度条件下流速减小2 cm/s等值线

(2) 近岸水位流速变化。图3为近岸水位变化△H随码头群密度σ的变化图，图4为近岸流速△v变化随码头群密度σ的变化图(图中x为自上游向下游的距离)。从图3～4可知，近岸水位流速的变化幅度小于局部区域水位流速的变化幅度。码头密度对最大水位壅高(△Hmax)和降低(△Hmin)、最大流速增大(△vmax)和减小(△vmin)位置无明显影响，但对其幅值影响显著。当σ=0.123时，△Hmax=0.55 mm，△Hmin=-0.75 mm；当σ=0.246时，△Hmax=1.00 mm，△Hmin=-2.40 mm；当σ=0.492时，△Hmax=1.80 mm，△Hmin=-4.65 mm。当σ=0.123时，△vmax=0.80 cm/s，△vmin=-0.60 cm/s；当σ=0.246时，△vmax=2.00 cm/s，△vmin=-4.00 cm/s；当σ=0.492时，△vmax=4.50 cm/s，△vmin=-8.00 cm/s。由此可见，随着码头密度增大，近岸水位流速基本呈线性增长趋势。

图3 不同码头密度条件下近岸水位变化

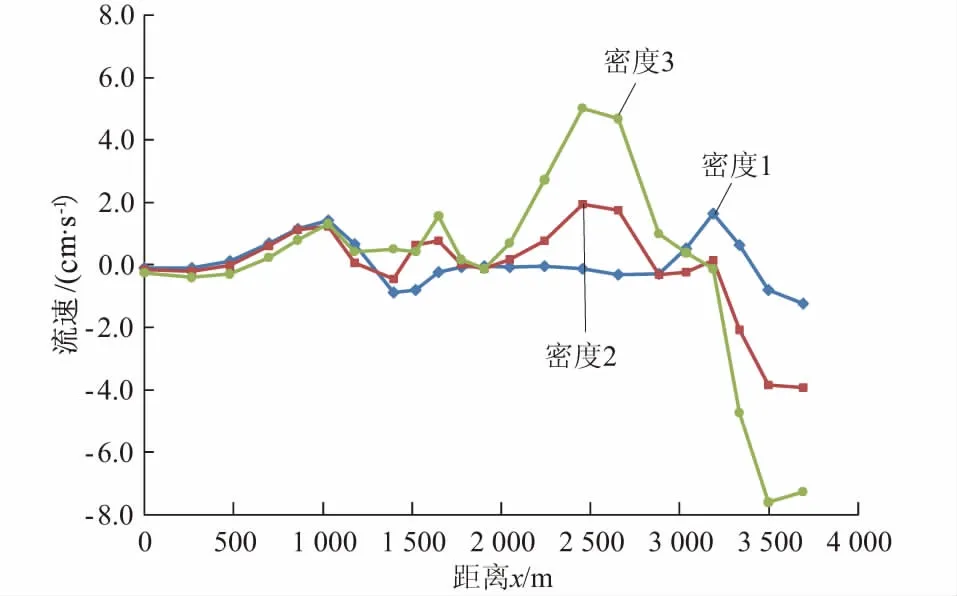
图4 不同码头密度条件下近岸流速变化

2.2 码头群非均匀度影响

(1) 水位流速变化。码头群非均匀度变化主要改变码头的排列方式，非均匀度值绝对值越小，码头群排列越不规则。表4为局部区域内水位最大壅高△Hmax及流速最大减小△vmax随码头群非均匀度ε的变化。从表4可知，△Hmax及△vmax随ε的增大呈先增大后减小的变化趋势，说明水位壅高及流速减小与码头群非均匀度并非是单一的关系。△Hmax及△vmax随ε增加无明显的变化趋势，采用线性模型对数据进行拟合：△Hmax与σ的线性斜率系数k=0.71，回归系数R2=0.35；△vmax与ε的线性斜率系数k=0.31，回归系数R2=0.12；由此可见，码头群非均匀度对水位壅高及流速减小影响不明显。

图5为局部区域水位壅高1.0 mm等值线随码头群非均匀度ε的变化，图6为局部区域流速减小2.0 cm/s等值线随码头群非均匀度ε的变化图。从图5～6可知，水位壅高影响的区域大小S1随码头群非均匀度ε的增大呈先增大后减小的变化趋势，当ε=-0.334时，S1=3.06×104m2；当ε=0.334时，S1=17.15×104m2；当ε=1.000时，S1=3.22×104m2。流速减小影响的区域大小S2随码头群非均匀度ε的增大基本保持不变，当ε=-0.334时，S2=43.7×104m2；当ε=0.334时，S2=47.40×104m2；当ε=1.000时，S2=42.35×104m2。由此可见，码头非均匀度对水位壅高范围的影响较流速减小范围的影响更明显。

表4 水位最大壅高及流速最大减小随码头非均匀度的变化

图5 不同非均匀度条件下水位壅高1 mm等值线

图7 不同非均匀度条件下近岸水位变化

图8 不同非均匀度条件下近岸流速变化

(2) 近岸水位流速变化。图7为近岸水位变化△H随码头群非均匀度ε的变化图，图8为近岸流速△v变化随码头群非均匀度ε的变化图(图中x为自上游向下游的距离)。从图7～8可知，近岸水位流速的变化幅度小于局部区域流速的变化幅度。近岸水位的变化趋势依然是上游壅高下游减小，最大水位壅高(△Hmax)随ε的增加呈现先增大后减小的趋势，最大水位降低(△Hmin)随ε的增加呈现先减小后增大的趋势。当ε=-0.334时，△Hmax=0.70 mm，△Hmin=-2.20 mm；当ε=0.334时，△Hmax=1.10 mm，△Hmin=-1.90 mm；当ε=1.000时，△Hmax=0.80 mm，△Hmin=-2.1 mm。近岸流速的变化较为复杂，ε既影响流速变化的位置也影响流速变化的幅度。最大流速增大(△vmax)随ε的增加先减小后增大，最大流速减小(△vmin)随ε基本保持不变位置。当ε=-0.334时，△vmax=0.60 cm/s，△vmin=-3.20 cm/s；当ε=0.334时，△vmax=1.40 cm/s，△vmin=-3.15 cm/s；当ε=1.000时，△vmax=0.60 cm/s，△vmin=-3.20 cm/s。由此可见，码头非均匀度对近岸水位的影响较流速的影响更明显。

相邻码头最小间距dmin出现的位置可能是码头非均匀度影响呈先增大后减小的重要原因，对于ε=-0.334和ε=0.334两种工况，尽管非均匀度绝对值大小相同，但两者的差别主要体现在：当ε=0.334时，dmin位于上游；当ε=-0.334时，dmin位于下游，上游码头群可能对下游码头群的影响产生了明显的屏蔽效果。为验证此设想，将码头群密度影响和码头群非均匀度影响的计算结果进行统一分析，统计各工况上游区域码头最小间距dmin，由于工况ε=-0.334条件下dmin位于下游区域，因此用最大间距dmax代替上游区域的最小间距dmin。对上游区相邻码头最小间距dmin与局部最大水位壅高△Hmax的关系进行统计，并画图进行回归分析(见图9)。从图可知，随dmin增大，△Hmax逐渐减小，两者呈现明显的负相关关系，采用幂指数函数进行回归，回归系数R2=0.815 1。这也进一步说明码头群非均匀度对水流的影响主要与上游区相邻码头的最小间距有关。

图9 上游区最小码头间距与最大水位壅高关系

3 结 论

(1) 洪水动力特性变化与码头群密度正相关，局部水位最大壅高及影响范围、局部流速最大减小及影响范围、近岸水位流速增大减小均随码头密度的增大而增大。

(2) 当相邻码头最小间距位于上游时，洪水动力特性变化与码头非均匀度负相关，局部水位最大壅高及影响范围、局部流速最大减小及影响范围、近岸水位流速增大减小均随码头群非均匀度的增大而增大。

(3) 当相邻码头最小间距位于下游时，局部水位最大壅高及影响范围、局部流速最大减小及影响范围、近岸水位流速增大减小均随码头群非均匀度的增大保持不变。

(4) 码头群密度对洪水动力特性的影响较码头群非均匀度大，在实践过程中应更注意控制岸线内的码头密度。

[1] 黄本胜，程香菊，袁丽蓉，等. 码头桩群对河道行洪与流场影响的三维数值模拟[J]. 水动力学研究与进展A辑，2010,25(1)：99-105.

[2] 吴飞. 高桩码头桩群对河道水流特性影响的数值模拟研究[J]. 水资源与水工程研究，2008年，2008,19(1)：89-93.

[3] 李彬，刘博，郑国栋. 码头群连体扩建对河道水流影响的数值模拟[J]. 广东水利水电，2016(6)：1-3.

[4] 李文文，黄本胜，候杰. 高桩码头桩群水流特性的试验研究[J]，新疆农业大学学报(自然科学版)，2004，27(4)：78-81.

[5] 王春华. 高桩码头桩群对流场及底床影响试验研究[D]. 南京:南京水利科学研究院, 2010：30-35.

[6] 李光炽，周晶晏，张贵寿. 高桩码头对河道流场影响的数值模拟[J]. 河海大学学报(自然科学版)，2004,32(2)：216-220.

[7] Stephen E. Coleman. Clearwater local scour at complex piers[J]，Journal of Hydraulic Engineering，2005，131(4)：330-334.

[8] Siniscalchi F, Nikora V I, Aberle J. Plant patch hydrodynamics in streams: mean flow, turbulence, and drag forces.[J] Water Resources Research, 2012, 48 (1): 1513-1519.

[9] Rominger J, Nepf H M. Flow adjustment and interior flow associated with a rectangular porous obstruction.[J] Journal of Fluid Mechanics, 2011, 680: 636-659.

(编辑：李晓濛)

2017-09-15

国家重点研发计划课题(2016YFC0402306)

江 磊，男，长江勘测规划设计研究有限责任公司江河整治公司，工程师.

1006-0081(2017)11-0047-06

TV131.2

A