基于PI控制和重复控制的有源电力滤波器研究
2017-12-05汪鹏朱卫海王伟向真廖敏夫
汪鹏 朱卫海 王伟 向真 廖敏夫
(1.深圳供电局有限公司 2.大连理工大学)
基于PI控制和重复控制的有源电力滤波器研究
汪鹏1朱卫海1王伟1向真1廖敏夫2
(1.深圳供电局有限公司 2.大连理工大学)
本文主要针对并联型有源电力滤波器的控制算法进行了研究,分别从PI控制和重复控制的结构、原理、控制算法和MATLAB仿真分析,对比了静态补偿特性和动态响应特性的控制效果,得到重复控制具有较好的静态特性,但无法快速响应系统的动态变化;而PI控制动态响应效果好,但无法进行无静差跟踪。因此提出了基于PI控制和重复控制的综合控制算法,并通过MATLAB建立了仿真模型进行了仿真分析,仿真结果表明:基于PI控制和重复控制的综合控制,既可通过重复控制来改善补偿精度,又可利用PI控制加快响应速度,验证了该方案的可行性,为高精度、高可靠性并联有源电力滤波器控制奠定了基础。
有源电力滤波器;PI控制;重复控制
0 引言
随着电力电子技术的快速发展,电力电子设备和非线性、冲击性负荷的广泛运用,造成电力系统谐波污染日趋严重[1],谐波治理也变得越来越重要。传统的谐波补偿方法是装设无源滤波装置,因其既可消除谐波,又可以补偿无功,且结构简单、安装方便、成本较低[2]。但无源滤波装置存在许多自身无法克服的缺点:体积大,只能消除特定次谐波,补偿效果受电网阻抗及运行状态影响,易与系统阻抗产生谐振,故补偿效果不够理想[3-4]。与无源滤波器相比,有源电力滤波器(Active Power Filter,APF)在传统的谐波治理装置中被认为是谐波治理、无功补偿、改善电能质量最有效的装置之一[5]。其能够补偿无功和各次谐波、具有灵活柔性控制策略和良好的动态补偿特性,补偿主动及时、抑制谐波的频谱宽、对系统参数变化有良好的鲁棒性,因此成为了谐波抑制的主要趋势[6-9]。其原理是从负载中检测出谐波分量,通过控制逆变器产生一个与谐波电流互补的补偿电流,以抵消系统中的谐波分量,从而达到消除谐波的目的[10-12]。目前,并联型有源电力滤波器是最基本、应用最为广泛的有源电力滤波器类型,其主电路结构已比较稳定,因此性能很大程度依赖于控制系统的设计。
APF常用的控制方法有自适应控制、PI控制、重复控制、神经网络控制、滑模控制等[13-15]。本文以采用d-q检测法检测谐波电流为前提,在控制环节通过对PI控制与重复控制方式原理及仿真结果的分析,提出了将二者并联使用的复合控制方案。
1 PI控制器的设计与仿真
PI控制作为一种经典的控制方法[16],具有结构简单、动态响应性好、调试方便、鲁棒性强等优点[17-19]。下面将就电流环及电压环PI控制器进行设计。
1.1 电流环PI控制器的设计
在电流检测环节,本文默认已采用d-q检测法。由于经过变换后,系统的d、q轴间会引进一些交叉耦合项,可采用状态反馈解耦法将交叉耦合项的作用消除,以实现对d、q轴电流的独立控制。解耦后,根据PI控制的方法,电流控制框图如图1所示。

图1 d-q坐标系下电流控制框图
图1中,虚线左侧为控制器,右侧为被控对象。由图可发现d轴和q轴的形式与结构一样,故可先对一个轴进行设计。
选取d轴为研究对象,假设输出电压不饱和,通过解耦运算,得到的电流环简化框图如图2所示。
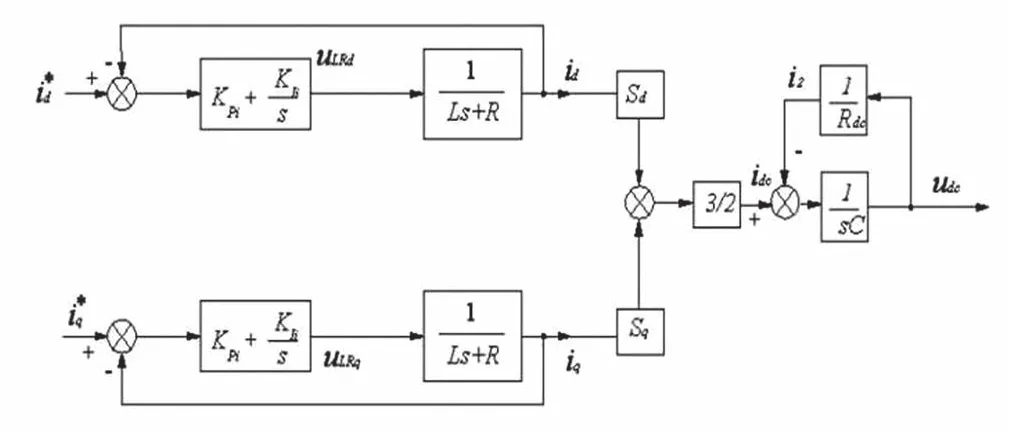
图2 d-q坐标系下电流控制简化框图
由图2可得开环系统的传递函数为:

易得其闭环传递函数为:

根据零点-极点对消法,将闭环系统降为典型的一阶惯性系统,即令 KIi= RKpi/L,带入式(2)可得一阶传递函数如下:

其中,

式中, Td为电流闭环系统中电流响应的惯性时间常数,该系统的截止角频率为ωd=1/Td,其值越大,响应越快,跟踪性越好。在本次设计中,DSP的采样频率取为6.4kHz,电感值取1mH,代入以上各式可得理论控制参数: Kp=8~15,K1=400~670。
1.2 电压环PI控制器的设计
在APF结构中,三相逆变电路的直流侧电压源通常用一个电容来代替。APF工作时,电容电压的波动将会影响补偿电流,进而影响最终的补偿效果,因此,对该侧电压进行闭环控制也十分有必要。
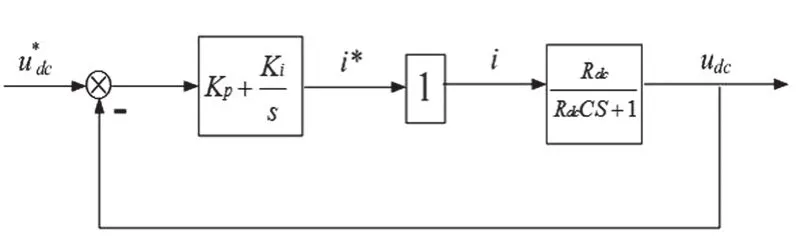
图3 电压环控制结构图
由图易得其开环传递函数为:

该系统应满足:

将式(6)代入式(5),可得闭环传递函数为:

式中,τ为系统的惯性时间常数,其值大小将影响系统响应速度的快慢。
1.3 仿真分析
为了验证上文所提出的PI控制器可行性,现用Simulink进行仿真。其主电路及控制电路分别如图4和图5所示。控制电路模块里的PI控制部分如图6所示。

图4 主电路整体模块
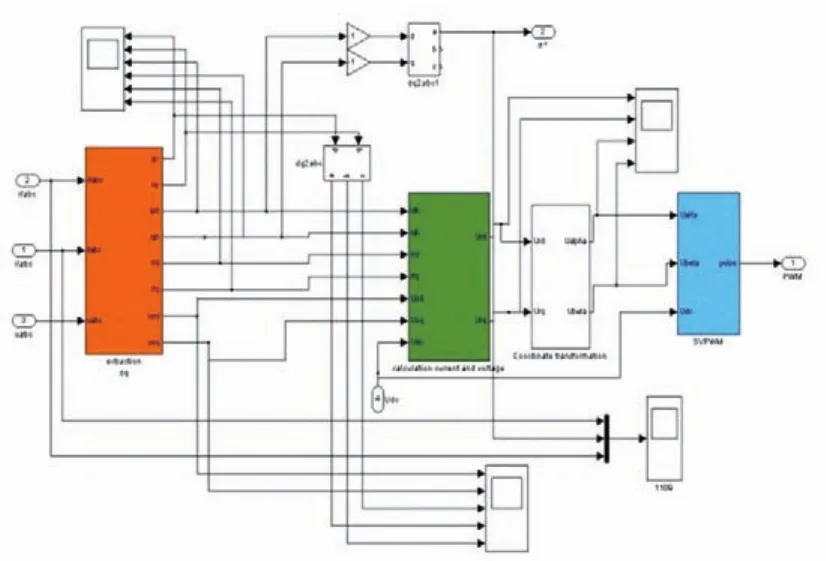
图5 控制电路模块
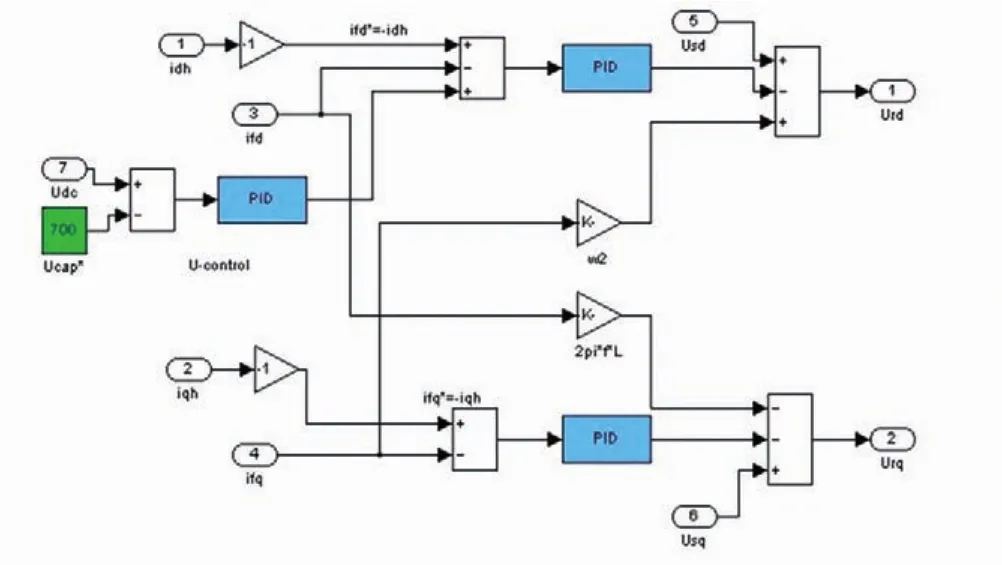
图6 控制电压和指令电流模块
综合考虑各参数之间的相互关系,设定以下参数:交流电网的接线方式为对称三相星形接线,频率50Hz。直流侧采用2mF的电容,其正常工作状态下稳定电压为700V,交流侧的滤波电感取值为0.7mH。谐波源为带阻感性负载的三相不控整流桥,其电阻取10Ω ,电感取0.1mH。线路等效电阻为0.05 Ω, Kp=10,K1=600。按照以上模块进行仿真,可得谐波源的电流波形如图7所示。

图7 谐波电流波形及THD
同时,负载电流、指令电流、实际补偿电流的电流波形如图8所示。

图8 负载电流、指令电流和实际补偿电流
由图8可以看出,补偿电流在第一个周期后逐渐跟上指令电流的变化,体现了不错的动态特性。此外,经过补偿后得到的电网电流波形由图9所示。
由图9可以看出,采用PI控制时,系统电网侧电流的TH由30.78%下降为12.94%,系统的性能得到了很大的改善,但是电流波形上仍然存在尖脉冲。
由以上仿真数据可知,PI控制器对直流给定信号可实现无静差的跟踪,但由于APF所控制的谐波信号是交流的,且仍有频率次数不同的交流分量在d-q轴上叠加,此时,PI控制根本无法进行无静差跟踪,不能达到理想的补偿效果。因此,需要考虑采用更好的控制算法来改进APF的性能。

图9 补偿后电网电流波形及THD
2 重复控制器的设计与仿真
近几年来,人们对重复控制策略的研究越来越多,由于非线性负载产生的干扰信号往往是高频且带有周期性的,因而产生的波形失真也具有重复性。故为了消除这些干扰,可考虑采用重复控制的方法。
2.1 重复控制器的基本结构
随着重复控制技术的发展,其控制器的结构也逐渐趋于成熟,图10中虚线标记部分即为其系统框图。

图10 重复控制器系统结构框图
图中,Z-N表示延时一个周期所造成不同周期的误差信号对应的误差点的叠加;Q(z)表示维持系统稳定的系数;S(z)为系统补偿函数部分;Zk用于控制系统的超前或滞后,增强控制器的性能; Kr为重复控制器的增益,可影响系统的稳定性和控制器精度。
2.2 重复控制器的设计与仿真
针对上节所述基本结构,本文设定以下相关参数进行仿真:系统采样频率取6.4kHz,故N=6.4k/50=128;Q(z)=0.95, Kr=0~1.95,另设校正环节如式(8)所示。

根据以上参数构建的重复控制器模型如图11所示。

图11 重复控制器仿真图
将该控制器接入先前所建的数控模型中,得到的仿真图如图12所示。
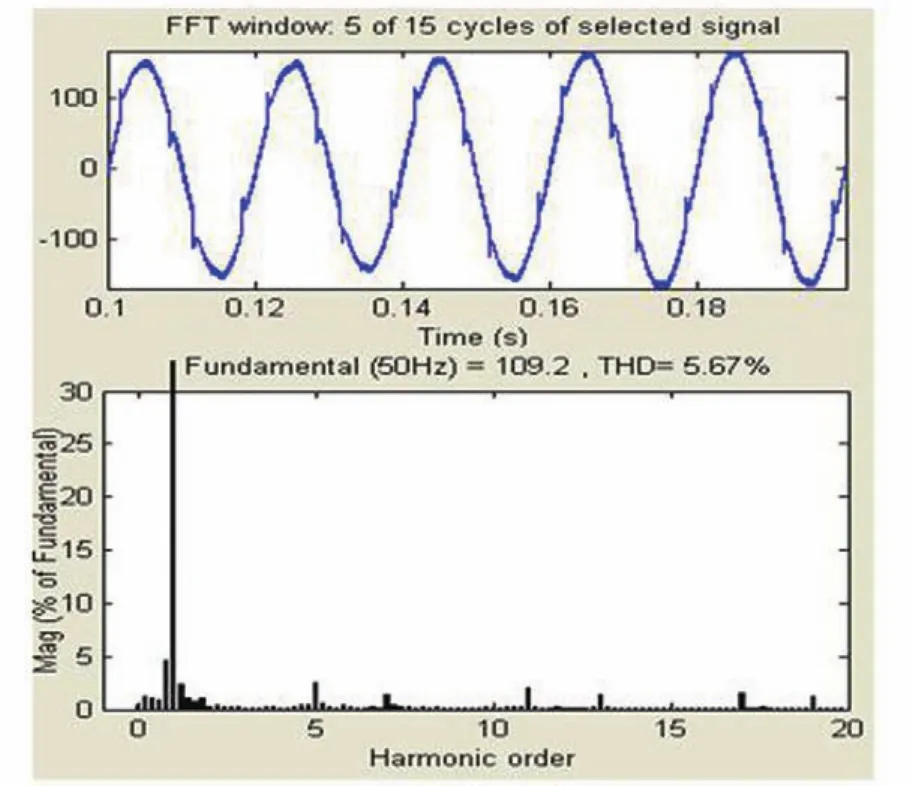
图12 重复控制时电网电流波形
由图12可知,采用该策略后,电网侧电流的THD下降更为明显,同时,前文使用PI调节产生的尖脉冲波也得到了改善。
然而,在直流侧电压方面,对比图13和图14却发现,采用重复控制直流侧电压升至稳定值与较PI控制相比需要更长的时间,且在一个基波周期之后才会调节跟踪误差信号。因此,仅采用重复控制并不能达到理想的效果,需进一步优化。

图13 PI控制时直流电压波形

图14 重复控制时直流侧电压波形
3 基于PI控制和重复控制的复合控制
由前述可知,重复控制的实现是基于基波周期的,具有较好的静态特性,但无法快速响应系统的动态变化;而PI控制的实现则不同,它是基于载波周期的。因此,将二者复合使用,既可通过重复控制来改善补偿精度,又可利用PI控制加快响应速度。而复合的方式有嵌入式和并联式两种形式[20],本文采用将二者并联的方式进行复合控制,其控制结构如图15所示。

图15 并联PI+重复系统控制结构图
按照以上结构,将两种控制器并联使用,取重复控制器的增益Kr为0.7,可以得到补偿后电网侧电流及总体仿真图像如图15和图16所示。由图17仿真结果可知,相对于单纯采用PI控制器而言,电网侧电流的THD大大降低,波形更细,使尖波脉冲得到了有效的改善,正弦度大大提高;同时相较于单纯采用重复控制,其直流侧电压调整的稳定性较好,系统的响应速度较快。综上所述,系统既具有较好的动态特性,又具有不错的静态误差跟踪能力,最终能达到比较好的补偿效果。

图16 并联控制电网电流波形

图17 并联控制的谐波电流、补偿电流、直流侧电压波形图
4 结束语
本文从PI控制和重复控制的原理和结构出发,通过仿真分析了两者分别单独控制时的优点和缺陷,进而采用并联的方式实现复合控制。经过仿真验证,该方案不仅具有较好的动态特性,还大大提高了系统的静态误差跟踪能力,得到的谐波补偿效果较为理想。这表明了该方案在理论上具有可行性,也为更深一步的研究及实际应用提供了参考和依据。
[1] 朱明星,夏振武,管慎龙,等. 并联型有源电力滤波器适用性模型的研究与应用[J]. 电器与能效管理技术, 2014(13):64-69.
[2] 李国华,张影,孙强,等. 有源电力滤波器选择性谐波补偿方法[J电力系统及其自动化学报,2015,27(6):32-36.
[3] 綦慧,赵聪. 有源电力滤波器关键技术的研究[J]. 电气传动自动化,2016, 38(2):1-5.
[4] 张国荣,刘鸷,赵广磊,等. 重复控制下的无变压器混合并联有源电力滤波器[J]. 电器与能效管理技术,2012(16):53-57.
[5] 陈国柱,吕征宇. 有源电力滤波器的一般原理及应用[J]. 中国电机工程学报,2000,20(9):17-21.
[6] 姜齐荣,赵东元,陈建业. 有源电力滤波器:结构·原理·控制[M北京:科学出版社,2005.
[7] 时丽君,赵建国. 有源电力滤波器在电能质量控制中的应用[J]. 电力系统及其自动化学报,2002,14(1):67-71.
[8] 王兆安. 谐波抑制和无功功率补偿[M]. 3版. 北京:机械工业出版社,2016.
[9] 肖湘宁. 电能质量分析与控制 [M]. 北京:中国电力出版社,2010.
[10] 成剑. 基于DSP的有源滤波器谐波检测及其控制方法的研究[D]. 长沙:中南大学,2005.
[11] 陈仲.并联有源电力滤波器实用关键技术的研究[D].杭州:浙江大学,2005.
[12] Akagi H.New trends in active filters for power conditioning[J]. IEE Transactions on Industry Applications,1996,32(6):1312-1322.
[13] 耿攀,戴珂,魏学良,等. 三相并联型有源电力滤波器电流重复控制[J]. 电工技术学报,2007(2):127-131.
[14] 冯宇丽. 数字控制三相三线并联型有源电力滤波器的设计与实现[D]. 武汉:华中科技大学,2007.
[15] 邵伟恒,邹伟,吴上泉. 一种无电压传感器的改进型三相APF控制方法[J]. 电气自动化,2016,38(3):67-70.
[16] 金园园,王正仕,陈辉明,等. 基于根轨迹的单相逆变器PID控制器设计[J]. 机电工程,2008(2):83-85.
[17] Wang R, Pi Y. Fractional-order PI speed control for permanent magne synchronous motor[C]//International Conference on Mechatronics an Automation. IEEE,2012:2303-2308.
[18] Hägglund T,Aring;Sträm K J. Revisiting The ZiegleräNicho Tuning Rules For Pi Control[J]. Asian Journal of Control,2010,6(4):469-482.
[19] Perez M, Ortega R, Espinoza J R. Passivity-based PI control o switched power converters[J]. Control Systems Technology IEEE Transaction on, 2004, 12(6):881-890.
国家自然科学基金(51777025,51477024,51337001), 中央高校基本科研业务专向基金(DUT15ZD234), 强电磁工程与新技术国家重点实验室(华中科技大学)开放课题基金资助(2016KF005)。
