NewtonRaphson算法Logistic分类器性能提升应用研究

叶晓波+秦海菲

摘要：Logistic分类算法中，通常使用梯度上升算法求解权值矩阵，NewtonRaphson算法是另一种求解权值矩阵的算法。选用UCI机器学习仓库中3个数据集，实验研究了Logistic梯度上升算法与Logistic NewtonRaphson算法的分类正确率、权值矩阵迭代求解次数。实验结果表明，相比Logistic梯度上升算法，Logistic NewtonRaphson算法具有更高分类正确率与较少权值矩阵迭代求解次数，该结论为Logistic分类过程中权值矩阵求解算法提供了参考依据。

关键词关键词：模式识别；Logistic；NewtonRaphson

DOIDOI：10.11907/rjdk.171823

中图分类号：TP319

文献标识码：A文章编号文章编号：16727800（2017）011014103

0引言

模式识别是一门以应用为基础的学科，目的是将对象进行分类[1]。根据分类算法训练学习与测试数据集类别标签情况，模式识别可分为有监督模式识别、无监督模式识别及半监督模式识别[1]。监督学习算法中，Logistic分类算法是广泛使用的简单二分类算法，相对于感知器算法，Logistic函数对于输入的任意值，值域为（0，1），完全满足分类算法中概率为（0，1）的要求，且Logistic函数为单调上升函数，没有不连续点。Logistic分类算法中，大部分文献给出求解权值矩阵算法是梯度上升算法，鲜见提及NewtonRaphson算法。这两种算法，哪种具有更快收敛速度与更高分类准确性，本文通过实验研究给出了答案。

3实验研究

实验软件环境为Windows 7（64bit）、Matlab 2016b，硬件环境为Intel I53570K 、8G内存。实验程序设计均在Matlab 2016b下完成，以下是整个实验过程。

3.1数据详情

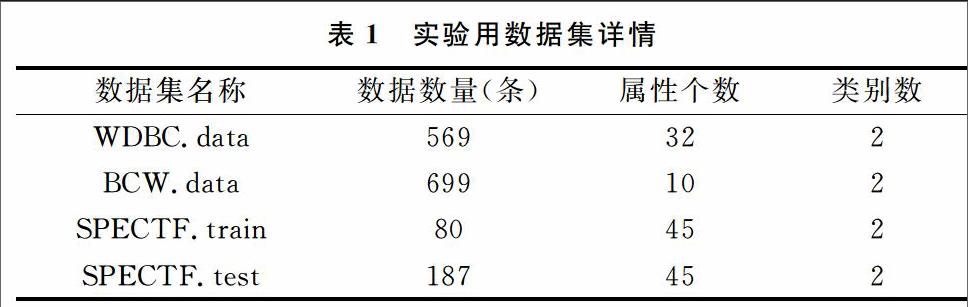
实验所用数据来自UCI机器学习仓库（http：//archive.ics.uci.edu/ml/）较流行的3个数据集，分别为Breast Cancer Wisconsin （Diagnostic）数据集中Wisconsin Diagnostic Breast Cancer （WDBC.data）数据集[8]与Breast Cancer Wisconsin（BCW.data）数据集[9]、SPECT Heart（Data on cardiac Single Proton Emission Computed Tomography images）数据集中SPECTF.train（用于训练学习）与SPECTF.test（用于正确率检测）数据集[10]。实验用数据集数据数量、属性、类别数如表1所示。

所有数据集类别标签分别用数字1、2表示，有缺失值

的数据不参与本次实验，数据预处理情况如下：

WDBC.data数据集第一列属性值为ID number，實验之前应删除该值；第二列属性值为相应类别标签，分别为M、B，实验之前应将数据集中相应类别标识用数字1、2替换。

BCW.data数据集第一列属性值是ID number，实验前应删除该值；最后一列为类别标签，分别为2、4，实验前应将数据集中相应类别标识用数字1、2替换。实验前删除数据集中16条有缺失值的数据。

实验采用UCI数据集的优势在于：UCI数据仓库创建于1987年，是全世界从事机器学习理论研究的学生、教育者、研究人员主要数据源，用UCI数据集得到的实验结果具有一定权威性。

3.2实验思路与方法

3.2.1实验数据采样方法

分类算法分类正确率与实验数据采样比例密切相关，通常训练数据量越大，分类精确度越高。实验中WDBC.data数据集与BCW.data数据集取出每个类别总数量70%数据作为训练学习数据集，余下30%数据作为分类正确率检测数据集；SPECT Heart数据集中的SPECTF.train用于训练学习，SPECTF.test用于分类正确率检测。

3.2.2分类效率比较方式

分别用Logistic梯度上升算法与Logistic NewtonRaphson算法对实验数据进行分类正确率检测，在达到指定分类正确率基础上，对比两种算法的训练学习数据与测试数据分类正确率及迭代求解权值矩阵次数。训练学习数据与测试数据分类正确率高，迭代求解权值矩阵次数少的就是最优算法。

3.3程序设计

3.3.1Logistic梯度上升算法程序设计步骤

（1）load数据集名称；

（2）p=0.7；%提取训练学习数据比例

（3）i=1；%计数器

（4）按比例p提取训练学习数据X；

（5）按比例1-p提取测试数据TX；

（6）w=zeros（size（X，2），1）；%初始化权值矩阵w

（7）按照式（3）计算出梯度上升改变权值矩阵；

（8）EXT=1./（1+exp（-w′*X′））；%代入式（1）计算分类值

（9）X_cor（i） =sum（XT==（EXT>=0.5））/size（XT，2）；%计算分类正确率

（10）while （X_cor（i）<0.9）%迭代求解的条件是分类正确率小于90%

（11）i=i+1；%迭代次数计数

（12）按照式（10）计算出梯度上升改变权值矩阵；

（13）EXT=1./（1+exp（-w'*X'））；%代入式（1）计算分类值

（14）X_cor（i）=sum（XT==（EXT>=0.5））/size（XT，2）；%计算分类正确率endprint

（15）end

3.3.2Logistic NewtonRaphson算法程序设计步骤

（1）load数据集名称；

（2）p=0.7； %提取训练学习数据比例

（3）i=1；%计数器

（4）按比例p读取训练学习数据X；

（5）按比例1-p读取测试数据TX；

（6）w=zeros（size（X，2），1）； %初始化权值矩阵w

（7）按照式（4）计算出梯度上升改变权值矩阵；

（8）EXT=1./（1+exp（-w′*X′））；%代入式（1）计算分类值

（9）X_cor（i） =sum（XT==（EXT>=0.5））/size（XT，2）；%计算分类正确率

（10）while （X_cor（i）<0.9）%迭代求解的条件是分类正确率小于90%

（11）i=i+1；%迭代次数计数

（12）按照式（13）计算出梯度上升改变权值矩阵；

（13）EXT=1./（1+exp（-w′*X′））；%代入式（1）计算分类值

（14）X_cor（i）=sum（XT==（EXT>=0.5））/size（XT，2）；%计算分类正确率

（15）end

3.4实验结果分析

实验结果见表2、表3。

分析表2、表3可知，Logistic NewtonRaphson算法训练数据与测试数据分类正确率都高于Logistic梯度上升算法；在迭代求解次数方面Logistic NewtonRaphson算法仅需2次迭代就求出符合要求的权值矩阵，明显少于Logistic梯度上升算法，说明Logistic NewtonRaphson算法在分类正确率与迭代求解次数两方面都优于Logistic梯度上升算法。

提高测试数据分类正确率，如要求测试数据分类正确率高达96%（可能会出现过拟合现象），Logistic梯度上升算法无法收敛，而Logistic NewtonRaphson算法却能快速收敛，这充分说明两种算法存在效率差别。

4结语

本文从分类正确率、权值矩阵迭代求解次数两方面对Logistic梯度上升算法与Logistic NewtonRaphson算法进行了研究。实验用数据源自权威UCI机器学习仓库，实验数据除SPECTF数据集已经分配好训练数据与测试数据集外，另外两个数据集（WDBC.data与BCW.data）均选取每个类别70%数据作为训练学习数据，余下30%数据作为模型测试数据。实验结果如下：①Logistic NewtonRaphson算法训练数据与测试数据分类正确率均高于Logistic梯度上升算法；②LogisticNewtonRaphson算法僅2步迭代就求解出权值矩阵，而Logistic梯度上升算法需要更多迭代次数才能求解。以上说明，相比Logistic梯度上升算法，Logistic NewtonRaphson算法分类准确率高、运行效率优越。

参考文献参考文献：

[1]SERGIOSTHEODORIDIS， KONSTANTINOS KOUTROUMBAS.模式识别 [M].李晶皎，王爱侠，王骄，等，译.北京：电子工业出版社，2011.

[2]王德辉，杨帆，杨凯.具有LOGISTIC回归结构的几何分布参数贝叶斯估计及应用[J].辽宁师范大学学报：自然科学版， 2016 （3） ：1316.

[3]万会芳，杜彦璞.K近邻和LOGISTIC回归分类算法比较研究[J].洛阳理工学院学报：自然科学版，2016（3）：8386.

[4]百度百科.牛顿迭代法[EB/OL].https：//baike.baidu.com/item/%E7%89%9B%E9%A1%BF%E8%BF%AD%E4%BB%A3%E6%B3%95/10887580.

[5]云磊.牛顿迭代法的MATLAB实现[J].信息通信，2011（6）：26.

[6]ANDREW NG.Lecture notes 1[EB/OL].http：//cs229.stanford.edu/materials.html.

[7]ANDREW NG.Homework 1： solutions[EB/OL].http：//cs229.stanford.edu/materials.html.

[8]O L MANGASARIAN，W N STREET，W H WOLBERG.Breast cancer diagnosis and prognosis via linear programming [J].Operations Research，1995， 43（4）：570577.

[9]O L MANGASARIAN，W H WOLBERG.Cancer diagnosis via linear programming [J].SIAM News，1990（23）：118.

[10]LA KURGAN， KJ CIOS， R TADEUSIEWICZ， et al. Knowledge discovery approach to automated cardiac SPECT diagnosis[J].Artificial Intelligence in Medicine， 2001，23（2）： 149169.

责任编辑（责任编辑：何丽）endprint