视情维修条件下的多状态控制单元可用性建模与分析
2017-12-01李志强徐廷学顾钧元安进董琪
李志强, 徐廷学, 顾钧元, 安进, 董琪
(海军航空大学 兵器科学与技术系, 山东 烟台 264001)
视情维修条件下的多状态控制单元可用性建模与分析
李志强, 徐廷学, 顾钧元, 安进, 董琪
(海军航空大学 兵器科学与技术系, 山东 烟台 264001)
针对传统可靠性分析方法难以描述系统动态特性的问题,提出了一种基于多状态动态贝叶斯网络的视情维修可用性建模方法。在定义多状态元件的基础上,构建了基于Markov模型的视情维修状态转移模型,并引入了吸收状态。通过构建多状态动态贝叶斯网络模型,确定了无维修、完全维修、不完全维修、视情维修和吸收状态下的状态转移关系,并根据串联和并联逻辑关系对条件概率赋值。以某控制单元为例,构建动态故障树模型、动态贝叶斯网络模型,确定控制单元与元件在不同维修方式下的可用度变化规律,通过重要度分析发现了可靠性设计中的薄弱环节。仿真分析表明:视情维修的引入使得控制单元与元件相对于完全维修与不完全维修具有更高的可用度;吸收状态的引入可以预测退化状态可修元件的可用度变化趋势,为维修换件提供理论指导。
兵器科学与技术; 动态贝叶斯网络; 视情维修; 完全维修; 不完全维修; 动态故障树; 重要度分析
0 引言
传统的可靠性分析方法如故障树分析、二元决策图、故障模式影响分析等假设系统具有正常运行与故障失效二种状态。随着系统朝着复杂化、结构化等方向发展,冗余设计、优先门等逻辑事件的引入,传统可靠性分析方法的局限性逐渐凸显出来。Langseth等[1]提出了故障树逻辑门向贝叶斯网络节点转化的方法,并研究了贝叶斯网络在系统可靠性分析中的应用。贝叶斯网络具有正向推理、反向推理、不确定关系表达等优势[2-4],并克服了传统可靠性分析方法独立性假设和二元状态假设的缺陷。复杂系统的状态随着时间与运行条件发生改变,静态可靠性分析方法主要用于初始时刻或者某一特定时刻的性能指标评估,难以描述性能特征参数的动态变化规律。在静态贝叶斯网络和隐Markov模型基础上发展起来的动态贝叶斯网络,避免了Markov建模的组合爆炸问题,也避免了动态故障树求取最小割集的繁琐程序[5-7]。周忠宝等[8-9]研究了动态故障树向动态贝叶斯网络的转化方法,并应用于工程实践中。
可用性[10],即在规定的条件下,装备在任意时刻t能够正常工作的概率。可靠性和可用性的定义极为相似,实际上,可用性是可靠性、维修性和保障性的综合反映。由于可用性同时考虑了元件的劣化过程和维修过程,Markov过程充分考虑了元件各状态之间的转移关系,刘航等[11]从维修时间和费用的角度出发,提出了基于Markov模型的组合式维修决策建模与优化方法;耿岩等[12]在考虑休眠因子的情况下,构建了基于Markov模型的两部件系统可用度分析模型,预测备件需求与系统可用度。鉴于Markov模型存在组合爆炸、难以描述复杂系统可用度的问题,王少华等[13]从维修费用的角度出发,针对多部件系统随机劣化过程建立了基于蒙特卡洛仿真的决策优化模型。蒙特卡洛仿真有效地解决了可用性分析中的数据缺乏问题,但是,对于具有成百上千部件的复杂系统,对部件难以逐一仿真。因此,樊冬明等[14]研究了基于动态贝叶斯网络的GO法模型算法,Liu等[15]、Cai等[16]利用动态贝叶斯网络分析了海底封井器的共因失效与考虑不完全维修的可用性问题。
针对人难以介入的装备,以事后维修为主,当故障事件发生后采取完全维修或者不完全维修;对于时常处于监测条件下的装备,可以从某一退化状态开始采取视情维修(CBM)。本文在应用Markov过程进行系统状态关系转移建模的基础上,构建动态贝叶斯网络可用性分析模型,针对完全维修、非完全维修和CBM进行动态分析,并考虑具有吸收状态的可用性模型。
1 基于Markov过程的多状态元件状态转移模型
CBM立足于故障机理分析,根据不解体测试结果对出现“潜在故障”的装备进行维修或者更换,从而避免“功能故障”的发生。CBM的优势在于通过监测手段,掌握装备的实时技术状态,及时发现问题并采取相应的维修措施,从而避免严重故障的发生,进而有效地降低装备的故障发生率,节约维修成本,减少维修工作量,解决定期维修过程中存在的维修不足与维修过剩问题。
1.1 多状态元件定义
多状态元件相对于传统可靠性分析方法中的二状态元件而言,元件除了正常运行与故障失效,具有介于正常运行与故障失效之间的中间退化状态。根据划分标准的不同,中间状态可以是一个状态,也可以是多个状态。现假设某元件具有k个不同的技术状态,由g={g1,g2,…,gk}表示(gk表示元件的初始状态,g1表示元件的失效状态,gi表示元件处于初始状态与失效状态之间的劣化状态),对于任意的i,gi+1≥gi. 对于可修元件,一旦发生故障立即安排技术人员进行修理,其寿命周期由运行时间和维修时间组成。一个元件的可接受状态取决于元件当前的性能状态与满足工作需求必需的性能水平。令元件的状态函数为G(t)∈g,性能水平函数为W(t),W(t)∈w={w1,w2,…,wm}(wi为不同的性能水平),对于处于可接受状态的元件,有:G(t)≥W(t).
1.2 多状态元件CBM模型
多状态元件的失效模式可以分为渐变劣化和突变劣化,相应的维修方式可以分为最小维修、非完好维修和换件维修,构建如图1所示的状态空间转移模型。令失效率由λ表示,维修率由μ表示。假设起始时刻元件处于最佳状态k,随时间可能发生转移到状态k-1的渐变劣化,也可能发生转移到状态i(i

图1 元件劣化与维修的状态转移模型Fig.1 State transition diagram of failed and repaired components
根据元件Markov状态转移模型[17-18],建立如下的微分方程组:
(1)
式中:λi,j为元件从状态i转移到状态j的劣化密度函数;μj,i为元件从状态j转移到状态i的维修密度函数;pi(t)为元件处于状态i的概率函数。
在初始时刻:
pk(0)=1,pk-1(0)=pk-2(0)=…=p1(0)=0.
(2)

(3)
1.3 考虑吸收状态的维修模型
为了确定指定性能水平w(gi
(4)
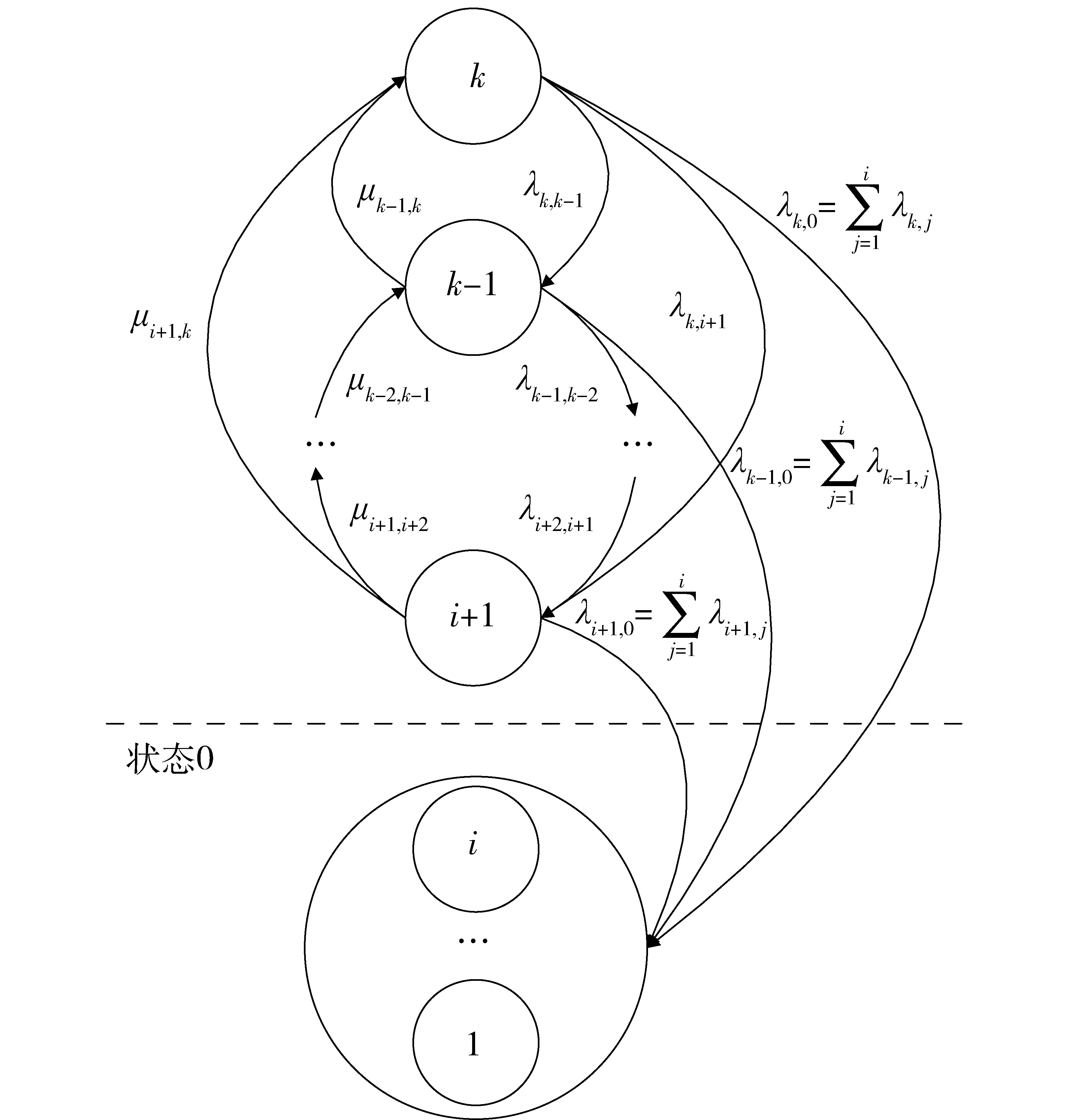
图2 指定水平下元件状态转移图Fig.2 State-transition diagram of component under certain demand rate
构建元件状态转移的可靠度函数为
(5)
初始条件与(2)式相同,则元件的可用度函数为
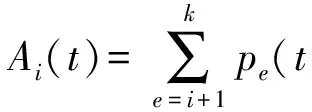
(6)
当元件所处技术状态高于指定性能水平w时,元件为可用状态,其可用度函数可以通过元件所处各个可用状态的概率函数表征。以图2为例,元件可用的技术状态为i+1,i+2,…,k,对应的状态概率函数为pi+1(t),pi+2(t),…,pk(t),则元件此时的可用度函数为所处各可用技术状态的概率之和,即如(6)式所示。
当t→∞时,元件将进入吸收状态0,系统最终状态概率为
pk=pk-1=…=pi+1=0,p0=1.
(7)
2 基于动态贝叶斯网络的状态转移模型
2.1 动态贝叶斯网络概述
动态贝叶斯网络表示为(B1,B→),B1为初始贝叶斯网络,B→为包含时间片的贝叶斯网络。相邻两个时间片各变量之间的条件分布[6, 19]表示为
(8)
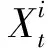
假设各节点之间的有向边位于同一个时间片内,或者位于相邻的时间片上,动态贝叶斯网络的结构参数不随时间发生变化,即跨越多个时间片的概率分布[20]表示为
(9)
式中:X1:T={X1,X2,…,XT}.
2.2 动态贝叶斯网络多状态建模
故障树的串联结构、并联结构可以直接转换为贝叶斯网络模型,在图3中,图3(a)为串联结构动态贝叶斯网络(DBN)模型,图3(b)为并联结构DBN模型。故障树的每个基本事件转化为贝叶斯网络(BN)模型中对应的父节点,顶事件转化为子节点。引入时间序列,静态BN模型拓展成了DBN模型,同一时间片内变量之间的逻辑关系用实线箭头表示,连续时间片上变量之间的逻辑关系用虚线箭头表示。
在图3串联系统和并联系统中,节点A和节点B通过时间片间的箭头从时间t=1拓展到t=2. 由于节点A与节点B之间无箭头,彼此之间无逻辑关系。节点A和节点B具有4个状态,即良好(Perfect,P)、堪用(Useful,U)、拟故障(Psendo-fault,P-F)和故障(Fault,F),子节点C具有两个状态,即正常(Normal)和故障(Fault)。状态良好、正常表示系统无失效或者正常运行,故障表示系统处于完全失效状态,堪用和拟故障分别表示1级退化状态和2级退化状态。假设父节点A和父节点B的失效率分别为λA=3×10-3,λB=2×10-3,维修率分别为μA=5×10-2,μB=8×10-2. 除了有不同的条件概率表,并联系统与串联系统有同样的DBN结构,在给定同样数据的情况下,相比于串联系统,并联系统具有更高的可靠度。
2.3 CBM动态贝叶斯网络建模
对于多状态退化系统,作出如下假设:
1)系统退化具有多个性能等级,在良好运行与故障失效之间取值;
2)系统可能在任一运行状态发生劣化,包括渐变劣化和突变劣化;
3)所有的状态转移概率为常数,服从指数分布;
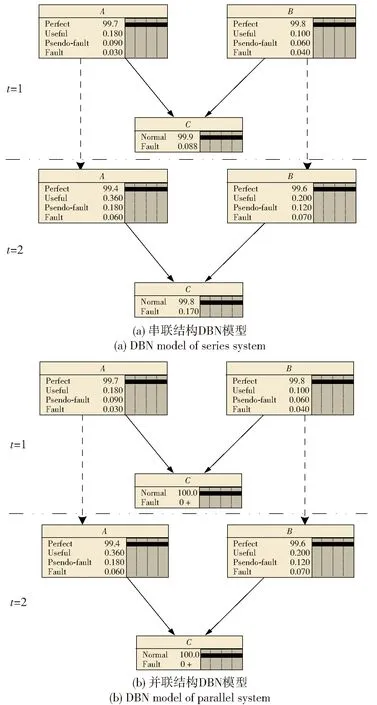
图3 二元件串联和并联DBN模型Fig.3 DBN models of series system and parallel system with two components
4)通过一些参数可以观测系统当前的退化状况,监测时间忽略不计。
假设多状态贝叶斯网络的每个父节点具有良好、堪用、拟故障和故障4个状态[21-22]。每个父节点在初始时刻都是正常运行的。随着时间的推进,系统可能进入堪用状态或者拟故障状态,或者直接进入失效状态。对于人难以介入或者必须停机检查的装备,当故障事件发生之后,采取维修措施使元件节点从故障状态直接进入正常运行状态,即完全维修;也可能从故障状态进入到堪用、拟故障两个退化状态,即不完全维修。对于处于可观测条件下的关键装备,采取CBM方式,即当监测到系统发生系统退化时即可采取维修手段,从当前状态恢复到初始状态或者上一级退化状态。图4为4个状态元件状态转移过程。相比于完全维修与不完全维修,CBM可以从状态2恢复到状态4或者状态3,也可以从状态3恢复到状态4,而不是在元件发生故障失效之后再采取维修措施。

图4 4个状态元件状态转移图Fig.4 State-transition diagram of a four-state component
假设当前为t时刻,两个连续时间片间隔为Δt,则节点在连续时间片间无维修、完全维修、不完全维修和CBM的状态转移关系如表1~表4所示。
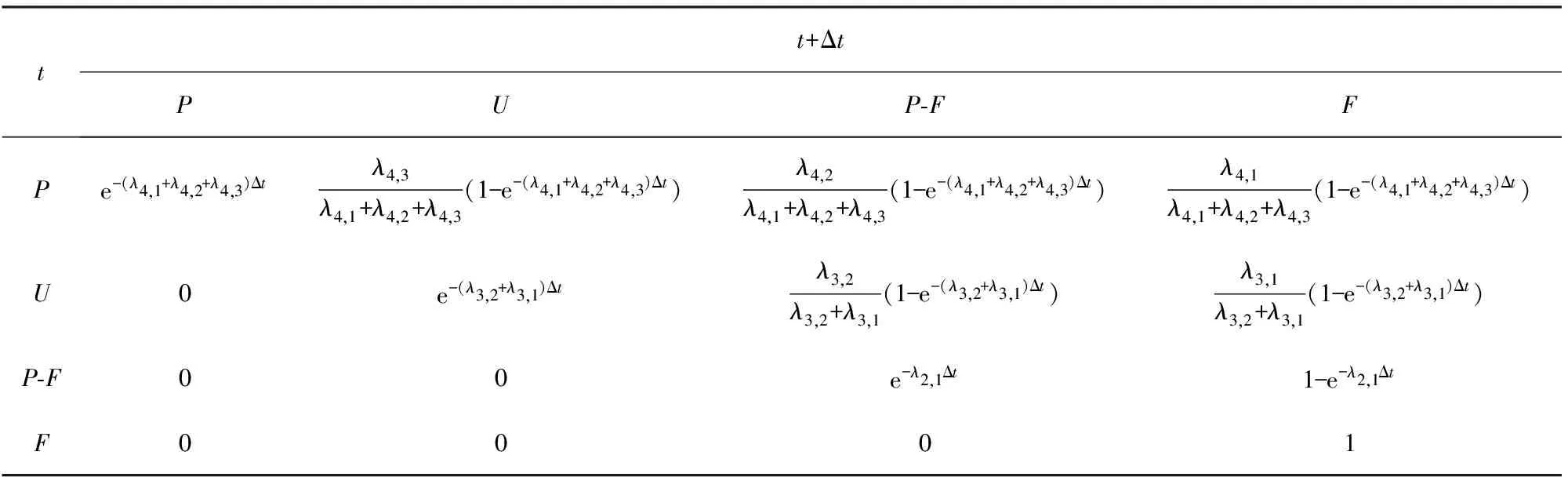
表1 无维修节点状态间转移关系
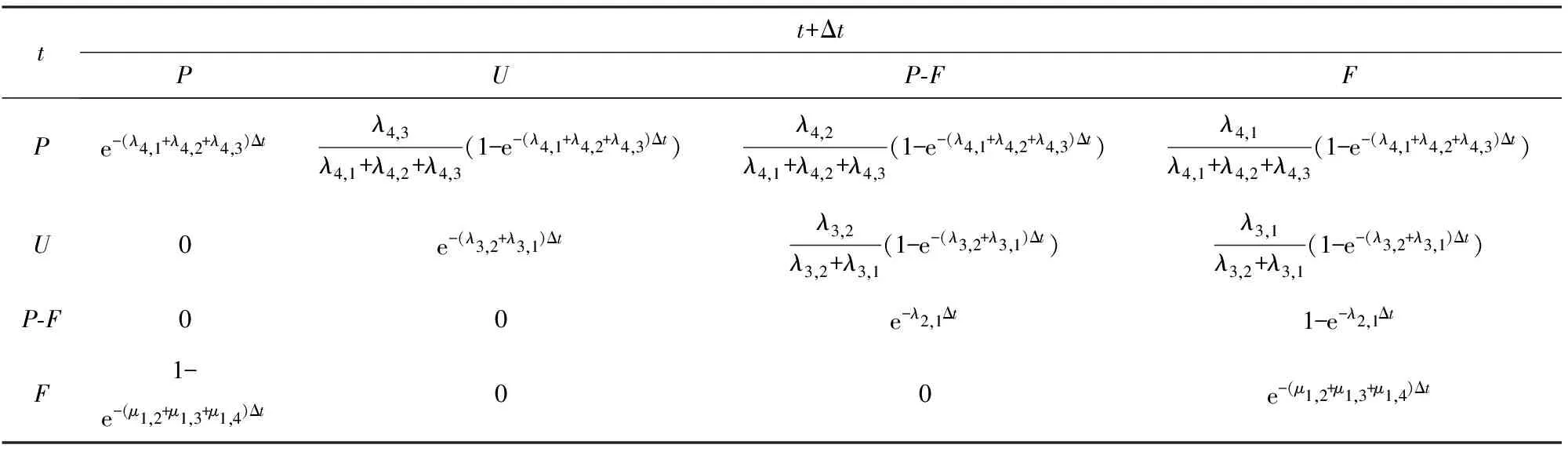
表2 完全维修节点状态间转移关系
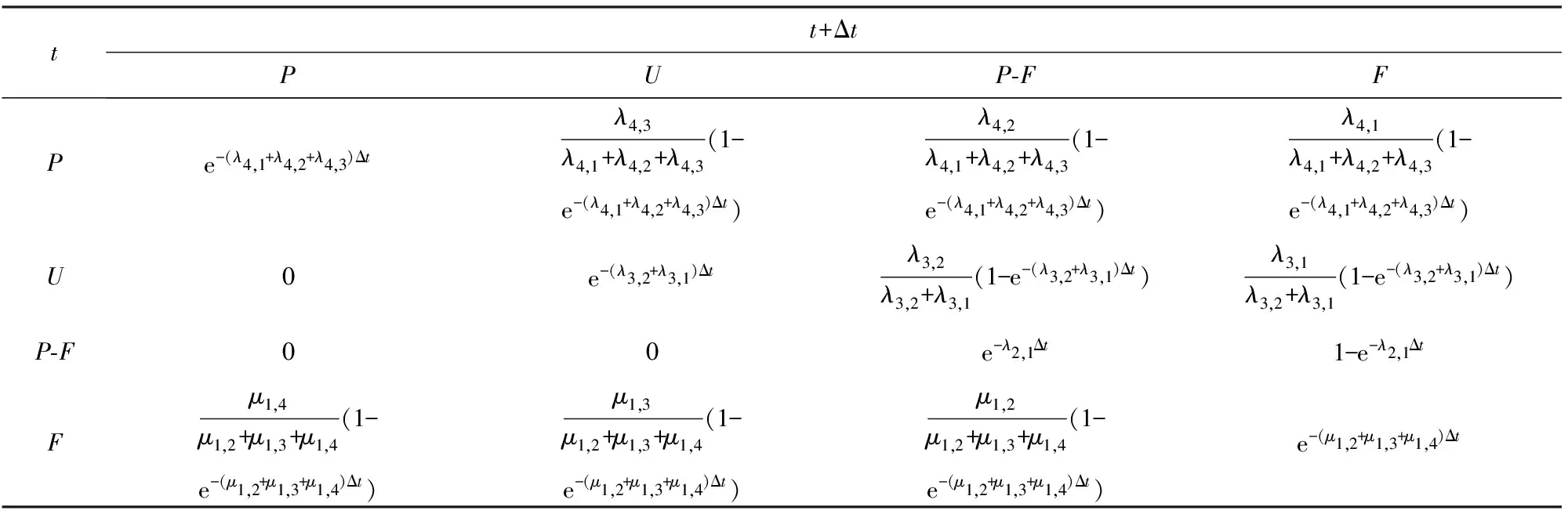
表3 不完全维修节点状态间转移关系

表4 CBM节点状态间转移关系
在CBM方式下,不可忽略的一种特殊维修方式,即具有吸收状态的CBM. 0状态表示一个不可接受的失效状态集,这一状态可以直接设定为报废状态,从这一状态到任一状态的转移都是不允许的。以表4为例,假设F为失效状态集,只考虑从1级退化状态U和2级退化状态P-F向上1级或2级的维修状态转移,而不考虑从失效状态到其余3个状态级的维修状态转移。现假设P-F和F构成失效状态集{P-F,F},则节点状态之间的转移关系可表示为表5.

表5 以{P-F,F}为吸收状态集的节点状态间转移关系
2.4 条件概率赋值
对一个具有n个父节点,每个父节点具有m个状态的DBN模型,需要mn个独立参数确定结构参数条件概率表(CPT)。当父节点较多时,难以对每个参数定量赋值,因此,为了简化条件概率赋值问题,从串联和并联系统结构出发,根据元件各状态条件失效率作定量计算。假设Y具有n个父节点X1,X2,…,Xn,每个父节点条件失效率为fj,对于串联结构,n个元件串联的不可靠度为
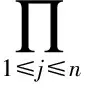
(10)
对于并联系统,不可靠度为
(11)
假设图3中由节点A和节点B构成的串联和并联系统中,条件失效率概率为:P(F=1|UA=1)=4%,P(F=1|P-FA=1)=6%,P(F=1|UB=1)=2%,P(F=1|P-FB=1)=5%,根据(10)式、(11)式即可确定串联和并联系统的CPT.
3 实例分析
3.1 控制单元动态故障树模型构建
某控制单元由多种电子元器件、机械部件构成,结构复杂,故障模式多样,在复杂运行条件下受多种环境应力影响,性能指标随时间逐渐退化。实时的参数监测能够判断出控制单元性能指标合格与否,而预判性的可靠性分析可以为维修决策制定、维修资源优化提供方法指导。现以控制单元电源故障为例建立可靠性分析模型,以控制单元电源故障为顶事件建立如图5所示的动态故障树。顶事件(TE)失效由3个中间事件引起,即模块sys1失效、模块sys2失效和模块sys3失效:模块sys1包含一个静态与门,由元件C1、元件C2组成;模块sys2失效由元件C3元件失效、元件C6失效和模块sys4失效构成;模块sys4失效由热储备门(HSP)元件C4失效、元件C5失效引起;模块sys3包含一个温储备门(WSP),由元件C7和元件C8组成。
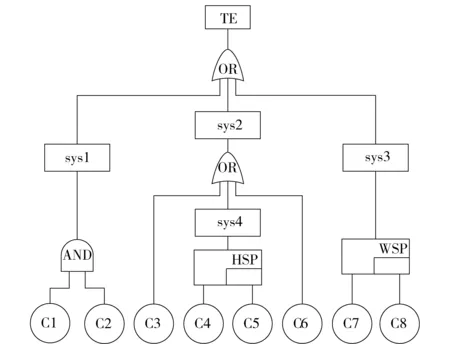
图5 控制单元电源故障动态故障树模型Fig.5 DFT model of control unit with power in failure
3.2 控制单元动态贝叶斯网络模型构建
控制单元中各元件的失效率、维修率和失效条件概率如表6所示,假设元件C8的休眠因子为0.1.

表6 控制单元元件参数
为了简化计算,对多状态元件各状态之间失效率与维修率作如下假设:
λ3,1=λ4,2,λ4,3=λ3,2=λ2,1,λ4,1+λ4,2+λ4,3=λ,λ4,1∶λ4,2∶λ4,3=1∶3∶6;μ1,3=μ2,4,μ1,2=μ2,3=μ3,4,μ1,2+μ1,3+μ1,4=μ,μ1,2∶μ1,3∶μ1,4=2∶3∶5.
根据动态故障树向动态贝叶斯网络转化原理,构建控制单元的动态贝叶斯网络模型,如图6所示。以表6中的数据确定输入值和条件概率值,取动态贝叶斯网络时间片t=1时刻和t=2时刻,建立控制单元在CBM情况下的状态转移模型,如图7所示。在初始时刻,各元件可靠度为100%,经历时间片1和时间片2,各个不同状态具有不同的退化概率值。

图6 控制单元电源故障DBN模型Fig.6 DBN model of control unit with power in failure
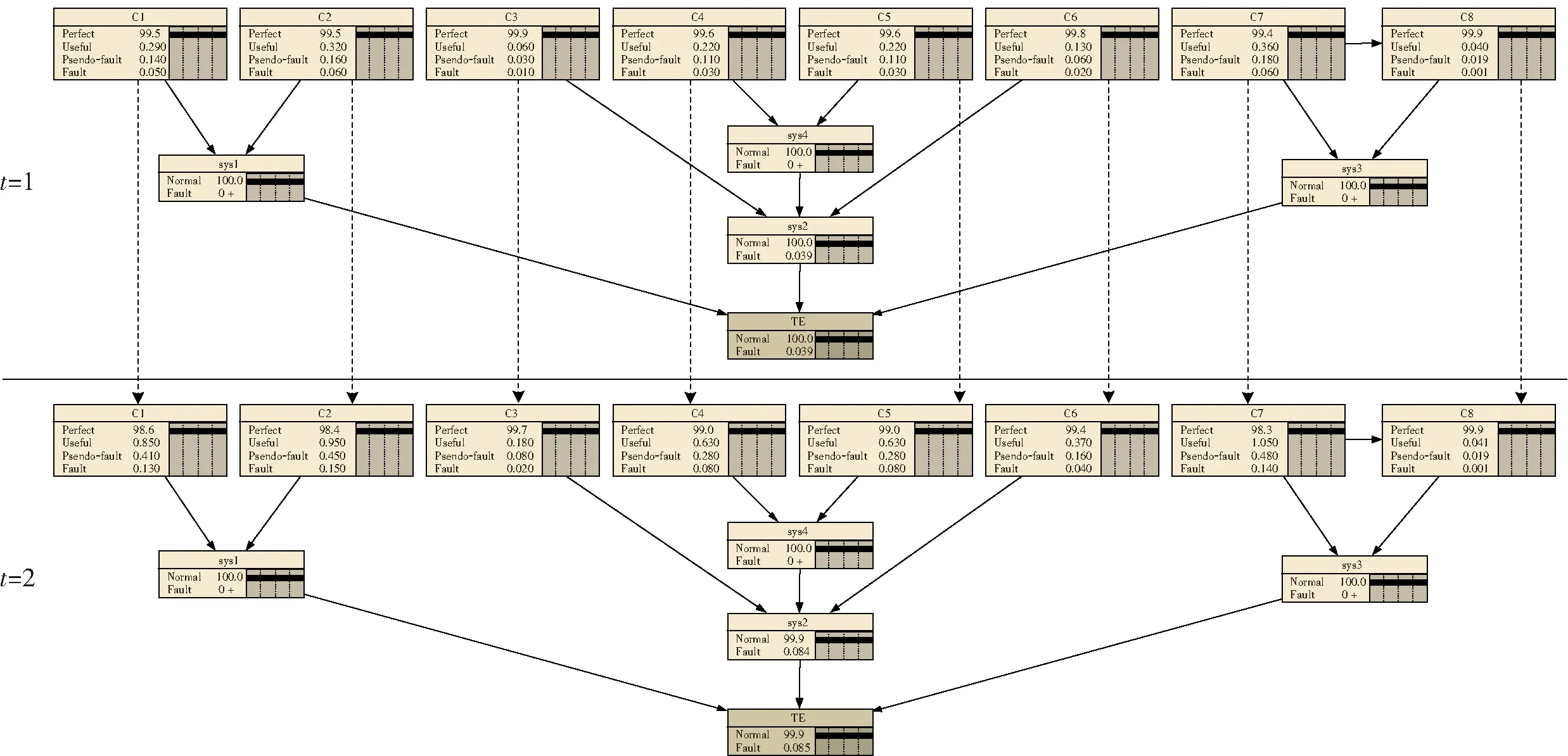
图7 时间片t=1到t=2的DBN模型Fig.7 DBN model of control unit for t=1 and t=2
3.3 模型验证与可靠性分析
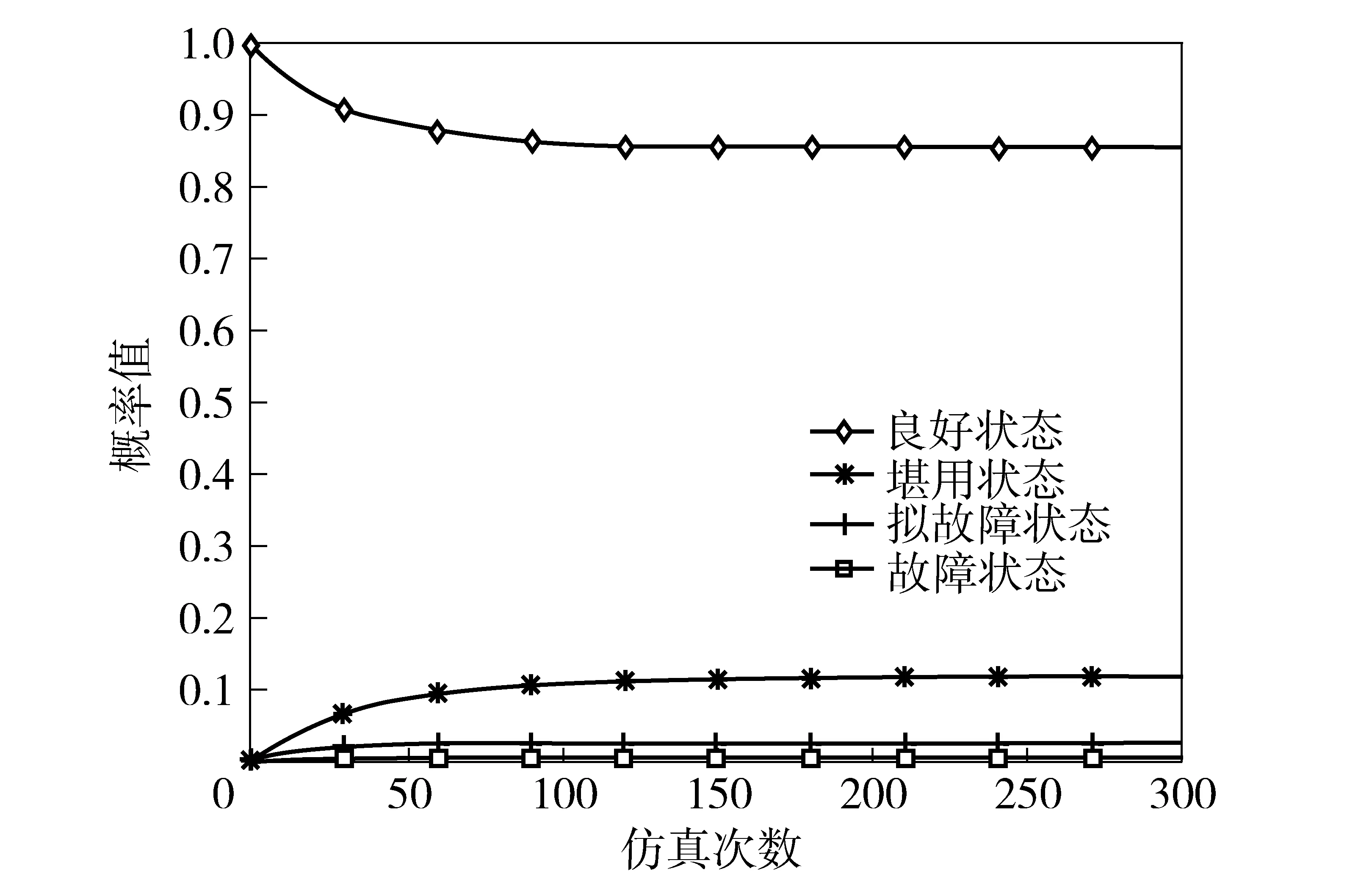
图8 CBM下元件C1处于各状态的概率曲线Fig.8 Probability curves of component C1 in all states under condition-based maintenance
在CBM情况下,当元件发生性能指标退化时,通过监测参数可以判定退化程度,如果元件退化到堪用状态,采取维修措施可以使元件恢复到良好状态;如果元件退化到拟故障状态,采取维修措施可以使元件恢复到良好状态或者堪用状态;如果元件发生了失效,采取维修措施可以使元件恢复到可用状态中的某一状态,而进行换件维修可以使元件处于良好状态。以元件C1为例,参考表6中的失效率、维修率,根据(1)式建立元件各状态转移关系(12)式,求解微分方程,确定元件隶属于各个状态的概率曲线,如图8所示。利用构建的动态贝叶斯网络模型获得了同样的仿真结果,这正好验证了模型构建的准确性。在约第130周时,各状态的概率值趋于平稳,以元件处于良好状态概率最高。
(12)
建立控制单元在完全维修、非完全维修和CBM情况下的可用度曲线,如图9所示。仿真1 000次,3种维修方式都具有很高的可用度,完全维修高于0.95,由于CBM可以对处于退化状态中的元件采取维修措施,具有最高的可用度,符合实际情况。
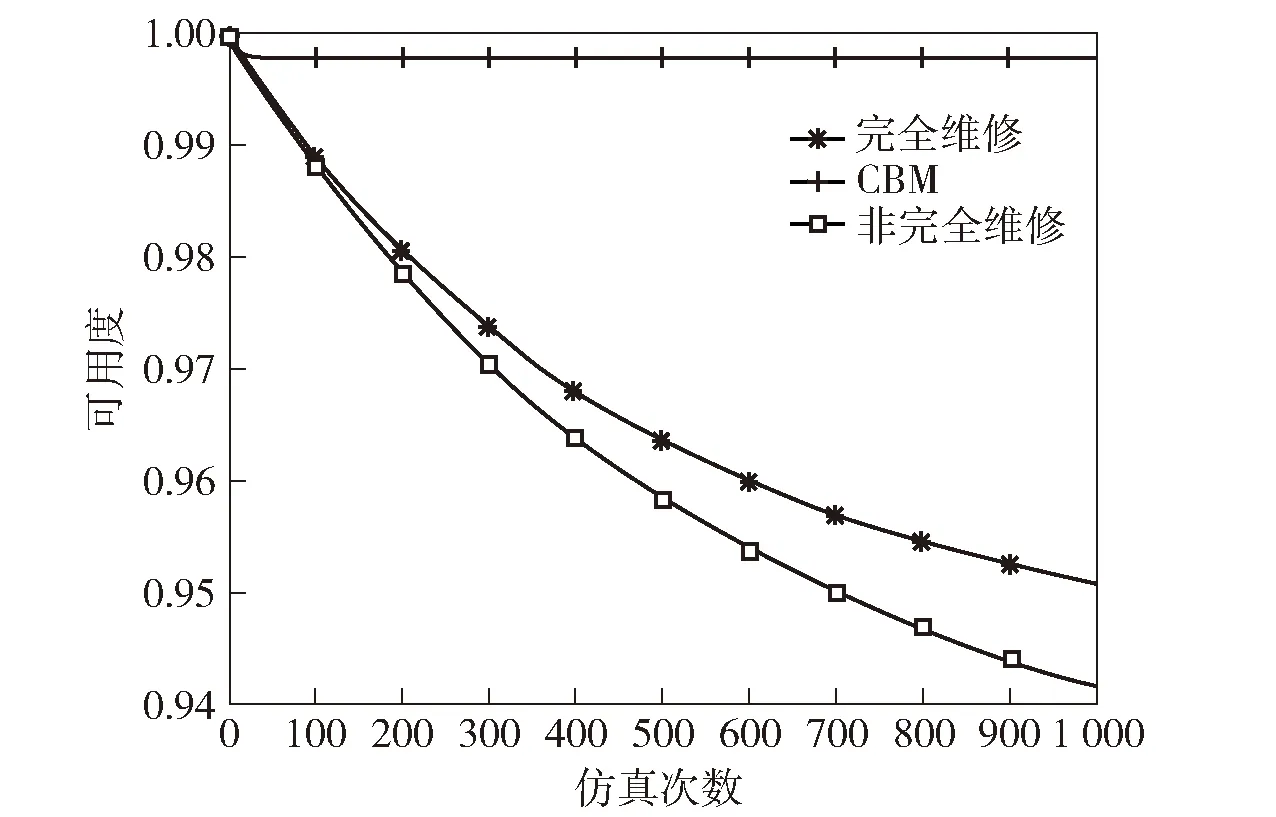
图9 控制单元完全维修、非完全维修和CBM可用度曲线Fig.9 Availability curves of control unit under perfect repair, imperfect repair and condition-based maintenance
对于某些可靠性要求高的元件,当参数指标低于一定阈值就不再满足使用要求,并且无法通过维修使故障件回到可使用状态,即作报废处理。以元件C1为例,假设只有处于良好状态、堪用状态的元件满足使用需求,拟故障状态、故障状态判为报废处理状态。根据(5)式建立状态转移关系(13)式,确定元件处于各状态的概率曲线,如图10所示。由于良好状态随时间不断向堪用状态和吸收状态转化,其概率曲线逐渐降低,处于堪用状态的概率值在升高之后也随之逐渐减低,处于吸收状态的概率曲线一直上升,最终将达到1.
(13)

图10 吸收状态{P-F,F}下元件C1各状态概率曲线Fig.10 Probability curves of component C1 in all states under absorbing set {P-F, F}
如图11所示,以控制单元为例,{P-F,F}吸收状态比无维修状态下可用度曲线下降更快更明显。如果以故障状态为吸收状态,可用度曲线下降相对缓和。由于存在中间状态到良好状态的CBM,系统可用度值在第1 000周之后仍然较高。
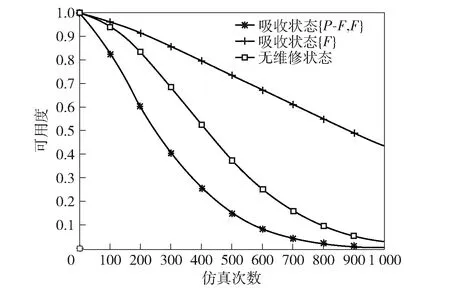
图11 吸收状态与无维修条件下控制单元可用度曲线Fig.11 Availability curves of control unit under absorbing sets and without repair
3.4 元件重要度分析
元件的重要度分析关键在于确定系统中的相对重要度高的元件,发现可靠性设计与分配中的薄弱环节。贝叶斯网络中节点的重要度可分为结构重要度、概率重要度、关键重要度[23-24]:对控制单元进行结构重要度分析可知,节点C3和节点C6为串联节点,具有相对较高的结构重要度。应用BayesiaLab软件进行动态贝叶斯网络仿真分析,节点C3和节点C6为子节点TE提供更多的交互信息,因此具有更高的相对重要度,如图12所示。为确保控制单元具有足够的可用度,以控制单元正常运行为证据进行反向推理,获得各元件节点的可靠度指标,以节点C3和节点C6最高,分别为0.983 8和0.976 9. 因此,在进行控制单元设计时,应尽量选用具有高可靠性的节点C3和节点C6,并对使用中的元件C3和C6合理安排维修周期。

图12 控制单元元件重要度分析Fig.12 Importance analysis of components in control unit
4 结论
针对可以进行CBM的装备,在Markov模型的基础上提出了基于动态贝叶斯网络的可用性分析方法,通过建模与仿真分析,得到如下主要结论:
1)多状态元件Markov模型的构建清晰地表示了元件各状态之间的转移关系,根据微分方程组Laplace-Stieltjes变换理论可以确定元件处于各个状态的概率值。
2)多状态动态贝叶斯网络的构建简化了多元件系统的可用性建模,元件各状态之间的转移关系根据转移密度函数确定。
3)基于CBM的控制单元相对于完全维修与不完全维修具有更高的可用度,为关键、重要件维修决策制定提供了理论指导。
4)吸收状态的引入可以预测退化状态可修元件的可用度,相比于不可修元件,以故障失效为吸收状态的元件具有更高的可用度,CBM方式保证了元件更长的使用寿命。
References)
[1] Langseth H, Portinale L. Bayesian networks in reliability[J]. Reliability Engineering & System Safety, 2007, 92(1):92-108.
[2] Mahadevan S, Zhang R, Smith N. Bayesian networks for system reliability reassessment[J]. Structural Safety, 2001, 23(3):231-251.
[3] Lisnianski A, Frenkel I, Ding Y. Multi-state system reliability analysis and optimization for engineers and industrial managers[M]. New York, NY, US: Springer, 2010: 29-66.
[4] Wilson A G, Huzurbazar A V. Bayesian networks for multilevel system reliability[J]. Reliability Engineering & System Safety, 2007, 92(10):1413-1420.
[5] Codetta-Raiteri D, Bobbio A, Montani S, et al. A dynamic Bayesian network based framework to evaluate cascading effects in a power grid[J]. Engineering Applications of Artificial Intelligence, 2012, 25(4): 683-697.
[6] Barua S, Gao X D, Pasman H, et al. Bayesian network based dynamic operational risk assessment[J]. Journal of Loss Prevention in the Process Industries, 2016, 41:399-410.
[7] Zhang L M, Wu X G, Skibniewski M J, et al. Bayesian-network-based safety risk analysis in construction projects[J]. Reliability Engineering & System Safety, 2014, 131(3):29-39.
[8] 周忠宝,周经伦,孙权,等. 基于离散时间贝叶斯网络的动态故障树分析方法[J]. 西安交通大学学报, 2007, 41(6): 732-736.
ZHOU Zhong-bao, ZHOU Jing-lun, SUN Quan, et al. Dynamic fault tree analysis method based on discrete time Bayesian networks[J]. Journal of Xi’an Jiaotong University, 2007, 41(6): 732-736. (in Chinese)
[9] 周忠宝,马超群,周经伦,等. 基于动态贝叶斯网络的动态故障树分析[J]. 系统工程理论与实践, 2008, 28(2): 35-42.
ZHOU Zhong-bao, MA Chao-qun, ZHOU Jing-lun, et al. Dynamic fault tree analysis based on dynamic Bayesian networks[J]. Systems Engineering—Theory & Practice, 2008, 28(2): 35-42. (in Chinese)
[10] 于春雨,郭建英,苑惠娟,等. 指数故障/维修背景下串联系统可用度置信限[J]. 仪器仪表学报, 2016, 37(5): 1079-1086.
YU Chun-yu, GUO Jian-ying, YUAN Hui-juan, et al. Confidence limit of series system availability in exponential fault time and repair-time context[J]. Chinese Journal of Scientific Instrument, 2016, 37(5): 1079-1086. (in Chinese)
[11] 刘航,李群湛,郭锴. 基于Markov过程的组合式同相供电装置维修决策优化[J]. 西南交通大学学报, 2017, 52(2): 1-8.
LIU Hang, LI Qun-zhan, GUO Kai. Research on combined co-phase power supply equipment maintenance decision modeling and optimization based on Markov process[J]. Journal of Southwest Jiaotong University, 2017, 52(2): 1-8.(in Chinese)
[12] 耿岩,郭霖瀚,王寄明,等. 考虑休眠的两部件系统可用度马氏建模方法[J]. 仪器仪表学报, 2016, 37(9): 1996-2003.
GENG Yan, GUO Lin-han, WANG Ji-ming, et al. Markov modeling method for availability of two-item system under passivation[J]. Chinese Journal of Scientific Instrument, 2016, 37(9): 1996-2003. (in Chinese)
[13] 王少华,张耀辉,徐隆洋,等. 基于仿真的多部件系统状态维修决策优化方法[J]. 兵工学报, 2017, 38(3): 568-575.
WANG Shao-hua, ZHANG Yao-hui, XU Long-yang, et al. Optimal condition-based maintenance decision-making method of multi-component system based on simulation[J]. Acta Armamentarii, 2017, 38(3): 568-575.(in Chinese)
[14] 樊冬明,任羿,刘林林,等. 基于动态贝叶斯网络的可修GO法模型算法[J]. 北京航空航天大学学报, 2015, 41(11): 2166-2176.
FAN Dong-ming, REN Yi, LIU Lin-lin, et al. Algorithm based-on dynamic Bayesian networks for repairable GO methodology model[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(11): 2166-2176. (in Chinese)
[15] Liu Z K, Liu Y H, Cai B P, et al. Dynamic Bayesian network modeling of reliability of subsea blowout preventer stack in presence of common cause failures[J]. Journal of Loss Prevention in the Process Industries, 2015, 38:58-66.
[16] Cai B P, Liu Y H, Zhang Y W, et al. Dynamic Bayesian networks based performance evaluation of subsea blowout preventers in presence of imperfect repair[J]. Expert Systems with Applications, 2013, 40(18):7544-7554.
[17] 朱正福,李长福,何恩山,等. 基于马尔可夫链的动态故障树分析方法[J]. 兵工学报, 2008, 29(9): 1104-1107.
ZHU Zheng-fu, LI Chang-fu, HE En-shan, et al. The dynamic fault tree analysis method based on Markov chain[J]. Acta Armamentarii, 2008, 29(9): 1104-1107. (in Chinese)
[18] Fort A, Mugnaini M, Vignoli V. Hidden Markov models approach used for life parameters estimations[J]. Reliability Engineering & System Safety, 2015, 136:85-91.
[19] 王开铭,赵峰,曹茜. 基于动态贝叶斯网络的高速铁路牵引变电所可靠性分析[J]. 中国安全生产科学技术, 2016, 12(6): 128-135.
WANG Kai-ming, ZHAO Feng, CAO Qian. Reliability analysis on traction substation of high-speed railway based on dynamic Bayesian network[J]. Journal of Safety Science and Technology, 2016, 12(6): 128-135. (in Chinese)
[20] 高晓光,陈海洋,符小卫,等. 离散动态贝叶斯网络推理及其应用[M]. 北京: 国防工业出版社, 2016: 44-46.
GAO Xiao-guang, CHEN Hai-yang, FU Xiao-wei, et al. Discrete dynamic Bayesian network inference and its application[M]. Beijing: National Defense Industry Press, 2016: 44-46. (in Chinese)
[21] 丛林虎,徐廷学,董琪,等. 基于改进证据理论的导弹状态评估方法[J]. 系统工程与电子技术, 2016, 38(1): 70-76.
CONG Lin-hu, XU Ting-xue, DONG Qi, et al. Missile condition assessment method based on improved evidence theory[J]. System Engineering and Electronics, 2016, 38(1): 70-76. (in Chinese)
[22] 王亮,吕卫民,滕克难. 基于测试数据的长期贮存装备实时健康状态评估[J]. 系统工程与电子技术, 2013, 35(6): 1212-1217.
WANG Liang, LYU Wei-min, TENG Ke-nan. Real-time health condition assessment of long-term storage equipment based on testing data[J]. Systems Engineering and Electronics, 2013, 35(6): 1212-1217. (in Chinese)
[23] Zhang R J, Zhang L L, Dong M X. Multi-state system importance analysis method of fuzzy Bayesian networks[J]. International Journal of Industrial & Systems Engineering, 2015, 21(3):395-414.
[24] Ramirez-Marquez J E, Coit D W. Multi-state component criticality analysis for reliability improvement in multi-state systems[J]. Reliability Engineering & System Safety, 2007, 92(12):1608-1619.
AvailabilityModelingandAnalyzingofMulti-stateControlUnitunderCondition-basedMaintenance
LI Zhi-qiang, XU Ting-xue, GU Jun-yuan, AN Jin, DONG Qi
(Department of Ordnance Science and Technology, Naval Aeronautical University, Yantai 264001, Shandong, China)
A modeling method of control units under condition-based maintenance (CBM) based on multi-state dynamic Bayesian network (DBN)is proposed for describing the dynamic characteristics of system. After defining multi-state components, a state-transition model based on Markov model is established in considering CBM, and absorbing state is introduced. A multi-state DBN model is established to determine the state-transition relationships with non-repair, perfect repair, imperfect repair, CBM and absorbing state. And the conditional probability value is obtained according to the logic relationship of series system and parallel system. A control unit is taken for example. The dynamic fault tree (DFT) and DBN model are established to determine the reliability curves of control unit and its components under different repair modes. And the weak links of reliability design are found through importance analysis. The simulated results show that the control unit under CBM has higher availability than the perfectly and imperfectly repaired control units. The availability of repairable components with degradation states can be predicted, and a maintenance policy can be made accordingly.
ordnance science and technology; dynamic Bayesian network; conditional-based maintenance; perfect repair; imperfect repair; dynamic fault tree; importance analysis
E92
A
1000-1093(2017)11-2240-11
10.3969/j.issn.1000-1093.2017.11.022
2017-04-17
国家自然科学基金项目(51605487);中国博士后科学基金项目(2016M592965);山东省自然科学基金项目(ZR2016FQ03)
李志强(1988—),男,博士研究生。E-mail: 18663813941@163.com
徐廷学(1962—),男,教授,博士生导师。E-mail: yt-xtx@163.com
