深度强化学习在变体飞行器自主外形优化中的应用

温 暖，刘正华，祝令谱，孙 扬

(北京航空航天大学自动化科学与电气工程学院，北京 100191)

深度强化学习在变体飞行器自主外形优化中的应用

温 暖，刘正华，祝令谱，孙 扬

(北京航空航天大学自动化科学与电气工程学院，北京 100191)

基于深度强化学习策略，研究了一类变体飞行器外形自主优化问题。以一种抽象化的变体飞行器为对象，给出其外形变化公式与最优外形函数等。结合深度学习与确定性策略梯度强化学习，设计深度确定性策略梯度(DDPG)学习步骤，使飞行器经过训练学习后具有较高的自主性和环境适应性，提高其在战场上的生存、应变和攻击能力。仿真结果表明，训练过程收敛较快，训练好的深度网络参数可以使飞行器在整个飞行任务过程中达到最优气动外形。

变体飞行器；深度强化学习；气动外形优化

0 引 言

基于配备的智能驱动机构，变体飞行器可以大尺度的改变自身构型。此种性能使其可以替代多种不同型号的飞行器，在多任务飞行中实现全局大包线最优气动外形。正是由于变体飞行器在上述性能上所拥有的巨大发展潜力，使其成为新一代智能飞行器的有效解决方案，这使得变体飞行器的研究达到了一个全新的战略高度，得到了国内外相关机构的广泛重视[1-2]。目前，针对变体飞行器的研究主要集中于结构蒙皮设计[3]与姿态控制[4]等方面。对于如何让飞行器根据任务与环境智能决策变体这方面内容，研究相对较少。

在变体飞行器设计过程中，自然界中的鸟类给予了人类很多启示。如图1(a)所示，鹰在穿越风场时会收缩翅膀，并使其前掠来提高速度。在图1(b)中，鹰又在翱翔时尽量展开翅膀，以达到自身消耗最小的飞翔外形。未来变体飞行器的发展趋势就是智能化与仿生化相结合，飞行器采用智能材料来实现机械柔性结构，从而根据飞行条件、任务与环境的变化，像鸟一样智能改变自身构型以获得最优的飞行性能，如图1(c)和(d)所示。

如何使飞行器在没有人的干预下具有自主决策能力一直是一个难题。对于变体飞行器来说，即使在已经获得当前最优气动外形的情况下，如何根据自身经验和知识来操纵驱动装置使气动外形达到最优仍然是非常困难的。强化学习策略能够有效适应环境的启发,以试错的机制与环境进行交互，通过使累积奖赏最大化的方式来学习到最优策略[5]。因此，强化学习是一种使变体飞行器具有自主决策能力的有效手段。

对于强化学习的研究，学术界一直没有中断过，目前常用的强化学习方法包括蒙特卡罗法、Q学习、SARSA学习、TD学习、策略梯度和自适应动态规划等。强化学习在策略选择的理论和算法方面已经取得了很大的进步，但其中大部分成功的强化学习应用方案均非常依赖于人工特征的选取，且学习结果的好坏更是严重地取决于特征选取的质量[6]。近期深度学习的发展使得对高度结构化的数据进行特征提取成为可能。基于神经网络的深度学习具有较强的感知能力，对于图像分类和语音识别应用效果较好，但是面对实际中的决策判断问题却无能为力；而强化学习具有决策选择能力，但对感知问题束手无策。因此，可将两者有机结合起来搭建深度强化学习框架，从而实现优势互补，为复杂系统的感知决策问题提供新的解决思路。最近，DeepMind团队在Nature上的两篇文献，即深度Q学习网络(Deep Q-network, DQN)在Atari游戏中的应用[7]和AlphaGo在围棋中的对弈[8]，标志着“深度强化学习”作为一种全新的机器学习算法，已经能够使人工智能在视频游戏及棋类博弈中与人类专家相抗衡。但是上述的深度强化学习算法主要还是局限于传统的强化学习框架下，对于离散状态与离散动作具有较好的通用性，却无法处理实际环境中的连续状态与连续动作。文献[9]结合确定性策略方法与DQN，提出了针对于连续控制问题的DDPG方法。近来，最新的算法A3C(Asynchronous advantage actor critic)和UNREAL(Unsupervised reinforcement and auxiliary learning)更是展现了深度强化学习更广泛的前景。

本文以一类外形简化的变体飞行器为研究对象，将原先只应用于简单控制问题的DDPG学习方法应用到变体飞行器的外形优化问题中。首先给出一种简化的变体飞行器外形模型，定义飞行器外形的动态方程、最优气动外形和代价函数。在此基础上，针对此连续状态的控制问题阐述了DDPG算法的基本构成框架和设计流程。在Python+TensorFlow平台下，搭建深度学习训练框架结构，最终利用训练好的深度网络参数验证飞行过程中的实际学习效果。

1 变体飞行器外形模型

本文以一种简化的椭球形变体飞行器为研究对象[10-11]，其由先进的形状记忆合金(Shape memory alloy，SMA)构成，如图2所示。此飞行器通过给定电压调节SMA的形态从而控制自身外形沿椭球轴线方向发生变化。飞行器外形优化的过程就是根据外部的飞行环境和任务来调整其在y轴和z轴方向上的轴长。同时，为了保证整机体积不变，x轴方向上的轴长也会同时发生变化。

y轴和z轴方向上的形变动态与给定电压之间的关系可由非线性差分方程(1)给出

(1)

式中：y和z分别表示椭球形变体飞行器在y轴和z轴方向上的椭球轴长。Vy和Vz分别表示调节SMA在y轴和z轴方向上形变的驱动电压。式(1)中系数的选取参考了文献[10]。且y，z，Vy和Vz取值范围设定为：y,z∈[2,4]，Vy,Vz∈[0,5]。

对应于飞行状态F，y轴和z轴方向上的最优气动外形由式(2)给出

(2)

式中：Sy与Sz表示飞行器具有最优升阻比的气动外形。F从离散状态{0,1,2,3,4,5}中选取，具体取值由当前所处飞行轨迹上的高度与速度所决定。

结合式(1)与式(2)，代价函数C可以表示为

(3)

2 基于深度确定性策略梯度的变体飞行器外形优化学习

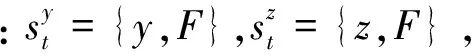
考虑到上述动作空间的连续性问题，本文采用的是强化学习中的确定性策略梯度算法以实现连续控制问题。针对单纯的确定性策略无法探索环境这个缺陷，可以利用Actor-Critic(AC)学习框架实现异策略学习方式，即行动策略与评估策略不是同一个策略方法。行动策略为随机策略，以保证充足的探索。而评估策略为确定性策略，其可以通过梯度计算来实现累计奖赏J的最大化。在AC算法中，可以把策略函数μ(s|θμ)和行为值函数Qπ(s,a|θQ)分别用单独的函数来近似。策略函数μ(s|θμ)作为Actor来进行动作选择，而行为值函数Qπ(s,a|θQ)作为Critic来对策略函数进行评估。而二者均可根据Critic的输出来进行更新。

确定性策略的动作公式为

a=μ(s|θμ)

(4)

与随机策略不同，当式(4)中的θμ(策略函数中的权重因子)确定下来后，在状态为s时，动作是唯一确定的。另外，在行为值函数Qπ(s,a|θQ)评估过程中用的是经典的Q-learning的方法，其中θQ为行为值函数中待逼近的权值参数。AC算法将对动作的Q值估计和策略估计分离，使其能够在探索更多环境状态的同时保持某个确定性策略的学习，从而令整个网络学习变得更容易收敛。

在确定性策略中，作为目标函数的累计奖赏J相对于策略参数θμ的梯度为[9]

(5)

式中：E代表期望值。策略梯度的思想就是沿着使目标函数J变大的方向调整策略参数θμ。

在式(5)基础上，可以得到确定性策略AC算法的更新过程

(6)

(7)

式(6)是利用Q学习值函数逼近的方法更新行为值函数的参数θQ，式(7)是利用确定性策略梯度的方法更新策略的参数θμ。

上面所述的方法为确定性策略梯度(Deterministic policy gradient, DPG)。在DPG基础上可以利用深度神经网络逼近行为值函数Qπ(s,a|θQ)和确定性策略μ(s|θμ)，就成为深度确定性策略梯度(Deep deterministic policy gradient,DDPG)学习算法。

注1. 当利用深度神经网络进行函数逼近的时候，强化学习算法常常不稳定。这是因为，对网络进行训练时往往假设输入的数据是独立同分布的[7]，但强化学习的数据是顺序采集的，数据之间存在马尔科夫依赖性，并非独立同分布。为了打破数据之间的关联性，可以采用“经验回放”方法，将每次进行动作以后得到的“状态-动作-反馈-新状态”保存到缓存中去，训练采用的样本则从这个缓存中随机抽取。利用此种训练技巧，理论上可以打破学习过程中的数据依赖性的。

在训练过程中，由于环境是相对混沌的，用于更新网络的反馈具有很大的噪声，直接训练深度网络会非常容易发散。因此，在DDPG训练学习过程中，本文采用目标网络方法，创建Actor和Critic网络的副本μ-(s|θμ-)，Q-(s,a|θQ-)来计算目标值，然后以τ的比例缓慢跟随原网络更新。如此所得的目标值就会变得相对稳定，非常有利于学习的效果。故更新过程可以变为

(8)

(9)

(10)

综上，DDPG的算法步骤如下：

1)随机初始化Critic深度神经网络Q(s,a|θQ)的权重θQ和Actor的深度神经网络μ(s|θμ)的权重θμ。

2)初始目标网络Q-与μ-的权重θQ-与θμ-。

3)初始化经验回放的缓存区R。

4)重复每一幕。

5)初始化随机过程N以用于行动策略的探索。

6)初始观测得到状态s1。

7)重复步骤8)～16)。

8)根据当前的策略和随机探索选择动作：

at=μ(st|θμ)+Nt

9)执行动作at从而得到奖励rt和新的状态st+1。

10)将(st,at,rt,st+1)存储在缓存区R中。

11)在R中随机选取一组数量为M的(si,ai,ri,si+1)。

12)设定

yi=ri+γQ-(si+1,μθ-(si+1|θμ-)|θQ-)

14)利用所选取样本的策略梯度更新Actor的网络参数

15)更新目标网络

16)直到最大步数和最大幕数。

3 仿真校验

为了验证深度强化学习在变体飞行器外形优化过程中的有效性，本节将上文所提到的DDPG学习算法编程实现，并应用于变体模型(1)、(2)与(3)的飞行器外形优化策略中。基于AC强化学习与深度学习的DDPG算法的架构如图3所示，Critic深度神经网络Q(s,a|θQ)和Actor的深度神经网络μ(s|θμ)均有两个隐藏层，每个隐藏层里有400个神经元，Critic网络采用Relu激活函数，Actor网络则采用tanh激活函数。在Critic网络中，本文将动作Action输入到隐藏层-2中。

训练过程设计如下，对于独立的y轴和z轴分别进行学习优化，步骤1)中的最大幕数设置为200，前100个幕中加入随机动作以进行探索，在后100个幕中将探索去掉，从而进行在线策略利用。每个幕中的最大步数Step设置为500。软件开发平台为：Python2.7+TensorFlow1.0+Cuda8.1+Cudnn5.1，硬件平台采用型号为Nvidia-GTX960的GPU。

每个幕的累积奖赏如图4所示。可以看出,在整个训练学习过程中，学习效果收敛较快，且不加探索的后100个幕的累积奖赏波动不大，表明整个深度学习网络较为稳定。

训练完成后的优化策略验证过程设计如下：变体飞行器的飞行状态F由飞行轨迹决定，其关系如图5所示，将训练后的Actor网络保存下来，并在如图5所示的飞行路径中进行试验。可得到飞行过程中的变体飞行器外形y与z的优化状态，并将本文的DDPG算法与文献[12]中的Multi-Q学习方法进行对比。由图6～7可以看出，DDPG算法的优化效果明显好于Multi-Q学习。这主要是因为传统的Q学习依赖于离散的状态空间和离散的动作空间，对于此变体飞行器外形优化这种连续过程只能采用离散化手段，这会导致最终学习完成后的输出动作为离散值，造成优化精度不高。而DDPG算法采用深度神经网络逼近状态-动作策略,可以计算出连续动作值，使得学习效果较好。

4 结 论

本文针对变体飞行器的外形优化问题，应用近几年较为热门的深度强化学习算法使飞行器通过训练学习具有了自主优化外形的能力，将人工智能方法拓展到飞行器策略优化领域。为了解决传统的强化学习框架不适用于连续控制这个问题，结合确定性策略梯度算法与Actor-Critic框架进行强化学习过程，并将深度神经网络替代原来传统的Actor函数与Critic函数结构，以实现更好的学习效果。仿真结果表明，整个学习过程收敛较快，并且利用训练好的深度网络参数，可以使后期飞行过程中的外形优化效果大幅度提高。

[1] 何墉，章卫国，王敏文，等. 基于多目标控制的变体飞行器切换线性变参数控制器[J]. 控制理论与应用. 2015, 32(11): 1518-1525. [He Yong, Zhang Wei-guo, Wang Min-wen, et al. Switching linear-parameter-varying controller for morphing aircraft based on multi-objective[J]. Control Theory amp; Applications. 2015, 32(11): 1518-1525.]

[2] 江未来, 董朝阳, 王通,等. 变体飞行器平滑切换LPV鲁棒控制[J]. 控制与决策, 2016, 31(1):66-72. [Jiang Wei-lai, Dong Chao-yang, Wang Tong, et al. Smooth switching LPV robust control for morphing aircraft[J]. Control and Decision, 2016, 31(1):66-72.]

[3] 杜善义，张博明. 飞行器结构智能化研究及其发展趋势[J]. 宇航学报, 2007, 28(4): 773-778. [Du Shan-yi, Zhang Bo-ming. Status and developments of intelligentized aircraft structures[J]. Journal of Astronautics, 2007, 28(4): 773-778.]

[4] 董朝阳，江未来，王青. 变翼展飞行器平滑切换LPV鲁棒H∞控制[J]. 宇航学报. 2015(11): 1270-1278. [Dong Chao-yang, Jiang Wei-lai, Wang Qing. Smooth switching LPV robust H-infinity control for variable-span vehicle[J]. Journal of Astronautics, 2015(11): 1270-1278.]

[5] Sutton R S,Precup D, Singh S. Between MDPs and semi-MDPs: a framework for temporal abstraction in reinforcement learning[J]. Artificial Intelligence, 1999, 112(1-2): 181-211.

[6] 赵冬斌, 邵坤, 朱圆恒, 等. 深度强化学习综述:兼论计算机围棋的发展[J]. 控制理论与应用, 2016, 33(6):701-717. [Zhao Dong-bin, Shao Kun, Zhu Yuan-heng, et al. Review of deep reinforcement learning and discussions on the development of computer go[J]. Control Theory and Applications, 2016, 33(6):701-717.]

[7] Mnih V, Kavukcuoglu K, Silver D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(7540):529.

[8] Silver D, Huang A, Maddison C J, et al. Mastering the game ofgo with deep neural networks and tree search[J]. Nature, 2016, 529(7587): 484.

[9] Lillicrap T P, Hunt J J, Pritzel A, et al. Continuous control with deep reinforcement learning[J]. Computer Science, 2015, 8(6): 187-200.

[10] Valasek J, Tandale M D, Rong J. A reinforcement learning-adaptive control architecture for morphing[J]. Journal of Aerospace Computing Information amp; Communication, 2005, 2(4): 174-195.

[11] Valasek J, Doebbler J, Tandale M D, et al. Improved adaptive-reinforcement learning control for morphing unmanned air vehicles[J]. IEEE Transactions on Systems Man amp; Cybernetics Part B, 2013, 38(4): 1014-1020.

[12] Duryea E, Ganger M, Hu W. Exploringdeep reinforcement learning with multi-Q-learning[J]. Intelligent Control and Automation, 2016, 7(4): 129-144.

DeepReinforcementLearningandItsApplicationonAutonomousShapeOptimizationforMorphingAircrafts

WEN Nuan, LIU Zheng-hua, ZHU Ling-pu, SUN Yang

(School of Automation Science and Electrical Engineering, Beihang University, Beijing 100191, China)

This paper considers a class of simplified morphing aircraft and autonomous shape optimization for aircraft based on deep reinforcement learning is researched. Firstly, based on the model of an abstract morphing aircraft, the dynamic equation of shape and the optimal shape functions are derived. Then, by combining deep learning and reinforcement learning of deterministic policy gradient, we give the learning procedure of deep deterministic policy gradient(DDPG).After learning and training for the deep network, the aircraft is equipped with higher autonomy and environmental adaptability, which will improve its adaptability, aggressivity and survivability in the battlefield. Simulation results demonstrate that the convergence speed of learning is relatively fast, and the optimized aerodynamic shape can be obtained autonomously during the whole flight by using the trained deep network parameters.

Morphing aircrafts；Deep reinforcement learning；Aerodynamic shape optimization

V249.1

A

1000-1328(2017)11- 1153- 07

10.3873/j.issn.1000- 1328.2017.11.003

2017- 06- 20;

2017- 09- 13

国家自然科学基金(61305132，61563041)；航空科学基金(20135751040)

温暖(1988-)，男，博士生，主要从事智能变体飞行器的控制研究。

通信地址：北京航空航天大学新主楼(100083)

电话：(010)82338658

E-mail: max_buaa3@163.com

刘正华(1974-)，男，博士，副教授，主要从事飞行器控制，系统仿真，高精度运动控制等方向的研究。本文通信作者。

通信地址：北京航空航天大学新主楼(100083)

电话：(010)82338658

E-mail: lzh@buaa.edu.cn