电磁场中磁感应强度的计算及解析

黄丹

（吉林建筑大学城建学院，吉林长春130000）

电磁场中磁感应强度的计算及解析

黄丹

（吉林建筑大学城建学院，吉林长春130000）

电磁场的计算问题，主要归结为电场强度和磁感应强度的计算.其中电场强度的计算问题已经有很多文献报道了，而对于磁感应强度的计算还没有文献报道.本文主要阐述了稳恒磁场中磁场强度的几种计算方法，并通过典型的例题，对毕奥-萨伐尔定律法和安培环路定理法的解题步骤和适用范围做了详细的讨论.

磁感应强度；毕奥-萨伐尔定律；安培环路定理

磁场是电磁场的重要组成部分，是磁体及运动电荷周围空间存在的一种特殊物质，磁场与实物不同，它不是由分子和原子组成的，但磁场是客观存在的.磁感应强度是描述磁场性质的一个重要物理量，掌握各种求解磁感应强度的方法是学好电磁学的基础.本文主要对稳恒磁场中磁感应强度的计算方法进行归纳总结，并通过例题解析，阐明了毕奥-萨伐尔定律和安培环路定理求磁感应强度的思路和方法.

1 磁感应强度矢量的计算方法

磁感应强度的计算方法主要分为以下四种：

（2）毕奥-萨伐尔定律法；

（3）安培环路定理法.

本文重点讨论第（2）、（3）种方法.

2 毕奥-萨伐尔定律

毕奥-萨伐尔定律是计算稳恒磁场中磁感应强度的一种重要方法，它是由法国物理学家毕奥和萨伐尔等人对载流导体产生的磁场做了大量的实验研究，并在数学家拉普拉斯的帮助下总结出来的[1].定律的内容是任意一段电流元Idl→在真空中某一点产生的磁感应强度的大小与电流元的大小dB及电流元和它到该点的位置矢量r之间的夹角的正弦乘积成正比，与位矢大小的平方成反比方向相同，这一结论称为毕奥-萨伐尔定律[2].其数学表达式分为矢量式和标量式，（1）矢量式（2）标量式

利用此定律可以计算任意一段载流导线在其空间任意一点产生的磁感应强度，进而得到其周围的磁场分布情况.具体的解题步骤为：

（1）将载流导体分割成无限多个电流元,并用右手定则判断每一段电流元在所求点的磁感应强度的方向.

（3）利用磁感应强度的叠加法，求出所有电流元在该点所产生的总磁感应强度

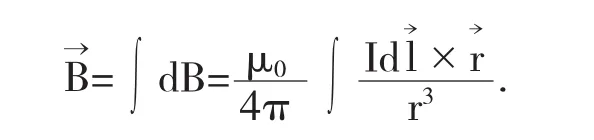
在实施（3）时有两点需要注意：①.若磁场为二维或者三维场时，则需将先正交分解，然后再积分；②.如果被积分的含有多个变量，则需利用数学中的三角函数关系，将多个变量统一成一个变量，然后再积分.

下面列举两道经典例题，具体分析毕奥-萨伐尔定律的应用.

例2.1求有限长载流直导线周围的磁场.如图1所示，在真空中有一通有电流为I的长直导线C D，直导线长为L，试求距此导线为r0的一点P处的磁感应强度.

图1

解析建立如图所示的坐标轴，将载流导体分割成无限多个电流元，每一段电流元在P点的磁感应强度的方向都是沿O x轴的负方向；任取一电流元Idz，根据毕奥—萨伐尔定律，此电流元在点P所激发的磁感应强度的大小为dB=

式中θ为电流元与位矢之间的夹角.由于直导线上各个电流元的的方向都相同.因此点P的磁感应强度的大小就等于各个电流元的磁感应强度之和，用积分表示，有

由于式中含有多个变量，利用数学中的三角函数关系，将多个变量统一成一个变量，然后再积分.从图可以看出z,r和θ之间有如下关系：z=-r0cotθ，r=r0/sinθ.

于是，dz=r0dθ/sin2θ，因而上式可写成

若载流直导线为“无限长”直导线，那么，可近似取θ1=0，θ2=π.这样由上式可得

这就是“无限长”载流直导线附近的磁感应强度，它表明，其磁感应强度与电流成正比，与场点到导线的垂直距离成反比，此结论与毕奥—萨伐尔早期的实验结果是一致的.

例2.2圆形载流导线轴线上的磁场.设在真空中，有一半径为的载流导线，通过的电流为，通常称作圆电流.试求通过圆心并垂直于圆形导线平面的轴线上任意点处的磁感应强度.

图2

解析建立如图所示的坐标轴，将载流导线分成多个电流元，每一段电流元在P点的磁感应强度的方向都是不同的；在圆上任取一电流元I dl→，根据毕奥—萨伐尔定律，该电流元在P处的磁感应强度大小为

由于每一段电流元在P点产生的dB的方向都不同,因此需将dB先正交分解，然后再积分.取d分解成两个分量：一个沿O x轴的分量dBx=dB cosα；另一个是垂直于O x轴的分量dB⊥=dBsinα.考虑到圆上任一直径两端的电流元对O x轴的对称性，故所有电流元在点P处的磁感应强度的分量d B⊥的总和应等于零.所以，点P处的磁感应强度的数值为

由于cosα=R/r,所以得到圆形载流导线轴线上的磁场为

的方向垂直于圆形导线平面沿O x轴的正向.

利用毕奥—萨伐尔定律，原则上可以求解任意电流系统产生的磁场问题，但一般计算较为复杂.当电流分布具有某种对称性时，利用安培环路定理能很简单地算出磁感应强度.

3 安培环路定理

安培环路定理是另一种求解稳恒磁场中磁感应强度的重要方法.目前有多篇文献阐述了安培环路定理的推导过程[3-5]，这里不再给出此定理的推导，直接给出安培环路定理的内容.在真空的稳恒磁场中，磁感应强度B→沿任一闭合路径的线积分（即的环流），等于真空中的磁导率μ0乘以该闭合路径所包围的各电流的代数和，这就是安培环路定理[6].数学表达式为此定理仅适用于具有对称性的稳恒电流产生的磁场.

二进制粒子群中，为了实现上述的概率选择，将速度vid转换到概率区间[0,1]的目的，引入函数Sigmoid，对其定义为：

安培环路定理的具体求解步骤：（1）对电流和磁场的分布进行对称性分析；（2）选取积分回路，所选回路上各点的磁感应强度都相等；（3）应用安培环路定理解题.下面举例说明如何利用安培环路定理求解磁感应强度.

例3.1求无限长载流圆柱体内外的磁场.（已知圆柱体的底面半径为R，恒定电流I沿轴线方向流动，且电流在截面积上的分布是均匀的）.

解析由于圆柱形导体很长，那么在导体的中部，磁场的分布可视为是对称的；如图3所示，设点P离圆柱体轴线的垂直距离为r，选取半径为r的圆环为积分回路，由于对称性，在以r为半径的圆周上的值相等，方向都是沿圆的切线.

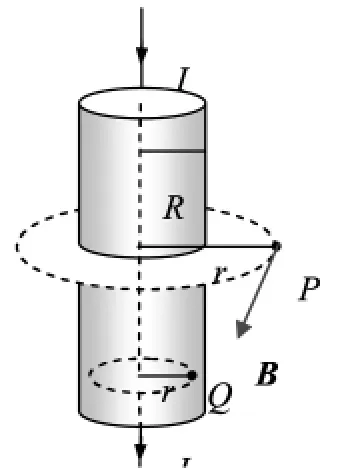
图3

当r＞R时：根据安培环路定理有

当(r＜R)时：根据安培环路定理有

由结果可以看出：圆柱体内部B与r成正比,在圆柱体外部B与r成反比.

例3.2求载流螺绕环内的磁场.（如图4所示，已知环上线圈的总匝数为N，电流为I）.

图4

解析由于螺绕环内的磁感线都是一些同心圆，故具有对称性；通过P点取半径为r的圆环作为积分回路，由于线上任一点的磁感应强度的量值相等，方向都与dl→同向，故得的环流为：

由安培环路定理：B2πr=μ0NI

4 总结

本文简单介绍了四种求解磁感应强度的方法，重点介绍毕奥-萨法尔定律法和安培环路定理法，并举例说明了这两种方法的解题步骤和适应范围.毕奥—萨伐尔定律是计算磁感应强度最普遍、最基本的方法，而安培环路定理是在毕奥-萨法尔定律的基础上加上无限长载流直导线等条件推导出来的，因此安培环路定理的应用受到了很大限制，但是当遇到电流具有对称性的题，应用安培环路定理来求解是很方便的.

〔1〕姜广军，程彦明.大学物理学（下册）[M].北京：机械工业出版社，2013.64.

〔2〕马文蔚.物理学教程（上册）[M].北京：高等教育出版社，2001.290.

〔3〕付静，姜广军，袁明霞.普通物理学中磁场安培环路定理的证明[J].长春工业大学学报，2012（33）:709-711.

〔4〕徐恩生，孙丽媛.稳恒磁场安培环路定理的论述与推导[J].沈阳航空工业学院学报，2005（22）:83-84.

〔5〕冯晓娟，强稳朝，张频，张建国.磁场安培环路定理证明的新方法[J].物理与工程，2010（20）:13-16.

〔6〕马文蔚，周雨青，解希顺.物理学教程（下册）[M].北京：高等教育出版社，2010.90.

O441

A

1673-260X（2017）11-0011-03

2017-07-06