一类n维椭球体上的n重积分及估计
2017-11-30杨海涛
孙 燕,杨海涛
(内蒙古民族大学 数学学院,内蒙古 通辽 028043)
一类n维椭球体上的n重积分及估计
孙 燕,杨海涛
(内蒙古民族大学 数学学院,内蒙古 通辽 028043)

n维椭球体;n重积分;重积分不等式
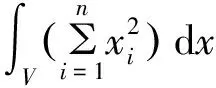
1 主要结论

(1)
证明n维球坐标变换[6]:
x1=rcosφ1,
x2=rsinφ1cosφ2,
……
xn-1=rsinφ1sinφ2…sinφn-2cosφn-1,
xn=rsinφ1sinφ2…sinφn-2sinφn-1
(2)
其中:0≤r≤1,0≤φ1,φ2,…,φn-2≤π,0≤φn-1≤2π.
那么n维球坐标变换所对应的Jacobi行列式为
J=rn-1sinn-2φ1sinn-3φ2…sin2φn-3sinφn-2.
(3)
(4)
(5)
则:

定理2 设a=(a1,a2,…,an),b=(b1,b2,…,bn),bigt;0,i=1,2,…,n,a,b∈Rn,n维椭球体Ω.
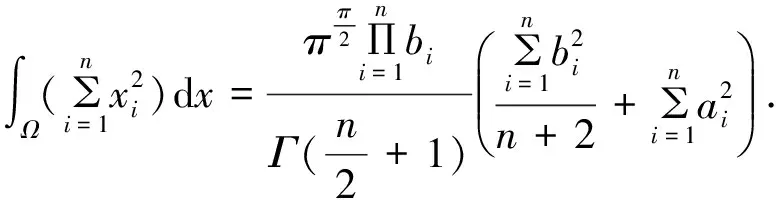
(6)



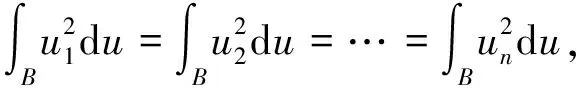

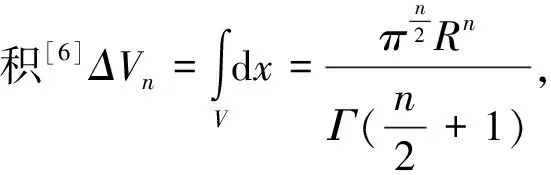
所以:

(7)
由定理2,a1=a2=…=an=0,b1=b2=…=bn=R,代入式(6)可得式(7).
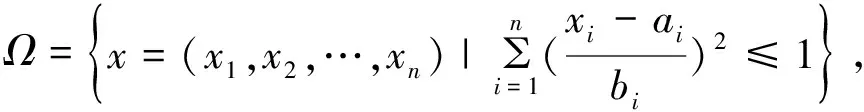

(8)
证明广义椭球坐标变换:
x1=b1rcosφ1+a1,
x2=b2rsinφ1cosφ2+a2,
……
xn-1=bn-1rsinφ1sinφ2…sinφn-2cosφn-1+an-1,
xn=bnrsinφ1sinφ2…sinφn-2sinφn-1+an
(9)
Ω变换为∑={(r,φ1,φ2,…,φn-2,φn-1)|0≤r≤1,0≤φ1,φ2,…,φn-2≤π,0≤φn-1≤2π},
有
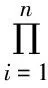
(10)

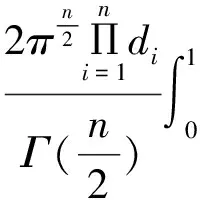
2 应用

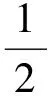
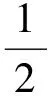
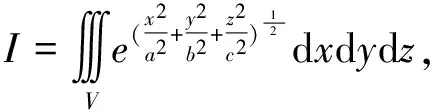
由定理3n=3,ai=0,i=1,2,3,b1=a,b2=b,b3=c代入式(8),

例3 估计五重积分的值
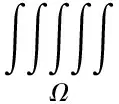
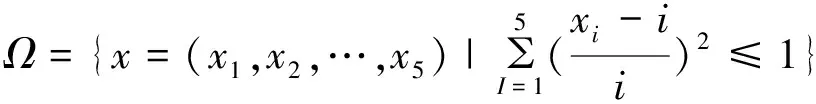
由定理3n=5,ai=bi=i,i=1,2,3,4,5代入式(8),

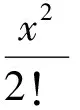
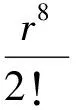
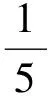
0.389 946π2lt;I2lt;0.390 028π2
本文结果可用于计算均匀n维椭球体、n维球体的质量、体积、静矩、惯矩及离心力等.
[1] SUN YAN,YANG HAITAO,QI FENG.Some inequalities for multiple integrals on then-Dimensional ellipsoid,spherical shell,and ball[J]. Abstract and Applied Analysis,Volume 2013,Article ID 904721,7 pages.
[2] 孙燕,关于维球体上的一个重积分不等式[J].内蒙古民族大学学报(自然科学版),2012,27(4),394-396.
[3] FENG Q I,Inequalities for a multiple integral[J].Acta Math Hungar,1999,84(1/2):19-26.
[4] 匡继昌.常用不等式[M].4版.济南:山东科学技术出版社,2010.
[5] 孙燕,杨海涛.几个重积分不等式的证明[J],内蒙古民族大学学报,2012,18(2):9-10.
[6] 华东师范大学数学系.数学分析(上下册)[M].3版.北京:高等教育出版社,2001:264
[7] 叶其孝,沈永欢.实用数学手册[M].2版.北京:科学出版社,2006.
责任编辑:时凌
AClassofn-MultipleIntegralonthen-DimensionalEllipsoidandItsEstimation
SUN Yan,YANG Haitao
(College of Mathematics,Inner Mongolia University for Nationalities,Tongliao 028043,China)
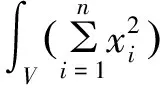
n-dimensional ellipsoid;n-multiple integrals;multiple integrals inequality
2017-04-19.
国家自然科学基金资助项目(11561052).
孙燕(1964-),女,副教授,主要从事分析理论及不等式的研究.
1008-8423(2017)04-0409-04DOI:10.13501/j.cnki.42-1569/n.2017.12.012
0718
A
