透明物体渲染算法在火星环绕器在轨可视化中的应用

吴振中

（南京航空航天大学 电子信息工程学院，江苏 南京 211106）

透明物体渲染算法在火星环绕器在轨可视化中的应用

吴振中

（南京航空航天大学 电子信息工程学院，江苏 南京 211106）

针对火星环绕器的在轨可视化，需要考虑轨道与透明火星发射天线范围之间的复杂交互情况，采用普通的单一处理透明物体的油画家算法和深度缓存算法已经不能满足实际可视化功能的需要，并且不能利用好性能日益强劲的GPU。文章通过对无序场景下的半透明物体的渲染算法研究，针对火星环绕器在轨可视化实现中的实际需求，分别使用了深度缓存算法、油画家算法、加权平均值算法和深度剥离算法，实现了火星环绕器在轨可视化功能。通过工程实践结果的比较和各个算法原理的优缺点分析比对，确定了深度剥离算法在透明物体和非透明物体同一场景下联合渲染中的效果，最终实现了火星环绕器在轨可视化功能。

OpenGL；透明；渲染；α混合；深度剥离

深空探测已经成为21世纪人类的三大航天活动之一。对于任何一个国家或者民族来说，掌握航空航天领域的尖端技术有助于增强民族的自豪感和凝聚力，使整个民族都迸发出科学探索的热情[1]。在火星深空探测任务中，如何实时模拟出火星环绕器在轨情况，对于火星深空探测任务来说，也具有非常重要的实际意义。

然而在火星环绕器在轨可视化功能的实现中，如何实时处理好火星地面站发射天线范围与环绕器发射天线交互范围，成了一大难题。因为这里面涉及非透明物体和透明物体联合渲染的问题。

透明是一种非常重要的渲染实现效果，普通场景中应用了透明效果后，可以非常明显地提高普通场景的真实体验和整个可视化功能的效率。

传统上解决透明物体和非透明物体渲染的算法主要有深度缓存[2]和油画家算法[3]，但由于各种各样的原因，这并不是解决这一难题的最佳手段。最近几年流行的加权平均值算法和深度剥离算法[4]可以比较有效地解决这一难题。

本文在分析对比这4种不同的渲染算法的基础上，实际将算法应用在了火星环绕器在轨可视化的工程中，并在实践中得出结论，深度剥离算法在解决透明物体和非透明物体渲染方面，有着独到的优势。

1 透明物体渲染算法分析

开放图形库（Open Graphics Library，OpenGL）初学者总会面临一个现象，那就是进行透明物体渲染时，得到的并不是自己想要的效果。这是因为渲染三维场景时，会根据距离摄像头的远近，有选择地在屏幕上展现三维场景。最主流的处理透明物体和非透明物体渲染的几种算法如下所示。

1.1 深度缓存

在计算机的图形学中，可见性问题主要是决定了在渲染场景中，究竟是哪一部分可见的具体情况。而深度缓存是可见性问题的一个解决方法。

深度缓存是在三维图形中处理图像深度坐标的过程，这个过程可以在硬件中，也可以在软件中完成。其中深度就是三维图形距离摄像机的距离，深度缓存就负责存储三维图形中每个像素点的深度大小。而我们在实际渲染的过程中，就根据物体缓存的深度大小来决定是否需要绘制该物体。

然而，深度缓存也有自己无法解决的问题，那就是本文在火星环绕器在轨可视化过程中实际面临的问题，即半透明物体如何正确的渲染。深度缓存在本质上是无法解决这一难题。

1.2 油画家算法

油画家算法本质上非常简单明了，就是针对场景中的所有透明物体和不透明物体，按照离摄像机的远近，也就是深度排序，先画远处再画近处，从而达到了正确渲染的效果。这样确实可以解决深度缓存中的无法按照正确排序渲染物体的情况。但是油画家算法也存在着本质性的难题。

火星环绕器在轨可视化过程中，也面临着透明物体与不透明物体同时渲染的难题。目前传统的两种处理算法并不能有效的帮助到我们。这时候，我们可以考虑两种更为有效精确的算法。

1.3 加权平均值算法

加权平均值算法是NVIDIA公司的Bavoil等[5]提出来的关于无序透明物体渲染的新算法。该算法的核心思想在于，对于某个位置上的像素点而言，如果所有物体在该像素点上的颜色都是相同的话，那么渲染结果和渲染的顺序无关，直接渲染就可以了。如果各个物体的颜色不相同的话，我们使用各个物体在该像素点上不同颜色的不透明度作为权重，将它们的平均值计算出来。

针对各个颜色平均值的计算问题，加权平均值算法通常的做法是先使用16位精度的浮点数来存储同一像素点上各个颜色的叠加值，并保存不同颜色的总个数。在最后全屏处理的过程中，利用不透明度的权重，对之前存储的结果进行计算。最后算出颜色平均值C：

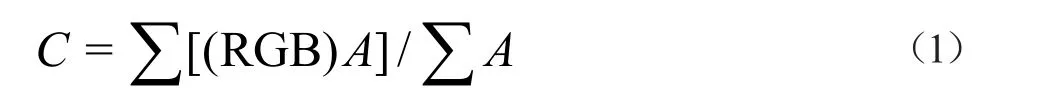
平均不透明度A则是通过对不透明度的总和求平均值的方法求得的：

最终颜色Cdst就可以根据C,A,n以及背景颜色Cbg求出：

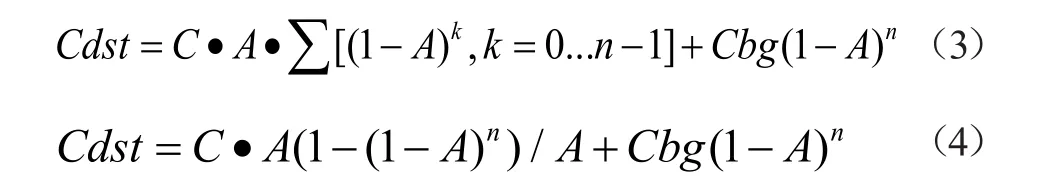
加权平均值算法虽然效率很高，并且速度不慢，但是却有着本质上的不足，那就是算法仅仅只是一个渲染的近似结果，而不是一个精确的值。所以在不是特别追求精确效果的游戏开发中，该算法应用较为广泛。

1.4 深度剥离算法

深度剥离算法是由NVIDIA公司的Everitt[6]提出的一种用来对深度值进行排序的技术，其可以很好地解决不透明物体与透明物体之间的渲染问题。

深度剥离算法的基本原理是通过使用标准的深度检测使场景中的距离摄像头最近的点，也就是深度最小的像素点先被渲染出来。然后进行第2轮的渲染，将离摄像头第二近距离的所有像素点都缓存下来，就这样以此类推，通过多轮渲染的手段，将场景的深度值一层一层的剥离，缓存下来。最后对缓存下来的一层一层的颜色值，按照从后往前的次序来进渲染，从而可以得到正确的透明物体和非透明物体在同一场景的渲染效果。具体剥离的过程如图1所示。

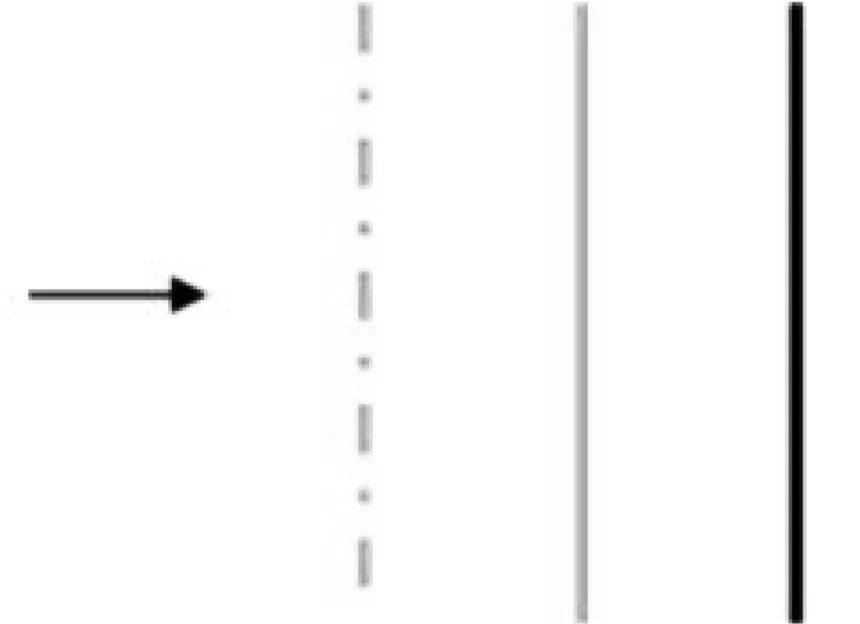
图1 深度剥离算法过程显示

在渲染过程中，深度剥离算法是通过NVIDIA公司开发的阴影映射技术来实现对像素点的剥离的目的[7]。阴影映射的原理是这样的，首先要去判断一个像素点是否在阴影之中。如果一个像素点和光源之间没有任何物体遮挡的话，就默认该像素点没有处于阴影之中，反之则处于阴影状态。阴影映射就是用来存储每个像素点是否存在于阴影状态的信息[8]。

1.5 算法优缺点对比分析

上述分析了4种不同算法的优劣性，其中深度缓存和油画家算法是最不可取的。根据不同算法的时间复杂度和空间复杂度，对算法进行列表评估如表1所示。

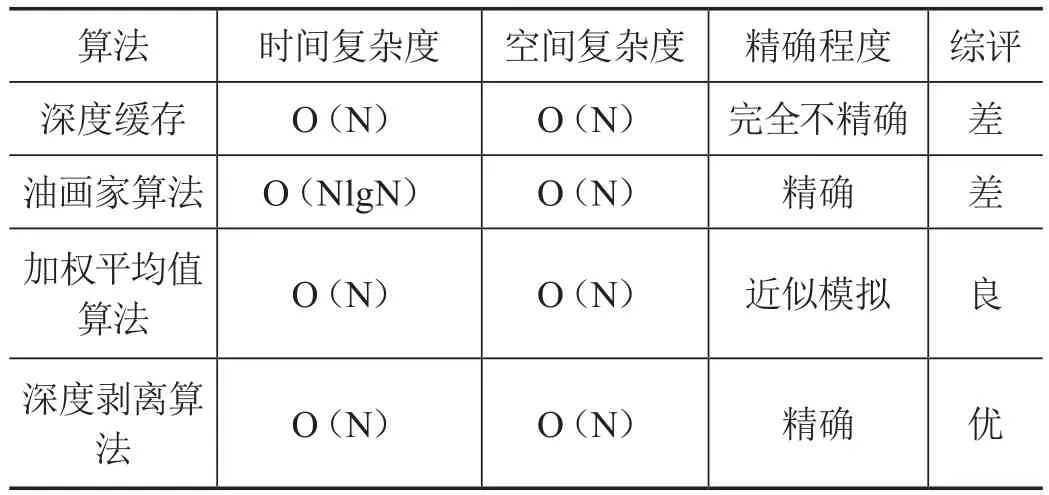
表1 渲染算法性能对比表

结合上表，容易得出深度缓存缺点在于不能精确渲染场景，油画家算法缺点在于算法复杂度过大，加权平均值算法只能做到近似模拟，只有深度剥离算法可以保证效率的同时，做到精确渲染所需场景。

2 工程应用结果比较

最后关于非透明物体和透明物体之间的联合渲染算法的选择上。由于一直被业界使用的深度缓存算法和油画家算法都存在着自身无法避免的缺点。本工程主要选择了上述的加权平均值算法和深度剥离算法分别进行实现，并展示最后火星环绕器在轨可视化的最后效果图。

2.1 加权平均值算法实现

加权平均值算法本质上是根据颜色的不透明度计算各个物体在同一像素点的平均值。火星环绕器在轨可视化使用OpenGL的时候，同时使用了OpenGL着色语言（OpenGL Shading Language，GLSL）。GLSL在图形卡的地面动力装置（Ground Power Unit，GPU）上面执行，取代了OpenGL流水线中固定渲染管线的一部分[9]。

首先为了渲染出不同的透明级别，需要开启OpenGL的混合功能[10-11]。除此之外，还需要让OpenGL通过GLSL着色器语言，按照源颜色向量、目标颜色向量、源因子和目标因子的Alpha值来进行计算，最终输出结果。OpenGL恰好也提供了相应的接口函数，来供我们使用。

需要注意到的是，glBlendFunc函数接受两个参数，来分别设置源和目标因子[12]。OpenGL已经通过C语言宏定义的方式，为我们定义了很多选项。而我们需要半透明物体的渲染效果，直接选用对应的宏定义，就可以实现了，火星环绕器在轨可视化功能效果如图2所示。

2.2 深度剥离算法实现

相比较加权平均值算法而言，深度剥离算法的原理更为复杂。但是相应工程上的实现却不是那么难以做到。

图2 加权平均值算法在工程中应用

OpenGL EXT扩展又可以被称为是OpenGL结构评审委员会（Architecture Review Board，ARB）扩展[13]，而我们需要的深度剥离算法就在ARB扩展中实现了。

3 结语

通过不同透明物体渲染算法实现效果图的对比，可以很明显地看出加权平均值算法在透明物体和非透明物体渲染中并不是完全精确的渲染效果。虽然深度剥离算法实现的消耗更大一些，但是在火星环绕器在轨可视化的工程中，相比于消耗来说，正确的渲染出火星地面站发射天线范围与环绕器发射天线发射范围才是关键。

通过火星环绕器在轨可视化的工程实现运用，可以看出深度剥离算法在非透明物体和透明物体场景渲染上的优势，是一种实现简单、效果极佳的算法。

[1]叶培健，彭兢.深空探测与我国深空探测展望[J].中国工程科学，2006（10）：13-18.

[2]Wikipedia.Z-buffering[EB/OL].（2017-09-27）[2017-10-25].https://en.wikipedia.org/wiki/Z-buffering.

[3]Wikipedia.Painter’s algorithm[EB/OL].（2017-11-20）[2017-10-25].https://en.wikipedia.org/wiki/Painter%27s_algorithm.

[4]罗月童，薛晔，孙静.基于深度剥离的透明渲染技术及其应用[J].中国仪器仪表学会第九届青年学术会议论文集，2007（1）：593-597.

[5]BAVOIL L，MYERS K.Order independent transparency with dual depth peeling[J].Nvidia Opengl Sdk，2008（8）：1036-1047.

[6]EVERITT C.Interactive Order-Independent Transparency[J].White Paper，2001（8）：491-503.

[7]WILLIAMS L.Cating curved shadows on curved surfaces[D].New York：New York Institute of Technology，2000.

[8]GitHub.GLFW[EB/OL].（2016-08-18）[2017-10-25].http://www.glfw.org.

[9]李蕊，周名.基于OpenGL图形引擎的设计与实现[J].电脑知识与技术，2014（25）：34-35.

[10]邱伟，李心鹏，王晓斌.基于OpenGL的三维模型渲染新方法[J].遥测遥控，2016（5）：12-16.

[11]叶帅，游有鹏，邢永彦.基于OpenGL的三维模型交互控制研究[J].机械设计与制造工程，2015（44）：15-16.

[12]GitHub.欢迎来到OpenGL的世界[EB/OL].（2016-08-18）[2017-10-25].https://learnopengl-cn.github.io.

[13]Wikipedia.OpenGL Architecture Review Board[EB/OL].（2017-09-27）[2017-10-25].https://en.wikipedia.org/wiki/OpenGL_Architecture_Re view_Board.

Application of transparent object rendering algorithm in visualization of Mars satellite track

Wu Zhenzhong
（Electronic and Information Engineering College, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China）

In view of the orbit visualization of the Mars satellite, it is necessary to consider the complex interaction between the track and the transparent Mars transmit antenna range. The use of ordinary single-processing transparent objects of the Painter’s algorithm and Z Buffer algorithm has been unable to meet the needs of the actual visualization, can not take advantage of the increasingly powerful GPU performance. In this paper, based on the study of the rendering algorithm of translucent objects in the disordered scene, the Z Buffer algorithm, the Painter’s algorithm, the weighted average algorithm and the depth peeling algorithm are used to realize the actual requirement of the orbit visualization of the Mars Satellite. Through the comparison of the results of engineering practice and the analysis of the advantages and disadvantages of each algorithm, the effect of the depth peeling algorithm in the joint rendering of transparent objects and non-transparent objects in the same scene is determined, and the on-orbit visualization implementation of the Mars satellite is realized.

OpenGL; transparency; rendering; alpha-blending; depth peeling

吴振中（1993— ），男，江苏淮安人，硕士研究生；研究方向：信道建模，可视化。