关于计算二重积分的几种方法

都俊杰 长江大学工程技术学院

关于计算二重积分的几种方法

都俊杰 长江大学工程技术学院

二重积分是高等数学的重点，也是难点，计算较为繁琐，基本的有直角坐标和极坐标计算，但有的二重积分需要一定的技巧才能求出．可利用积分区域和被积函数的对称性巧妙解决，讨论了几类解决二重积分方法。

二重积分 二次积分 直角坐标系 极坐标系

二重积分的计算是高等数学中多元函数积分学重要的一部分，熟练的掌握二重积分的计算技巧很重要。计算二重积分的一般原则是将重积分化为两次定积分来计算，但是由于被积函数的复杂性及积分区域的多样性，计算二重积分就要采取多种方法。有直角坐标系计算二重积分，极坐标系下计算二重积分，利用对称性计算二重积分等等。下面分别就这三个方面介绍计算二重积分的方法，对每种方法给出相应的求解思路，并举出典型的实例，便于读者更好地理解和掌握这些方法，达到事半功倍、举一反三的学习效果。

1 直角坐标系下计算二重积分，将积分区域D分为两种基本情况。

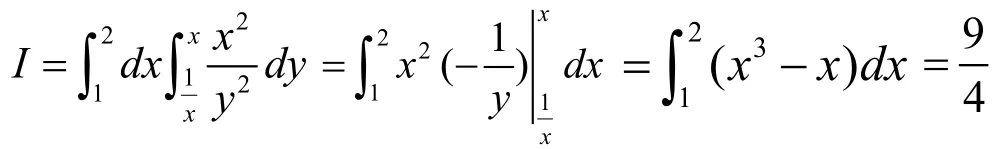
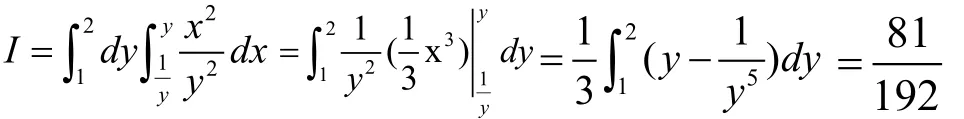
2 极坐标系下计算二重积分

当被积函数和积分区域D的边界曲线为较简单函数时，常考虑用极坐标来计算二重积分。这样就会遇到两个问题：一个问题是如何把被积函数化为极坐标形式；另一个问题是如何把面积元素化为极坐标形式。这两个问题都是容易解决的，当被积函数或者积分区域D中含有时可以用极坐标来计算二重积分。直角坐标与极坐标的转换公式：

3 特殊方法计算二重积分

①利用对称性计算二重积分，和定积分的计算一样，对积分区域具有一定的对称性且被积函数为奇函数或偶函数的二重积分，利用对称性可以大大简化二重积分的计算过程．下面给出对称性定理。

解：利用函数的奇偶性及积分区域的对称性可以简化计算，有

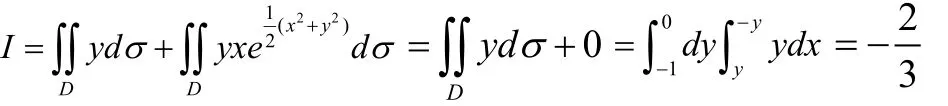
解：利用轮换对称性，有

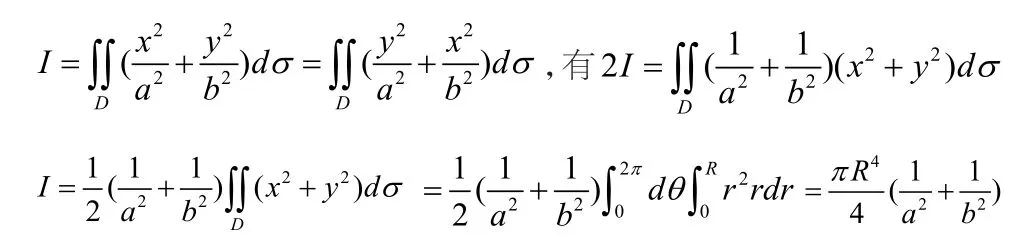
②交换积分次序计算二重积分，对于有些特殊类的函数，计算二重积分可以采取交换积分次序简化计算

解：此函数的积分区域很简单，当直接计算是算不出结果的，可以交换一下次序，有

③分段函数计算二重积分，关于分段函数二重积分的计算问题是学生学习的一个难点，为广大师生所关注，但在大部分教材中，并没有明确指出分段函数二重积分的计算方法．此类问题的一般做法是：(1)画出积分区域的草图；(2)由被积函数的分段点把积分区域分成如干部分区域，使得在每个部分区域中的被积函数表达式明确；(3)利用二重积分的区域可加性，进行计算。

④利用几何意义计算二重积分也是我们常用的方法，二重积分的几何意义就是曲顶柱体（以积分区域D为底，以被积函数为曲顶的柱体）体积的代数和。

[1]同济大学应用数学系；高等数学【M】；北京，高等教育出版社。

[2]杨波，王安平；高等数学；武汉，华中科技大学出版社，2017。

[3]张景中．数学与哲学【M】；北京，中国少年出版社，2006，8：25 ～ 37。

[4]邓乐斌，初等积分中的常见问题【M】；北京。科学出版社，2009。

[5]徐森，浅谈二重积分下的分部积分法的应用；科技视界，2015。

长江大学工程技术学院基金2017ky10。

都俊杰（1981—），女，吉林长春人，副教授，研究方向：应用数学。

0712．2

A