地形分析中栅格中间层构建的尺度适应性
2017-11-29张立朝张合朝
张立朝,赵 鹏,张合朝
(1. 河南省测绘地理信息局, 河南 郑州 450003; 2. 信息工程大学地理空间信息学院,河南 郑州 450052; 3. 河南省科源测绘中心,河南 郑州 450003)
地形分析中栅格中间层构建的尺度适应性
张立朝1,赵 鹏2,张合朝3
(1. 河南省测绘地理信息局, 河南 郑州 450003; 2. 信息工程大学地理空间信息学院,河南 郑州 450052; 3. 河南省科源测绘中心,河南 郑州 450003)
栅格中间层是指在地形分析中由DEM、DSM、矢量数据等原始数据,经过一系列栅格运算获取且可以重用的基础栅格层。本文系统研究了栅格中间层构建的尺度适应性,定义了范围、比例尺、分辨率和分析4种尺度,并确定了范围、比例尺和分辨率尺度的确定原则;特别对于分析尺度,通过地貌因子计算进行了切线、剖面曲率栅格层分析尺度适宜性试验,分析了曲率计算中适宜的算法和分析尺度,保证了地形基础因子栅格中间层具有满足分析要求的数值精度和匹配地形起伏的形态精度。
栅格中间层;尺度适应性;地形分析;数值精度;形态精度
尺度常常被定义为在研究对象或现象时所采用的空间或时间单位,或现象(过程)在空间和时间上所涉及的范围和发生的频率。在现有的地形分析尺度适应性研究成果中,涵盖了DEM地形分析的各个方面:①数据源尺度,如地形图比例尺、遥感影像比例尺等对DEM地形分析的影响;②DEM内插方法对地形分析的影响;③地形分析方法对地形因子和地形特征提取的影响分析。
由于栅格数据在通过离散方式表达连续变化的地形表面过程中存在着尺度依赖性,因此,在栅格中间层的构建过程中,应合理确定栅格中间层的覆盖范围、相应比例尺、栅格单元分辨率等尺度问题,以保证同一级别的栅格中间层在进行叠置、模糊综合评判分析时,不会因为某种尺度不同造成误差甚至导致错误分析结果;另外在进行邻域分析时还会遇到分析尺度大小影响分析结果的情况,也是在栅格中间层构建过程判断算法适应性的关键问题。
1 栅格中间层构建的尺度

图1 栅格中间层构建尺度关系
本文定义了4种栅格中间层的构建尺度,分别是范围尺度、比例尺尺度、分辨率和分析尺度。地形分析尺度是非常复杂的问题,一种统一的尺度不可能适合所有分析对象和分析算法,应该在诸多尺度问题的研究中找到一个相对平衡的统一尺度范围,尽可能满足栅格中间层总体的精度、算法适应性和对各类分析对象的适应性。上述4种栅格中间层构建尺度的结构关系如图1所示。
(1) 范围尺度。栅格中间层数据在构建时以地形表面为基础,是对地形基础因子、地形特征及地形影响因素对专题应用影响程度的数字化表达,本身就具有范围尺度含义。栅格中间层的范围尺度直接决定着其他尺度和栅格中间层的应用目的。
(2) 比例尺尺度。栅格中间层的比例尺尺度体现在地物数据栅格化的矢量数据比例尺,栅格中间层的分辨率尺度与比例尺尺度是相互关联的关系。
(3) 分辨率。在栅格中间层的应用中,各层级中间层将会进行大量的叠置分析、模糊操作,如果分辨率不同,会导致格网计算的不匹配,就会带来大量的内插计算,致使冗余和效率低下。因此,如果能根据分析级别确定满足分析精度要求的统一的格网分辨率,利于栅格中间层的构建和应用。
(4) 分析尺度。分析尺度主要是在计算地形因子和地形特征提取时,分析窗口大小的尺度,分析窗口一般分为3×3、5×5、7×7等矩形分析窗口,不同大小的分析窗口往往跟描述地形表面的曲面次数有关,选择高次曲面相应的分析窗口也应更大,应根据具体算法的适应性确定分析尺度的大小。
2 栅格中间层构建的适宜尺度分析
由于尺度分析的复杂性,在确定栅格中间层构建适宜尺度时,应把握从整体着眼、方便应用,尽量贴近现有标准的原则,在几个尺度之间找到恰当的平衡点,达到在栅格中间层整体构建中现有尺度的矢量数据和栅格数据能直接参与,满足大多数分析任务精度和速度要求的目的,同时不应过于追求细节,执着于某一特定分析对象或某个分析算法的尺度细节要求。
范围尺度、比例尺尺度和分辨率3种尺度之间存在相互关联的关系,因此在尺度适应性研究中,可根据空间分析任务级别及各尺度相互之间的关系分别确定上述3种尺度;分析尺度则应根据具体的栅格数据精度、分析算法适应性确定。
3 栅格中间层的尺度适应性试验
本文分别以3×3、5×5、7×7局部拟合窗口生成切线曲率栅格图和剖面曲率栅格图,DEM数据采用比例尺尺度为1∶5万时25 m×25 m的适宜分辨率,通过曲率计算值的精度、与地形表面形态匹配情况两方面比较验证得出适宜的曲率栅格中间层构建中的分析尺度。
3.1 3×3局部拟合窗口
3×3局部拟合窗口如图2所示。局部曲面拟合计算采用以下公式

(1)
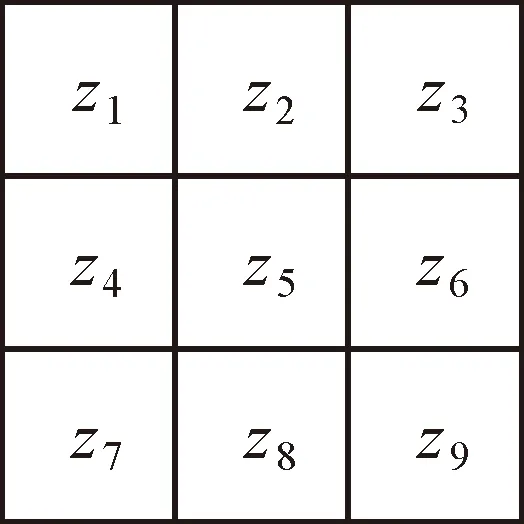
图2 3×3局部拟合窗口
式中

(2)

(3)

(4)

(5)

(6)
移动DEM 3×3局部拟合窗口,可顺序求出除边缘一行和一列以外的所有网格点对应的多项式系数,代入下式

可求出试验区域所有格网点切线曲率的值,将这些切线曲率的值存入新的栅格图层,得到切线曲率栅格层。同样将多项式系数代入下式

可求出试验区域所有格网点剖面曲率的值,将这些剖面曲率的值存入新的栅格图层,得到剖面曲率栅格层。将切线曲率栅格层与DEM栅格晕渲图对比,剖面曲率栅格层与坡度变率栅格层对比,如图3所示(切线曲率栅格层与剖面曲率栅格层采用二值化显示)。

图3 3×3局部拟合窗口曲率计算结果比较验证
从图3可以看出,利用3×3局部拟合窗口生成的切线曲率栅格、剖面曲率栅格与相应的DEM栅格晕渲、坡度变率栅格在形态上相似,但明显的噪声点很多,二值化边界模糊。因此,如果用于地形特征提取,由于大量的噪声点存在,不能很好地反映较大区域的地形形态特征,对于线性地形特征,提取的地形特征线将会界限模糊甚至根本无法体现线性形态,无法用于更高层级的栅格中间层构建。
3.2 5×5局部拟合窗口
5×5局部拟合窗口如图4所示。如果需要不提高拟合多项式次数而增加拟合窗口格网点个数,就要对拟合多项式进行变形,本文利用泰勒级数公式求出拟合多项式fx±nwn=0,1,2,3,…,n的展开式。通过展开式可以得到fx的一阶和二阶差分公式,然后采用该点周围5×5范围网格点的值对局部二次曲面进行最小二乘法拟合,计算曲面上任意一点的曲率。随着格网个数的增加,展开式就会越来越复杂,不利于曲率求解,因此下面推导的5×5和7×7局部拟合窗口曲率计算公式在保证实际应用效果的前提下作了一定量的化简。
局部曲面拟合计算同样采用式(1),其各个参数计算如下
r=-z1+16z2-30z3+16z4-z5-z21+16z22-30z23+16z24-z25/96w2+
-z6+16z7-30z8+16z9-z10-z11+16z12-30z13+16z14-z15-z16+16z17-30z18+16z19-z20/72w2
7
t=-z1+16z6-30z11+16z16-z21-z5+16z10-30z15+16z20-z25/96w2+
-z2+16z7-30z12+16z17-z22-z3+16z8-30z13+16z18-z23-z4+16z9-30z14+16z19-z24/72w2
8
s=z1-8z2+8z4-z5/144w2--z6-8z7+8z9-z10/18w2+z16-8z17+18z19-z20/18w2-
z21-8z22+8z24-z25/144w2
(9)
p=z1+z6+z11+z16+z21-8z2+z7+z12+z17+z22+8z4+z9+z14+z19+z24-z5+z10+z15+z20+z25/60w
(10)
q=z1+z2+z3+z4+z5-8z6+z7+z8+z9+z10+8z16+z17+z18+z19+z20-z21+z22+z23+z24+z25/60w
(11)

图4 5×5局部拟合窗口
移动DEM 5×5局部拟合窗口,可顺序求出除边缘两行和两列点以外的所有网格点对应的多项式系数。与3×3局部拟合窗口相同,将切线曲率栅格层与DEM栅格晕渲对比,剖面曲率栅格层与坡度变率栅格层对比,如图5所示。
从图5可以看出,利用5×5局部拟合窗口生成的切线曲率栅格、剖面曲率栅格与相应的DEM栅格晕渲、坡度变率栅格在形态上相似程度很高,无明显的噪声点,二值化边界清晰。说明用5×5局部拟合窗口计算曲率精度提高,对噪声的压制能力增强。因此,用于地形特征提取,能很好地反映较大区域的地形形态特征,尤其对于线性地形特征,提取的地形特征线将会线形清晰,可以用于更高层级的栅格中间层构建,利用5×5局部拟合窗口计算曲率是一种适宜的分析尺度。

图5 5×5局部拟合窗口曲率计算结果比较验证
3.3 7×7局部拟合窗口
同样,移动DEM7×7局部拟合窗口,可顺序求出除边缘3行和3列点以外的所有网格点对应的多项式系数。与3×3、5×5局部拟合窗口相同,将切线曲率栅格层与DEM栅格晕渲对比,剖面曲率栅格层与坡度变率栅格层对比,如图6所示。从图6可以看出,利用7×7局部拟合窗口生成的切线曲率栅格、剖面曲率栅格噪声点较5×5局部拟合窗口更少,二值化边界更加清晰,说明用7×7局部拟合窗口计算曲率精度更高,对噪声的压制能力进一步增强。但是与相应的DEM栅格晕渲、坡度变率栅格在形态上相似程度下降,拟合曲面与DEM地形曲面之间匹配性减弱,不利于地形特征的提取。

图6 7×7局部拟合窗口曲率计算结果比较验证
因此,太大的局部拟合窗口并不适用于曲率的计算和曲率栅格层的构建,为了使曲率计算精度较高,又同时保持拟合曲面与DEM地形曲面之间的匹配性,根据以上试验情况与结论,推荐使用5×5局部拟合窗口。
4 结束语
本文在曲率栅格中间层适宜分析尺度试验中,得到了与刘学军等对于坡度分析尺度研究相似的试验结果,也印证了坡度分析尺度的可行性,相应可推断在微观地貌因子的栅格层构建中,精度和分析尺度的适应性存在一定的共性。
地物因子的获取主要是通过矢量地物数据栅格化或直接从其他原始数据处理结果中得到,其分析尺度相对简单。地貌因子的获取比较复杂,尤其是微观地貌因子计算涉及曲面微分几何计算,需要考虑算法的计算精度、拟合曲面次数、分析尺度的适宜性等问题,要选择合适的计算方法、拟合曲面和分析窗口大小,使计算结果达到分析任务要求的数值精度,保证在参与数值计算时得到结果的准确性;同时还要使计算结果达到匹配地表起伏的形态精度,保证在参与地形特征提取时得到结果的形态相似性。对于宏观地貌因子的分析尺度,现阶段的研究成果中没有太多可借鉴的结论。另外,由于地形分析任务的级别和类型不同,对分析范围的要求差别也不一样,不能像微观地貌因子一样确定统一的分析尺度,应根据分析任务具体情况确定相应的分析窗口大小。
[1] 赵敏,林行刚,赵乃国,等. 一种DSM模型下飞行障碍物尺度的研究[J]. 清华大学学报(自然科学版),2003,43(9):1249-1250.
[2] 吴勇,汤国安,杨昕.小波派生多尺度DEM的精度分析[J].测绘通报,2007(4):38-45.
[3] 李双成,蔡云龙.地理尺度转换若干问题的初步探讨[J].地理研究,2005,25(1):11-18.
[4] DUNGAN J I,PERRY J N,DALE M R T,et al.A Balanced View of Scale in Spatial Statistical Analysis[J].Ecography,2002(25):626-640.
[5] 李霖,应申.空间尺度基础性问题研究[J]. 武汉大学学报(信息科学版),2005,30(3):200-202.[6] 汤国安,刘学军,房亮,等.DEM 及数字地形分析中尺度问题研究综述[J]. 武汉大学学报(信息科学版),2006,31(12):1060-1065.
[7] 刘学军,卢华兴,仁政,等.论DEM地形分析中的尺度问题[J].地理研究,2007,26(3):433-442.
[8] FULLER I C,LARGE A R G,CHARLTON M E,et al.Reachscale Sediment Transfers:An Evaluation of Two Morphological Budgeting Approaches[J].Earth Surface Processes and Landforms,2003,28(8):889-903.
[9] 张景雄.空间信息的尺度、不确定性与融合[M].武汉:武汉大学出版社,2008:8-14.
[10] 申成磊,马劲松.栅格尺度对DEM分析中地形因子的影响[J].现代测绘,2007,30(6):3-6.
[11] ANDR S A,FRDRIC C,YANN G,et al.Interpolation of Digital Elevation Models Using AMLE and Related Methods[J].IEEE Transactions on Geoscience and Remote Sensing,2002,40(2):314-325.
[12] 刘学军,龚健雅,周启鸣,等.基于DEM坡度坡向算法精度的分析研究[J].测绘学报,2004,33(3):258-263.
[13] WARREN S D,HOHMANN M G,AUERSWALD K,et al.An Evaluation of Methods to Determine Slope Using Digital Elevation Data[J].Catena,2004(58):215-233.
[14] 刘学军,张平,朱莹.DEM 坡度计算的适宜窗口分析[J].测绘学报,2009,38(3):264-270.
[15] MAMILLAN R A,SHARY P A.Landfoms and Landform Elements in Geomorphometry[J].Developments in Soil Science,2009(33):233-234.
[16] 秦承志,呼雪梅.栅格数字地形分析中的尺度问题研究方法[J].地理研究,2014,33(2):270-283.
ScaleAdaptabilityofRasterIntermediateLayerinTerrainAnalysis
ZHANG Lichao1,ZHAO Peng2,ZHANG Hechao3
(1. Information Center of Henan Administration of Surveying, Mapping and Geoinformation, Zhengzhou 450003,China; 2. Institute of Geospatial Information, Information Engineering University, Zhengzhou 450052,China; 3. Keyuan Surveying and Mapping Center of Henan Province, Zhengzhou 450003,China)
Raster intermediate layer is fundamental and reusable raster layer for terrain analysis created by the DEM, DSM, vector data, which is obtained through a series of raster calculation. The scale adaptability of raster intermediate layer is studied. The range, scale, resolution, analysis are defined. The principle of range, scale, resolution are determined. Particularly, the paper takes the experiment of scale adaptability of the tangent, curvature raster intermediate layer aiming at the analysis scale, and puts forward the adaptive algorithm and analysis scale. The result shows that raster intermediate layer of terrain foundation factors created from this solution meets the need of numerical precision and morphology precision for terrain analysis.
raster intermediate layer;scale adaptability;terrain analysis;numerical precision;morphology precision
P208
A
0494-0911(2017)01-0130-04
张立朝,赵鹏,张合朝.地形分析中栅格中间层构建的尺度适应性[J].测绘通报,2017(1):130-133.
10.13474/j.cnki.11-2246.2017.0029.
2016-03-03
国家自然科学基金(41201390);矿山空间信息技术国家测绘地理信息局重点实验室开放基金(KLM201411);信息工程大学地理空间信息学院自立科研课题(Y1106)
张立朝(1981—),男,工程师,主要从事地理国情监测及地理信息服务。E-mail:13838205603@163.com
