GNSS空间信号法时差监测方法与结果分析

章洁君，陈俊平,2，张益泽,3

(1. 中国科学院上海天文台，上海 200030； 2. 中国科学院上海天文台上海市空间导航与定位技术重点 实验室，上海 200030； 3. 同济大学测绘与地理信息学院，上海 200092)

GNSS空间信号法时差监测方法与结果分析

章洁君1，陈俊平1,2，张益泽1,3

(1. 中国科学院上海天文台，上海 200030； 2. 中国科学院上海天文台上海市空间导航与定位技术重点 实验室，上海 200030； 3. 同济大学测绘与地理信息学院，上海 200092)

比较了3种基于GNSS空间信号进行时差监测的方法，其中，单站精密单点定位(PPP)时差监测法依赖于卫星轨道和钟差的精度，高精度PPP一般采用事后处理的方法；网解时差监测法受卫星轨道误差的影响较小，且不受卫星钟差误差的影响，因此能够用于高精度时差实时监测。为分析不同方法时差监测的差异，在距离不同的时间实验室之间进行了时差试验，试验中将外接相同原子钟的两个测站的时差用于评定时差监测的精度，而相距2000 km的测站用于验证高精度实时时差监测的精度。结果表明：①实时网解与事后PPP时差监测的精度相当，达到了0.16 ns；②采用PPP方法，是否固定站坐标时差结果差异的RMS为0.04 ns；③采用实时网解的方法，对于相隔数千千米的测站实时时差监测，其与PPP后处理结果的差异约为0.14 ns。

时差监测；空间信号法；实时网解；PPP

传统的时差监测方法主要有卫星双向时间频率传递法(TWSTFT)和卫星共视法等方法，其中，TWSTFT利用专用的时间同步链路，系统复杂且经济成本较高，卫星共视方法是基于对GNSS卫星的伪距观测值，其精度较差[1-2]。结合GNSS数据处理技术的发展，近年来基于导航系统空间信号的时差监测技术得到了较快发展，提高了时差监测的实时性及监测精度[3-5]。空间信号法时差监测主要有两种方法：PPP技术和多站网解技术[6]。单站精密单点定位技术在求取测站坐标的同时求取测站钟差参数；它要求固定卫星轨道和钟差，因此高精度的PPP时差测量一般采用后处理的方式[7-8]。多站网解技术固定了参考站的坐标及钟差参数，求解其他站的相对钟差，同时卫星钟差也作为参数进行求解；网解技术中卫星轨道误差对网解数据处理影响较小，并且其影响最大的径向部分会被卫星钟差参数吸收，因此网解技术能够实现高精度的实时时差监测[9]。

本文拟比较分析基于PPP及网解技术时差监测的模型和数据处理方法，设计时间实验室的时差监测试验，通过时差参数的精度及稳定性情况评定这两种方法时差监测的精度，验证基于网解技术长距离实时时差监测的可行性。

1 GNSS空间信号法时差监测原理

GNSS空间信号法时差监测方法一般采用非差无电离层组合模型，其伪距、相位观测方程如下

(1)

时差解算中，卫星位置一般可采用精密轨道进行固定，测站坐标可以作为参数估计或固定为精确已知值；接收机钟差、模糊度等参数一般作为参数估计。采用PPP进行时差监测需要固定卫星的钟差，因此这种方法在实时处理中精度受到实时钟差精度的约束，基于广播星历的钟差精度能够达到大约2～5 ns[11]。网解技术则将卫星钟差也作为待求参数，因此其精度不受输入卫星钟差精度的影响，能够实现高精度的实时解算[12]。网解技术中测站和卫星钟差参数的同时解算存在秩亏，需要定义一个钟差基准，从而解算的钟差参数都是相对该基准的相对钟差[13]。

以上的数据处理都是基于相位观测，单站的相位处理由于模糊度无法固定，一般存在一定的收敛时间。基于网解的相位处理可进行双差模糊度固定，因此其实时收敛的时间更短。

获取的钟差参数包含了接收机设备时延，对于定时接收机该时延值可在实验室进行高精度标定。对于外接时频信号T(A)的GNSS接收机A，以上钟差结果扣除设备时延后，得到的测站钟差为外接时间信号T(A)与卫星系统时间GNSST之差[14]

δA=GNSST-T(A)

(2)

不同接收机钟差作差得到外接时频信号的差异，即为时差测量值

ΔT=δA-δB

=GNSST-T(A)-GNSST-T(B)

=T(B)-T(A)

(3)

2 计算结果及分析

对GNSS信号法时差监测方法进行测试，设计了验证试验。试验中在成都某时频实验室实验场架设5台GNSS接收机，其中1台接收机REF连接了该实验室基准时频信号，另外4台(A、B、C、D)是为了此次测试在其附近临时架设的，此外将距离测试场地约为2000 km的测站E也加入处理分析。以上测站中A、B站外接至同一台原子钟。试验测量了2015年第228和229年积日的数据，并分别使用事后PPP和实时网解技术获取测站钟差。实时网解中以实验室原子钟作为基准，求取其他测站相对于REF站的时差。

2.1 时差结果分析

由于PPP时差测量需要收敛，因此结果比较中不包含刚开始观测的1小时数据。由于篇幅限制，仅图1给出网解技术所得的测站钟差(扣除了线性项)的结果，图2为各测站相对于A站的时差计算值，表1在图1的基础上统计了拟合残差，作为时差测量的精度。

图1 网解时差监测测站钟差序列

分析图1和图2可知，测站钟差解算两天的吻合度较好。C站未连接氢原子钟，其本身噪声较大，其他3个测站的钟差值均表现出较小的噪声。从表1可以看到，对于外接了原子钟的测站，3种方法的测站钟差精度都在0.2 ns以内，平均为0.16 ns。对于A与B站的时差，其频率差异为-1.28×10-15，由于A、B外接了相同的时频信号，因此该频率的差异主要反映了接收机的噪声及性能。而C站3种技术求得的测站钟差RMS均大于0.3 ns，由于未接时频信号，其时差噪声较大。

表1 3种时差监测方法测站钟差结果RMS值比较 ns

图2 网解测站时差序列

2.2 实时网解与PPP事后处理时差结果的比较

将网解方法与事后PPP方法获取的时差测量值作比较，如图3所示。从图3中可看到，网解结果与PPP结果吻合较好，其差异的RMS为0.04 ns。PPP处理中对于坐标已知的测站可以进行坐标的固定，将其与常规PPP的结果进行比较，图4列出了不同测站这两种方法的差异，其结果基本吻合，差值的RMS约为0.04 ns。因此，是否固定测站坐标对解算结果影响不大。

网解方法把卫星钟差与测站钟差一起作为参数估计，可实现长距离实时的时差观测。图5比较了距离达2000 km的E站与A站的实时时差测量值与PPP事后处理的结果。两者结果基本吻合，且两天的结果一致，差值的RMS均值为0.14 ns。因此可以认为，对于长距离的测站，实时网解可与事后PPP解算精度一致。

2.3 实时网解与PPP事后处理时差频率稳定度的比较

在时间领域中，使用Allan方差来评估利用GNSS方法得到的产品的时域稳定度，在实际测量中，Allan方差是描述随机噪声时域统计特性的通用标准[15]。其公式为

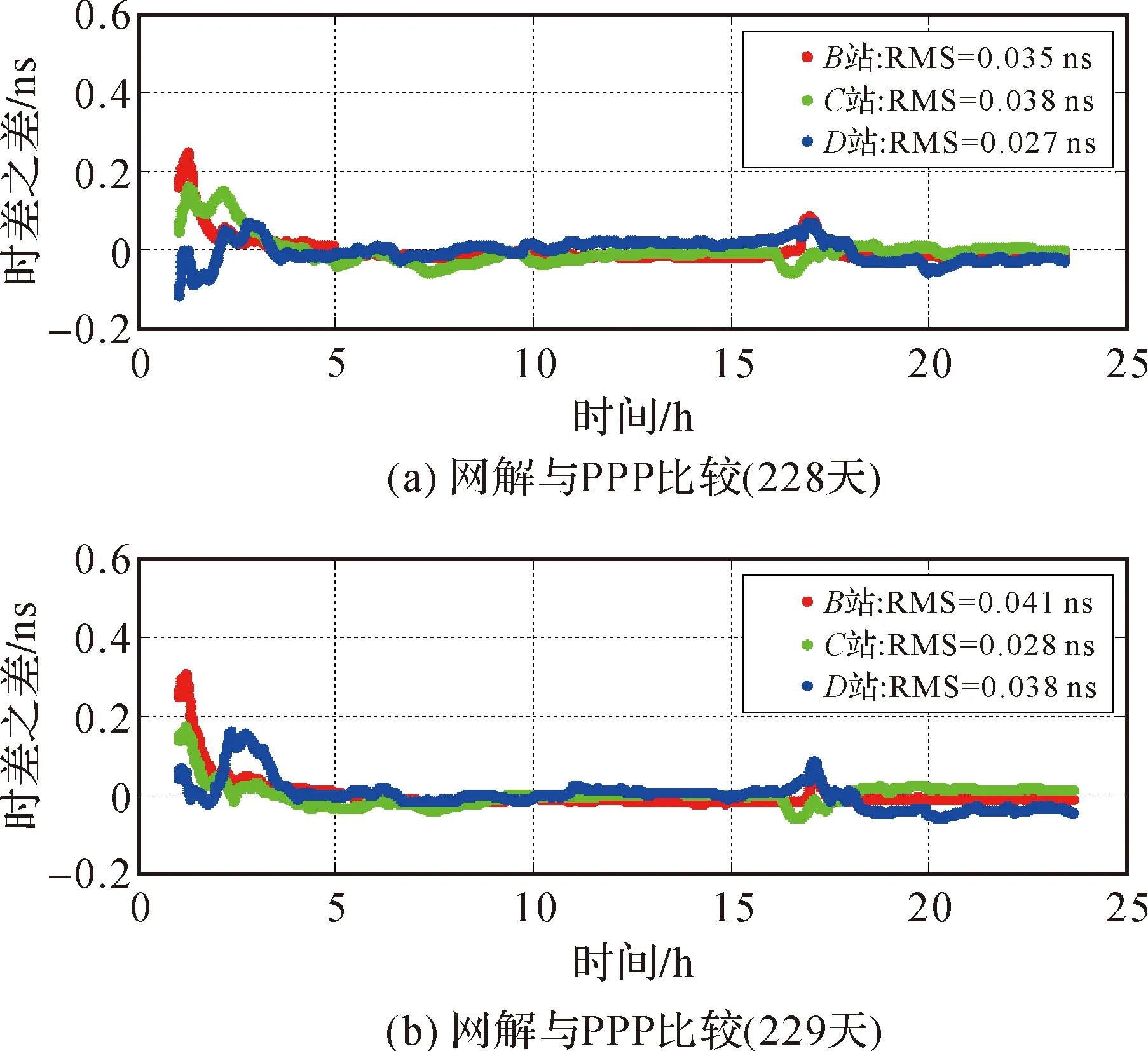
图3 网解时差监测与PPP时差监测的比较

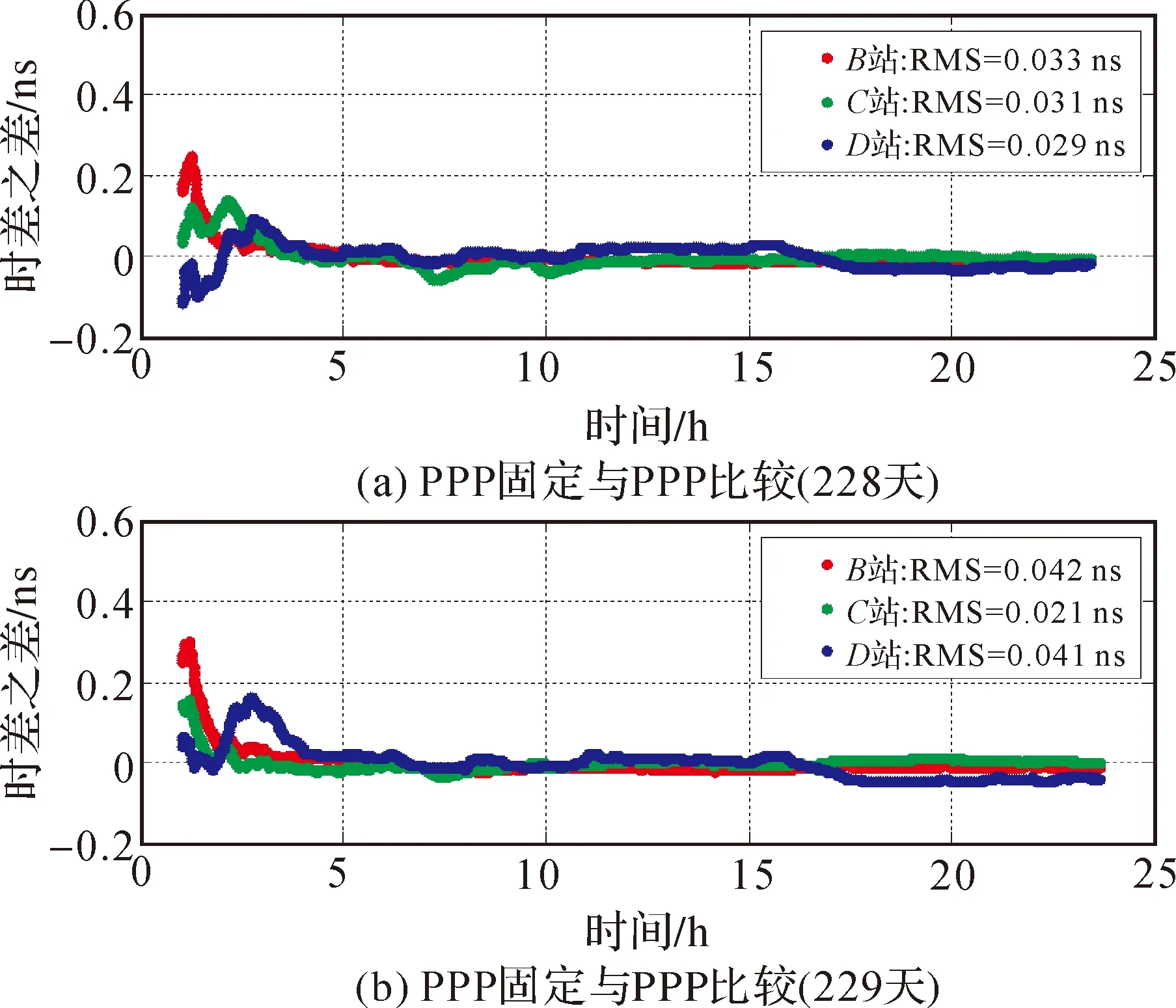
图4 PPP是否固定站坐标对时差监测的影响

(4)

式中，xi为历元i的观测值；N为观测序列的长度；τ为采样间隔，τ=nτ0，τ0为原始观测序列采样间隔；n为正整数(1≤n≤N)。本文中，xi是历元i的钟差解，N为钟差解序列样本总数(即历元数)，τ0为观测值采样间隔30 s。

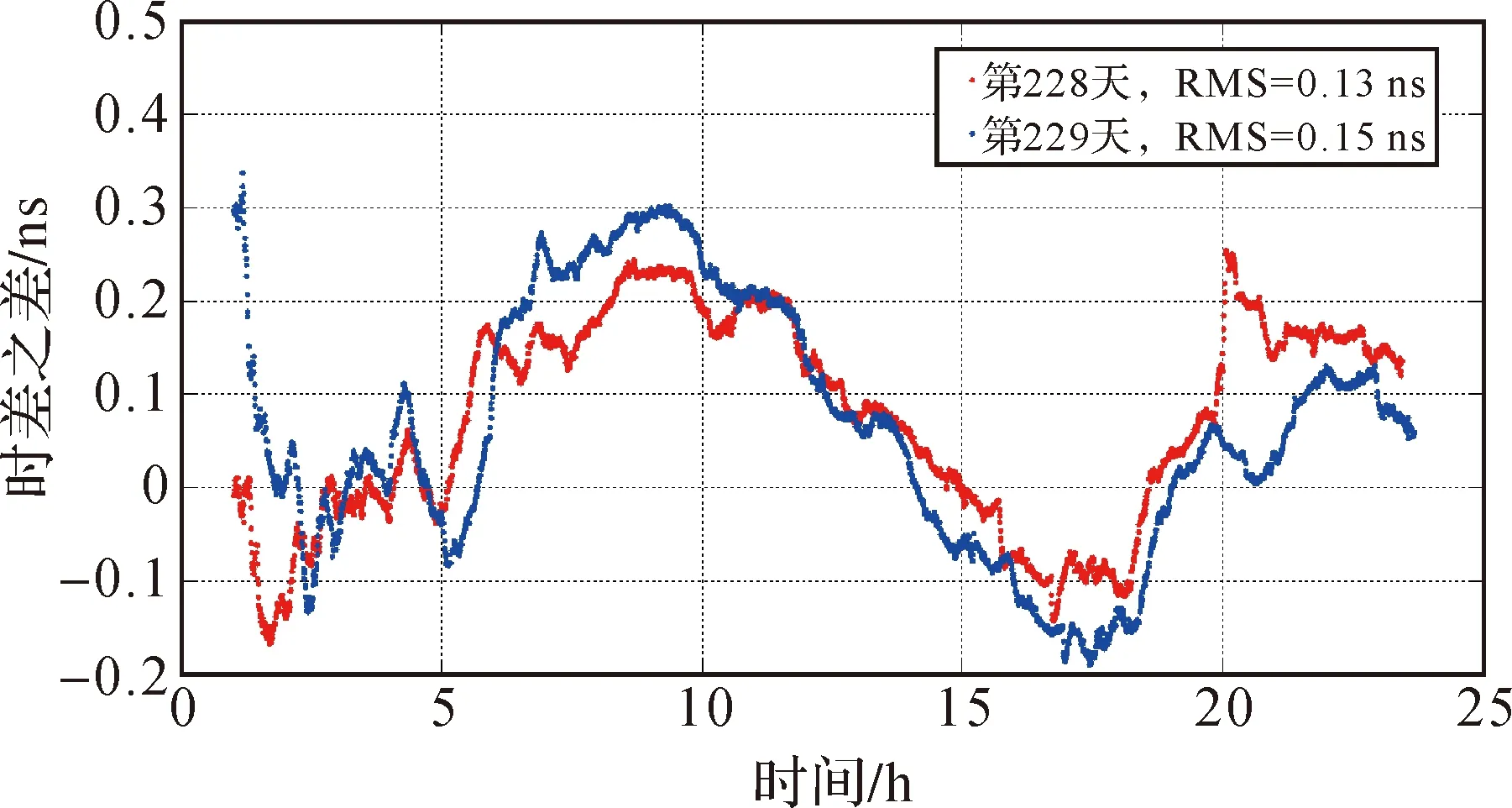
图5 长距离实时网解与PPP事后处理时差结果的比较

基于以上数据处理的结果，分析了不同采样率下的Allan方差，如图6所示。

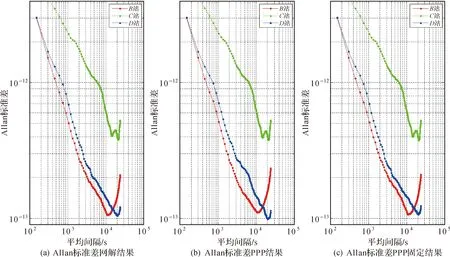
图6 Allan方差时差序列

结合图6可知，3种方法计算得到的Allan方差统计结果相当，说明这3种时差解算方法的频率稳定度一致。其中10 000 s间隔的频率稳定度在1×10-13～1.5×10-13左右。

3 结 论

针对以上关于3种时差监测方法的研究和验证，得出以下结论：

(1) PPP、PPP固定和实时网解时差监测的结果均能够达到优于0.2 ns的精度，频率万秒的稳定度为1×10-13～1.5×10-13。

(2) 实时网解与PPP事后处理时差监测的精度相当，都优于0.2 ns。距离达2000 km的实时网解时差测量精度与PPP差异为0.14 ns。

(3) 采用PPP方法，是否固定站坐标造成时差监测结果差异的RMS为0.04 ns。

[1] 江志恒. GPS全视法时间传递回顾与展望[J]. 宇航计测技术,2007(S1):53-71.

[2] SENIOR K,KOPPANG P,RAY J.Developing an IGSTime Scale[J].IEEE Transactions on UltrasonicFerroelectric Frequency Control,2003,50(6):585-593.

[3] KOUBA J,SPRINGER T.New IGS Station and Satellite Clock Combination[J].GPS Solutions,2001，4(4):31-36.

[4] SENIOR K.New IGS Timescaleamp;New UT1/LODSeries[C]∥Analysis Center Workshop.Florida：[s.n.]，2008.

[5] 周钰，熊耀恒.利用卫星进行双向时间传递[J]. 天文研究与技术.国家天文台台刊,2006,3(1):28-34.

[6] ORGIAZZI D,TAVELLA P,LAHAYE F.Experimental Assessment of the Time Transfer Capability of Precise Point Positioning(PPP)[C]∥IEEE International Frequency Control Symposiumand amp; Exposition.Vancouver,BC,Canada：IEEE,2005.

[7] 杨文辉，黄新宝，罗锐.卫星导航时间传递性能的分析与比较[J].现代导航,2013(1):14-18.

[8] HEERING T.Impact of Absolute Phase Center Models on GPS Reference Frames[C]∥European Geosciences Union General Assembly,Massachusetts.Cambridge:[s.n.],2007.

[9] 李浩军,王解先,陈俊平，等. 基于GNSS网络的实时精密单点定位及精度分析[J]. 地球物理学报,2010,53(6)：1302-1307.

[10] 刘经南,叶世榕. GPS非差相位精密单点定位技术探讨[J]. 武汉大学学报(信息科学版),2002,27(3):234-240.

[11] 张小红,程世来,李星星,等.单站GPS载波平滑伪距精密授时研究[J]. 武汉大学学报(信息科学版),2009,34(4):463-465.

[12] 刘晓刚,吴晓平,张传定. 卫星双向共视法时间比对计算模型及其精度评估[J]. 测绘学报,2009,38(5):415-421.

[13] 陈俊平,张益泽,谢益炳,等. 超大观测网络及多GNSS系统的快速数据处理[J]. 武汉大学学报(信息科学版),2014,39(3):253-257.

[14] 辜声峰. 多频GNSS非差非组合精密数据处理理论及其应用[D].武汉：武汉大学,2013.

[15] 张小红,蔡诗响,李星星,等.利用GPS精密单点定位进行时间传递精度分析[J]. 武汉大学学报(信息科学版),2010,35(3):274-278.

ResearchandResultsAnalysisofMethodsofGNSSSpatialSignalTimeMonitoring

ZHANG Jiejun1,CHEN Junping1,2,ZHANG Yize1,3

(1. Shanghai Astronomical Observatory,Chinese Academy of Sciences, Shanghai 200030, China; 2. Shanghai Key Laboratory of Space Navigation and Positioning Technology,ShanghaiAstronomical Observatory, Chinese Academy of Sciences, Shanghai 200030, China; 3. College of Surveying and Geo-informatics, Tongji University, Shanghai 200092, China)

Methods using GNSS signal in space to monitor time offset among timing stations are dicussed. Three methods namely the traditional PPP, PPP with fixed station coordinates and the real-time network solutions are compared. To validate and assess the performance of SIS time offset monitoring, data of 5 GNSS stations with different configurations are analyzed.Results show that: (1)Precision of real time network solutions is 0.16 ns, which is at the same level of post-processed PPP.(2)Station coordinates estimation has impact on the determination of station clocks，which is about 0.04 ns. (3) Precision of time transfer for stations depart 2000 km could reach 0.14 ns in the real-time network solution.

time monitoring； spatial signal; real-time network solution;PPP

P224

A

0494-0911(2017)01-0026-04

章洁君，陈俊平，张益泽.GNSS空间信号法时差监测方法与结果分析[J].测绘通报，2017(1)：26-29.

10.13474/j.cnki.11-2246.2017.0006.

2016-05-05；

2016-05-27

中科院百人计划；国家863计划(2013AA122402；2014AA123102)；国家自然科学基金(11273046)

章洁君(1991—)，女，硕士，研究方向为GNSS精密数据处理。E-mail：jjzhang@shao.ac.cn