某工程车铰接装置优化设计

王 娟

（山西轻工职业技术学院， 山西 太原 030013）

试（实）验研究

某工程车铰接装置优化设计

王 娟

（山西轻工职业技术学院， 山西 太原 030013）

针对某铰接式工程车交接装置处容易损坏、断裂的现象，建立其满载时的多刚体转向虚拟样机模型并进行仿真分析，发现该车的单自由度交接装置在车辆通过矩形坑路面时，前机架与交接装置销轴接触处存在应力过度集中现象，是交接装置损坏的主要原因。将单自由度交接装置设计改进为双自由度交接装置，并建模进行仿真分析，验证了设计后车辆在通过障碍路面时，前后交接装置及车体力学性能明显优于单自由度情况，材料安全系数及可靠性大大增强，可以避免交接装置及车体的损坏现象。

铰接装置 优化设计 双自由度 仿真

由于铰接式工程车辆使用的路面条件恶劣，在使用过程中，其交接装置及其周围易出现裂纹、断裂等不同程度的损坏现象。本文以某型号铰接式工程车为研究对象，建立其虚拟样机模型，仿真车辆通过不同路况时的受力情况，分析交接装置损坏原因，并通过对其进行设计改进，并验证改进后的交接装置能满足恶劣路面下的使用要求，避免上述问题发生。

1 交接装置损坏原因分析

该铰接式工程车外形尺寸8 100 mm×2 100 mm×2 010mm，自身质量为10 t，额定载重质量为8 t，主要组成部件包括：前后机架、柴油机系统、传动系统以及附属系统等。本文利用三维设计软件Solidworks，按照车辆的实际参数建立整车三维模型，导入动力学仿真软件ADAMS中，设置相应的运动副和约束[3]，得到该工程车整车模型如图1所示。

图1 铰接式工程车整车虚拟模型

本文选用三角凸起、矩形坑和搓板等三种比较经典路况对该车虚拟样机模型以相同的车速分别做直线行驶和转弯行驶仿真计算[4-5]，得到车辆交接装置处受力峰值及垂向受力峰值如表1所示。

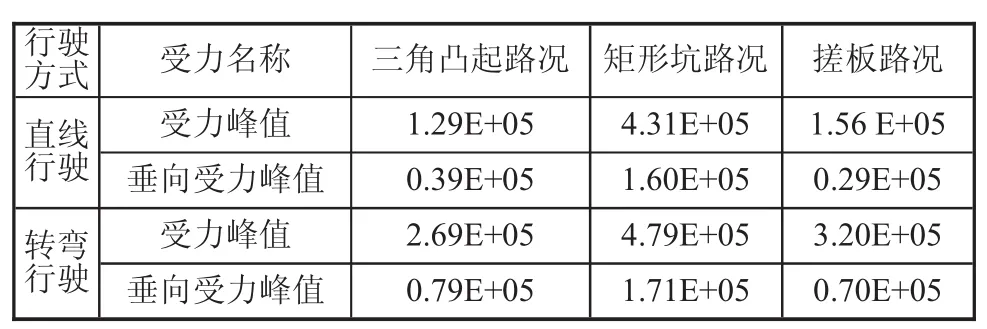
表1 车辆三种路况下行驶交接装置处受力峰值及垂向受力峰值

分析表1仿真数据可知，该工程车以相同的速度行驶，交接装置受力在转弯行驶时较直线行驶时大，矩形坑路况行驶时交接装置总体受力较大。因此，本文利用有限元软件对该车的交接装置受力分析是以该工程车满载转弯驶过矩形坑路时所受动态力为加载条件的。

利用车辆实际参数及车辆转向通过矩形坑路面时的动态仿真所得动态力，对如图2所示的该车交接装置有限元模型并施加载荷和约束，仿真计算得到机架铰接处的动态应力值和应力云图，分别如下页图3和4所示。

图2 交接装置有限元模型

图3 前机架与交接装置销轴接触处应力变化曲线

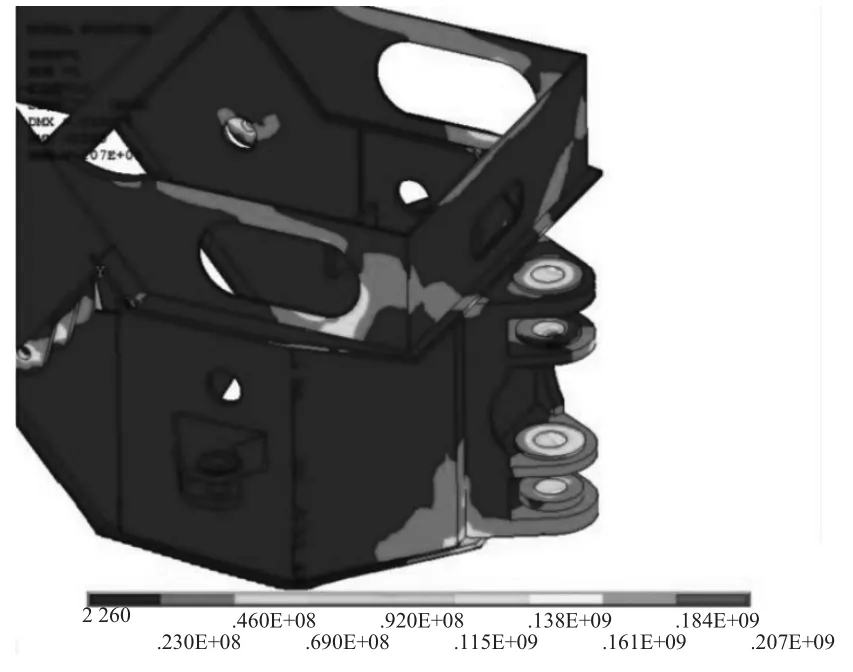
图4 前机架受力最大时刻应力云图

由图3可知，仿真在第9 s时应力值为216 MPa，达到最大，材料屈服极限345MPa，此时材料安全系数为1.59，非常接近最低值1.5，安全系数低。且由图4可以看出，仿真第9 s时，前机架与销轴接触处出明显的现应力集中点。

上述分析表明，该单自由度铰接式工程车在矩形坑路面转弯行驶时，在前机架与交接装置销轴接触处存在局部应力过度集中现象，会导致连接部损坏或出现裂纹，是交接装置损坏的主要原因。

2 交接装置优化设计及合理性验证

为解决工程车交接装置易损坏的问题，本文将车辆单自由度交接装置改进为双自由度交接装置，增加前后车架横向摆动自由度[6]。

综合比较多种双自由度铰接形式[7-8]，本文设计选用了如图5所示的双自由度交接装置，由前铰接架1、销轴2、后铰接架3、滚珠轴承4、定位座5、卡紧螺母6、端盖7、轴承座8以及润滑油口9组成。前铰接架1与后铰接架3通过销轴2实现一个自由度。后铰接架3与定位座5通过滚动轴承4及其他附件实现了第二个自由度。该双自由度交接装置实现了前后机架的相互独立摆动，且不需要车架的大范围改动。本文建立双自由度工程车整车虚拟模型如图6所示。

图5 双自由度交接装置结构示意图

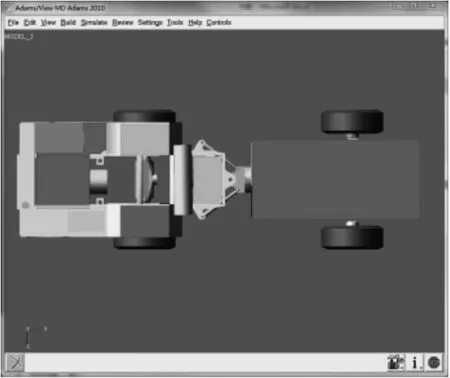
图6 双自由度工程车整车虚拟模型

由于上述分析得知该铰接式胶轮车分别通过三种路况时，车辆转弯状态下的铰接处受力均明显大于之行状态时的受力。因此，本文对双自由度铰接时胶轮车进行了转弯状态下通过三种路面的仿真分析，仿真结果如表2所示。

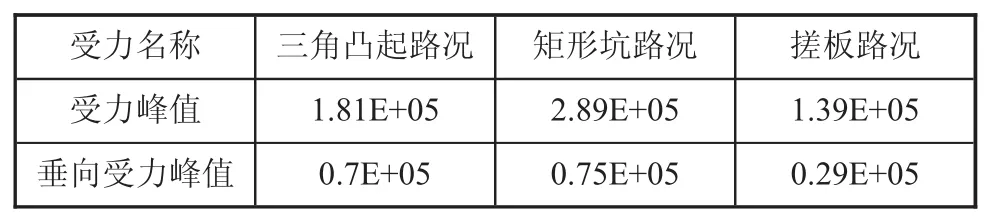
表2 双自由度铰接胶轮车转弯通过三种路况时铰接处受力情况 Pa

对比表1和表2可知，双自由度铰接式胶轮车在通过不同的路面工况时铰接处受力均明显小于单自由度铰接式胶轮车。车辆在越过路障时，前后机架在交接装置产生的扭矩减小，降低了对交接装置的损坏程度，更有利于车辆的稳定、安全行驶。

由表2可知，在矩形坑路况下车辆前后机架铰接处受力相对较大一些。所以同样选取矩形坑路面受力情况作为加载条件，双自由度交接装置进行有限元分析。双自由度交接装置有限元模型如图7所示。对此模型进行仿真计算，得到双自由度交接装置应力曲线及应力分布云图，如图9—12所示。

由图8的交接装置与后车架连接处应力变化曲线可知，最大应力值为160MPa，材料屈服极限345 MPa，此时材料安全系数为2.16，安全系数高。由图10的交接装置与前车架连接处应力变化曲线显示最大应力值为101MPa（此时材料安全系数为3.4），远小于图3中的最大应力值216，安全系数很高。在图9的交接装置与后车架连接处应力分布云图和图11的交接装置与前车架连接处应力分布云图中均无明显的应力集中现象。分析结果表明，改进设计后的双自由度铰接式工程车在通过障碍路面时，前后交接装置及车体力学性能明显优于单自由度情况，材料安全系数及可靠性大大增强，可以避免交接装置及车体的损坏现象。

图7 双自由度交接装置有限元模型

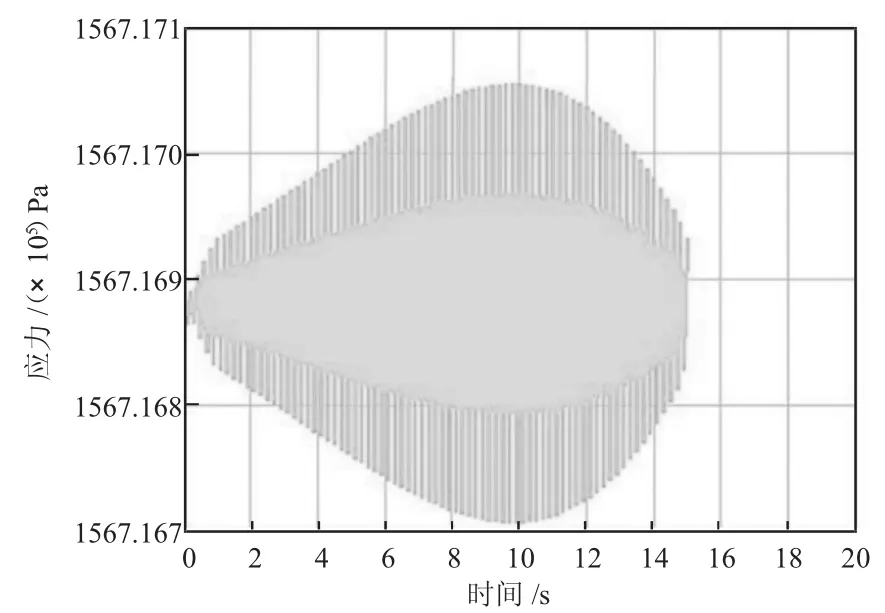
图8 交接装置与后车架连接处应力变化曲线

图9 交接装置与后车架连接处应力分布云图

图10 交接装置与前车架连接处应力变化曲线

图11 交接装置与前车架连接处应力分布云图

3 结语

单自由度铰接式工程车在通过恶劣路面时，在前机架与交接装置销轴接触处存在局部应力过度集中现象，会导致连接部损坏或出现裂纹，是交接装置损坏的主要原因。本文改进设计后的双自由度铰接式工程车在通过障碍路面时，前后交接装置及车体力学性能明显优于单自由度情况，材料安全系数及可靠性大大增强，可以避免交接装置及车体的损坏现象。双自由度铰接式工程车投放市场后，再没有出现过交接装置损坏问题，受到一致肯定。

[1] 申焱华，李艳红，金纯.电驱动铰接式工程车辆操纵稳定性控制分析[J].农业工程学报，2013，29（12）：71-78.

[2] 高德峰，马志国，张洛明.基于ADAMS电驱动铰接车行驶稳定性建模分析[J].机械设计与制造，2016（12）：57-60.

[3] Iida M,Nakashima H,Tomiyama H.Small-radius turning performance of an articulated vehicle by direct yaw moment control[J].Computersand Electronics in Agriculture，2011，76：277-283.

[4] 范珍珍.基于油缸铰接点位置铰接车转向机构优化设计[J].机械设计与制造，2016（10）：110-113；117.

[5] 王起梁，曾京.铰接式集装箱平车动力学建模与仿真[J].铁道车辆，2006（7）：4-8；45.

[6] 鲁力群，赵静，石博强.铰接式自卸车铰接系统结构性能分析及试验研究[J].煤炭学报，2010，35（2）：324-328.

[7] 刘立，刘雪伟，孟宇.基于OGRE的铰接式地下矿车驾驶模拟系统[J].农业机械学报，2013，44（8）：38-44；68.

[8] 李春英，师东波，钱振朋.基于遗传算法铰接式车辆油缸铰接点位置的优化研究[J].机械设计与制造，2017（1）：94-96.

Optim ization Design of Articulated Device for An Engineering Vehicle

W ang Juan
（Shanxi Vocational and Technical College of Light Industry,Taiyuan Shanxi030013）

Aiming at the phenomenon that the hingemechanism of an engineering vehicle is easy to be damaged and broken,the multi-rigid-body-to-virtual model is designed and simulated.It is found that the singledegree-of-freedom articulation mechanism of the vehicle,when passing through the rectangular pavement,there is excessive stress concentration in the contactbetween the front frame and the hinge plate pin,which is themain reason for the damage of the hingemechanism.The two-degree-of-freedom hingemechanism is designed for the vehicle.The simulation results show that themechanical properties of the hinged device and the vehicle body are better than those of the single degree of freedom.The safety factor and reliability of the vehicle are greatly enhanced to avoid the hinge device and the body of the damage.

articulated device；optimal design；double degree of freedom；simulation

TH6

A

1672-1152（2017）05-0031-03

10.16525/j.cnki.cn14-1167/tf.2017.05.12

2017-08-17

王娟（1988—），女，助教，硕士，毕业于太原理工大学，现从事机械工程专业的教学与科研工作。

（编辑：苗运平）