The width directions of a strictly reduced convex body in En

WU Hongjian,GUO Qi

（School of Mathematics and Physics，SUST，Suzhou 215009，China）

The width directions of a strictly reduced convex body in En

WU Hongjian,GUO Qi*

（School of Mathematics and Physics，SUST，Suzhou 215009，China）

A convex body R in Euclidean space Enis called reduced if the minimal width Δ（K） of every convex body K⊆R properly is smaller than Δ（R）.It is known that each strictly reduced convex body in E2is of constant width.This paper discusses the width direction of a strictly reduced convex body in En.

strictly reduced convex body；width direction;normal cone；extreme ray

The concept of reduced bodies,as a “dual” concept of complete bodies,was introduced by Heil in[1].A convex body,i.e.a compact convex set with non-empty interior,in the n-dimensional Euclidean space Enis called to be reduced if it does not properly contain a convex body of the same width.It is easy to know that convex bodies of constant width （see below for the definition） are naturally reduced.It is also known that there are indeed reduced bodies other than the constant ones[2]even if it was confirmed that each strictly convex reduced body in E2is of constant width[2-3]and that each smooth reduced convex body in Enis of constant width（the second conclusion holds in the Minkowski space Mnas well[4-7]）.However,there are too few examples of non-trivial reduced convex bodies since there seems no general method to construct reduced convex bodies.Thus,it is of obvious significance to find the characteristics of reduced convex bodies.

The width direction（see below for the definition） of a reduced body is one of the main topics in studying the characters of reduced convex bodies.Along this stream,Lassak gave a necessary and suficient condition in E2for a direction to be width direction[2，7].Dekster discussed in Enthe width direction of a reduced body at its regular points[8].

The aim of this paper is to extend Lassak's results about the width direction of a reduced body in E2to strictly convex reduced bodies in En.

1 Preliminaries

In this paper,we will work in Enwith the usual scalar product〈·，·〉and the induced Euclidean norm｜｜·｜.For x，y∈En,we write

for the closed segment with endpoints x，y.

Let C be a convex body in En.

A point x∈bdC,the bondary of C,is said to be a regular point if the support hyperplane of C at x is unique,a singular point if otherwise.

A vector s∈Enis called a direction tangent to C at x∈C if there exist a sequence{xi}⊂C and a sequence{ti}⊂E such that

A sequence{xi}as above is called a tangent-direction-attaining sequence of s（an s-attaining sequence for brevity）.The set of all such tangent directions is called the tangent cone to C at x∈C,denoted by TC（x）.

A vector u∈Enis said to be normal to C at x∈C if

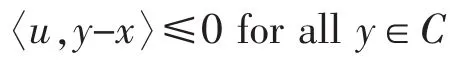
The set of all such directions is called the normal cone to C at x,denoted by NC（x）.It is easy to see that x∈bdC is regular iff NC（x） is a ray starting from the origin.It is known that both TC（x） and NC（x） are closed convex cones and dual to each other.

The support function h（C，·） of C is defined by

For non-zero u∈En,the set

is called the support hyperplane of C with outer normal vector u.The number

is called the width of C in the direction u,where Sn－1is the unit sphere of En.If w（C，u） is independent of u,then C is called a convex body of constant width.It is clear that w（C，u）=w（C，－u）.The minimal width

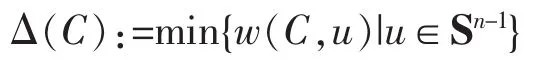
is called the width of C.A direction u∈Sn－1satisfying w（C，u）=Δ（C） is called a width direction of C.For convenience,we call also any non zero vector u a width direction if u/||u||is a width direction.Thus,u is a width direction iff-u is a width direction for all u∈En{0}and that u is a width direction iff λu is a width direction for any λ≠0.

A face of a convex set D is a convex subset F⊂D such that x，y∈D and（1/2）（x+y）∈F imply x，y∈F.An extreme ray of a convex set D is a ray that is a face of D.By extrD we denote the union of extreme rays of D.extrD may be empty in general,however,if D=K is a non-trivial convex cone,i.e.K is line-free and nonzero cone（as in[9],we assume that the origin o is the vertex of a cone all the time）,then extrK≠Ø.Furthermore,L is an extreme ray of K iff there is a support hyperplane H：={x∈En|〈s，x〉=0}of K,where 0≠s∈En,such that L=K∩H[9-10].

In terms of extreme rays of normal cones,we may reformulate Lassak's and Dekster's results as follows.

Theorem A[7]Let C∈E2be a reduced convex body.Then u∈S1is a width direction of C iff there is x∈bdC such that u or-u∈extrNC（x）.

Theorem B[8]Let C∈Enbe a reduced convex body.If x∈bdC is regular,i.e.NC（x）=extrNC（x） is a ray,then each u∈NC（x）{0}is a width direction of C.

In this paper,we study the width direction of strictly convex reduced bodies in En.Concretely,we will show the following theorem.

Theorem CLet R⊂Enbe a strictly convex reduced body,p∈bdR and nonzero l∈extrNR（p）,then w（R，l）=Δ（R）,i.e.l is a width direction of R.

We recall the following propositions from[8]for the later uses.

Proposition 1[8]Let Ci，C be convex bodies in Enand ui，u∈Sn－1，i=1，2，….If Ci→C w.r.t.the Hausdorff metric and ui→u,then w（Ci，ui）→w（C，u）.

Proposition 2[8]If w（C，u）=Δ（C）,then among the chords parallel to u of C there is one with length Δ（C）.Such a chord is unique if one of the two supporting hyperplanes orthogonal to u has only one common point with C.That point is an end of the chord.

2 Some properties of the tangent cones and the normal cones

In this section,we discuss some properties of the tangent cones and the normal cones of convex bodies.More precisely,we present some kind of continuity of the tangent cones or the normal cones w.r.t.the points and/or the convex bodies,which will be used in the proof of Theorem C and are of significance themselves.

The first result concerns some kind of continuity of the normal cones.

Proposition 3Let Ci，C be convex bodies in Ensuch that Ci→C w.r.t.the Hausdorff metric,pi∈Ciand p∈C with pi→p,and li∈NCi（pi）,i=1，2，….If li→l as i→∞,then l∈NC（p）.

Next proposition shows that,when Ci→C,the limit of normal cones of Ciat some special points keeps a fixed relation to some tangent directions.

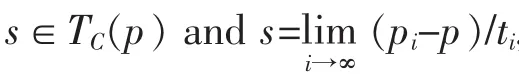
The third one shows that a sequence “close to” an s-attaining sequence is also an s-attaining sequence.

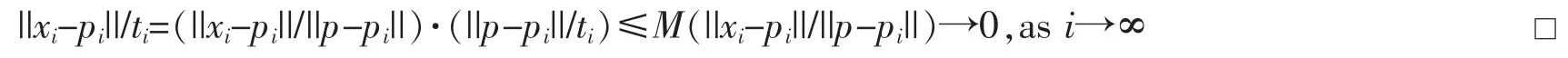
3 The proof of main theorem

The key step in the proof of Theorem C is to construct,by “cutting off” the given reduced body,a sequence of convex bodies whose width directions tend to the direction we hoped.Here we present such a kind of construction.

Given a convex body C and p∈bdC.For 0＜r＜max{｜y－p｜｜y∈C},we denote C1=conv（CB）,where B：={z|||z－p||＜r},and then define

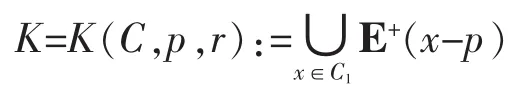
where E+（x-p）：={t（x-p）｜t≥0}.Now,we construct a convex bodyby “cutting off” C as following

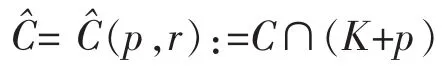
Proposition 6Each K defined as above is a closed convex cone.

Now we show that K is convex.If x1，x2∈K,then x1=λ1（x1′-p），x2=λ2（x2′-p）,for some x1′，x2′∈C1and λ1，λ2≥0.If at least one of x1and x2is zero,then for any α∈[0，1],αx1+（1-α）x2∈K is clear.So we may assume that both x1and x2are not zero（so λ1，λ2＞0）.Thus,for any α∈[0，1],

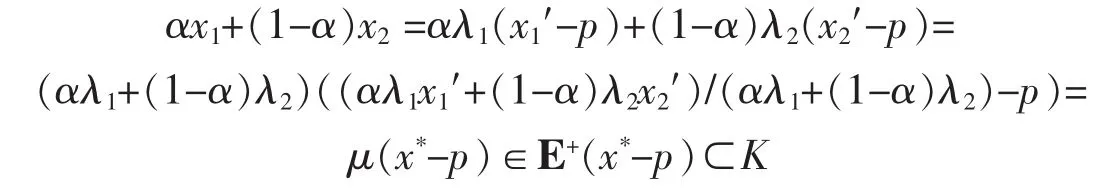
where μ=αλ1+（1-α）λ2＞0,x*=（αλ1x1′+（1-α）λ2x2′）/（αλ1+（1-α）λ2）∈C1since C1is convex. □

Corollary 1Eachdefined as above is a convex body.

Proof.By Proposition 6 and the definition of,is clearly compact and convex.By the construction of C1,we see intC1≠Ø and so int≠Ø,where “int” denotes the interior.Sois a convex body. □

In order to prove Theorem C,more lemmas are needed.

Lemma 1For a convex body C,the boundary of each convex body（p，r） constructed as above contains segments with p as an endpoint.

Proof.Choose q∈bd∩bdC,where：={z|||z-p||≤r}and “bd” denotes the boundary,then q≠p clearly.Now[p，q]∈since p，q are in both C and K+p.Obviously q∈bd（K+p）,so by Theorem 1.3.9 in[10]there is a support hyperplane H of K+p such that[p，q]⊂（K+p）∩H which implies[p，q]⊂bd（K+p） and further[p，q]⊂bdC^. □

Lemma 2If a convex body C is strictly convex,then for any p∈bdC and any applicable r＞0,（p，r）⊆C properly.

Proof.It is obvious since（p，r） contains always segments on its boundary. □

Now it is the time to prove Theorem C.

Proof of theorem C.Suppose p∈bdR and l∈extrNR（p）（without loss of generality,we assume l∈Sn-1）.Then there is a support hyperplane（of NR（p） at l） H：={z∈En｜〈s，z〉=0}（0≠s∈En）,such that

Observing s∈TR（p）,we have a sequence{pi}⊂R and a sequence{ti}⊂E such that ti↓0 and（pi-p）/ti→s as i→∞.We may clearly assume that all piare distinct from p.

Now,set ri：=（1/i）｜pi-p｜and define Ri：=（pi，ri），i=1，2，….By Lemma 2,Ri⊆R properly,so Δ（Ri）＜Δ（R）for all i.Let li∈Sn-1be a width direction of Riand[pi′，pi″]be a chord as mentioned in Proposition 2,then one of pi′，pi″,say pi′,must satisfy ｜pi′-pi｜≤rifor otherwise we would have NR（pi′）=NRi（pi′），NR（pi″）=NRi（pi″） and further Δ（R）≤w（R，li）=｜pi′-pi″｜=Δ（Ri）.Without loss of generality,we may assume li∈NRi（pi′）（otherwise we consider-li）.

Finally,with the help of Proposition 1 we have

which leads to w（R，l）=Δ（R）,i.e.l is a width direction.

RemarkIf p∈bdB is regular,then NR（p） is just a ray,so Theorem C recovers Dekster's result in the case where R is a strictly convex reduced body.

[1]HEIL E.Kleinste konvexe Körper gegebener Dicke[R].Darmstadt：Fachbereich Mathematik der TH Darmstadt，1978.

[2]LASSAK M，MARTINI H.Reduced convex bodies in Euclidean space-A survey[J].Expositiones Math，2011,29：204-219.

[3]DEKSTER B V.Reduced strictly convex plane figure is of constant width[J].J Geom，1986，26：77-81.

[4]LASSAK M.Approximation of bodies of constant width and reduced bodies in a normed plane[J].J Convex Anal，2012，19：865-874.

[5]LASSAK M，MARTINI H.Reduced convex bodies in finite dimensional normed spaces：A survey[J].Results Math，2014,66：405-426.

[6]LASSAK M，MARTINI H.Reduced bodies in Minkowski space[J].Acta Math Hungar，2005,106：17-26.

[7]LASSAK M.Reduced convex bodies in the plane[J].Israel J Math，1990，70：365-379.

[8]DEKSTER B V.On reduced convex bodies[J].Israel J Math，1986，56：247-256.

[9]SCHNEIDER R.Convex Bodies：The Brunn-Minkowski Theory[M].2th ed.Cambridge：Cambridge University Press,2014.

[10]BARVINOK A.A Course in Convexity，Graduate Studies in Mathematics[M].USA：American Mathematical Society，1963.

责任编辑：谢金春

2016－04－08

国家自然科学基金资助项目（11271282；11671293）；苏州科技学院研究生创新项目（SKCX14＿054）

吴宏建（1989－），男，山东滕州人，硕士研究生，研究方向：凸几何分析。

严格凸简约体的宽度方向

吴宏建，国 起
（苏州科技大学 数理学院，江苏 苏州 215009）

若任何真含于其内的凸体的宽度严格小于其宽度，由此凸体称为简约体。现已知严格凸的2维简约体就是等宽体，但相应结论对一般的n维简约体是否成立仍是一个公开问题。为此，该文研究了n维简约体的宽度方向。

严格凸简约体；宽度方向；法锥；端射线

O177；O18MR（2010） Subject Classification52A38

A

2096－3289（2017）04－0009－05

*通信作者：国 起（1957－），男，博士，教授，硕士生导师，E－mail：guoqi@mail.usts.edu.cn。