ABC算法优化SVR的磨损故障预测模型

刘建新，杨庆玲

ABC算法优化SVR的磨损故障预测模型

刘建新1，杨庆玲2

（1.烟台工程职业技术学院，山东 烟台 264001；2.烟台职业学院，山东 烟台 264001）

为了提高故障预测的精度，针对支持向量回归SVR(Support vector machine for regression，SVR)参数选择困难的问题，提出一种采用人工蜂群 (artificial bee colony，ABC)算法优化支持向量回归（SVR）的故障预测模型(ABC-SVR)。该模型先对样本数据进行重构，然后将故障预测误差（适应度）作为优化目标，通过ABC算法寻优找到最优的SVR参数，建立故障预测模型。最后通过实例仿真验证模型的优越性。采用ABC算法优化的SVR故障预测模型进行时间序列预测，能够较好地跟踪发动机滑油金属元素浓度的变化过程，并且能够提前2个取样时间预测异常情况的出现。ABC-SVR模型有效解决了SVR参数选择难题，能够更加准确地表现故障变化规律，提高了故障预测精度。

磨损故障；人工蜂群优化算法；支持向量回归；预测模型

支持向量回归(Support vector machine for regression，SVR)是在统计学习理论的基础上发展起来的一种新的通用学习方法，通过建立线性函数来实现线性回归，用核函数代替线性方程中的线性项来实现非线性回归，适用于对有限样本数据的回归分析，已被广泛用于数据分类、预测等各个领域。在使用SVR进行预测的过程中，它的不敏感损失函数参数、惩罚系数、核函数及其参数等模型参数的选择对预测结果具有很大的影响[1]。目前常用遗传算法、粒子群优化算法等对SVR预测模型的参数进行优化，但这些优化算法在寻优过程中常常不同程度的陷入局部最优，难以达到理想的预测效果[2-3]。人工蜂群算法（Artificial Bee Colony，ABC）是由Karaboga于2005年提出的一种新的基于群智能的全局优化算法。其直观背景来源于蜂群的采蜜行为，蜜蜂根据各自的分工进行不同的活动，并实现蜂群信息的共享和交流，解决了扩展新解域与在已知解域进行精细搜索之间的矛盾，在很大程度上避免了陷入局部最优解问题，从而找到问题的最优解[4-5]。因此，文中提出一种基于支持向量机回归和人工蜂群优化算法的故障预测方法，以提高故障预测的准确性。

1 人工蜂群（ABC）算法描述

人工蜂群(ABC)算法的原理就是模拟实际蜜蜂的采蜜机制。它将人工蜂群分为观察蜂、采蜜蜂和侦察蜂3类，整个蜂群的目标是寻找花蜜量最大的蜜源。采蜜蜂利用先前的蜜源信息寻找新的蜜源并与观察蜂分享蜜源信息；观察蜂在蜂房中等待并依据采蜜蜂分享的信息寻找新的蜜源；侦查蜂的任务是寻找一个新的有价值的蜜源，它们在蜂房附近随机地寻找蜜源。在ABC算法中，食物源（蜜源）的位置用解空间中的点来替代，蜜蜂采蜜（寻找食物源）的过程也就是搜寻最优解的过程。每个蜜源的位置代表问题的一个可行解，蜜源的花蜜量对应于相应的解的适应度，寻找并采集蜜源的速度对应问题求解的速度[6-8]。

假设ABC算法包含个初始解，其中为食物源数目。每个解x=(x1，x2，…，x)为一个维的向量（=1，2，…，，以及为优化参数的个数）。然后，观察蜂、采蜜蜂和侦察蜂开始进行循环搜索，循环次数为MCN。先由观察蜂对相应的食物源（可行解）进行一次邻域搜索，当观察蜂寻找到的食物源（可行解）的花蜜数量（解的适应度）优于之前的，这时就用新的食物源位置（可行解）替代原来的食物源位置，否则食物源位置保持不变。当所有的观察蜂完成搜索之后，观察蜂跳摆尾舞与采蜜蜂共享蜜源信息。采蜜蜂依据得到的蜜源信息在一定的概率条件下选择食物源。花蜜量越大（适应度越优）的食物源（可行解），被选择的概率越大。当采蜜蜂选中食物源后，也要进行一次邻域搜索，然后把它搜索的结果与观察蜂进行比较，当采蜜蜂的搜索解优于观察蜂的解时，此时可行解进行更新，即替换原观察蜂的解，完成角色互换；反之，保留有观察蜂的解。ABC算法求解的过程，就是通过反复搜索可行解来最终找到最优解的过程。

观察蜂和采蜜蜂按照式（1）进行邻域搜索来完成蜜源（食物源）位置的更新[9]：

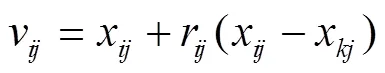
采蜜蜂按照概率p对第个食物源进行选择，当对函数最大值寻优时，p依据式（2）进行确定：

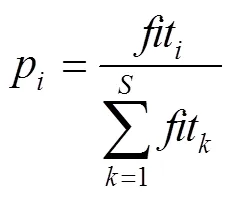
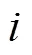
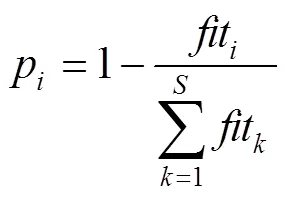
此外，ABC算法中的控制参数limit，表示某个可行解被更新的次数[10]。在寻优过程中，如果某个可行解连续经过limit次循环之后仍然没有被更新，此时这个解陷入了局部最优，与这个解相对应的观察蜂也转变为侦察蜂，这个食物源位置（可行解）就要被放弃。假设被放弃的解是x，则由侦查蜂通过式（4）随机产生一个新的解来代替x。

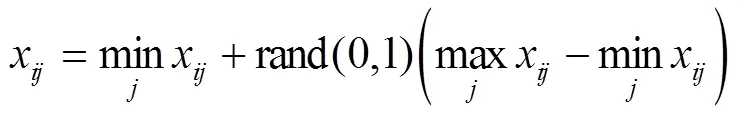
2 ABC算法优化的SVR故障预测模型

根据支持向量机(Support Vector Machine，SVM)的构造原理可知[11-13]，支持向量回归模型（SVR）就是对目标函数求极值，可通过式（5）表示：

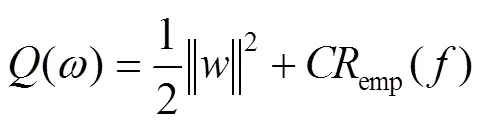
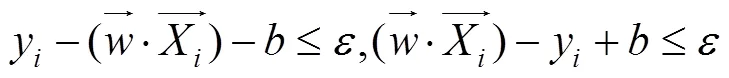
引入Lagrange函数：

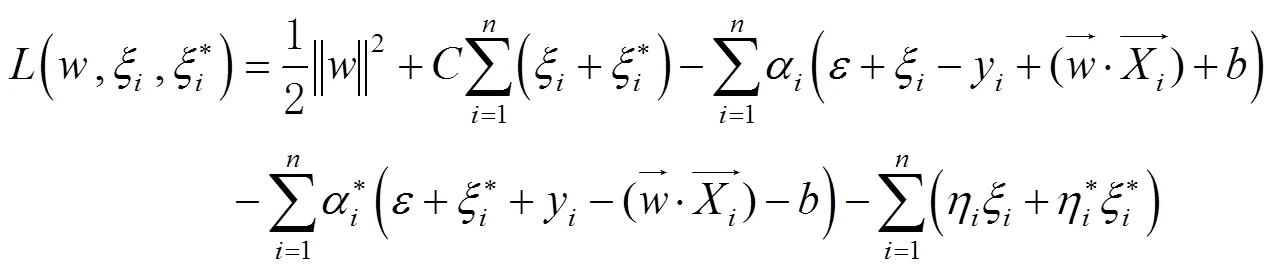
s.t

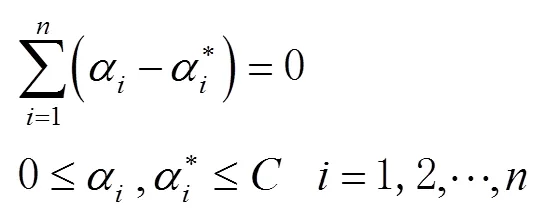
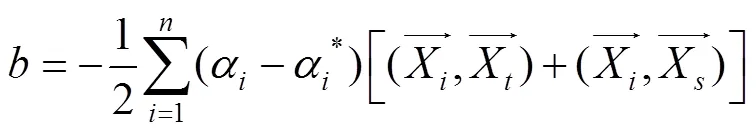
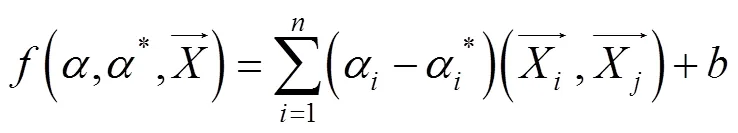
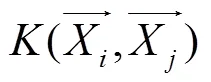
s.t

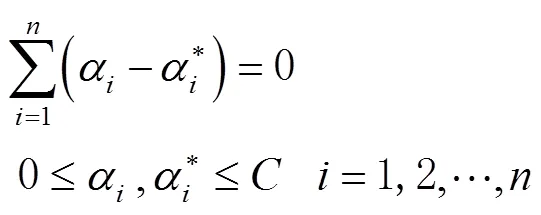
与之对应，回归函数也做相应变化，式（11）可表示为：

通过式（13）就可建立支持向量机的回归模型（SVR）。

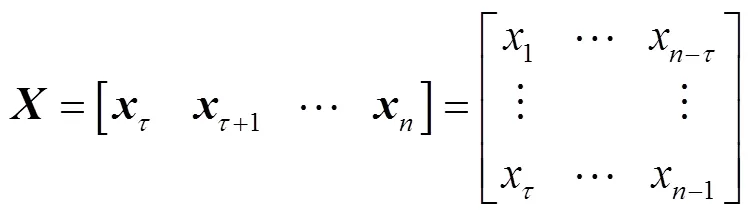
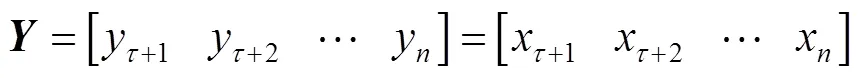
根据式(8)，可建立SVR回归预测模型：

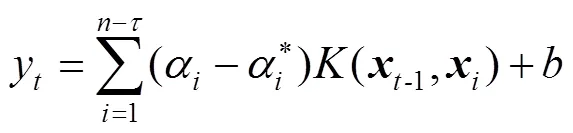
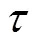
在ABC算法中，蜂群采蜜行为对应着预测问题，见表1。食物源（蜜源）的位置对应预测问题的一个可行解，即预测模型中需要优化选择的参数；食物源的花蜜量大小对应预测模型的预测误差大小；搜寻食物源和采蜜的速度对应参数优化问题的求解速度；当得到最大花蜜量时表示取得了最佳的预测效果，即此时预测误差达到最小。

表1 蜂群采蜜行为与预测问题对应关系

ABC算法中，进行参数优化的依据是适应度，其过程是根据适应度的大小来评判食物源位置（可行解）的优劣[16-17]。进行参数优化的目的是使预测模型的预测总误差达到最小，因此，适应度通常通过预测总误差来表示：

基于人工蜂群优化算法和SVR的预测方法的使用过程可分为以下几个步骤[18-19]。

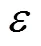
第二步，观察蜂依据式（1）进行领域搜索，当搜索到的食物源的适应度比前面的更优时，则用对食物源位置进行更新，否则保持食物源位置不变。

第三步，求取所有食物源的适应度，并按照式（3）计算发生概率，采蜜蜂依据概率大小选择食物源（可行解），并进行领域搜索，根据食物源的适应度对食物源的位置进行更新，并完成与观察蜂的角色互换。

第四步，在经过limit次循环之后，判断是否存在局部最优解。若存在局部最优解，则侦察蜂根据式（4）对食物源位置进行更新。

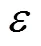
3 实例分析

在进行发动机磨损故障预测时，通常采用监测发动机滑油中金属元素的含量的方式来实现。现对某型航空发动机滑油中金属元素Mg的浓度进行分析，采用光谱分析方法来实现。依据采样时间的先后顺序，将获得的Mg浓度数据进行排列，形成一个Mg浓度时间序列（94个数据点），如图1所示。可以看出，在第94次取样时，Mg的浓度值发生了大幅度升高，据此可以判断该发动机内部发生了异常磨损。现在采用基于ABC算法优化的SVR预测模型对该时间序列进行分析，前60个数据作为训练样本，后34个数据作为测试样本，其预测结果如图2所示。其中，图2b预测残差结果，预测残差表示实测值减去预测值之后的数值。可以看出，在60到90之间取样时，预测误差相对较小，基于ABC算法优化的SVR预测模型能够很好地跟踪正常状态下系统的变化过程。在第92次取样时，预测残差陡然增大，这说明从第92次取样之后发动机内部就进入了磨损异常状态。因此采用ABC算法优化的SVR故障预测模型进行时间序列预测，能够较好地跟踪发动机滑油金属元素浓度的变化过程，并且能够提前2个取样时间预测异常情况的出现（故障的发生）。

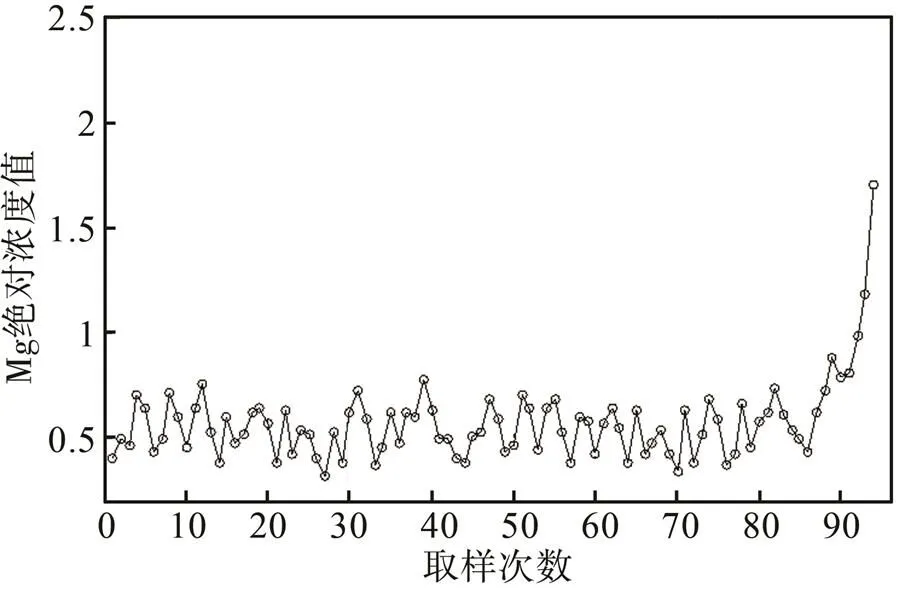
图1 Mg元素浓度的时间序列

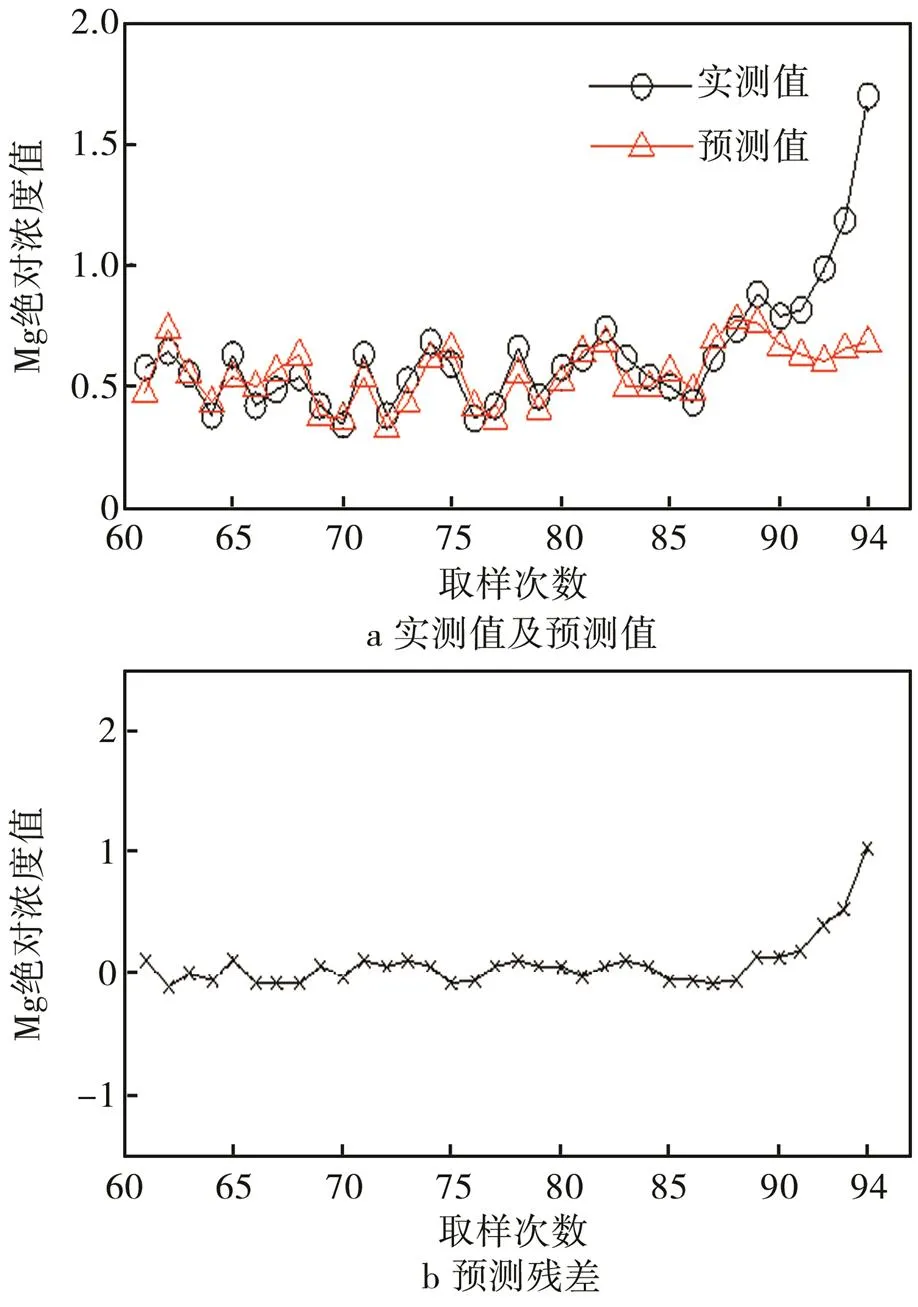
图2 测试数据的预测结果

4 结语

文中利用支持向量回归和人工蜂群算法的优点，提出了ABC-SVR的故障预测模型。结果表明，该方法利用人工蜂群算法能够克服局部最优解，解决了SVR参数选择的难题，能够提前较好的预测故障的发生，具有广泛的应用前景。

[1] FERREIRA J P, CRISOSTOMO M M, COIMBRA A P. SVR Versus Neural-fuzzy Network Controllers for the Sagittal Balance of a Biped Robot[J]. IEEE Transactions on Neural Networks, 2009, 20(12): 1885-1897.

[2] MAO Y, ZHOU X, PI D, et al. Parameters Selection in Gene Selection Using Gaussian Kernel Support Vector Machines by Genetic Algorithm[J]. Journal of Zhejiang University SCI-ENCE, 2005, 68(10): 961-973.

[3] MING GAO, XIA HONG, SHENG CHEN. A Combined SMOTE and PSO Based RBF Classifier for Two-class Imbalanced Problems[J]. Neurocomputing, 2011, 74(17): 3456-3466.

[4] ZHU G, KWONG S. Gbest-guided Artificial Bee Colony Algorithm for Numerical Function Optimization[J]. Applied Mathematics and Computation, 2010, 217(7): 3166- 3173.

[5] OMAKAR S N, SENTHILNATH J, KHANDELWAL R, et al. Artificial Bee Colony(ABC) for Multi-objective Design Optimization of Composite Structure[J]. Applied Soft Computing, 2011, 11(1): 489-499.

[6] KARABOGA D, BASTURK B. On the Performance of Artificial Bee Colony(ABC)Algorithm[J]. Applied Soft Computing, 2008, 8(1): 687-697.

[7] KARABOGA D, AKAY B. A Comparative Study of Artificial Bee Colony Algorithm[J]. Applied Mathematics and Computation, 2009, 214(1): 108-132.

[8] PAN Q K, TASGETIREN M F, SUGANTHAN P N. A Discrete Artificial Bee Colony Algorithm for the Lot- streaming Flow Shop Scheduling Problem[J]. Information Sciences, 2011(181): 2455-2468.

[9] SINGH A. An Artificial Bee Colony Algorithm for the Leaf Constrained Minimum Spanning Tree Problem[J]. Applied Soft Computing, 2008, 9(2): 625-631.

[10] KARABOGA D, BASTURK B. A Powerful and Efficient Algorithm for Numerical Function Optimization: Artificial Bee Colony(ABC)Algorithm[J]. Journal of Global Optimization, 2007, 39(3): 459-471.

[11] KARABOGA D, BASTURK B. A Comparative Study of Artificial Bee Colony Algorithm[J]. Applied Mathematics and Computation, 2009, 214(1): 108-132.

[12] LORENZI L, MERCIER G, MELGANI F. Support Vector Regression with Kernel Combination for Missing Data Reconstruction[J]. IEEE Transactions on Geosciences and Remote Sensing Letters, 2012, 10(2): 367-371.

[13] CAMPS-VALLS G, BRUZZONE L, ROIO-ALAVREZ J L, et al. Robust Support Vector Regression for Biophysical Variable Estimation from Remotely Sensed Images[J]. IEEE Geosci Remote Sens Lett, 2009, 3(3): 339-343.

[14] ELATTAR E E, GOULERMAS J, WU Q H. Electric Load Forecasting Based on Locally Weighted Support Vector Regression[J]. IEEE Transactions on Systems, Man, and Cybernetics, 2010, 40(1): 438-447.

[15] 王坤, 员晓阳, 王力. 基于改进模糊支持向量回归模型的机场能源需求预测[J]. 计算机应用, 2016, 36(5): 1458-1463.

[16] 朱志洁, 张宏伟, 王春明. 基于人工蜂群算法优化支持向量机的采场底板破坏深度预测[J]. 重庆大学学报, 2015, 38(6): 37-43.

[17] 陈健飞, 蒋刚, 杨剑锋. 改进ABC-SVM的参数优化及应用[J]. 机械设计与制造, 2016(1): 24-28.

[18] 施俊, 高正夏, 徐嵚嵛. 基于ABC-SVM的软基沉降预测研究[J]. 河南科学, 2016, 34(5): 741-745.

[19] 高相铭, 杨世凤, 潘三博. 基于EMD和ABC-SVM的光伏并网系统输出功率预测研究[J]. 电力系统保护与控制, 2015, 43(11): 86-92.

Wear Fault Prediction Model Based on SVR Optimized by ABC

LIU Jian-xin, YANG Qing-ling

(1.Yantai Engineering & Technology College, Yantai 264001, China; 2.Yantai Vocational College, Yantai 264001, China)

To improve the prediction accuracy of wear faults, a wear fault prediction model (ABC-SVR), which was based on support vector machine for regression (SVR) optimized by artificial bee colony(ABC) algorithm was proposed.The model reconstructed the time series of wear faults and took the wear fault prediction accuracy as the optimization objective to find out the optimal SVR parameters by ABC algorithm and build prediction model of wear faults. Finally, the simulative contrasting experiment was applied to test the performance of the model.Time series prediction with SVR forecasting model optimized by ABC algorithm could track the concentration change process of metallic element in engine lubricating oil and predict the presence of the abnormal situation ahead of 2 sampling time.ABC-SVR solves the problem of SVR parameter optimization, can describe the complicated change rules of wear faults accurately, and improves the accuracy of wear faults prediction.

wear faults; artificial bee colony optimization algorithm; support vector machine for regression; prediction model

10.7643/ issn.1672-9242.2017.11.020

TJ01

A

1672-9242(2017)11-0098-05

2017-07-04；

2017-08-09

刘建新（1967—），山东烟台人，硕士，副教授，主要研究方向为机械设计与制造。