探索格雷码的奥秘
2017-11-24韩宏峰,吴佳耕,张亦之,袁健华
韩宏峰,吴佳耕,张亦之,袁健华


摘要:本文创作的目的是针对本科生在数字电路设计课程中初步接触格雷码感到困惑,并不知道如何快速书写格雷码或如何与其他数制转换的情况下,提出的以多种方式快速获取格雷码的方法。
关键词:格雷码;数制转化;卡诺图;逻辑代数
中图分类号:G642.0 文献标志码:A 文章编号:1674-9324(2017)47-0160-03
正如多数教科书所述,首先列出格雷码和对应二进制的转换表格,简单说明格雷码“每次只变一位”的稳定特性。下图是典型的二进制格雷码和其他数码的转换。
请看第二列自然二进制码从第四行(0011)变到第五行(0100)时,电位变化了3位。我们知道,数字电路中多位数码同时发生变化是不可能的,所以变化过程中不可避免地出现“粗大错误”:即0011可能先变为0111,然后逐渐变回0100。格雷码因为相邻数字只变化一位从而解决了“粗大错误”的问题。然而,教科书往往没有提供具体实用的公式来获得格雷码。基于这种情况,本文的作者进行了深入研究,总结并提出了三种具体获取格雷码的方式,使初学者能够简单正确地获取格雷码。同时,作者通过JAVA编程语言实现这一转换过程[核心代码参见III]并提供了GUI,拥有更好的用户交互体验,可以将任意非负整数转换成格雷码。本文的研究是结合概念分析(卡诺图的原理和基本门电路的计算)和编程实现。
对于数字电路的初学者,常常接触诸如二,八,十六进制,格雷码等数字系统和转化。每种编码都有优点和适用范围。除格雷码外,大部分的进制转换规则相似,所以初学者往往对格雷码感到陌生,不能快速准确处理格雷码。所以本文总结了三种方法准确快速获取格雷码。
一、图形观察法:基于卡诺图原理
对于n变量代数,我们通过卡诺图得以简化。下面以四变量卡诺图为例。(表格1)
通常,我们学习卡诺图仅仅是为了进一步地简化操作。但实际上它为我们提供了更多的信息。如果尝试从0000按照S型顺序:
0000-0001-0011-0010-0110-0111-0101-0100-1100-1101-1111-1110-1010-1011-1001-1000的方向,所得到的结果序列就是对应的十进制数字0—15。
这种方法的提出是基于概念的支持。由于格雷码是使错误最小化的转换,相邻值仅改变1位,因此该方法从该设计理念中受益。所以这是获取格雷码的最简便的方法。优点是无须掌握额外的技能,只需要掌握卡诺图的书写技能。
当我们尝试将卡诺图拓展到五变量的时候,会发现虽然画卡诺图效率较低,但依然可以得出正确的与卡诺图对应的十进制数字。(表格2)
这次我们效仿上述方法,直接将十进制数字按照S型填入卡诺图,我们便可以直接获得格雷码和十进制数字的转化关系。比如:格雷码“01000”对应十进制的15,十进制的“22”对应格雷码“11101”。
然而,绘制卡诺图的过程降低了有效性。因此本文提供了第二种方法。
二、逻辑代数:通过应用异或门电路
方法一给出的策略是简单的,但随着位数的增加效率会降低。因此掌握代数运算是至关重要的。
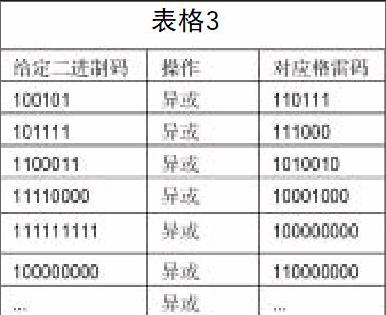
规定如下:(表格3)
Bi=Gi?茌Bi+1(n-1≥i≥0)
(G:格雷码 B:二进制码)
采取如下规则:给定随机二进制码,第一位数字保持相同,通过异或运算将第二位与第一位进行比较,为真则第二位标记1,否则标记0。同理比较第三位和第二位,直到最后一位。简言之,我们将第(i+1)位与第i位进行比较,如果它们相同,则标记为0,如果不同则标记为1。通过此方法我们可以简单又快速地由任意二进制数快速获取对应的格雷码。
现如今随着计算机科学的发展,计算机逐步融入人们的生活,所以本文作者基于上述异或门电路原理通过JAVA GUI进行了开发。
三、基于Java编程语言开发的GUI界面
由于JAVA具有友好的交互界面和通用性的特点,因此采用了JAVA来实现编程。在图形界面中,用户可以通过键盘任意输入一个十进制数的非负整数然后点击转换按钮,界面将直接呈现出对应的格雷码。
核心算法如下:
四、结论
本文总结出三种二进制码和格雷码的转换方式,读者可根据自己的理解选择最适合自己的方法。第一种方法提供了准确的解法,第二种方法最高效,而最后的JAVA图形界面是最实用的。希望这项研究能为初学者深入了解格雷码打下坚实基础。
参考文献:
[1]John F.Wakerly,[Digital Design:Principles and Practices],Fourth-Edition,Pearson-Education.Inc,China Machine Press,2007.
[2]M.Morris Mano and Michael D.Ciletti,[Digital Design],Fourth Edition,Pearson-Education.Inc,Publishing House of Electronics Industry.
[3]胡福云.巧用卡諾图记忆格雷码[J].电子制作,2013,(13).
[4]胡锦.数字电路与逻辑设计[M].北京:高等教育出版,2005.
