一类推广的非单调拟牛顿算法

徐莹莹,陈 阳

(郑州工业应用技术学院基础教学部，河南 郑州 451150)

一类推广的非单调拟牛顿算法

徐莹莹,陈 阳

(郑州工业应用技术学院基础教学部，河南 郑州 451150)

目的为了更有效地利用拟牛顿算法求解无约束优化问题,提高拟牛顿算法的收敛速度，并在数值实验上得到最优解。方法针对拟牛顿方程进行修正，在修正的拟牛顿方程基础上添加参数，利用修正BFGS校正公式,采用非单调线性搜索准则，提出一类新的非单调拟牛顿算法。结果新算法推广了已有的拟牛顿方程，在一定条件下，具有全局收敛性,利用Matlab编制程序对新算法进行数值实验。结论通过数值试验，选取测试函数，得到了最优解。证明了推广的非单调拟牛顿算法是有效的。利用新算法可以更有效地求解无约束优化问题。

无约束优化；非单调；拟牛顿方程；线性搜索；全局收敛性

本文基于Z.X.Wei[6],W.Xiao,F.J.Sun[7]提出的修正的拟牛顿方程，利用修正的BFGS校正公式[8]，结合非单调线性搜索准则[9]，提出了一类新的非单调拟牛顿算法，并根据文献[8]的证明思路,证明了新的非单调拟牛顿算法具有全局收敛性[10]。

1 算 法

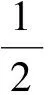
(1)

并给出了矩阵的3种选择：

(2)

其中γk=2(fk-fk+1)+(gk+gk+1)Tsk。

(3)

其中γk=2(fk-fk+1)+(gk+gk+1)Tsk。

通过以上分析，本文提出的算法步骤如下：

Step1 给出初始点x0∈Rn和初始正定矩阵B0∈Rn×n，令k∶=0;

Step2 若‖gk‖=0则停止，否则计算Bkdk=-gk得到搜索方向dk;

Step3 利用非单调线性搜索[9]得到步长αk。

(4)

(5)

利用xk+1=xk+αkdk得到下一个迭代点。

Step4 令sk=xk+1-xk,如果‖xk+1-xk‖=0，则停止;否则计算

(6)

其中ε充分小。利用文献[8]中改进的BFGS校正公式

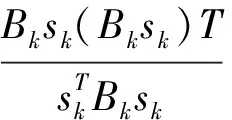
(7)

得到对称正定矩阵Bk+1。

Step5 令k=k+1，转第二步。

2 收敛性分析

做如下假设：

假设(1)：水平集Ω={x|f(x)≤f(x0)}包含于一个有界凸集D上；

假设(2)：目标函数f(x)是一致凸的，即存在正常数c1,c2， 使得c1‖z‖2≤zTG(x)z≤c2‖z‖2,∀x,z∈Rn;

假设(3)：目标函数f(x)是二阶连续可微的。

(8)

其中ε=xk+θsk,ε3=xk+θ1ksk,ε4=xk+θ2ksk,θ、θ1k、θ2k∈(0,1)。

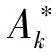
(10)

证明

(11)

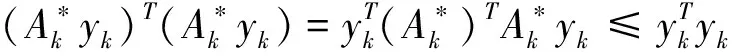
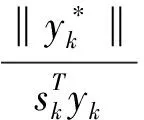
引理4[7]若假设(3)成立，则存在ε0(ε0gt;0)满足

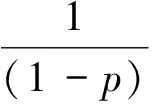
(12)

定理2 若假设(1)、(2)、(3)成立，如果x0是初始点，B0是任意对称正定矩阵，且序列{xk}由算法产生，其中步长αk由非单调线搜索决定。则lim inf‖gk‖=0。

证明根据引理4和(5)式可得

f(xk+1)≤f(xh(k))-ε1‖sk‖rk

根据引理6可得

(13)

由于xk∈Ω,Ω是有界的，则存在cngt;0，满足‖gk‖≤cn。故

(14)

下面用反证法来证明。假设lim inf‖gk‖gt;0，即假设存在常数c′gt;0，使得

‖gk‖≥c′,k=0,1,…

(15)

(16)

因此lim inf‖gk‖=0。

3 数值实验

为检验新算法的实验效果，选取文献[15]中的部分测试函数，利用Matlab编制程序对新算法进行了数值实验，新算法中参数设置同文献[7]。k表示迭代次数，依次为：文献[7]中Ak5、文献[6]中Ak2和新算法。fk表示测试函数最优解。

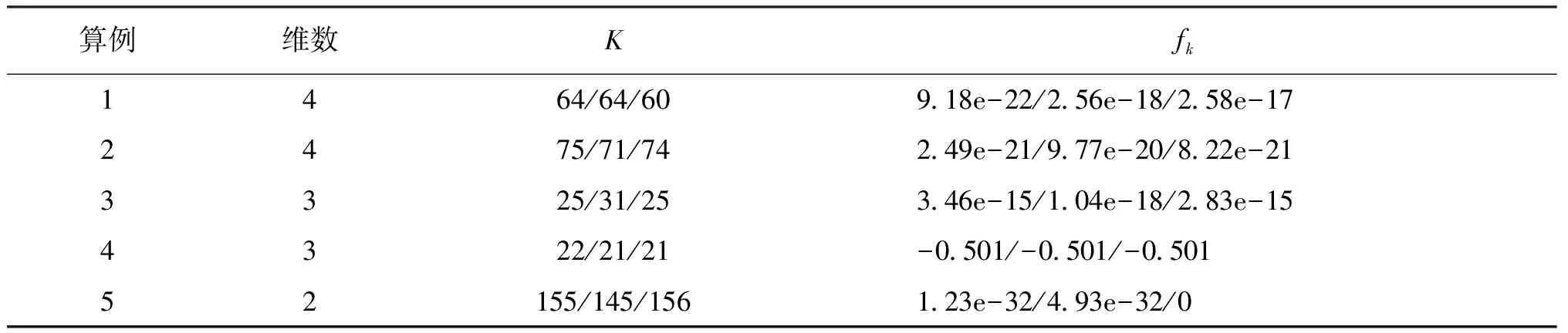
算例维数Kfk1464/64/60918e-22/256e-18/258e-172475/71/74249e-21/977e-20/822e-213325/31/25346e-15/104e-18/283e-154322/21/21-0501/-0501/-050152155/145/156123e-32/493e-32/0

数值实验结果表明本文提出的算法是有效的，并且新算法相对文献中算法的数值实验效果有所改善。

[1] 袁亚湘，孙文瑜.最优化理论与方法[M].北京：科学出版社，1997：183-218.

[2] 刘光辉,尹红婷.BFGS算法的全局收敛性分析[J].曲阜师范大学学报,1994(01):1-8.

[3] 李文钰.一类求解无约束优化的自适应拟牛顿型信赖域算法[J].北华大学学报,2014(06):715-717.

[4] WEI Z X．Convergence properties of class of quasi-Newton algorithm[J].Guangxi Sci,2006(13)：282-287.

[5] 牛潇萌.非线性互补问题光滑化拟牛顿算法[J].计算机工程与应用,2013(18):33-35.

[6] WEI Z X,LI GUO Y,QI L Q.New quasi-Newton methods for unconstrained optimization problems[J].Appl Math Comp,2006:1156-1188.

[7] XIAO W，SUN F J．On quasi-Newton methods with modified quasi-Newton equation[C]//Jiang Yong,Li Jianliang Information Science and Engineering.Proceeding of 2008 International Pre-Olympic Congress on Computer Science.World Academic Press,2008:359-363.

[8] 张华军,赵金,罗慧.基于拟牛顿法的同时扰动随机逼近算法[J].华中科技大学学报,2014(09):1-3.

[9] SUN W Y,Zhou QunYan.An unconstrained method using non-monotone second-order Goldstein’s line search[J].Sci China Series A Math,2007(10):1389-1400.

[10] 易君君,汪宝,颜倩倩.基于新拟牛顿方程的优化算法设计及应用[J].宁波工程学院学报,2015(03):12-18.

[11] YUAN G L，WEI Z X．The superlinear convergence analysis of a non-monotone BFGS algorithm on convex objectivefunctions[J].Acta Math Sinica Engl Series,2008(01):35-42.

[12] 鲍莹莹,王希芸,程翠梨.一种基于弱拟牛顿方程的对角拟牛顿法[J].宁夏师范学院学报,2013(03):15-19.

[13] 王海滨.改进的BFGS算法在一种新搜索下的收敛性[J].河北理工学院学报,2006(02):103-106.

[14] MORE J J,GARBOW BS,HILLSTROM KE.Testing unconstrained optimization software[J].ACM Trans Math Softw,1981(07):17-41.

[15] 孙清滢,徐琳琳,刘丽敏，等.基于稀疏对角拟牛顿方向的非单调超记忆梯度算法[J].工程数学学报,2012(03):375-383.

[责任编辑：刘志媛英文编辑：刘彦哲]

AGeneralizedNon-monotoneQuasi-NewtonAlgorithm

XUYing-ying,CHENYang

(Zhengzhou University of Industrial Technology,Zhengzhou,Henan 451150,China)

ObjectiveTo make the quasi-Newton method suitable for solving the non-constrained optimization problems,and improve the convergence speed of this method and get the optimal solution in the numerical experiment.MethodsBased on modified quasi-Newton equation with parameters and the BFGS updated,using non-monotone linear search criteria,a new quasi-Newton method with non-monotone is proposed.ResultsThe new algorithm,which has popularized the quasi-Newton method,is verified by numerical experiments programmed in the Matlab language and has global convergence under certain conditions.ConclusionsBy giving suitable test functions,global optimal solution is found.And it is demonstrated that this approach effectively solves some problems with unconstrained optimization.

unconstrained optimization；non-monotone；quasi-Newton equation；linear search；global convergence

来稿日期：2016-12-14

徐莹莹(1988-)，女，河南焦作人，郑州工业应用技术学院基础教学部教师，硕士研究生，研究方向为最优化理论与算法。

O 224

A

10.3969/j.issn.1673-1492.2017.11.003